上围子直流接地极对周边直流偏磁的影响

拾　杨，杨茹珊，夏良宇，王沐雪，唐红涛，黄　浩

(1. 国网经济技术研究院有限公司，北京 102209；2. 三峡大学 电气与新能源学院，湖北 宜昌 443002)

0　引　言

当直流输电系统在以单极运行方式下时，大地成为直流输电系统回路的一部分，通过接地极向大地散流[1-3]。由于接地极周边不同位置的变电站存在电位差，且变电站及电厂主变高压侧一般中性点直接接地[4-5]。所以，直流电流会由变压器的中性点流入，流入中性点的直流电流会导致变压器铁芯磁化，从而使变压器的磁化曲线产生偏移，使铁芯饱和，引起直流偏磁。从而产生大量谐波，变压器损耗增加、温升增加、局部过热，变压器噪声增大、振动加剧，无功损耗增大、系统电压下降，继电保护系统不正常运行等问题[6-7]。

精确计算接地极周边的偏磁电流情况，以及对电力系统带来的影响，是直流输电工程中不可缺少的一环。本文以上围子接地极为例对其周边的电力系统进行偏磁电流计算，研究变压器主变的直流偏磁情况，为接地极周边的直流偏磁分布提供了一种参考依据。

1　上围子接地极周边电力系统分布

上围子接地极周边电网结构如图1所示，本文选取极址周围130 km范围内的变电站、电厂及与其有直接电气联系的变电站及电厂。该范围内一共有24座500 kV的变电站及电厂，84座220 kV的变电站及电厂，以及27条为500 kV线路，118为220 kV线路。

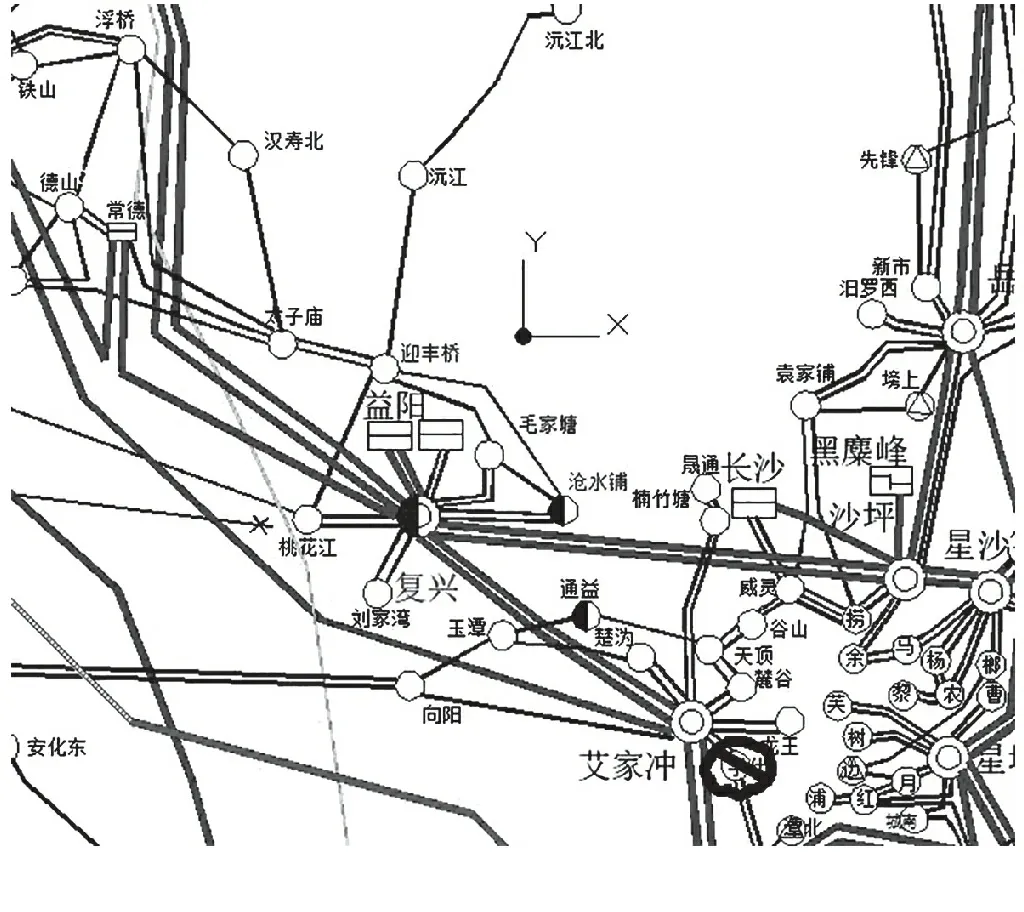
图1　上围子接地极周边电网结构分布图

利用四极法及MT法对上围子接地极周边的土壤电阻率进行测量，从而得到上围子极址大地电性分层及各层等效电阻率，如表1所示。

2　仿真计算原理

图2所示为直流接地极入地电流通过大地散流后流进周边交流电网的示意图。极址的入地直流电流会抬升接地极附近的变电站及电厂所在地区的地表电位。同时，受变电站地理位置不同以及大地土壤电阻率差异，各变电站及电厂地表电位抬升的幅值各不相同，各站出现电位差，从而导致直流电流由大地流入(流出)交流电网。

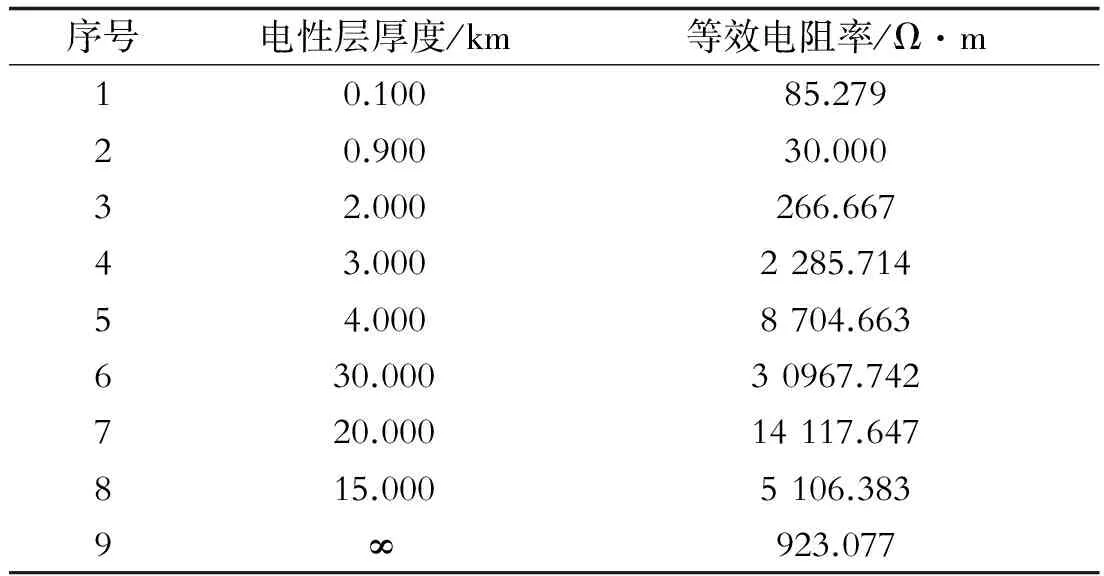
表1　上围子极址大地电性分层

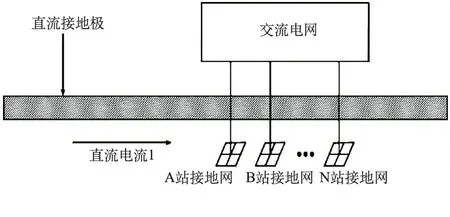
图2　直流接地极电流进入交流电网示意图

为计算流入(流出)各电压器中性点的偏磁电流，可以依据极址周边的地理接线方式及各电力参数得到电力系统直流等值网络模型。

计算原理如下：以m个变电站及n条线路为例，为简化计算，本文将变压器等值直流电阻和变电站的接地电阻简化为一条支路，将输电线路作为另一条支路，简化之后的计算模型中含有2m个节点以及m+n条支路，由此可得节点电压方程

I=YU

(1)

式中，Y为节点导纳矩阵(2m×m)；U为节点电压列向量(2m×1)；I为注入网络节点的列向量(2m×1)。

从等值网络模型中可看出，式(1)中含有m个接地节点和m个非接地节点，所以用a和b分别表示接地节点和非接地节点，同时由于接地节点注入电流为Ia，非接地节点的注入电流为0，所以

(2)

式中，Ya为矩阵(m×2m)；Yb为矩阵(2m×2m)。分列可得：

YaU=Ia

(3)

YbU=0

(4)

由式(4)得：

(5)

式中，Yba为(2m×m)向量；Ybb为(2m×2m)向量。

将式(5)展开得：

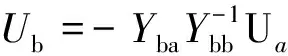
(6)

各站地表电位由大地电流场计算得到，即已知Ua，由式(6)计算可得Ub。

联立式(3)和(6)，计算可得流入各站的偏磁直流为：

(7)

3　上围子接地极周边偏磁电流仿真计算

当强大的直流电流通过接地极散流时，电流通过大地土壤流向远方，由于土壤电性结构复杂，使得在大地表面产生电位差异，但在无穷远处，电位几乎为零。所以，为了更加真实的反映接地极对广域范围内的电力设施产生的影响，本文采用有限元软件对该极址区域1 000 km范围内进行三维土壤建模，由于各站到极址的距离远大于极环半径，故可以等效为点电源注入，注入电流为5 000 A。各站的地表电位由各站点的地理坐标确定。

以两个变电站为例，图3所示为交流电网中两个变电站中性点接地主变之间流通的直流网络模型。其中包含接地电阻、主变电阻和线路电阻。其计算参数以各站实际值为准。

图3　接地主变之间的直流网络模型

极址广域范围内的变电站及电厂220 kV主变为非自耦变压器，500 kV为自耦变压器。其中非自耦变压器高压绕组与低压绕组间没有直流通路，故计算偏磁电流时只需要考虑与输电线路连接的高压绕组，其计算模型如图4(a)所示。而自耦变压器的高压绕组为公共绕组和串联绕组组成，其中中压绕组为公共绕组，其计算模型如图4(b)所示。故计算时需考虑接地极周边各站主变变压器的类型，从而精确计算偏磁电流。

图4　变压器直流模型

接地极周边直流网络模型中输电线路的模型为线路直流电阻值，在高压输电线路中一般采取分裂导线，因此在搭建直流电路时一相直流电阻值为单根导线电阻值除以分裂数，如果含有多回线路并联，再除以线路回数，从而得到线路的直流电阻值。

本文参照2017年上围子周边电网结构分布图建立上围子接地极周边电力系统网络模型，对上围子接地极采用单极大地运行方式时接地极周边变电站直流电流分布进行仿真计算，其部分结果如表2所示。

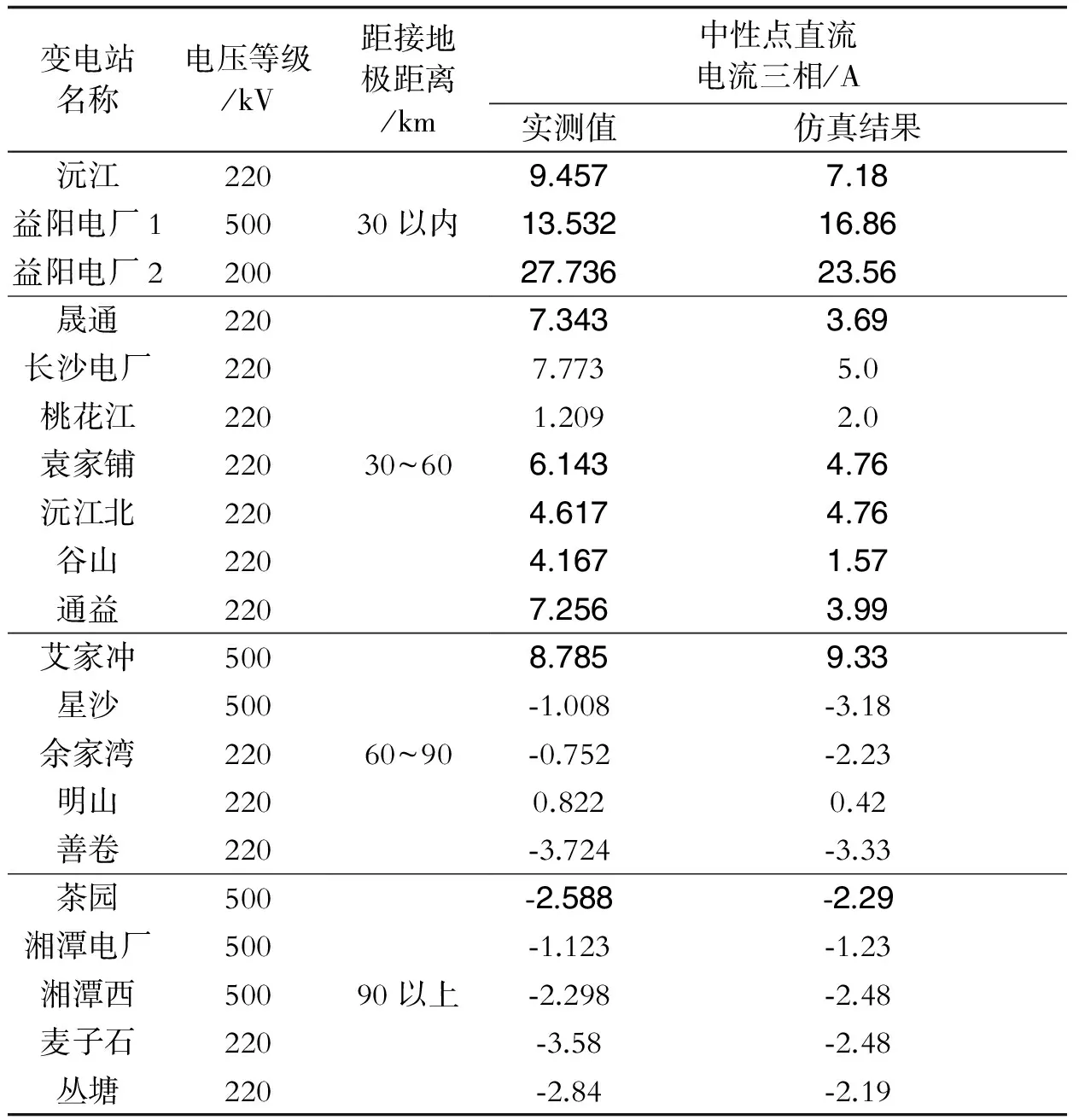
表2　上围子周边变压器中性点直流电流分布

注：加粗为偏磁电流超标。

由表2的数据可知：

(1)从仿真值与实测值的对比结果来看，直流偏磁变化基本一致，且变压器发生直流偏磁的主变主要集中于距离接地极较近的区域。

(2)实测值与仿真电流正负基本保持一致，表明偏磁电流流向与实测相吻合。仿真结果与实测值大体上比较接近，能基本反映流入(流出)各站的偏磁电流大小。

(3)随着各站与接地极距离的增加，电流的变化趋势是逐渐由正变为有正有负到基本全为负，这主要是由于距离接地极较近的变电站电位高，电流从大地流入地电力系统，距离接地极较远的变电站电位低，电流从系统流向大地，而处在中间位置的变电站电流方向有可能为正，也有可能为负，受地电位升的变化比较敏感。

4　结束语

本文通过对上围子接地极周边变电站及电厂主变直流偏磁电流进行仿真计算，得到以下结论：

(1)在对接地极周边主变进行偏磁电流计算时，电网结构、变电站相对位置、变压器类型、输电线路参数、土壤电阻率等都需要考虑，以保证其计算的精确度；

(2)变电站及电厂距离接地极越近，主变发生直流偏磁超标越多，所以接地极周边不宜建立变电站；

(3)各站受地表电位的影响，电流的变化趋势逐渐由正(流入)变为有正有负到基本全为负(流出)；

(4)本文计算结果的准确性，能为接地极周边变压器直流偏磁评估提供有效指导。

参考文献：

[1]曾连生. 直流输电接地极电流对电力变压器的影响[J]. 高电压技术, 2005, 31(4): 57-58.

[2]苑舜, 王天施. 电力变压器直流偏磁研究综述[J]. 高压电器, 2010, 46(3): 83-87.

[3]郭满生, 梅桂华, 刘东升. 直流偏磁条件下电力变压器铁心BH曲线及非对称励磁电流[J]. 电工技术学报, 2009, 24(5): 46-51.

[4]鲁海亮, 文习山, 蓝磊, 等. 变压器直流偏磁对无功补偿电容器的影响[J]. 高电压技术, 2010, 36(5): 1124-1130.

[5]刘同同, 刘连光. 变压器直流偏磁谐波对并联电容器的影响分析[J]. 现代电力, 2012, 29(1): 29-32.

[6]侯永亮. 高压直流输电过程中变压器直流偏磁现象的研究[D]. 保定：华北电力大学硕士毕业论文, 2006.

[7]杨永明, 刘行谋, 陈涛.特高压直流输电接地极附近的土壤结构对变压器直流偏磁的影响[J]. 电网技术, 2012, 36(7): 26-32.