钢结构用自锁式单向螺栓抗拉刚度分析模型
李国强,张杰华
(1. 同济大学土木工程防灾国家重点实验室,上海 200092; 2. 同济大学建筑工程系,上海 200092)
0 引 言
单向螺栓是指连接使用时仅需从被紧固板材一侧进行紧固的螺栓,用于封闭截面连接等不易同时触及连接件两侧的构件连接。
目前,国外有多种不同的单向螺栓产品,例如英国Lindapter International公司的Hollo-Bolt以及根据Hollo-Bolt改进而成的RMH螺栓[1-3]和EHB螺栓[4-5]、英国Advanced Bolting Solutions公司的Molabolt螺栓、英国Blind Bolt公司的Blind Bolt螺栓、美国LNA Solutions公司的BoxBolt,Huck International公司的BOM,HSBB[6]和Ultra-Twist螺栓、澳大利亚Ajax Engineered Fasteners公司的ONESIDE Fastener螺栓、荷兰Flowdrill B V公司的Flowdrill[7]技术等。然而,中国以前没有成熟的单向螺栓产品。
国内外学者对于单向螺栓产品以及单向螺栓连接节点进行了研究[8-17],但主要侧重于单向螺栓的承载力性能,对于单向螺栓抗拉刚度还没有提出比较完善的理论模型。本文根据自锁式单向螺栓研制开发时完成的轴向拉伸试验结果,进一步研究了自锁式单向螺栓的初始抗拉刚度,结合理论计算结果和试验结果提出了单向螺栓初始抗拉刚度分析模型。本文中研究的单向螺栓抗拉刚度为单向螺栓本身的抗拉刚度,即单向螺栓在预拉力消失后的抗拉刚度,而预拉力消失以前的单向螺栓抗拉刚度包含钢板的刚度。
1 单向螺栓简介
钢结构用自锁式单向螺栓可以方便地用于封闭截面构件的连接,如图1所示。安装时把单向螺栓穿入连接板件,使钢垫圈与连接板贴紧(橡胶垫圈需进入螺栓孔内);然后,使用扳手固定住钢垫圈,同时,使用扭矩扳手或电动扳手拧紧螺栓头,此时,由于锥头已经被套筒锁住,螺杆和锥头间发生相对转动,锥头不断向螺栓头方向移动,进而使套筒撑开,套筒撑开的四肢卡住连接钢板;拧紧螺栓头至安装扭矩,安装完成。图2为钢结构用自锁式单向螺栓安装前后示意。

图1 钢结构用自锁式单向螺栓安装示意Fig.1 Schematic Diagram for Installation of Self-lock One-side Bolt for Steel Structure
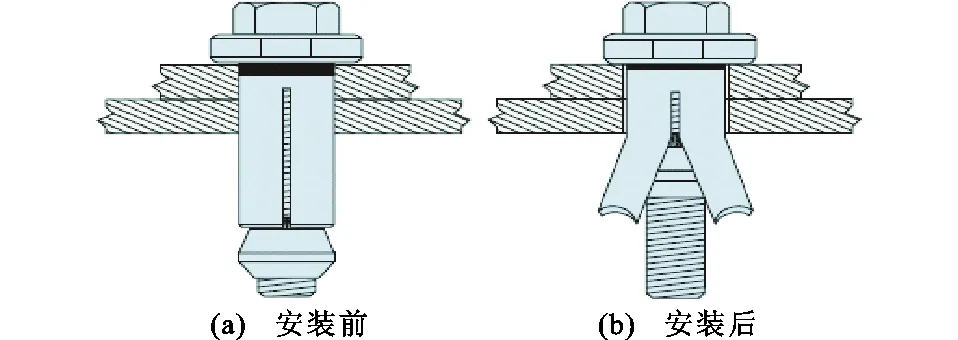
图2 钢结构用自锁式单向螺栓安装前后示意Fig.2 Schematic Diagram of Self-lock One-side Bolt for Steel Structure Before and After Installation
本文研究采用的是由同济大学研制开发的钢结构用自锁式单向螺栓STUCK-BOM[18],该螺栓包括锥头、套筒、橡胶垫圈、钢垫圈、标准螺杆5个部件,按图3所示顺序拼装单向螺栓即可成型。
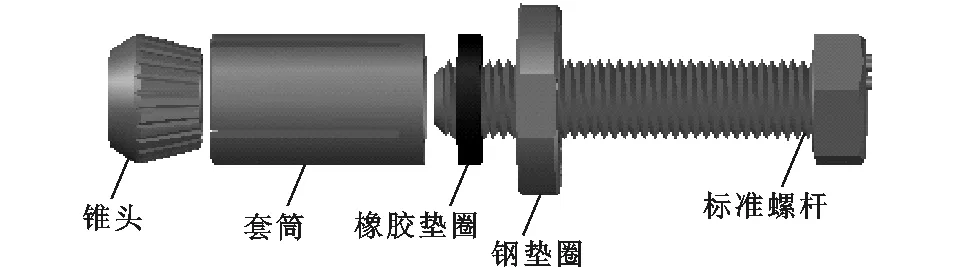
图3 钢结构用自锁式单向螺栓组成部件Fig.3 Components of Self-lock One-side Bolt for Steel Structure
此钢结构用自锁式单向螺栓有8.8级与10.9级2种级别,分别代表螺杆使用标准8.8级和10.9级高强度螺栓全螺纹螺杆,每种强度等级螺栓的型号、尺寸与适用范围如表1所示。

表1 钢结构用自锁式单向螺栓型号、尺寸与适用范围Tab.1 Models, Sizes and Application Scopes of Self-lock One-side Bolts for Steel Structure
2 国产自锁式单向螺栓轴向拉伸试验
2.1 试验方案
试验使用单向螺栓连接2块方形辅助构件,如图4所示,中间连接板厚度h随单向螺栓型号不同(可连接厚度不同)而改变,测量中间连接板随着荷载增加被逐渐拉开的位移。8.8级与10.9级单向螺栓的试验编号、螺栓型号与连接板厚度如表2,3所示,每组试验重复3次。
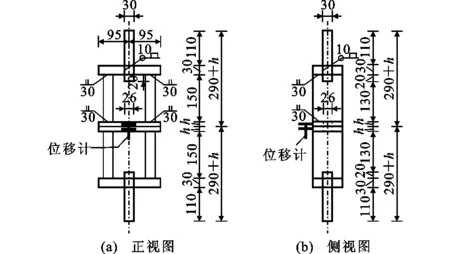
图4 轴向拉伸试验辅助构件(单位:mm)Fig.4 Auxiliary Components of Axial Tensile Test (Unit:mm)
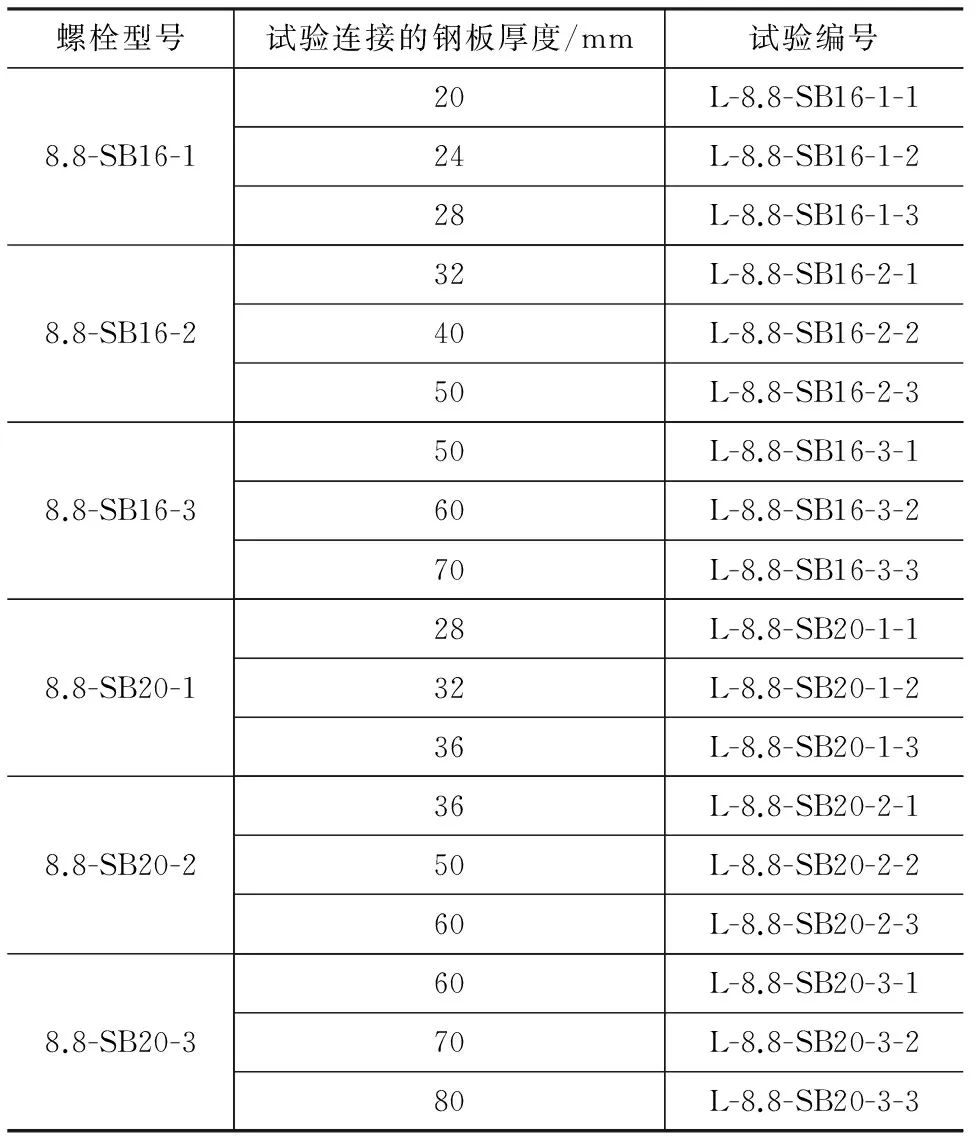
表2 钢结构用国产自锁式8.8级单向螺栓轴向拉伸试验方案Tab.2 Axial Tensile Test Scheme of Domestic Class 8.8 Self-lock One-side Bolt for Steel Structure
2.2 试验结果
钢结构用国产自锁式单向螺栓抗拉承载力较高。单向螺栓在轴向受拉时有2种破坏模式:①单向螺栓从螺栓孔中拔出;②单向螺栓的螺杆被拉断。
单向螺栓受拉时,除螺杆发生拉伸变形外,套筒与螺栓锥头间还可能发生相对滑移,因此抗拉刚度较普通螺栓小。
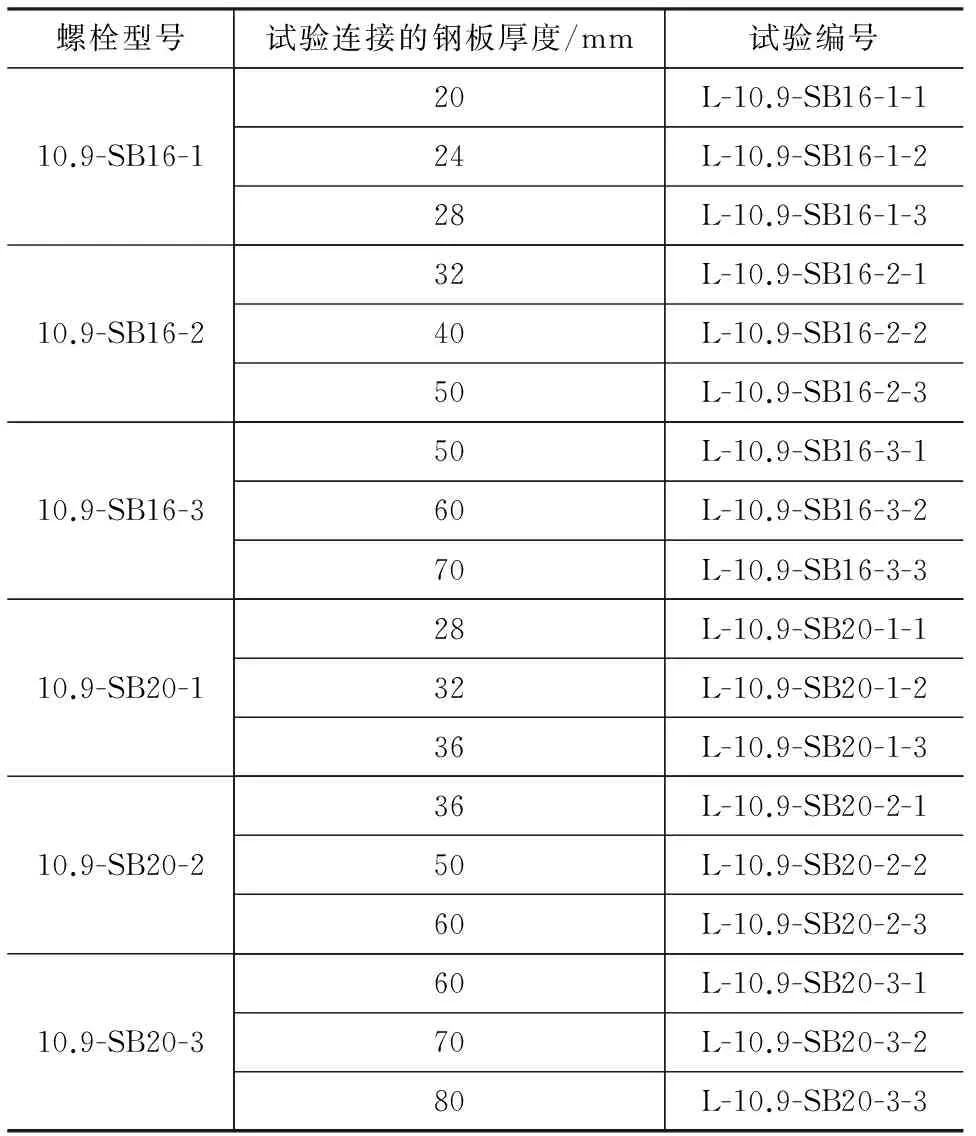
表3 钢结构用国产自锁式10.9级单向螺栓轴向拉伸试验方案Tab.3 Axial Tensile Test Scheme of Domestic Class 10.9 Self-lock One-side Bolt for Steel Structure
由轴向拉伸荷载-位移曲线可得各组单向螺栓初始抗拉刚度的试验值,并用于后文中对单向螺栓初始抗拉刚度理论值进行检验。
3 自锁式单向螺栓拉伸变形(柔度)的组成
图5为自锁式单向螺栓受拉前后的简图。从图5可以看出,自锁式单向螺栓的拉伸变形由三部分组成:①螺杆的拉伸变形;②套筒分肢受到钢板和锥头的挤压发生变形;③在拉力作用下,螺杆与锥头作为一个整体被往上拉,产生从套筒上侧拔出的趋势,使锥头与套筒间发生相对滑移。因此,自锁式单向螺栓的拉伸变形(柔度)可表示为
δsb=δlg+δtt+δslip
(1)
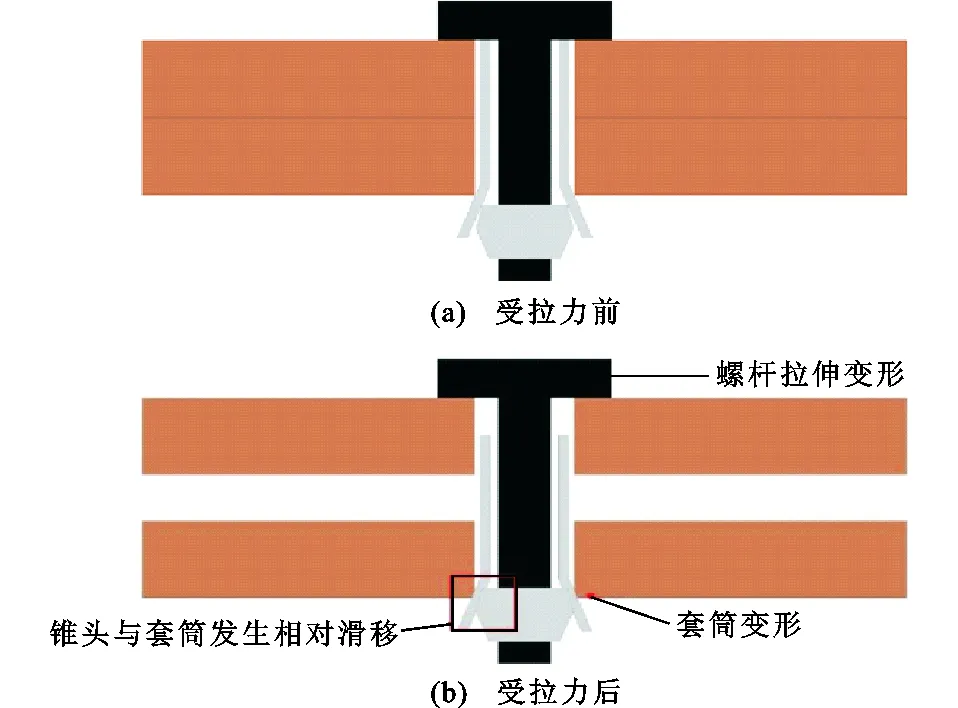
图5 自锁式单向螺栓受拉示意图Fig.5 Schematic Diagram of Self-lock One-side Bolt Under Tension
式中:δsb为单向螺栓的拉伸变形;δlg为螺杆的拉伸变形;δtt为套筒的变形;δslip为锥头与套筒间的相对滑移。
因此,自锁式单向螺栓的初始抗拉刚度可以通过这三部分的柔度系数来表达,即
(2)
式中:ksb为单向螺栓的初始抗拉刚度系数;klg为螺杆的抗拉刚度系数;ktt为套筒的径向变形刚度系数;kslip为锥头与套筒间相对滑移贡献的刚度系数。
4 自锁式单向螺栓初始抗拉刚度的理论计算模型
4.1 螺杆的抗拉刚度系数klg
标准螺杆的抗拉刚度系数klg可以参考欧洲规范[19]给出的计算公式,即
klg=1.6As/Lb
(3)
(4)
式中:As为螺杆的有效面积,对于SB16,As=157 mm2,对于SB20,As=245 mm2;Lb为螺杆长度;tT1,tT2为2块连接板厚度;tw1为钢垫圈厚度,对于SB16,tw1=8 mm,对于SB20,tw1=10 mm;tw2为橡胶垫圈厚度,对于SB16,tw2=5 mm,对于SB20,tw2=6 mm;th为螺栓头高度 ,对于SB16,th=5 mm,对于SB20,th=6 mm;tn为锥头高度 ,对于SB16,tn=18 mm,对于SB20,tn=22 mm。
因此,螺杆的抗拉刚度Klg为
Klg=klgE
(5)
式中:E为螺杆的弹性模量。
4.2 套筒的径向变形刚度系数ktt
文献[20]曾经计算了英国类似单向螺栓Hollo-Bolt的套筒变形,本文计算方法参考文献[20]的方法,并结合国产自锁式单向螺栓的实际情况改进而来。
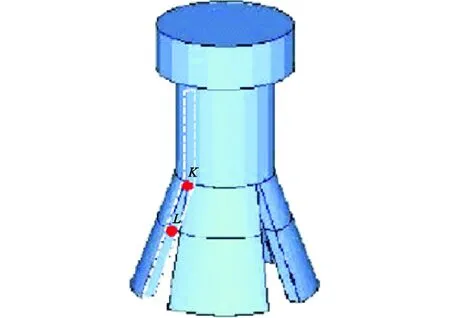
图6 套筒简图Fig.6 Schematic Diagram of Sleeve
由于套筒仅受到来自钢板与锥头的力,因此套筒的实际受力范围只有钢板与锥头之间的一小部分,如图6套筒中的K点和L点之间。将套筒沿径向剖开,取横截面进行受力分析,如图7所示,其中,s1为K点到套筒肢延长线与轴线交点的距离,s2为L点到套筒肢延长线与轴线交点的距离,dtcm为锥头最宽处直径,dtct为锥头顶部直径,α为套筒肢撑开的角度,qb为套筒与锥头的接触压应力,B为螺杆受到的力。
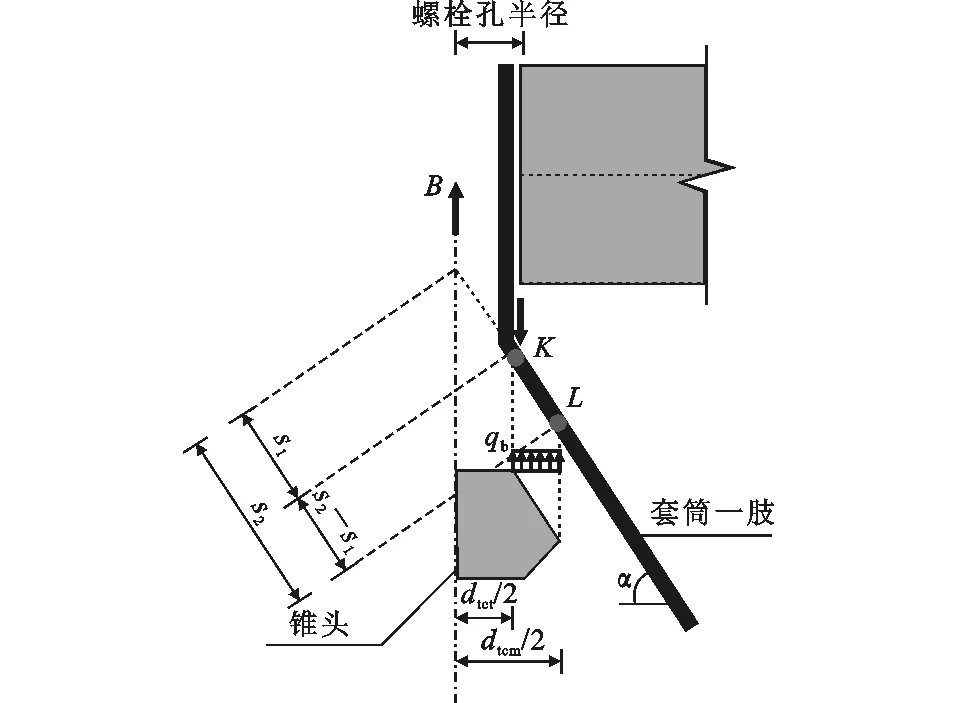
图7 套筒受力分析Fig.7 Stress Analysis of Sleeve
图7中,K点到L点间为套筒的受力段,钢板在K点把集中线荷载传递到套筒上,锥头在K点到L点间把分布面荷载传递到套筒上。从K点到L点间取出一段微元体进行分析,如图8所示,其中,s为套筒微元体到套筒肢延长线与轴线交点的距离,Ns为套筒微元体受到的径向合力,Nθ为套筒微元体受到的环向合力,ps为沿套筒径向的应力,pr为沿套筒法向的应力,r1,r2,R为尺寸参数。
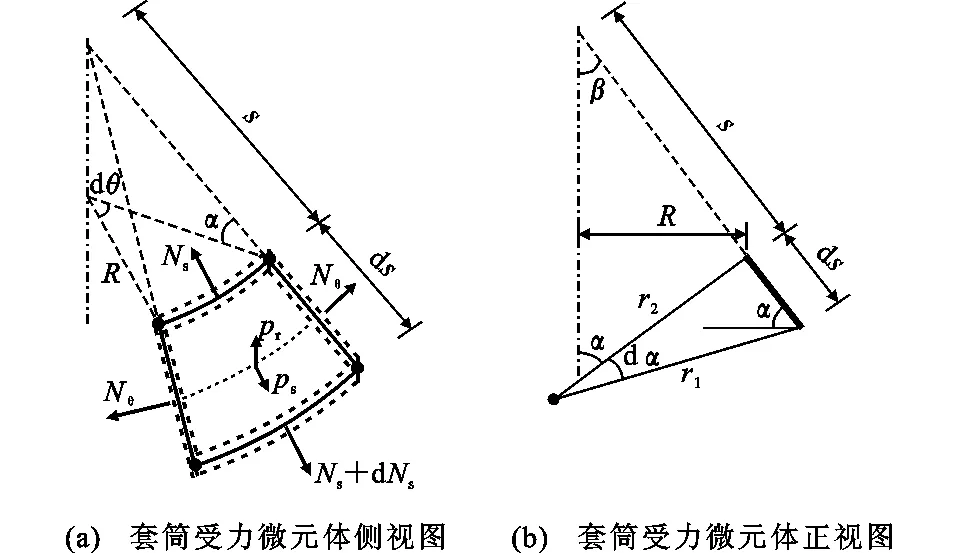
图8 套筒微元体分析Fig.8 Microelement Analysis of Sleeve
通过对力的分解,得
(6)
(7)
(8)
(9)
式中:Aslp为套筒与锥头在水平投影上的接触面积;γ为考虑套筒开缝的修正系数;对于SB16,dtcm=25 mm,对于SB20,dtcm=30 mm;对于SB16,dtct=19.2 mm,对于SB20,dtct=24.2 mm;bs为套筒开缝宽度,对于SB16,bs=1.3 mm,对于SB20,bs=1.6 mm。
对式(6),(7)进行积分,得
(10)
(11)
其中
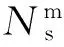
(12)
式中:对于SB16,ts=4.375 mm,对于SB20,ts=5.875 mm。
将式(10),(11)代入式(12),单元体在竖直方向的变形δy可以表示为
δy=-δxtan(α)=
(13)
单元体在竖直方向的最大位移可以认为发生在锥头与套筒接触区域的底部,因此,令s=s2,单元体在竖直方向的最大位移可以表示为
(14)
根据式(14),套筒的径向变形刚度系数ktt为
(15)
因此,套筒的径向变形刚度为
Klg=kttE
(16)
4.3 锥头与套筒间的相对滑移刚度系数kslip
首先把锥头与套筒的接触区域等效为一个圆形的接触区,如图9所示(其中,a为接触区域半径,c为黏着区半径),包含滑动区和黏着区,根据面积等效计算接触区域半径a,如式(17)所示。
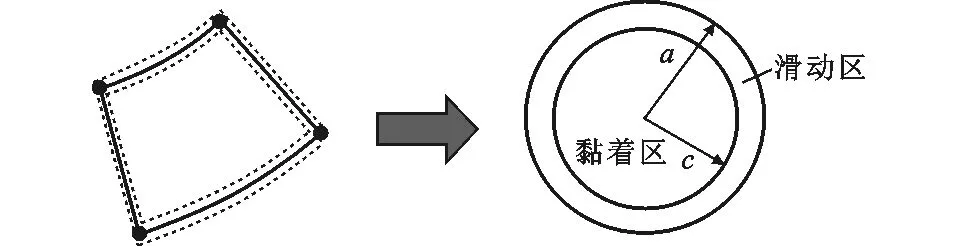
图9 等效接触区域Fig.9 Equivalent Contact Area
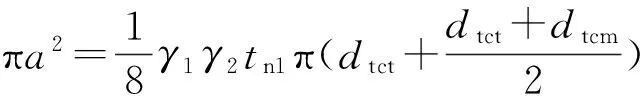
(17)
(18)
式中:γ1为考虑套筒开缝减少接触面积的修正系数;γ2为考虑锥头棱角减少接触面积的修正系数;tn1为锥头与套筒接触长度,tn1=3.7 mm;dnsl为套筒的内径,对于SB16,dnsl=17 mm,对于SB20,dnsl=21 mm。
接触面的法向应力和切向应力分布可表示为
pr=p0[1-(r/a)2]1/2
(19)
τr=τ(1)+τ(2)
(20)
(21)
τ(1)=τ1(1-r2/a2)1/2
(22)
τ(2)=-τ2(1-r2/c2)1/2
(23)
式中:τr为接触面上一点的切向应力;τ1,τ2为切向应力参量,可依据相应的边界条件确定;p0为接触面上的平均法向应力;FN为接触面上法向合力;τ(1),τ(2)为经典赫兹应力分布式。
根据赫兹应力理论,由应力pr,τr产生的表面微观位移ux为
(24)
式中:G为材料的剪切模量。
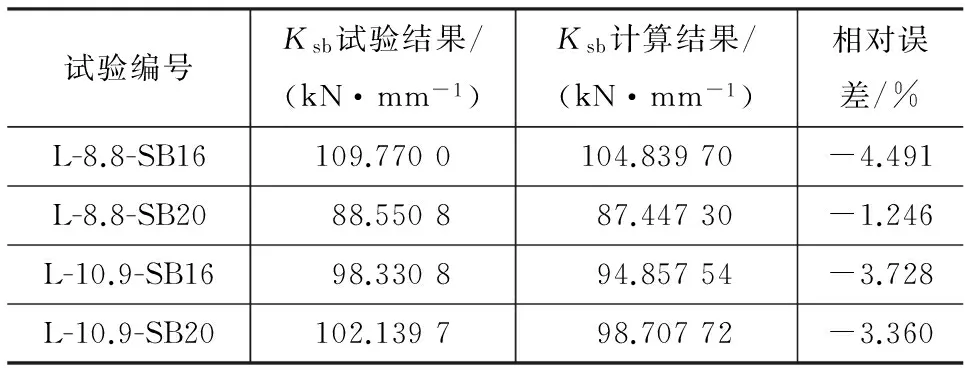
假定2个边界条件:①黏着区内位移恒定,ux(r)为常量,r 将边界条件代入式(19),(20),(24)可得 τ1=μp0 (25) τ2=μp0c/a (26) 切向应力τr在接触面内积分,切向力合力Fx为 (27) 式中:S为接触面积。 将式(21),(25),(26)代入(27),可得 (28) 将式(25),(26)代入式(24)中,可求得黏着区的位移为 (29) 因此,切向接触刚度Kslip为 (30) (31) 由于锥头与套筒间的摩擦因数μ与接触区域半径a较难确定,这里取不同的摩擦因数μ与接触区域半径a进行计算,观察μ,a对kslip的影响,结果如表4,5所示。 表4 摩擦因数μ对kslip的影响(a=1.4 mm)Tab.4 Impact of Friction Coefficient μ on kslip (a=1.4 mm) 表5 接触区域半径a对kslip的影响(μ=0.4)Tab.5 Impact of Contact Area Radius a on kslip (μ=0.4) 从表4,5可以看出:摩擦因数μ较小时(0.3~0.6)相比μ较大时(0.6~1.0)对kslip影响更大;接触区域半径a与kslip线性相关,相比摩擦因数μ对kslip影响更大。 至此,单向螺栓轴向抗拉刚度各部分刚度贡献已完成计算,可根据式(2)计算单向螺栓轴向抗拉刚度的理论值,并与试验值进行比较。 国产自锁式单向螺栓轴向抗拉刚度的理论计算结果与试验结果对比见表6。从表6可以看出,理论计算结果与试验结果吻合较好。 表6 抗拉刚度计算结果与试验结果对比Tab.6 Comparison of Calculation Results and Test Results of Tensile Stiffness (1)钢结构用国产自锁式单向螺栓的初始抗拉刚度由螺杆的拉伸变形、套筒的变形、锥头与套筒间的相对滑移三部分组成,其中最主要的影响因素为锥头与套筒间的相对滑移。 (2)锥头与套筒间接触区域的大小对自锁式单向螺栓初始抗拉刚度的影响较大。 (3)本文提出的自锁式单向螺栓抗拉刚度分析模型结果与试验结果吻合较好。 参考文献: [1]吴玉全,汪发.梁-钢管柱节点暗螺栓连接研究概述[J].低温建筑技术,2011(2):48-50. WU Yu-quan,WANG Fa.Overview of Research of Beam-hollow Column Joints with Blind Blots[J].Low Temperature Architecture Technology,2011(2):48-50. [2]TIZANI W,RIDLEY-ELLIS D J.The Performance of a New Blind-bolt for Moment-resisting Connections[C]// JAURIETTA M A,ALONSO A,CHICA J A.Tubular Structures X:Proceedings of the 10th International Symposium on Tubular Structures.Rotterdam:Balkema A A,2003:395-400. [3]TIZANI W,AL-MUGHAIRI A,OWEN J S,et al.Rotational Stiffness of a Blind-bolted Connection to Concrete-filled Tubes Using Modified Hollo-bolt[J].Journal of Constructional Steel Research,2013,80(1):317-331. [4]RAHMAN N A.Fatigue Behaviour and Reliability of Extended Hollobolt to Concrete Filled Hollow Section[D].Nottingham:University of Nottingham,2012. [5]TIZANI W,WANG Z Y,HAJIRASOULIHA I.Hysteretic Performance of a New Blind Bolted Connection to Concrete Filled Columns Under Cyclic Loading:An Experimental Investigation[J].Engineering Structures,2013,46:535-546. [6]MOURAD S.Behaviour of Blind Bolted Moment Connections for Square HSS Columns[D].Hamilton:McMaster University,1994. [7]HOOGENBOOM A J.Flow Drill for the Provision of Holes in Sheet Material:USA,US4454741[P].1984-06-19. [8]TABSH S W,MOURAD S,KOROL R M.Structural Safety of Ultra-twist Blind Fasteners in Tension[J].Canadian Journal of Civil Engineering,1997,24(2):211-217. [9]MIRZA O,UY B.Behaviour of Composite Beam-column Flush End-plate Connections Subjected to Low-probability,High-consequence Loading[J].Engineering Structures,2011,33:647-662. [10]LIU Y,MALAGA-CHUQUITAYPE C,ELGHAZO-ULI A Y.Behaviour of Beam-to-tubular Column Angle Connections Under Shear Loads[J].Engineering Structures,2012,42:434-456. [11]ELGHAZOULI A Y,MLAGA-CHUQUITAYPE C,CASTRO J M,et al.Experimental Monotonic and Cyclic Behaviour of Blind-bolted Angle Connections[J].Engineering Structures,2009,31:2540-2553. [12]王静峰,张琳,戴阳.半刚性钢管混凝土框架梁柱端板连接抗震性能试验研究[J].土木工程学报,2012,45(11):13-21. WANG Jing-feng,ZHANG Lin,DAI Yang.Seismic Experimental Study of End Plate Connections for Semi-rigid Concrete-filled Steel Tubular Frames[J].China Civil Engineering Journal,2012,45(11):13-21. [13]WANG J,SPENCER JR B F.Experimental and Analytical Behavior of Blind Bolted Moment Connections[J].Journal of Constructional Steel Research,2013,82:33-47. [14]李国强,段炼,陆烨,等.H 型钢梁与矩形钢管柱外伸式端板单向螺栓连接节点承载力试验与理论研究[J].建筑结构学报,2015,36(9):91-100. LI Guo-qiang,DUAN Lian,LU Ye,et al.Experimental and Theoretical Study of Bearing Capacity for Extended Endplate Connections Between Rectangular Tubular Columns and H-shaped Beams with Single Direction Bolts[J].Journal of Building Structures,2015,36(9):91-100. [15]BARNETT T C,TIZANI W,NETHERCOT D A.The Practice of Blind Bolting Connections to Structural Hollow Sections:A review[J].Steel and Composite Structures,2001,1(1):1-16. [16]LEE J,GOLDSWORTHY H M,GAD E F.Blind Bolted T-stub Connections to Unfilled Hollow Section Columns in Low Rise Structures[J].Journal of Constructional Steel Research,2010,66(8):981-992. [17]LEE J,GOLDSWORTHY H M,GAD E F.Blind Bolted Moment Connection to Sides of Hollow Section Columns[J].Journal of Constructional Steel Research,2011,67(12):1900-1911. [18]张杰华.钢结构用国产自锁式单向螺栓力学性能研究[D].上海:同济大学,2016. ZHANG Jie-hua.Research on Mechanical Properties of Domestic Self-lock One-side Bolt[D].Shanghai:Tongji University,2016. [19]EN 1993-1-8:2005,Eurocode 3:Design of Steel Structures.Part 1-8:Design of Joints[S]. [20]WANG Z Y,TIZANI W,WANG Q Y.Strength and Initial Stiffness of a Blind-bolt Connection Based on the T-stub Model[J].Engineering Structures,2010,32(9):2505-2517.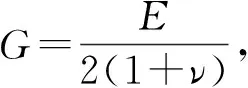


5 试验结果与理论计算结果对比
6 结语

