基于差分反演的综合孔径辐射计成像算法改进

张 颖 ，刘 浩 ，张 成 ，吴 季 ，何杰颖

（1.中国科学院国家空间科学中心微波遥感技术重点实验室，北京100190；2.中国科学院大学北京100049）

静止轨道干涉式毫米波大气探测仪主要面向静止轨道大气温度和湿度探测，预计工作于50～56 GHz。由于微波频段受云和降雨天气影响小，可以穿透大部分云层[1]，结合静止轨道上现有的红外和可见光探测仪，静止轨道干涉式毫米波大气探测仪能实现云内部温度和湿度垂直分布以及降水的探测[2]。另一方面，由于静止轨道卫星相对地球静止，能够对地球进行大面积的连续时间观测，因而能在地球大范围的的观测上获取极高的时间分辨率，在热带气旋和强降水等突发性强、持续时间较短的灾害性天气系统的实时监测、预报和预警上具有突出的能力。

由于静止轨道距离地球约为36 000公里，为实现与极轨卫星相当的空间分辨率，利用传统真实孔径辐射计的技术手段需要研制高精度大口径反射面天线，技术难度大。静止轨道干涉式毫米波大气探测仪采用干涉式综合孔径技术[3]，利用稀疏分布的小天线组成的圆环天线阵列代替传统辐射计的大口径真实孔径天线，克服了传统辐射计不适应静止轨道星载应用的缺陷，并且在空间分辨率上具有更好的拓展空间。近年来，干涉式综合孔径技术推动了静止轨道微波探测技术新一轮的发展，并逐渐成为国际上主流的发展方向。除中科院空间中心于2005年提出静止轨道干涉式毫米波大气探测仪的系统概念并开展样机研制外[4-5]，美国与欧洲也基于干涉式综合孔径技术分别提出了各自的星载系统概念（GeoSTAR及GAS），并研制了各自的地面缩比样机[6-9]。

静止轨道干涉式毫米波大气探测仪主要针对地球圆盘观测视场内的亮温分布进行成像，亮温成像的准确性将会影响到温度等大气参数的应用反演的准确性，是探测仪的一个主要性能指标。本文针对目前静止轨道干涉式毫米波大气探测仪的成像算法提出了基于差分反演的测量数据预处理方法，它能进一步降低现有成像算法的成像误差，有效改善亮温成像的质量。文中首先介绍静止轨道干涉式毫米波大气探测仪所采用的干涉式测量原理及目前使用的成像算法，然后论述基于差分反演的测量数据预处理方法，最后通过仿真结果论证该方法对于改善亮温成像质量的有效性并对全文进行总结。

1 干涉式测量原理

综合孔径干涉式测量的概念由射电天文领域引入，主要目的是用数量稀疏的小单元天线阵列获取高空间分辨率。与传统型辐射计直接对空间域进行亮温测量不同，干涉式测量从频域入手，首先获取空间频率域的采样信息，即对天线阵列中任意两个天线的接收信号进行复相关运算作为该天线对所对应的空间频率域采样点上的频域值。通过对天线阵列进行合理排布，使得阵列中所有天线对获取的采样信息能够覆满整个空间频率域空间，然后对采样信息进行傅里叶逆变换反演即可得到观测视场的亮温分布图像。干涉式测量中，空间频率域采样与空间域待观测的亮温分布通过公式（1）联系[10]。

其中V(ρ,φ)为空间频率域采样，它被称为可见度函数，空间频率域使用极坐标(ρ,φ)表示，它由该采样值对应的一对单元天线之间的间距决定，TB(ξ,η)为空间域待观测的亮温分布，(ξ,η)为空间域的方向余弦坐标，它由探测器与观测场景之间的空间几何关系决定，Trec为接收机的物理温度，D1和D2分别为两个天线的方向性系数，Fn1(ξ,η)和Fn2(ξ,η)分别为两个单元天线的归一化电压方向图，被称为空间去相关因子，表征接收机带宽很大而天线间距较远时，目标辐射信号传播到两个天线时的时间差所引起的相关运算中相关度的损失。

从公式（1）可以看出，可见度函数和待观测亮温之间有近似的傅里叶变换关系，理论上可以通过对可见度函数进行逆傅里叶变换反演得到重建亮温，然而由于静止轨道干涉式毫米波大气探测仪采用圆环阵列进行旋转分时采样，其空间频率域采样呈极坐标分布，针对极坐标形式的傅里叶公式，无法使用快速傅里叶变换进行快速计算。为了能快速而准确的计算二维极坐标下的傅里叶变换以便获取观测目标的反演亮温，静止轨道干涉式毫米波大气探测仪采用伪极逆傅里叶变换法（pseudo-polar IFFT）[11]进行亮温反演，具体步骤为首先将极坐标下的空间频率域采样插值到伪极网格上，然后利用伪极网格在角度方向按射线斜率均匀间隔分布，在轴线方向等距分布构成同心方形这一格点分布特性，通过两次一维傅里叶变换反演得到空间域图像，非常高效地实现亮温重建。

2 基于差分反演的测量数据预处理方法

为了进一步降低伪极逆傅里叶变换反演法得到的重建亮温的误差，可以采用基于差分反演的测量数据预处理方法，它包括平坦目标差分反演和重建亮温差分反演两种处理方案，其处理思想如图1所示。作为对比，图1（a）显示了不做测量数据预处理，仅使用伪极逆傅里叶变换法反演亮温的示意图，图中G表示探测仪观测目标即公式（1）的过程，G-1表示使用伪极逆傅里叶变换法从可见度函数测量值反演亮温的过程。图1（b）为平坦目标差分反演的示意图，与普通伪极逆傅里叶变换反演法的区别在于，首先针对平坦目标即亮温均匀分布的目标，进行与待观测目标相同的探测仪观测过程模拟，得到平坦目标对应的空间频率域采样后，将其与待观测目标对应的空间频率域可见度函数采样值相减，对此差分结果使用伪极逆傅里叶变换得到差分可见度函数对应的反演亮温，然后加上平坦目标的亮温以补偿空间频率域的差分过程。平坦目标差分反演方法中在可见度函数这一级进行差分的目的是为了使处理后的可见度函数的分布更为平缓，从而提高反演算法中极坐标向伪极坐标转换时可见度函数的插值的准确性，进而提高重建亮温的准确性。

图1（c）显示了重建亮温差分反演的过程，与图1（b）中平坦目标差分反演的区别在于将平坦目标替换为反演得到的重建亮温，即首先对可见度函数V进行一次亮温反演，得到后对其进行观测过程模拟，将这一步得到的可见度函数将反馈回待观测目标对应的可见度函数V，并与之相减，然后执行与平坦目标差分反演相同的处理步骤，得到重建亮温后再将其作为新的差分对象，继续下一轮的重建亮温差分反演，以此循环。通过上述描述可知，首次得到的反演亮温，这里将其称为0阶反演亮温，即为图1（a）中未做任何处理、仅通过伪极逆傅里叶变换法得到的重建亮温，而随着图1（c）所示循环迭代的次数增加，即反演亮温的阶数增加，反演亮温将逐渐接近真实待观测亮温的分布，二者之间的误差也将不断降低。

图1 基于差分反演的测量数据预处理方法示意图

3 仿真结果及分析

使用由MATLAB搭建的静止轨道干涉式毫米波大气探测仪的仿真系统[12]，并利用美国国家环境预报中心的全球最终分析资料[13]、数值天气预报模式WRF[14]和快速辐射传输模型RTTOV[15]实现地球圆盘观测视场的目标建模仿真[16]，模拟贴近真实大气情况的观测目标亮温，作为探测仪仿真系统的输入观测目标亮温，则可以通过仿真的手段评估基于差分反演的测量数据预处理方法的有效性。为了使平坦目标的亮温值尽量接近待观测场景的亮温，一般利用目标建模仿真手段获取的亮温分布先验信息计算出地球圆盘亮温分布的均值，将之作为平坦目标的亮温值。

图2 50.3 GHz和54.4 GHz时，待观测亮温及3种方法重建亮温

图2以50.3 GHz和54.4 GHz为例，分4列分别显示了待观测亮温、未使用差分反演方法的重建亮温、使用平坦目标差分反演处理后的重建亮温和使用重建亮温差分反演得到的重建亮温，其中后者只执行了一次差分反演迭代，即得到的是一阶重建亮温。对比图2的4列图像可以看出，使用基于差分反演的测量数据预处理方法后，得到的重建亮温与待观测亮温非常接近，并且54.4 GHz结果可以非常明显的看出，相比未使用该处理方法得到的反演亮温，该处理方法能够明显降低地球圆盘边缘区域的亮温反演误差，改善亮温反演的效果。

图3通过柱状图对比显示了未使用差分反演方法的重建亮温误差，使用平坦目标差分反演处理后的重建亮温误差和使用重建亮温差分反演得到的重建亮温误差，其中针对后者展示了3次迭代处理对应的一阶/二阶/三阶重建亮温误差，此处均以待观测亮温作为基准，通过图像间的均方根差异来衡量重建亮温误差。

图3 3种方法的重建亮温误差随探测频率的分布柱状图

图3中可以看到平坦目标差分反演相比未做差分处理的反演亮温误差有所降低，总体而言，重建亮温差分反演的亮温误差比平坦目标差分反演误差又进一步有所降低，由此可见，通过空间频率域测量数据的差分处理，使进入反演算法环节的可见度函数更加平缓，能够显著降低反演亮温误差，改善重建亮温图像质量。而对比不同阶数的重建亮温差分反演的误差可知，随着该方法中循环迭代次数的增加，反演亮温的误差能逐渐降低。从图中重建亮温差分反演结果的三阶重建亮温误差与二阶重建亮温误差之间的关系可以反映出，当循环迭代达到一定次数时，继续进行迭代误差将不再有明显改善。具体在实际过程中迭代次数的选择需要对计算资源、反演亮温的准确性需求、以及获取反演亮温的时效性等因素综合考虑来设定。从以上结果来看，重建亮温差分反演时进行两次迭代是一个合理的选择。为了量化显示以上结果，表1列出了图3中显示的3种处理方法共5组处理方案在50～56 GHz 7个探测频率的均方根误差值。

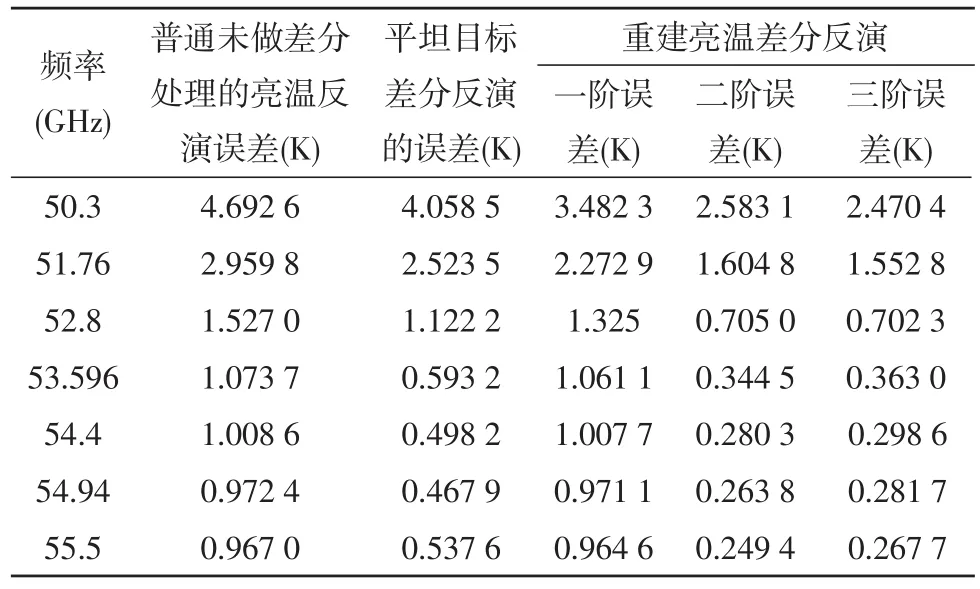
表1 普通未做差分处理和3种方法的反演亮温误差对比

4 结论

文中针对静止轨道干涉式毫米波大气探测仪，提出了基于差分反演的测量数据预处理方法以降低亮温成像误差。首先对静止轨道干涉式毫米波大气探测仪的测量原理和成像算法进行说明，然后论述了基于差分反演的测量数据预处理方法的思想和处理流程，并结合探测仪仿真系统和目标建模，通过仿真手段对该数据预处理方法进行了验证，仿真结果表明，使用平坦目标和重建亮温对应的可见度函数对测量数据进行差分处理，能够显著降低反演亮温误差，尤其在地球圆盘观测视场的边缘能使重建亮温更贴近待观测目标的亮温分布，有效改善重建亮温的图像质量。

参考文献：

[1]何杰颖，张升伟.地基和星载微波辐射计数据反演大气湿度[J].电波科学学报，2011，26（2）：362-369.

[2]谷松岩，郭杨，游然.FY-3A/MWHS辐射传递及冷空偏差修正[J].遥感技术与应用，2015，30（2）：251-257.

[3]Martin-Neira M，LeVine D M，Kerr Y，et al.Microwave interferometric radiometry in remote sensing：An invited historicalreview[J].Radio Science，2014，49（6）：415-449.

[4]LIU H，WU J，ZHANG S W，et al.The Geostationary Interferometric Microwave Sounder（GIMS）：Instrument overview and recent progress[C]//Proc.IGARSS，2011：3629-3632.

[5]ZHANG C，LIU H，WU J，et al.Imaging analysis and first results of the geostationary interferometric microwave sounder demonstrator[J].IEEE Trans.Geosci.Remote Sens.，2015，53（1）：207-218.

[6]A Colliander，T Narhi，P de Maagt.Modeling and analysis of polarimetric synthetic aperture interferometric radiometers using noise waves[J].IEEE Trans.Geosci.Remote Sens.，2010，48（9）：3560-3570.

[7]郭玲华，邓峥，陶家生，等.国外地球同步轨道遥感卫星发展初步研究[J].航天返回与遥感，2010，31（6）：23-30.

[8]TANNER A，Gaier T，Imbriale W，et al.A dualgain design for the geostationary synthetic thinned array radiometer[J].IEEE Geoscience and Remote Sensing Letters，2014，11（8）：1340-1344.

[9]Todd G，Pekka K，Bjorn L，et al.A 180 GHz pro⁃totype for a geostationary microwave imager/sound⁃er-GeoSTAR-III[C].2016 IEEE International Geoscience and Remote Sensing Symposium（IGARSS），2016：2021-2023.

[10]Corbella I，Martin-Neira M，Oliva R，et al.Re⁃duction of secondary lobes in aperture synthesis ra⁃diometry[J].IEEE Geoscience and Remote Sensing Letters，2012，9（5）：977-979.

[11]ZHANG C，LIU H，Yan J Y，et al.Imaging algorithm and experimentaldemonstration of rotating scanning interferometric radiometer[C]//Proc.IGARSS，2010：534-537.

[12]ZHANG Y，LIU H，WU J，et al.Method to reduce imaging errors in dynamic target observation of the geostationary interferometric microwave sounder[J].IEEE Geoscience and Remote Sensing Letters，2017，14（2）：267-271.

[13]柏枫，谌孙荣，陈邦怀，等.NCEP FNL分析资料本地化应用系统设计与实现[J].计算技术与自动化，2013，32（3）：141-144.

[14]Jarno M，Bormin H，Hung-lung A H，et al.GPU acceleration of the updated goddard shortwave radi⁃ation scheme in the Weather Research and Fore⁃casting（WRF）model[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2012，5（2）：555-562.

[15]Tanvir I，Prashant K，George P P.Uncertainty quantification in the Infrared Surface Emissivity Model（ISEM）[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2016，9（12）：5888-5892.

[16]Zhang Y，LIU H，WU J，HE J Y，et al.Target brightness temperature simulation and analysis for the geostationary interferometric microwave sound⁃er（GIMS）[C]//Proc.IGARSS，2015：3477-3480.