双轮差速移动机器人轨迹跟踪混合控制算法研究*
许 万,曹 松,罗 西,王 琪,杨 维
(湖北工业大学 机械工程学院,武汉 430068)
0 引言
随着国家对工业智能化的重视,轮式移动机器人在服务、物流、探测等领域具有极广的应用前景,而对具有非完整系统的移动机器人的运动控制是关注的热点。轨迹跟踪问题作为其控制的重要研究问题,受到研究者的广泛关注。轨迹跟踪是使移动机器人的实际轨迹快速且稳定地跟踪上期望轨迹,问题的解决即是要设计出合理的控制器,以满足移动机器人的性能要求。而在实际应用中,由于移动机器人自身的结构和系统以及外部的不确定因素,要达到理想的跟踪效果,就显得困难重重。
文献[1-2]提出了一种基于Backstepping的控制方法,计算出合适的目标速度,并在此基础上加上最小均方算法作为观测器,实现了最小化轨迹跟踪误差。文献[3-4]运用终端滑动模态技术,提出基于滑模控制的轨迹跟踪控制策略,采用基于反算法的有限时间控制方法,提高了轨迹跟踪的收敛性能。由于滑模变结构具有不连续性的本质,引起控制系统的抖振将是不可避免的。文献[5-7]则针对抖振和收敛速度,提出了新型滑模变控制策略,在解决了系统中未知参数带来的影响基础上,抖振现象也被有效地抑制了,且较好地消除了跟踪误差。文献[8]提出了基于优化方法的模糊反演控制器在轨迹跟踪问题中的应用,利用动力学模型设计出力矩的控制律,达到了良好的跟踪效果。
以上所述的控制算法,部分只运用了移动机器人的运动学模型,若应用于重载移动机器人则存在明显不足;部分算法结合了动力学模型,但是均涉及到力矩法,需要精确的力矩模型。本文在上述的研究基础上,针对双轮差速移动机器人,提出了基于前馈运动学和基于干扰观测器的解耦动力学的轨迹跟踪混合控制算法,该算法无需精确模型,即可取得良好的轨迹跟踪性能。在运动学控制器中,采用位姿输入的前馈控制,保证轨迹跟踪的快速收敛;在动力学控制器中,采用前馈解耦补偿器,将力矩控制律的设计转变为新的辅助量控制律的设计,加入干扰观测器,增强控制器的鲁棒性,运用具有积分链式结构微分器,抑制求导带来的噪声影响,在速度上保证移动机器人的跟踪性能。最后将该算法运用到工程应用中,验证其可行性。
1 移动机器人系统建模
1.1 移动机器人运动学建模

图1 双轮差速移动机器人运动学模型
在理想情况下,具有非完整约束的移动机器人相对于局部坐标系中YR轴的速度分量为0,即移动机器人的一个运动约束方程为:

(1)
则移动机器人的运动学模型满足等式:

(2)
1.2 移动机器人动力学建模
考虑一个具有n个自由度并且受到m(1≤m (3) 结合第1.1节可推算出: (4) (5) 从式(5)可以看出,在动力学模型中,控制输入量是力矩τ。 (6) 通过坐标转换,可得到在局部坐标系中双轮差速移动机器人的位姿误差e为: (7) 图2 移动机器人在局部坐标系中的位姿误差示意图 结合式(2),对局部位姿误差,即式(7)进行求导可得: (8) 移动机器人运动学模型的输入可设计为: (9) 等式右边的前半部分作为前馈输入,后半部分v1和v2则作为新的反馈闭环控制系统的输入。 把式(9)代入式(8),并在平衡点(e1=e2=e3=0,v1=v2=0)处进行线性化,可以得到以局部位姿误差为状态变量的状态方程: (10) 对式(10)所描述的输入V设计新的闭环系统控制律: V=Ke (11) 因该状态方程有三个状态变量和两个输入,则增益矩阵K的维度为2×3。 对式(11)定义的控制律可设计为: (12) 若只考虑运动学模型,则该控制器的结构框图设计如图3所示: 图3 基于前馈运动学控制器的结构框图 本文在动力学控制器中串联了一个前馈解耦补偿器;同时,引入带有扰动观测器[10]的二自由度控制系统[11]。 (13) 基于前馈补偿器解耦的转换控制框图如图4所示: 图4 基于前馈补偿器解耦的转换控制框图 由图4可以看出,将对力矩τ控制律的设计转换成为对辅助控制矢量z控制律的设计,本文所设计的辅助控制矢量z的控制律为: (14) 式中,Kp=diag(kpv,kpω),Kd=diag(kdv,kdω) 其动力学控制器的结构框图,如图5所示。 图5 带有观测器的解耦动力学控制器的结构框图 从图5可以看出,经过前馈解耦的动力学控制器组成还包括前馈控制器与PD反馈控制器组成的二自由度控制系统和扰动观测器。其中,前馈控制对运动学控制器的速度输出做了系统逆运算,计算得到的系统输入能够使动力学控制器的速度输出精确跟踪运动学控制器的速度输出并且能够保证系统内部稳定,从而提高了系统的跟踪性能。同理,扰动观测器动力学控制器的速度输出做了系统逆运算,再与辅助控制输入作比较,观测出等效扰动,再反馈到辅助控制的输入端,从而抵消外部扰动,进一步保证了系统的鲁棒性。另外,在控制律式(14)中需要对输入信号求导,本文采用二阶线性积分链式微分器[12]来实现,其定义如下: (15) 式中,N(t)为待微分的输入信号;x1为对信号进行跟踪;x2为信号一阶导数的估计;微分器的初始值为x1(0)=0,x2(0)=0。 噪声一般存在于信号中进入微分器,由式(15)可以看出,只有微分器底层的微分方程中存在噪声。在工程应用中,具有积分链式结构的微分器,对含有噪声的信号求导时,噪声只含在微分器的最后一层,通过积分作用,信号一阶导数中的噪声能够被更充分地抑制。 2.3.1混合控制器设计 针对双轮差速移动机器人轨迹跟踪问题,本文提出了一种基于前馈运动学和带有干扰观测器的解耦动力学的混合控制算法,把动力学控制器作为内环加入到运动学控制器中,并给出混合控制器系统框图,如图6所示。 图6 非完整移动机器人轨迹跟踪控制器系统框图 2.3.2稳定性分析 本文对2.3.1节提出的混合控制器,用Lyapunov(李雅普诺夫)函数直接法来分析其稳定性。 首先,取k2>0,式(12)可写为: v1=-k1e1 v2=-k2vde2-k3e3 (16) 移动机器人的实际速度与运动学控制器的输出期望速度的误差为速度跟踪误差,定义为: (17) 式(14)可化简为: (18) 最后选取局部位姿误差e1、e2、e3和速度跟踪误差ev、ew作为混合系统的状态变量,则混合系统的状态方程可写为: (19) 由式(19)可得,混合系统在e1=e2=e3=ev=ew=0处具有唯一的平衡状态。选取总的Lyapunov函数为: (20) 假设该函数对所有局部位姿误差e1、e2、e3和速度跟踪误差ev、eω都具有一阶偏导数。当且仅当e1=e2=e3=ev=eω=0时,恒有V(e′)=0;当e1、e2、e3、ev、ew不全为零时,V(e′)>0,则V(e′)为正定的。 对式(20)求导并结合式(19)得: (21) 表1 轨迹跟踪控制器参数选取 图7所示为仿真的效果图: (a) 轨迹跟踪示意图 (b) 通过混合控制算法得出的速度 (c) 轨迹跟踪位姿误差图7 移动机器人轨迹跟踪控制器仿真图 图7b所示为通过轨迹跟踪混合控制算法计算得出的移动机器人右轮速度vR、左轮速度vL、线速度v和角速度ω,可看出,均能够快速稳定跟踪上给定的速度值。图7c所示为位姿误差,可得,存在初始误差的情况下,移动机器人通过控制器能够快速使位姿误差收敛,且趋于0;在持续1.5s的外部干扰下,结合图7a,机器人保持较好的稳定性,在干扰过后位姿误差能够快速收敛。 对于3.1节的仿真结果,是将双轮差速移动机器人处于理想环境下得到的,而在实际应用中,系统自身和外界因素的影响是不可忽视的。 图10 移动机器人轨迹跟踪控制器验证图 为了验证本文所提出的轨迹跟踪控制算法的可行性,结合仿真的设计,将算法移植到实际的移动机器人控制中。 3.2.1样机构成 图8所示为本文研究对象的整体控制系统示意图。该系统为自动导航系统,其中,负责路径规划的上位机通过WLAN(Wireless Local Area Networks)与地面控制系统进行交互;移动机器人的实际位姿由激光扫描仪NAV350获取并通过RJ45与主控制器通讯;主控制器为基于Windows XPe的嵌入式控制器,主控制器与驱动器、驱动器与驱动电机之间通过CAN (Controller Area Network)总线进行通讯。图9所示为本文所研发的双轮差速移动机器人车体,车体有四个车轮,前两轮为驱动轮,后两轮为万向轮,激光扫描仪安装在两驱动轮中轴线的正上方。移动机器人车体参数见表2。 图8 控制系统示意图 图9 双轮差速移动机器人 表2 移动机器人车体参数 3.2.2验证结果 图10b所示为移动机器人的位姿跟踪误差,图中可以明确看出局部坐标XR轴方向上的误差e1在除去起点位置之外有3个跳变的点,这是由于在程序设计时认为当移动机器人到达某个范围之内即表示到达了该点,而实际并没有完全到达点的坐标位置,所以会有一个跳变误差,即使这样,机器人的位姿误差仍可以快速收敛于0,跟踪上期望轨迹。从图10b可以看出,移动机器人稳定运行时的左右摆差为±9mm,停车误差可控制在以终点为圆心,9mm为半径的范围内。图10c、图10d所示为移动机器人实际的左右轮速度、线速度和角速度与理论的左右轮速度、线速度和角速度,由于初始位姿和初始速度值的不同,导致在运行起始阶段实际速度有一定的波动,但机器人的实际速度在6s左右可跟踪上理论速度,体现了快速收敛的性质,同时通过实际速度与理论速度曲线的拟合程度可看出,移动机器人在速度的跟踪上具有良好的实时性和跟踪效果。图10e所示为移动机器人的速度跟踪误差,可看出,从起始位置开始通过快速的动态调整过程后,速度跟踪误差稳定在0附近。综上所述,结合图10a的实际轨迹跟踪图,说明本文提出的基于前馈运动学和带有干扰观测器的解耦动力学的混合轨迹跟踪控制算法具有良好的跟踪效果和抗干扰能力,可行性也得到了验证。 本文将双轮差速移动机器人作为研究对象,在充分考虑系统自身和外部干扰因素的影响下,系统地介绍了基于前馈运动学和带有干扰观测器的解耦动力学的混合控制算法,在无需得到精确力矩模型的情况下,解决了移动机器人的轨迹跟踪问题。仿真结果表明,基于该算法所设计的轨迹跟踪控制器可实现良好的跟踪性能和鲁棒性,验证了其有效性。验证结果表明,存在初始误差时,移动机器人可快速调整到稳定状态,达到了良好的跟踪性能;存在外部干扰时,也可以平稳运行,具备了较好的抗干扰能力,实现了较好的控制效果,验证了该控制器的可行性。对于同样具有非完整系统的研究,本文提出的算法具有一定的借鉴价值。 [参考文献] [1] Kanayama Y, Kimura Y, Miyazaki F, et al. A stable tracking control method for an autonomous mobile robot[C]// IEEE International Conference on Robotics and Automation, 1990. Proceedings. IEEE Xplore, 1991:384-389. [2] Anushree R, Prasad B K S. Design and development of novel control strategy for trajectory tracking of mobile robot: Featured with tracking error minimization[C]// IEEE India Conference. IEEE, 2016:1-6. [3] 李世华,田玉平.移动小车的轨迹跟踪控制[J].控制与决策,2000,15(5):626-628. [4] 张扬名,刘国荣,杨小亮.基于滑模变结构的移动机器人轨迹跟踪控制[J].计算机工程,2013,39(5):160-164. [5] 席雷平,陈自力,齐晓慧.具有抖振抑制特性的机械臂快速滑模变结构控制[J].电机与控制学报, 2012, 16(7):97-102. [6] Jia P, Song C, Zhang X. Control and simulation of adaptive global trajectory tracking for nonholonomic mobile robots with parameter uncertainties[C]// International Symposium on Instrumentation & Measurement, Sensor Network and Automation. IEEE, 2012:314-317. [7] 王宗义,李艳东,朱玲.非完整移动机器人的双自适应神经滑模控制[J].机械工程学报,2010,46(23):16-22. [8] Swadi S M, Tawfik M A, Abdulwahab E N, et al. Fuzzy-Backstepping Controller Based on Optimization Method for Trajectory Tracking of Wheeled Mobile Robot[C]// Uksim-Amss, International Conference on Computer Modelling and Simulation,2016:147-152. [9] 唐述博. 非完整移动机器人点镇定和轨迹跟踪控制研究[D]. 大连:大连理工大学,2005. [10] Kempf C J, Kobayashi S. Disturbance observer and feedforward design for a high-speed direct-drive positioning table[J]. IEEE Transactions on Control Systems Technology, 2002, 7(5):513-526. [11] 彭超.基于系统逆的鲁棒二自由度控制方法研究[D].成都:电子科技大学,2012. [12] 王新华,刘金琨.微分器设计与应用[M].北京:电子工业出版社,2010. (编辑李秀敏)

1.3 移动机器人位姿误差建模
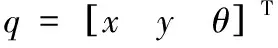

2 移动机器人轨迹跟踪控制器设计
2.1 运动学控制器设计

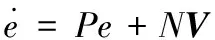

2.2 动力学控制器设计




2.3 混合控制器设计及稳定性分析



3 仿真和样机验证
3.1 仿真





3.2 样机验证





4 总结

