钢管混凝土拱桥稳定极限承载力的线弹性迭代方法
解威威,叶志权,杨绿峰
(1.广西大学 土木建筑工程学院,广西 南宁 530004;2.广西大学 教育部工程防灾与结构安全重点实验室,广西 南宁 530004)
钢管混凝土拱桥具有造型美观、承载力高、跨越能力强等优点。2001年我国建成首座铁路钢管混凝土拱桥——水柏铁路北盘江大桥[1],此后钢管混凝土拱桥在铁路桥的建设中得到了越来越广泛的应用。钢管混凝土拱桥的稳定承载力是桥梁设计中重点关注的问题。
拱桥稳定承载力的研究方法主要分为三类:试验法、解析法和数值法。
试验法能够真实地模拟拱桥的受力状态,从而获取拱桥的荷载位移曲线与失稳模态,其结果常作为检验其余方法准确性的基准。陈宝春[2]以实桥为原型,探讨了钢管混凝土拱肋分别在单点加载和两点非对称加载情况下的稳定极限承载力,并分析了拱肋在不同荷载条件下的失稳模态。Liu等[3]研究了矢跨比对抛物线钢管混凝土拱肋极限承载力的影响规律,且分析了不同矢跨比下拱肋的破坏模式。但试验法模拟的工况有限,且需要消耗大量的人力和物力。
解析法旨在建立拱桥稳定承载力的设计公式,常将拱肋等效为纯压柱或是压弯柱,进而结合钢管混凝土柱的承载力相关方程验算拱肋的稳定性是否满足要求。由于钢管混凝土拱轴线常为圆弧、抛物线或悬链线,与直柱的几何形状和受力状态有较大差异[3],因此拱肋稳定系数显著区别于柱的稳定系数。为此,韦建刚等[4]根据初始几何缺陷和矢跨比的影响建立了拱肋稳定系数的计算公式,并结合钢管混凝土稳定承载力相关方程建立了钢管混凝土压弯拱非线性临界荷载的等效梁柱法。同时,GB 50923—2013《钢管混凝土拱桥技术规范》(简称钢管混凝土拱桥规范)针对钢管混凝土拱肋给出了稳定系数的计算公式,Wu等[5]通过引入矢跨比的影响对拱桥规范稳定系数公式进行了修正。总体来说,解析法原理清晰,使用方便,但难以应用于复杂工程结构。
数值分析方法能够有效克服模型试验和解析法在适用性方面的缺陷。目前,钢管混凝土拱桥稳定极限承载力分析的常用数值分析模型包括双材料模型[2-3,5-7]和单一组合材料模型[2]两类,其中双材料模型利用钢管单元和混凝土单元能够准确分析2种材料不同的本构关系及非线性力学性能,物理意义明确,但需要引入2种材料之间的协调变形条件,理论复杂,且离散自由度较高,计算效率低。而单一组合材料模型基于钢管混凝土统一理论[8]和钢管混凝土组合材料本构关系,采用单一组合材料梁单元分析钢管混凝土结构的极限承载力,能够一定程度上提高计算效率。然而,无论单一组合材料模型还是双材料模型都需要依托增量非线性有限元法分析钢管混凝土结构极限承载力。由于增量非线性有限元法属于非线性迭代分析方法,对离散网格、单元类型、收敛容差和迭代算法的选择较为敏感,导致迭代收敛速度慢、计算结果有时不稳定,计算效率和精度较低,难以应用于工程实践。
为了克服增量非线性有限元法的缺陷,国内外发展了多种基于塑性极限理论的弹性模量调整法,包括mα-Tangent[9]、弹性补偿法[10]和弹性模量缩减法[11-12]等。该类方法通过调整弹性模量实现结构内力重分布,并利用线弹性迭代分析获得结构的极限承载力,从而避免了增量非线性有限元法依赖于非线性分析导致的缺陷,能够取得较高的计算效率和精度。为使用大尺寸单元模型,Hamilton和Boyle[13],Yang等[11-12]先后将广义屈服函数引入弹性模量调整法中,降低了离散未知量。但是,现行广义屈服函数大多为非齐次函数,不满足弹性模量调整法分析要求的比例条件,导致弹性模量调整法计算结果不稳定,精度受损。为此,Yang等[12]针对广义屈服函数进行齐次化处理,建立齐次广义屈服函数,克服了广义屈服函数的缺陷。然而,现行的齐次化策略[12]只针对含无量纲内力项的广义屈服函数,当考虑钢管混凝土拱桥稳定因素影响时,由于广义屈服函数与拱肋几何参数和材料参数相关,从而给齐次化处理带来困难。
为此,本文研究建立新的广义屈服函数齐次化策略,用于具有不同几何和材料特性的钢管混凝土拱桥稳定性分析,并结合弹性模量缩减法研究建立钢管混凝土拱桥稳定极限承载力分析的线弹性迭代方法。
1 钢管混凝土构件齐次广义屈服函数
1.1 压弯稳定承载力相关方程
对于图1所示的圆形钢管混凝土构件,文献[8]基于统一理论建立了构件截面的压弯稳定承载力相关方程。
(1)
其中,
Npx=AscfscyMpy=γmWscfscy

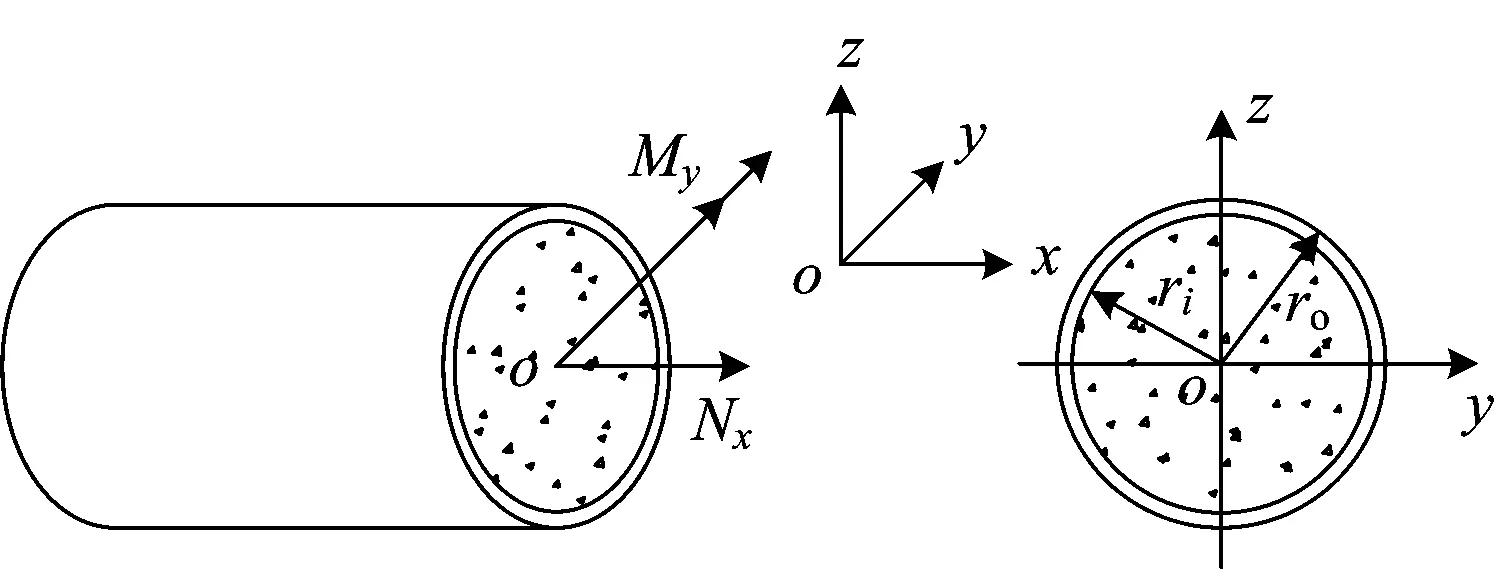
图1 截面内力示意图
度;Es为钢材弹性模量;ri为钢管内半径。
需要特别注意长细比λ表达式中的l0,对于受压杆件l0取其有效长度,对于钢管混凝土拱桥取l0=μslg,其中μs为等效计算长度系数,按钢管混凝土拱桥规范取为0.36,lg为钢管混凝土拱轴线长度。
1.2 拱桥稳定系数φ
文献[8]给出了式(1)用于钢管混凝土柱稳定承载力分析时稳定系数φ的取值,但是当式(1)用于钢管混凝土拱肋稳定承载力分析时,参数φ应按照钢管混凝土拱稳定系数取值。韦建刚等[4]根据矢跨比和初始缺陷影响定义钢管混凝土拱的稳定系数为
φ=K1K2
(2)
式中:K1和K2分别为钢管混凝土拱桥的矢跨比影响系数和初始几何缺陷影响系数。
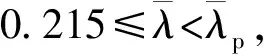
(3)
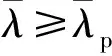
(4)
其中,
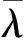
钢管混凝土拱桥规范另外给出的稳定系数φ的计算公式为
(5)
其中,
式中:λn为相对长细比。
Wu等[5]引入矢跨比的影响,对式(5)进行了修正,为
(6)
1.3 广义屈服函数
广义屈服准则是判断钢管混凝土构件进入全截面塑性屈服的重要依据,也是开展钢管混凝土拱桥极限承载力分析的基础,结合式(1)可建立钢管混凝土构件的广义屈服准则
f(nx,my)=1
(7)
其中,
式中:nx和my分别为轴力和弯矩的无量纲内力。
结合式(1)、式(7)可得钢管混凝土压弯构件稳定广义屈服函数为
f(nx,my)=
(8)
其中,
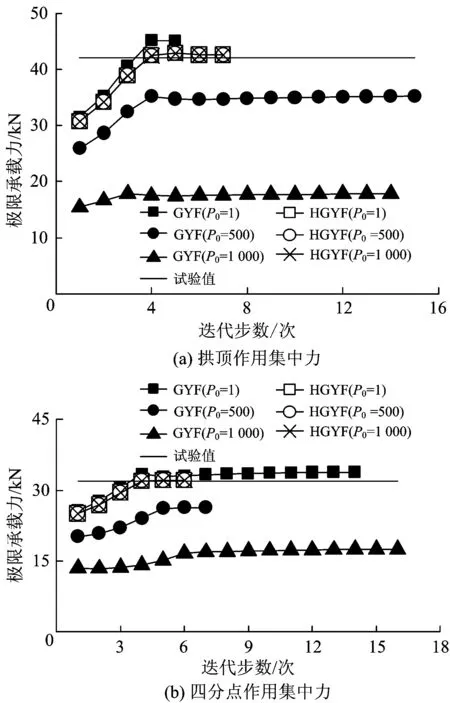
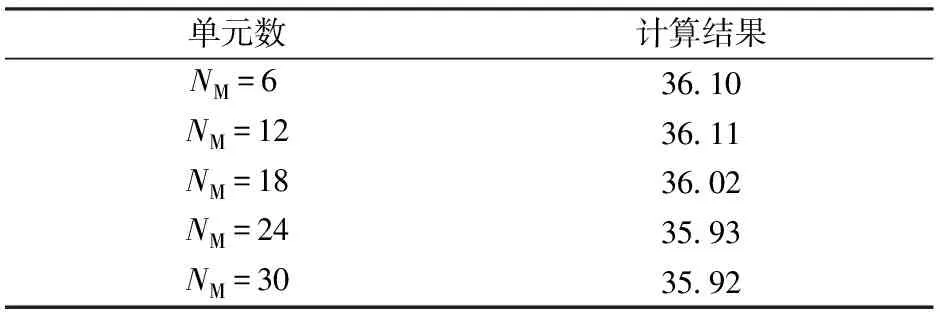
由于稳定系数φ的取值范围为(0,1)且有φNpx 由式(8)可以看出,压弯内力组合作用下的广义屈服函数是分段非齐次的,不满足结构极限分析的比例条件[12],将导致弹性模量调整法计算结果受荷载初值影响,出现计算精度受损等问题,因此有必要对广义屈服函数进行齐次化处理。然而,式(8)定义的钢管混凝土压弯构件的广义屈服函数中不仅含有无量纲内力,而且含有物理量aE,与稳定系数、长细比和材料强度等有关,因而广义屈服函数将随着钢管混凝土构件几何参数和材料参数的变化而发生改变。如果采用传统的齐次化方法,需要对具有不同几何参数和材料参数的圆形钢管混凝土构件的广义屈服函数重复进行齐次化处理,无法得到具有广泛适用性的齐次广义屈服函数。 为此,这里将aE作为参变量,将原有二维齐次化拟合扩展至三维。由此建立齐次广义屈服函数为 (9) 其中, (10) 取极小值,即可分析确定齐次广义屈服函数的待定系数。据此可定义残差均方差δ为 (11) 表1 均方差 (12) 其中, 式中:c1—c5为系数。 图2 aE=0.5时压弯广义屈服函数及其齐次化 图3 计算值Nuc和试验值Nut的比较 利用单一组合材料线弹性梁单元(ANSYS单元库中的BEAM189单元)建立钢管混凝土拱桥稳定极限承载力分析的数值模型,进而利用弹性模量缩减法计算钢管混凝土拱桥结构极限承载力。 弹性模量缩减法能够通过有策略地缩减钢管混凝土拱桥中高承载单元的弹性模量,模拟钢管混凝土拱桥在加载过程中的刚度损伤,并利用线弹性迭代分析计算钢管混凝土拱桥的稳定承载力。对于承受n个荷载P1,P2, …,Pn作用的钢管混凝土拱桥结构,可用向量P表示荷载为 P=P0αi=P0[α1,α2,…,αn]T (13) 式中:P0和αi分别为荷载基准值和荷载乘子。 (14) 式中:k为迭代步;e为单元编号。 (15) 其中, 式中:rkmax为结构中最大单元承载比;rkmin为结构中最小单元承载比;dk为承载比均匀度;NM为网格划分单元总数。 (16) (17) 重复以上计算过程,直到两相邻迭代步的极限承载力满足以下收敛准则。 (18) 式中:ε为收敛容差,作为收敛的判据,通常取值为0.001~0.01,本文取0.001。 如果第M次迭代满足式(18)的收敛准则时,则该结构的极限承载力PL为 (19) 弹性模量缩减法从建模到迭代分析,只涉及到钢管混凝土合成本构关系中的线弹性段,而且整个计算过程属于线弹性迭代分析,不涉及材料非线性行为,从而保证了迭代计算过程的稳定性和高效率。同时,由于钢管混凝土构件承载力相关方程建立在试验研究基础上,能够真实反映钢管混凝土构件受力变形特性,因此通过单元承载比建立的钢管混凝土拱极限承载力分析格式能够合理体现钢—混凝土协调变形模式。 文献[2]给出了2个抛物线钢管混凝土模型拱,拱轴线方程均为y=x2/3.45,跨度为4.6 m,矢跨比为0.33,在两模型拱的拱顶和四分点分别作用集中力,如图4所示。钢管混凝土外直径D=76 mm,钢管厚度t=3.792 mm,钢材屈服强度fy=307.67 MPa,弹性模量Es=206GPa;混凝土立方体抗压强度fcu=36.8 MPa,弹性模量Ec=31 GPa。 图4 抛物线深拱计算模型 首先,分析有限元网格划分单元总数NM对弹性模量缩减法计算结果的影响。以拱桥规范给出的稳定系数为例,极限承载力结果见表2。 表2 划分不同网格下弹性模量缩减法的极限承载力结果 kN 由表2可知,对于拱顶和四分点加载2种不同的荷载工况,将钢管混凝土模型拱离散为16个单元时,均可以得到稳定收敛的计算结果。 其次,分析不同的稳定系数表达式对稳定极限承载力结果的影响,见表3。 表3 稳定系数对极限承载力计算结果的影响 kN 由表3可知,对于单点加载矢跨比为0.33的深拱而言,不同公式定义的稳定系数的计算结果差别不大,与试验值相比误差均不超过5%,其中式(5)的计算精度最高,最大误差仅为1.1%。 进一步地,结合式(5)的稳定系数表达式,分析广义屈服函数与齐次广义屈服函数对弹性模量缩减法计算结果的影响,如图5所示,图中GYF和HGYF分别代表广义屈服函数和齐次广义屈服函数。从图5中可知,采用广义屈服函数时,拱桥稳定极限承载力计算结果随荷载基准值P0的改变而发生明显变化,严重影响到计算精度和结果的稳定性。而当采用齐次广义屈服函数分析时,弹性模量缩减法计算结果稳定,不受荷载基准值的影响,且具有较高的计算精度。 图5 极限承载力迭代过程图 将本文方法获得的计算结果与增量非线性有限元法进行对比,见表4。其中文献[6]和文献[7]采用纤维单元建立计算模型;文献[2]给出了2种模型,其一是利用双材料梁单元(即钢管梁单元和混凝土梁单元)建立计算模型(见表4中的文献[2]-1),其二是利用单一组合材料梁单元建立计算模型(见表4中的文献[2]-2)。从表4可以看出:采用不同的单元模型对增量非线性有限元法的计算结果有较大影响:单一组合材料梁单元计算结果的最大误差达到18.6%,双材料梁单元的计算结果的最大误差也达到10%;纤维单元计算结果的最大误差为6.7%,而且采用纤维单元时增量非线性有限元法计算模型的离散未知量非常大,从而导致增量非线性有限元法迭代计算耗时久,一个简单的钢管混凝土模型拱的计算有时需要长达10余小时[2]。与此形成对比的是,本文基于弹性模量缩减法建立的线弹性迭代方法最大误差为1.1%。利用CPU为2.90 GHz、内存为1.93 GB的普通台式电脑,其计算耗时不超过25 s。充分证明了本文方法具有较高的计算精度和效率。 表4 结构极限承载力分析结果 kN 导致上述结果的原因在于钢管混凝土材料弹塑性本构模型会直接影响到增量非线性有限元法的计算精度。由于迄今为止尚没有建立适用于复杂受力条件下弹塑性分析的钢管混凝土组合材料合成本构关系,导致基于单一组合材料梁单元的增量非线性有限元法计算结果精度欠佳,而双材料梁单元由于无法精细模拟钢管和混凝土之间的相互作用以及混凝土脱空的影响,同时也难以考虑混凝土开裂对钢管混凝土受力性能的影响[2],因此计算精度也不理想。另外,纤维模型需要通过迭代分析确定截面刚度,理论复杂,同时需要将钢管混凝土截面离散为大量纤维块,将导致增量非线性有限元法迭代计算量大、耗时久。 本文方法采用齐次广义屈服函数定义钢管混凝土截面上的单元承载比,能够合理体现截面上不同材料纤维之间的协调变形特性和的自适应调整能力,减少人为干扰,且大幅降低离散未知量。同时在整个迭代计算过程中本文方法只用到钢管混凝土的线弹性本构方程,因此能够取得远高于增量非线性有限元法的计算效率、计算精度和迭代稳定性。 文献[2]给出了1个钢管混凝土模型拱,轴线方程为y=x2/9.375,跨度为7.5 m,矢跨比为0.2,在模型拱2L/3和5L/6处分别作用一集中力,如图6所示。钢管混凝土外直径D=121 mm,钢管厚度t=4.5 mm,屈服强度fy=245 MPa,弹性模量Es=180 GPa;混凝土立方体抗压强度fcu=25.2 MPa,弹性模量Ec=30 GPa。 首先,分析有限元离散网格对弹性模量缩减法计算结果的影响,同样以拱桥规范给出的稳定系数为例,结果见表5。 图6 抛物线深拱计算模型 由表5可知,对于该两点非对称加载工况,将钢管混凝土模型拱离散为24个单元时,可以得到稳定收敛的计算结果。 其次,分析不同的稳定系数表达式对稳定极限承载力结果的影响,见表6。 表6 稳定系数对极限承载力计算结果的影响 kN 由表6的计算结果可知,对于两点非对称加载矢跨比为0.2的深拱而言,不同公式定义的稳定系数计算结果差别不大,与试验值相比误差均在10%之内,其中式(5)和式(6)的计算误差分别为8.9%和7.0%,均具有较高的计算精度。采用与算例1相同的PC机,计算耗时为21.8 s,表明本文方法具有较高的计算效率。 最后,结合式(5)稳定系数表达式,分析广义屈服函数与齐次广义屈服函数对弹性模量缩减法计算结果的影响,如图7所示。由图7可知,采用广义屈服函数分析时,拱桥稳定极限承载力的计算结果随着荷载初始值的取值不同而出现明显变化,严重影响到弹性模量缩减法的计算精度和稳定性。而当采用齐次广义屈服函数时,弹性模量缩减法计算结果稳定,不受初始荷载的影响。 图7 极限承载力迭代过程图 文献[3]进行了2个抛物线钢管混凝土浅拱模型试验,其中一个模型拱的轴线方程为y=x2/20.25,跨度为9.0 m,矢跨比为1/9,在拱顶处作用集中力,如图8(a)所示。另一个模型拱的轴线方程为y=x2/13.50,跨度为9.0 m,矢跨比为1/6,在四分点处作用集中力,如图8(b)所示。2个模型拱的截面尺寸与材料参数相同,其中钢管外直径D=159 mm,钢管厚度t=4.5 mm,钢材屈服强度fy=376.2 MPa,弹性模量Es=204 GPa;混凝土立方体抗压强度fcu=41.6 MPa,弹性模量Ec=31.3 GPa。 图8 抛物线浅拱计算模型 首先,分析有限元离散网格对弹性模量缩减法计算结果的影响,以拱桥规范给出的稳定系数为例,结果见表7。 由表7可知,对于拱顶和四分点加载2种不同的荷载工况,将模型拱离散为24个单元时,均可以得到稳定收敛的计算结果。 表7 划分不同网格下弹性模量缩减法的极限承载力结果 kN 其次,分析不同的稳定系数表达式对稳定极限承载力结果的影响,结果见表8。 表8 稳定系数对极限承载力计算结果的影响 kN 由表8可知,对于拱顶加载矢跨比为1/9和四分点加载矢跨比为1/6的浅拱2种工况,不同稳定系数表达式下的稳定极限承载力计算结果有一定差异。当拱顶加载矢跨比为1/9时,与试验值相比,式(2)计算精度最高,误差不足1.0%,而式(6)误差则达到7.8%;当四分点加载矢跨比为1/6时,刚好相反,式(6)计算精度最高,误差为4.3%,而式(2)精度最差,误差为6.5%。相比之下,式(5)在2种工况下的误差分别是2.6%和5.4%,均能取得良好的计算精度,稳定性较强,同时采用与算例1相同的PC机计算耗时分别为25.7和28.2 s,表明本文方法具有较高的计算效率。 最后,结合式(5)稳定系数表达式,再一次分析广义屈服函数与齐次广义屈服函数对弹性模量缩减法计算结果的影响,如图9所示。由图9可知,采用广义屈服函数进行分析时,拱桥稳定极限承载力的计算结果随荷载初始值改变而呈现明显变化,严重影响到弹性模量缩减法计算精度和稳定性。而当采用齐次广义屈服函数时,弹性模量缩减法计算结果稳定,不受初始荷载的影响。 综合以上3个算例计算结果和误差分析可知,常用的3种稳定系数表达式的计算误差均不超过10%,都能够满足工程实践要求,其中钢管混凝土拱桥规范建议的稳定系数表达式(5)在不同荷载工况、不同矢跨比情况下具有更好的稳定性与良好的计算精度。 图9 极限承载力迭代过程图 (1)本文建立的钢管混凝土构件压弯稳定分析的齐次广义屈服函数克服了广义屈服函数受荷载初始值和钢管混凝土截面几何参数、材料参数影响的缺陷,具有较强的适用性。 (2)本文方法克服了钢管混凝土抛物线拱结构稳定承载力分析的增量非线性有限元法的缺陷,具有较高的计算精度和效率。 (3)当前常用的3种稳定系数表达式都能够取得满意的计算精度,其中钢管混凝土拱桥规范建议的稳定系数表达式具有更好的稳定性与良好的计算精度。 [1]徐勇,马庭林,陈克坚. 水柏铁路北盘江大桥钢管混凝土拱设计[J]. 中国铁道科学, 2003, 24(5): 35-40. (XU Yong, MA Tinglin, CHEN Kejian. Steel Tube with Concrete Filling Arch Design of Beipanjiang Large Bridge[J]. China Railway Science, 2003, 24(5): 35-40. in Chinese) [2]陈宝春. 钢管混凝土拱桥[M]. 北京: 人民交通出版社, 2007: 135, 719-757. [3]LIU C Y, WANG Y Y, WU X R, et al. In-Plane Stability of Fixed Concrete-Filled Steel Tubular Parabolic Arches under Combined Bending and Compression[J]. Journal of Bridge Engineering, 2016, 22(2): 4016116. [4]韦建刚,陈宝春,吴庆雄. 钢管混凝土压弯拱非线性临界荷载计算的等效梁柱法[J]. 工程力学, 2010, 27(10): 104-109. (WEI Jiangang, CHEN Baochun, WU Qingxiong. Equivalent Beam-Column Method to Calculate Nonlinear Critical Load for CFST Arch under Compression and Bending [J]. Engineering Mechanics, 2010, 27(10): 104-109. in Chinese) [5]WU X R,LIU C Y,WANG W, et al. In-Plane Strength and Design of Fixed Concrete-Filled Steel Tubular Parabolic Arches[J]. Journal of Bridge Engineering, 2015, 20(12): 4015016. [6]邓继华,周福霖,谭平. 圆钢管混凝土拱空间极限荷载计算方法研究[J]. 建筑结构学报, 2014, 35(11): 28-35. (DENG Jihua, ZHOU Fulin, TAN Ping. Study on Method for Calculating Spatial Ultimate Load of Circular CFST Arch [J]. Journal of Building Structures, 2014, 35(11): 28-35. in Chinese) [7]丁发兴,余志武,蒋丽忠. 圆钢管混凝土结构非线性有限元分析[J]. 建筑结构学报, 2006, 27(4): 110-115. (DING Faxing, YU Zhiwu, JIANG Lizhong. Nonlinear Finite Element Analysis of Concrete Filled Circular Steel Tubular Structures [J]. Journal of Building Structures, 2006, 27(4): 110-115. in Chinese) [8]钟善桐. 钢管混凝土统一理论: 研究与应用[M]. 北京: 清华大学出版社, 2006: 99-101. [9]SESHADRI R, HOSSAIN M M. Simplified Limit Load Determination Using theMα-Tangent Method[J]. Journal of Pressure Vessel Technology, 2009, 131(2): 021213. [10]MACKENZIE D, BOYLE J T. Elastic Compensation Method for Limit and Shakedown Analysis: a Review[J]. Journal of Strain Analysis for Engineering Design, 2000, 35(3): 171-188. [11]YANG L F, YU B, JU J W. Incorporated Strength Capacity Technique for Limit Load Evaluation of Trusses and Framed Structures under Constant Loading[J]. Journal of Structural Engineering, 2015, 141(11): 4015023. [12]YANG LF, LI Q, ZHANG W, et al. Homogeneous Generalized Yield Criterion Based Elastic Modulus Reduction Method for Limit Analysis of Thin-Walled Structures with Angle Steel[J]. Thin-Walled Structures, 2014, 80(9): 153-158. [13]HAMILTON R, BOYLE J. Simplified Lower Bound Limit Analysis of Transversely Loaded Thin Plates Using Generalised Yield Criteria[J]. Thin-Walled Structures, 2002, 40(6): 503-522. [14]钟善桐. 钢管混凝土结构[M]. 哈尔滨: 科学技术出版社, 1994: 281-284. (ZHONG Shantong. Concrete Filled Steel Tubelar Structures [M]. Harbin:Heilongjiang Science and Technology Press,1994:281-284. in Chinese) [15]蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2003: 74-75,152-153. (CAI Shaohuai. Modern Steel Tube Confined Concrete Structures[M].Beijing: China Communications Press,2003:74-75,152-153. in Chinese) [16]LEE S H, UY B, KIM SH, et al. Behavior of High-Strength Circular Concrete-Filled Steel Tubular (CFST) Column under Eccentric Loading[J]. Journal of Constructional Steel Research, 2011, 67(1): 1-13.1.4 广义屈服函数齐次化

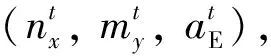
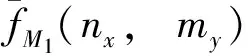


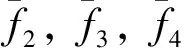
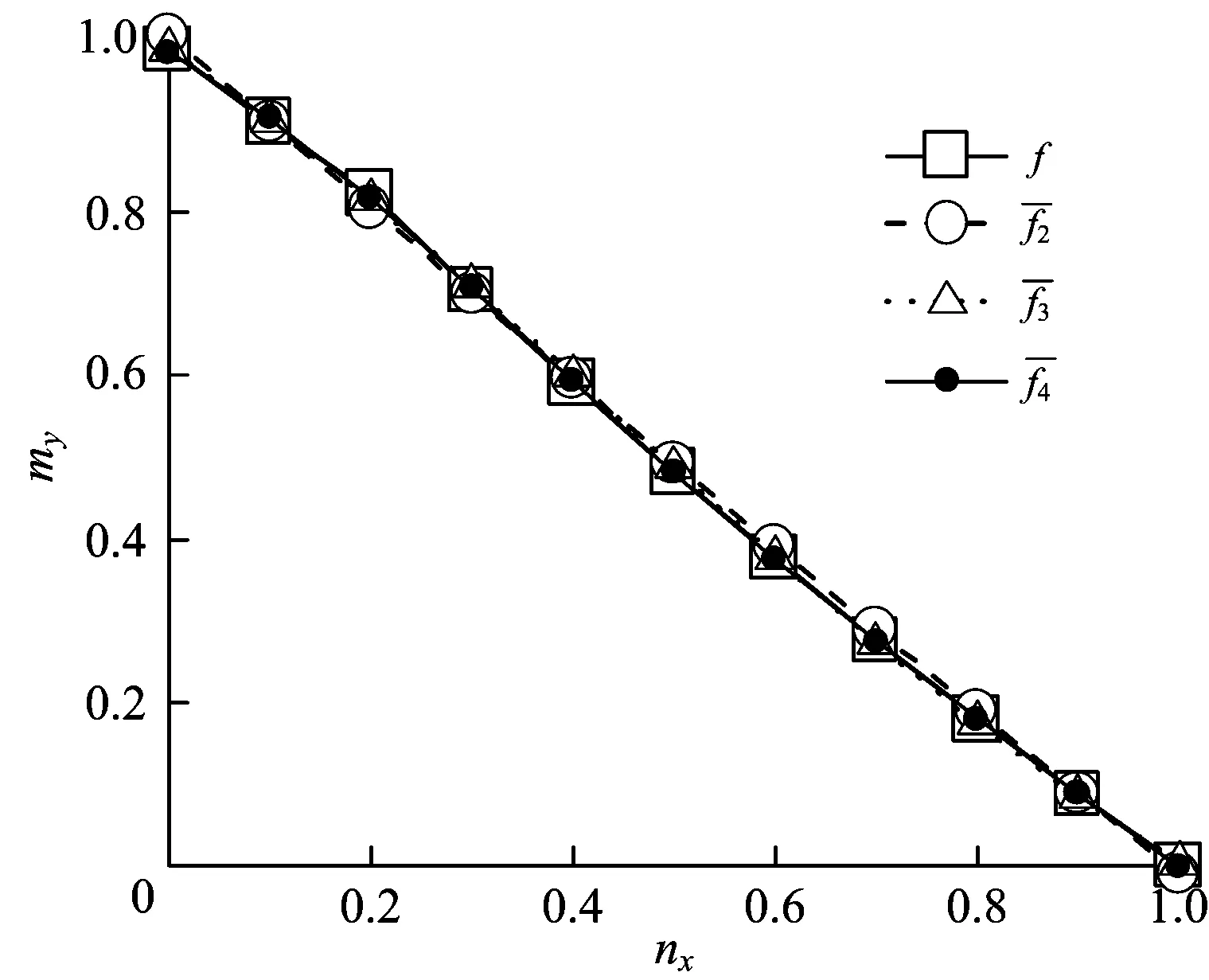
1.5 齐次广义屈服函数的准确性验证


2 钢管混凝土拱桥稳定极限承载力


3 算例分析及验证
3.1 拱顶和四分点加载抛物线钢管混凝土深拱



3.2 两点非对称加载抛物线钢管混凝土深拱


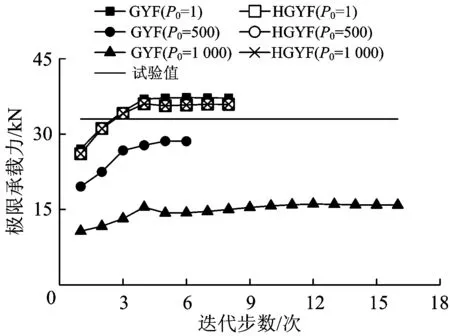
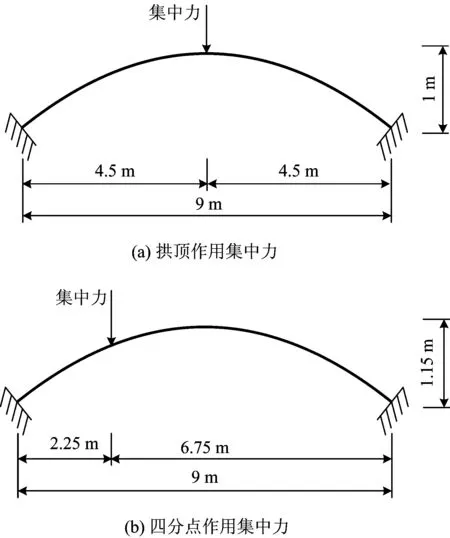
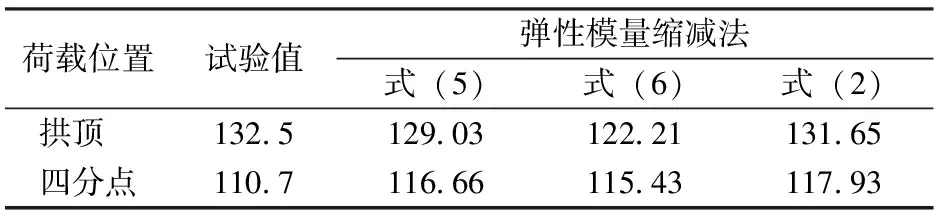
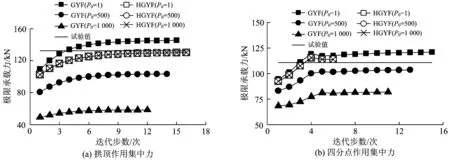
3.3 拱顶和四分点加载抛物线钢管混凝土浅拱

4 结 论

