通用航空机队设备可靠性动态识别模型

陈勇刚，熊升华，贺强，贺元骅

中国民用航空飞行学院 民航安全工程学院，广汉 618307

通用航空与运输航空是民航行业的两翼，随着中国低空空域的逐步开放，通用航空将迎来快速发展时期，通用航空机队规模将得到前所未有的加速增长态势[1]。近几年，通用航空企业在册航空器总数年均递增超10%，据预测到2020年，通用航空机队规模将近4 000架左右[2]。由此带来的通用航空机队设备可靠性管理问题将进一步突出。通用航空机队设备可靠性不仅仅涉及到通航企业运行过程中的安全性和经济性，同时也是决定通航飞机效能和寿命周期费用的重要因素，更是通航继续可持续健康发展的重要保障。然而，通用航空机队可靠性管理工作在中国民航规章中并没有明确规定，绝大多数都还是借鉴运输航空来执行的，还未针对通用航空特点形成“以可靠性为中心”的维修数据管理模式，通用航空机队设备可靠性状态分析技术手段还比较薄弱[3]。通用航空机队设备可靠性状态识别是实现可靠性状态的动态监控和系统性分析的关键技术，为通航机务部门科学开展可靠性管理工作和消除机队设备安全隐患和缺陷提供科学依据。

目前国内外航空设备可靠性研究主要集中在：① 可靠性数据的统计分析，如航空电子产品可靠性BAYES统计推断[4];② 产品部件及其系统可靠性分析，如文献[5]飞机部件可靠性非参数统计分析方法等；③ 可靠性与维修性，如文献[6]阐述了航空装备可靠性和维修性要求的确定与分配，可靠性、维修性预计以及试验与验证等理论；④ 可靠性质量标准，如复杂通用航空器运行可靠性基准[7]；⑤ 可靠性评估方法与模型，如航空发动机可靠性指标评估方法、航空公司机队设备可靠性非线性动态评估模型、航空装备现场数据可靠性评估方法有效性分析[8-10]。国内外学者在航空设备可靠性相关问题上有了一系列的研究成果，但在通用航空机队设备可靠性领域的研究甚少，尚未形成一套针对于通航运行特点的机队设备可靠性动态识别方法。因此，为满足通用航空机队设备可靠性状态评估的需要，迫切需要将可靠性识别方法进一步深入研究。

通用航空机队设备可靠性状态容易受到人员、飞机类型，飞机役龄、生产环境、自然环境和组织安全管理等诸多变化因素的影响，具有随机性、波动性、模糊性、不确定性等多重特征。权重阶梯朴素贝叶斯分类器能够较好地解决随机性、波动性、非线性和多指标等复杂问题，实现动态评估。同时，该方法基于客观获取的指标权重信息构建分类器的结构，能够有效地反映指标间的内在联系。此外，随着训练样本的不断增加，权重阶梯朴素贝叶斯分类器的结构、状态级别的先验概率以及相应的条件概率将逐渐趋于稳定，有助于提升状态识别结果的合理性。因此，权重阶梯朴素贝叶斯分类器为确定通用航空机队可靠性状态评估提供了一种可行且合理的新方法。本文将运用该方法，构建通用航空机队可靠性状态评估模型，在结合理论分析和通用航空机队安全管理工作实际情况的基础上，对通用航空机队可靠性状态进行实例分析。通过科学有效的机队可靠性状态分析，可以保障飞行安全、降低维修成本，以期实现安全和生产、安全和效益的辩证统一。

1 机队可靠性指标确定

通用航空机队设备可靠性评估的前提是对可靠性指标进行选取，可靠性指标的选取直接影响评估结果。而指标选取的关键要素就是需要选取的指标能够直接反映机队设备在日常运行维护中的具体状态，同时需要具备可获取性、可衡量性和可监控性。选取时应包括设备在设计过程中确定的参数与维护使用过程中的可靠性参数。总而言之，通用航空机队设备可靠性指标应包括飞机的固有性、使用性和维修性等内容。

通用航空单位不同于运输航空，一般来说通用航空企业规模都比较小，运行标准略低于运输航空，机队机型简单，在数据采集方面，能采取到的数据也有一定限制。当下大部分的通航企业都会根据自身的单位机队的组成情况，收集与机队相适应的可靠性数据，从而有针对性地进行可靠性管理。所以，在指标的选取上应综合考虑通用航空机队可靠性数据收集和统计的便利性，本文采用ATA100章节名称作为指标源，结合对管理人员、技术人员的调查与访谈意见以及现场实际应用情况，最终得到通用航空机队设备可靠性指标为：通讯X1、电源X2、飞行操纵X3、燃油X4、起落架X5、灯光X6、导航X7、动力装置X8、发动机燃油控制X9、点火X10、发动机指示X11、设备装饰X12、润滑X13和真空X14。其中Xi(i=1,2,…,14)表示故障数。

2 可变模糊模式识别模型

2.1 熵权法确定指标权重

传统确定权重的德尔菲法、专家调查法和层次分析法等，在确定权重时常常伴随有人的主观性判断，导致结果客观性下降。熵权法是利用信息效用值来计算各指标权重的一种客观的赋权方法，可有效消除人的主观性带来的偏差。

假设识别样本组成的指标特征值矩阵为X，其由m个指标和n个样本构成。

熵权法确定权重步骤如下[11]：

步骤1数据无量纲化处理

(1)

式中：pij为去量纲化指标特征值，0≤pij≤1；xij为第j个样本第i个指标的样本值;xjmin为指标特征值矩阵X中第j个指标所对应的最小值；xjmax为指标特征值矩阵X中第j个指标所对应的最大值。

步骤2计算熵值

(2)

(3)

步骤3计算指标的熵权向量w

(4)

2.2 可变模糊模式识别模型

设指标标准值矩阵为Y，表示按照各指标的l个级别进行识别获得的标准值矩阵。指标分为递增型和递减型2类，对应的处理公式也有所不同，在进行模糊识别时必须先对X和Y进行规格化处理，则得到规格化矩阵R和S。进行规格化处理的公式为[12]：

1) 极大型指标(越大越优)

(5)

(6)

2) 极小型指标(越小越优)

(7)

(8)

式中：yi1、yih和yil分别为指标i的第1级、第h级和第l级标准值；rij为样本j对应指标i规格化值；sih为级别h对应指标i的规格化值。

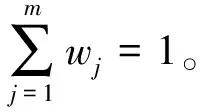
首先，计算相对隶属度矩阵U=[uhj]l×n。

(9)

式中：a为优化标准参数，a=1为最小一乘方准则，a=2为最小二乘方准则；p为距离参数，p=1为海明距离，p=2为欧式距离。a、p称为可变模糊模型参数，通常有4种组合：a=1、p=1；a=1、p=2；a=2、p=1；a=2、p=2。若未作特殊说明，本文选取a=2、p=2进行计算。

而aj和bj分别为第j个样本的级别下限值和上限值[13]。

随后，应用级别特征值模型

Hj=[1,2,…,l]·uj

(10)

其中:uj=[u1j,u2j,…,ulj]T。

最后，结合判断准则

对模糊识别模型结果进行级别判断。

3 权重阶梯朴素贝叶斯分类器模型

贝叶斯分类器的实质为，将指标结点作为证据结点引入到贝叶斯网络中，并求得待分类对象隶属于各类结点的后验概率。同时，令最大后验概率所对应的类别结点为该对象所属的类别[14]。鉴于学习无任何限制条件的贝叶斯网络的时间复杂度为指标变量的指数级，大量的限制性贝叶斯分类器被提出。其中，具有代表性的2种是朴素贝叶斯分类器[15]和树形增强朴素贝叶斯(Tree-Augmented Naive Bayesian, TAN)分类器[16]。朴素贝叶斯分类器假设各指标节点仅与类节点相关，而指标间彼此相互独立，从而简化其复杂度。尽管相关文献已验证基于该假设下的分类效果十分优良，但该假设通常与实际不符。针对该问题，Friedman等[16]弱化了朴素贝叶斯分类器中“指标间相互独立”的条件，并假设指标间有且仅有一条关系链，提出了分类效果更好的TAN分类器。基于TAN分类器的思想，本文考虑指标重要程度的差异，提出权重阶梯朴素贝叶斯分类器。

3.1 权重阶梯朴素贝叶斯分类器的构造

步骤1输入训练集A={A1,A2,…,Am}。

步骤2构建类节点C={c1,c2,…,cl}与指标节点X={X1,X2,…,Xn}的权重阶梯树。

1) 根据训练集的指标特征值矩阵X，用2.1节中的熵权法确定各指标的权重所构成的集合W={w1,w2,…,wn}。

2) 令有向边的条数i=1。

3) 在集合W中选取最大的2个权重(即max(W)和max(W(max(W))))，并利用它们所对应的指标构建第i条有向边。其中，权重较大者作为父节点，权重较小者作为子节点。

4) 令权重集合W=W(max(W))，有向边的条数i=i+1。

5) 重复3)和4)，直至i=n。

步骤3增加类节点到所有指标节点的有向边。

步骤4学习参数并输出权重阶梯朴素贝叶斯分类器。

本文根据训练集的指标特征值矩阵X，利用第2节给出的可变模糊模式识别模型获取输入训练集A={A1,A2,…,Am}。易知，在权重阶梯朴素贝叶斯分类器中，每个指标不但拥有类节点作为父节点，而且可以拥有至多一个其他指标节点作为父节点。图1给出了包含4个指标的权重阶梯朴素贝叶斯分类器示意图。由图1知，各指标的权重大小排序为w1≥w2≥w3≥w4。

3.2 权重阶梯朴素贝叶斯分类器的分类方法

根据贝叶斯公式

(11)

计算待分类的输入(x1,x2,…,xn)的后验概率P(cj|x1,x2,…,xn)(cj∈C)。则最大后验概率所对应的类标签c*为待分类输入所属的类别，即[14]

(12)

式中：Pai为指标Xi(i=1,2,…,n)的所有父节点构成的集合。在式(12)中，为了避免先验概率P(cj)(cj∈C)和条件概率P(xi|Pai)(i=1,2,…,n)值为“0”情形，引入拉普拉斯平滑参数[14]，并利用式(13)进行计算。

(13)

式中：N为样本的总数量；Ncj为归属于cj类的样本数量；K为类别数量，λ(0≤λ≤1)为拉普拉斯平滑参数，通常取λ=1。条件概率可类似地计算为

(14)

式中：Nxi,Pai为指标Xi下值为xi且指标Xi的父节点为Pai中对应值的样本数量；NPai为指标Xi的父节点为Pai中对应值的样本数量；Li为样本集中指标Xi下的取值个数[14]。

由于指标的权重是由样本数据客观获取，因而客观地反映着指标间的相关关系。依据权重大小构建权重阶梯树旨在反映主要指标关系的同时，保持与增强型朴素贝叶斯分类器相同的计算复杂度。此外，本文提出的权重阶梯朴素贝叶斯分类器弱化了朴素贝叶斯分类器中“指标间相互独立”的条件，并假设指标间有且仅有一条关系链，因而更具合理性。

4 应用实例

机队设备可靠性是用来反映机队运行安全的可衡量、可控制的总体指标，包括通讯、电源、飞行操纵、燃油、起落架、灯光、导航、动力装置、发动机燃油控制、点火等诸多因素，本文选取某通航运行单位2012～2015年塞斯纳172R飞机故障统计数据进行机队设备可靠性状态识别。通过选取每100架172R飞机月发生故障数进行分析处理，得到的通用航空机队设备可靠性数据如表1所示。

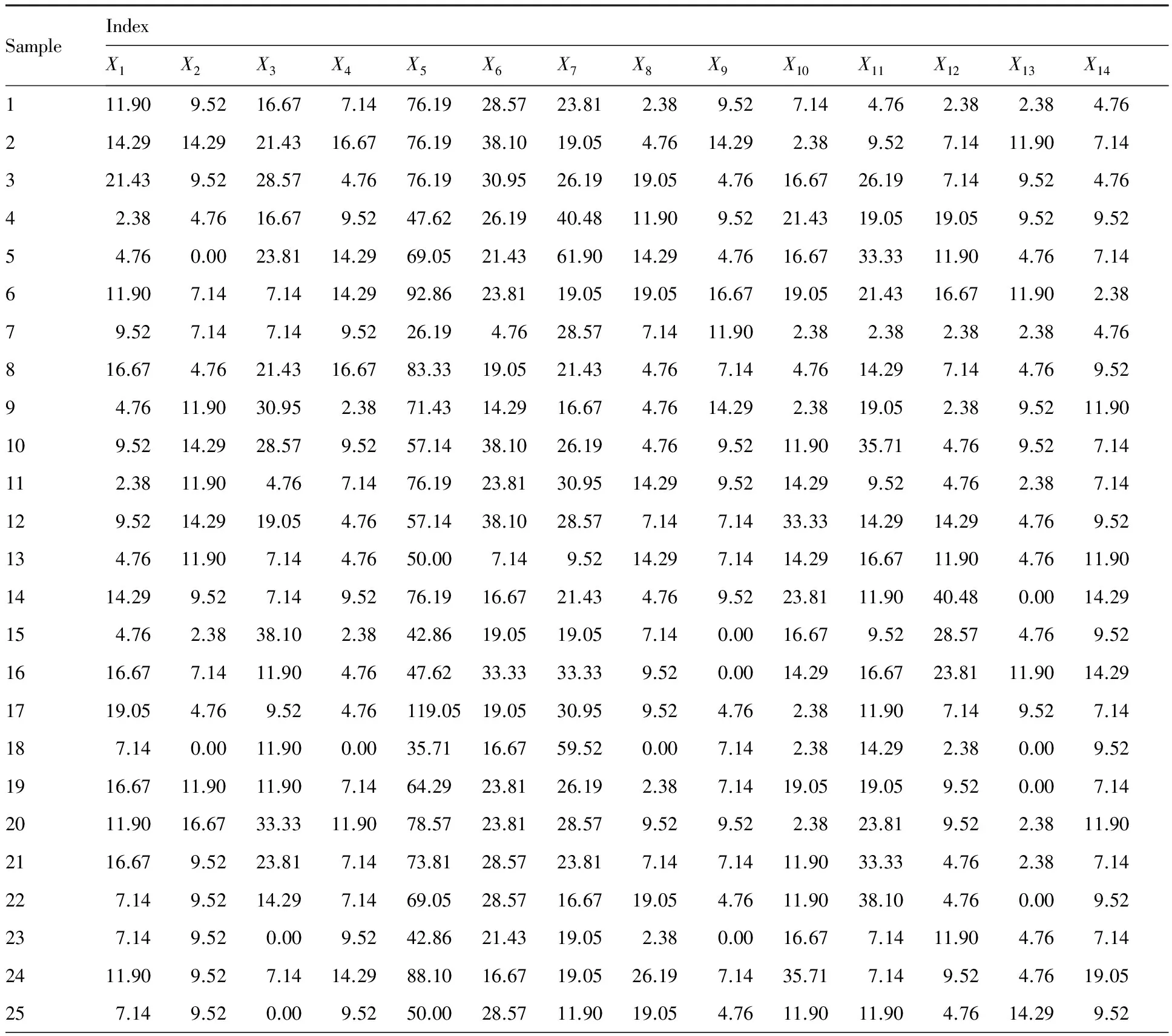
表1 通用航空机队设备可靠性数据Table 1 Reliability data of general aviation fleet equipment

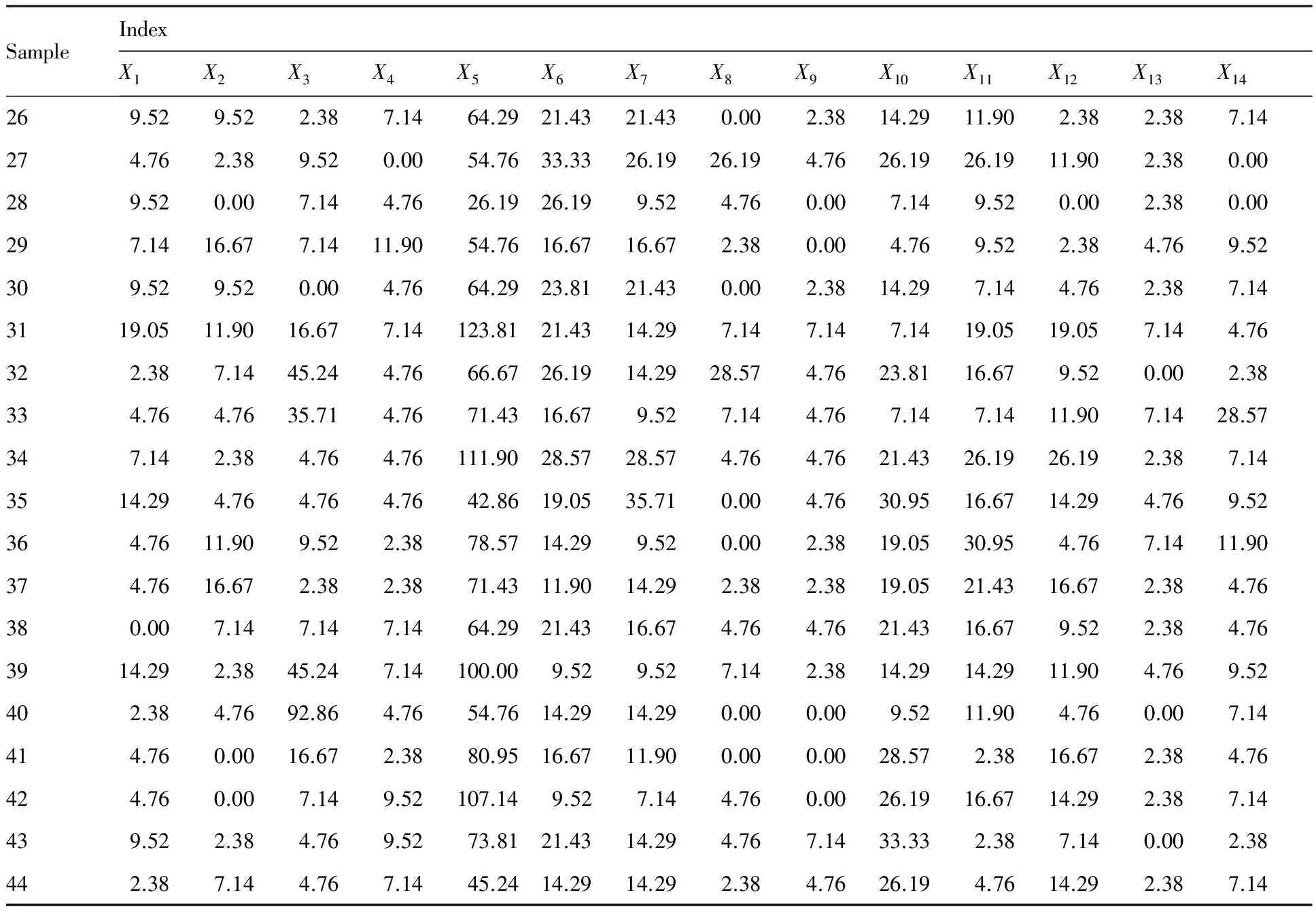
续表

4.1 通用航空机队设备可靠性等级标准划分

根据表1的实际数据信息，绘制各组数据频数直方图和频率分布直方图，按照绘制图形规律将通用航空机队设备可靠性评价指标标准分为5个等级，即可靠性高(Ⅰ)、较高(Ⅱ)、一般(Ⅲ)、较低(Ⅳ)和低(Ⅴ)。其中前2级表示机队可靠性合格，不会影响机队运行；可靠性一般(Ⅲ)表示在合理检查的情况下，在一定程度上是可靠的，但仍需注意；后2级表示可靠性不高，需要重新进行检修。通用航空机队设备可靠性评价指标分级标准如表2所示。

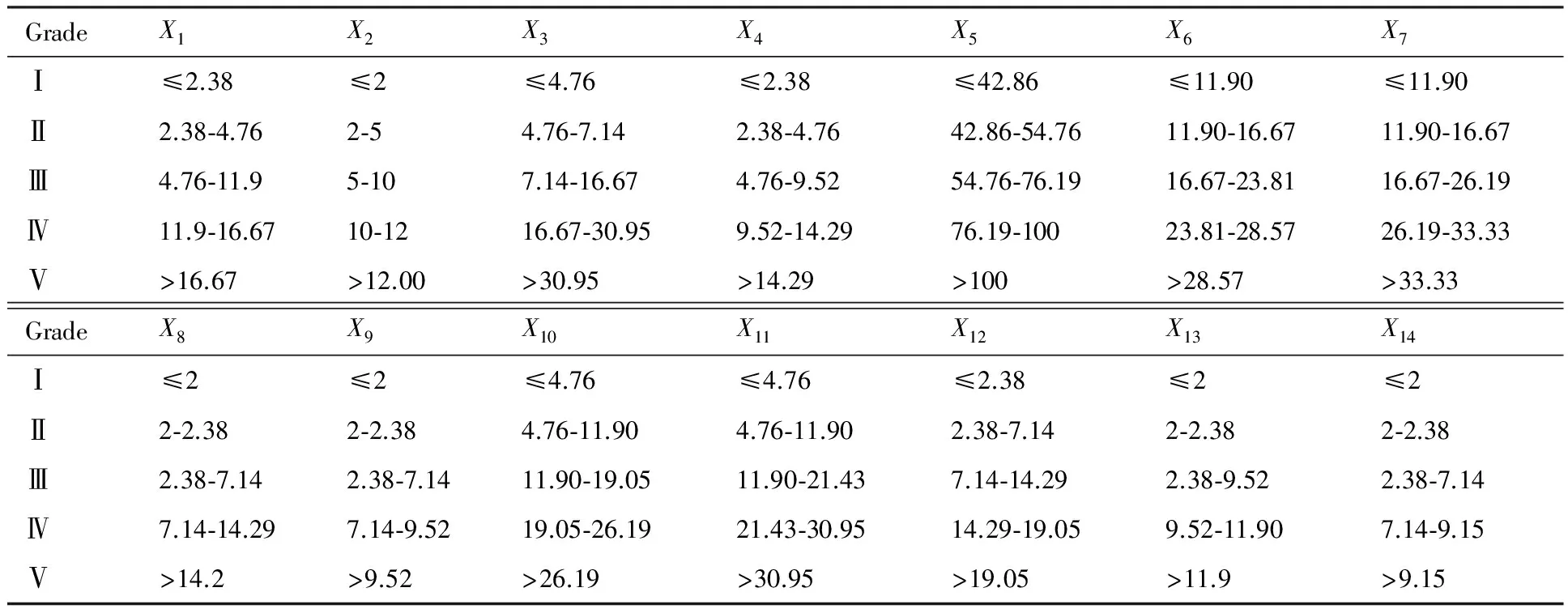
表2 通用航空机队设备可靠性评价指标分级标准Table 2 Evaluation index classification standard for reliability of general aviation fleet equipment

4.2 通用航空机队可靠性可变模糊模式识别

根据表1和表2，本文选取前41个样本作为训练样本，样本42和样本43作为检验样本，样本44作为待识别样本。首先将各指标测度值进行无量纲化处理。由式(8)可求得指标标准的规格化矩阵为

S=

由式(7)可类似地获得通用航空机队可靠性的规格化矩阵R=[rij]41×14，限于篇幅，此处省略详细数据。

随后，依据2.1节给出的熵权法确定指标的权重为

w=[0.071 8,0.088 2,0.052 0,0.071 0,0.058 3,

0.058 6,0.068 6,0.098 2,0.080 7,0.088 1,

0.075 3,0.058 5,0.090 8,0.039 8]T

(15)

然后，根据式(9)，计算各样本的相对隶属度，得到相对隶属度矩阵U。

最后，根据级别特征值式(10)对模糊识别模型进行计算，并根据各Hj(j=1,2,…,10)的值结合判断准则对通用航空机队可靠性进行评价，状态识别结果如表3所示。依据表1和表2，表3还给出了训练样本在各指标下的评价值所归属的级别。

4.3 构建权重阶梯朴素贝叶斯分类器

由熵权法获得的指标权重知，各指标的权重大小排序为

w8>w13>w2>w10>w9>w11>w1>

w4>w7>w6>w12>w5>w3>w14

因而构建的通用航空机队可靠性权重阶梯朴素贝叶斯分类器如图2所示。

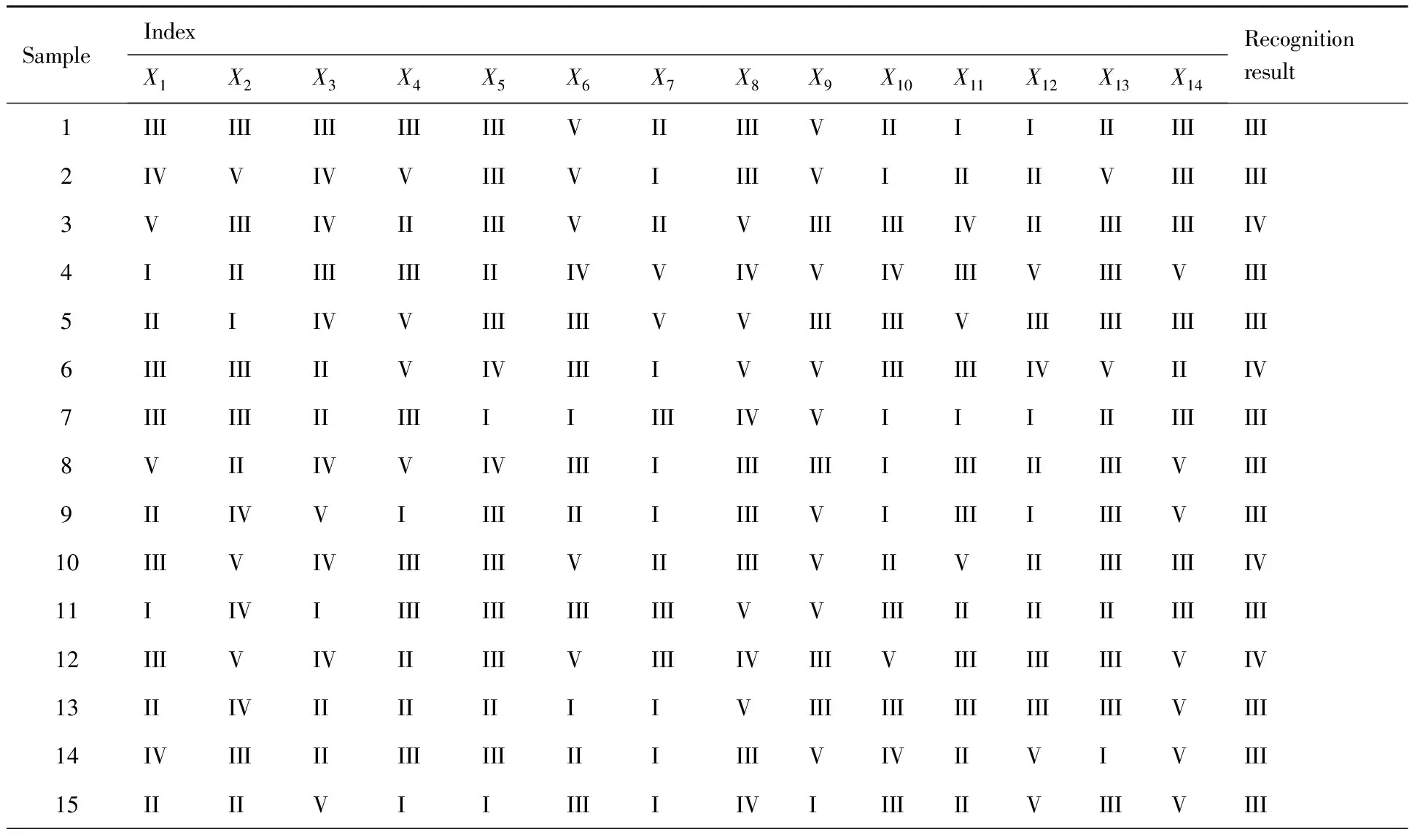
表3 通用航空机队可靠性状态识别结果Table 3 Reliability recognition results of general aviation fleet equipment

续表

4.4 权重阶梯朴素贝叶斯分类器可靠性状态识别

基于图2所示通用航空机队可靠性权重阶梯朴素贝叶斯分类器，利用式(12)～式(14)和表3的数据，测试样本和待识别样本的可靠性状态识别结果如表4所示。其中：

cj∈C

需指出的是，在利用权重阶梯朴素贝叶斯分类器进行可靠性状态识别时，样本关于可靠性状态cj∈C的后验概率由式(16)计算得到

(16)

4.5 对比分析

为便于比较，表5给出了测试样本42和样本43在可变模糊识别模型和树形增强朴素贝叶斯分类器[16]下的可靠性状态识别结果。其中，可变模糊识别模型的识别结果基于式(15)所示的属性权重计算而得到。而在利用树形增强朴素贝叶斯分类器对通用航空机队可靠性状态识别的过程中，根据文献[16]，首先,基于式(17)计算指标Xi和Xj(i,j=1,2,…,14)的条件互信息。

(17)

表4 通用航空机队测试样本和待识别样本的可靠性状态识别结果Table 4 Reliability recognition results for test samples and sample to be identified of general aviation fleet equipment

一方面，根据通用航空机队可靠性级别特征值识别，结合级别特征值判断准则，表3表明了系统的总体可靠性主要处于Ⅱ级和Ⅲ级之间，因而该通航单位机队可靠性较高。但值得注意的是，样本3、样本6、样本10和样本12的可靠性状态识别结果为第IV级，表明机队安全尚存在少数问题，需要注意排查和加强管理。另一方面，由表4和表5知，权重阶梯朴素贝叶斯分类器对通用航空机队测试样本可靠性状态识别的结果与既有的可变模糊识别方法以及树形增强朴素贝叶斯分类器所得到的结果完全一致，进而表明了本文所提方法的可行性和合理性。此外，对待识别样本的识别结果表明，样本44的可靠性状态为III级，进而说明了该时期是机队设备问题多发期，需要重复检查，以保证机队安全运行。

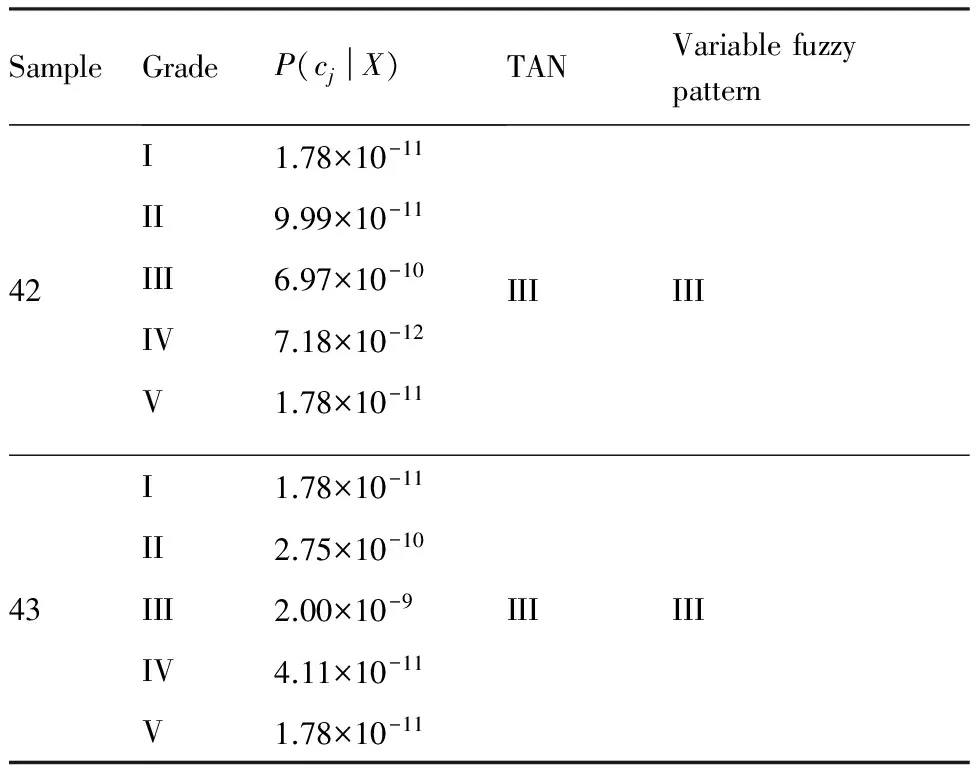
表5 通用航空机队测试样本的可靠性状态识别结果

事实上，相较于传统的通用航空机队可靠性状态识别相关研究而言，基于权重阶梯朴素贝叶斯分类器可靠性状态识别模型优势显著，主要体现在3个方面：① 权重阶梯朴素贝叶斯分类器实质为树形增强朴素贝叶斯分类器的一种变形，进而保证识别方法的可行性；② 异于树形增强朴素贝叶斯分类器关注于指标间的相关程度，权重阶梯朴素贝叶斯分类器旨在反映指标权重大小的关系，且任意指标节点至多是一个其他指标节点的父节点，可有效地反映指标间的内在联系；③ 当训练样本足够大时，权重阶梯朴素贝叶斯分类器结构、状态级别的先验概率以及相应的条件概率将趋于稳定，有助于提升状态识别结果的合理性。

5 结 论

1) 基于权重阶梯朴素贝叶斯分类器的通用航空机队可靠性状态识别模型利用指标权重大小刻画指标间的内在联系，有利于合理构建朴素贝叶斯分类器。

2) 实例和对比分析表明，该模型操作性强、可靠性高、评价结果直观，适用于多指标、多级别的通用航空机队可靠性评估问题。

3) 架构于指标权重大小关系之上的权重阶梯朴素贝叶斯分类器可靠性状态识别模型，能够科学地确定样本关于各评价等级的后验概率，客观地反映评估对象的可靠性等级，实现动态评估。该评估模型丰富了“以可靠性为中心”的维修可靠性数据管理模式，为通用航空机队可靠性状态评估提供了一种新的思路,对于提高航空公司安全水平具有一定的实用价值。

参 考 文 献

[1] 王一姮. 通用航空公司安全运行保障能力模型研究[D]. 天津: 中国民航大学, 2014: 1-2.

WANG Y H. Research on model of safe operation assurance capability of general aviation airline[D]. Tianjin: Civil Aviation University of China, 2014: 1-2 (in Chinese).

[2] 赵琪. 基于灰色预测和OLS的我国通用航空需求预测[J]. 滨州学院学报, 2013, 29(6): 53-57.

ZHAO Q. The forecasting of china’s general aviation demand based on grey prediction model and OLS method[J]. Journal of Binzhou University, 2013, 29(6): 53-57 (in Chinese).

[3] 金肇鹏. 某机型机队可靠性及单机健康状况监控研究[D]. 广汉: 中国民用航空飞行学院, 2011: 4-6.

JIN Z P. A fleet aircraft reliability and single plane health monitoring research[D]. Guanghan: Civil Aviation Flight University of China, 2011: 4-6 (in Chinese).

[4] 张士峰, 蔡洪. 航空电子产品的BAYES可靠性评估[J]. 航天控制, 1999(4): 67-71.

ZHANG S F, CAI H. Bayesian reliability assessment of electronic products in aviation[J]. Aerospace Control, 1999(4): 67-71 (in Chinese).

[5] 王辉, 王龙飞. 基于非参数统计方法的飞机部件可靠性分析[J]. 航空维修与工程, 2012(4): 55-57.

WANG H, WANG L F. Research on aircraft component reliability based on nonparametric statistical methods[J]. Aviation Maintenance & Engineering, 2012(4): 55-57 (in Chinese).

[6] 陈云翔. 可靠性与维修性工程[M]. 北京: 国防工业出版社, 2007: 51-79.

CHEN Y X. Reliability & maintainability engineering[M]. Beijing: National Defend Industry Press, 2007: 51-79 (in Chinese).

[7] DUANCE P, ANDREW T. Study general aviation aircraft reliability: ASA/CR-2001-210647[R]. Washington, D.C.: NASA, 2001.

[8] 王大伟, 王伟, 冯振宇. 基于灰色理论的航空发动机可靠性指标评估方法[J]. 推进技术, 2014, 35(7): 874-881.

WANG D W, WANG W, FENG Z Y. Evaluation method on reliability index of aero-engine based on gray theory[J]. Journal of Propulsion Technology, 2014, 35(7): 874-881 (in Chinese).

[9] 陈勇刚, 罗晓利. 航空公司机队设备可靠性非线性动态评估模型[J]. 航空学报, 2013, 34(1): 104-111.

CHEN Y G, LUO X L. Nonlinear dynamic assessment model of airline fleet equipment reliability[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 104-111 (in Chinese).

[10] 沈安慰, 郭基联, 王卓健. 航空装备现场数据可靠性评估方法有效性分析[J]. 航空学报, 2014, 35(5): 1311-1318.

SHEN A W, GUO J L, WANG Z J. Validity analysis of reliability evaluation method in aviation equipment field data[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1311-1318 (in Chinese).

[11] 陈勇刚, 罗晓利, 杨晓强. 航空公司机队可靠性状态识别方法[J]. 航空学报, 2014, 35(8): 2217-2224.

CHEN Y G, LUO X L, YANG X Q. Recognition method of airline fleet reliability status[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2217-2224 (in Chinese).

[12] 陈守煜, 王子茹, 罗宝力, 等. 可变模糊模式识别方法及在水电站地下厂房岩体稳定性评价中的应用[J]. 水利学报, 2011, 42(4): 396-402.

CHEN S Y, WANG Z R, LUO B L, et al. Method of variable fuzzy pattern recognition and it application to surrounding rock stability of water power station underground building[J]. Journal of Hydraulic Engineering, 2011, 42(4): 396-402 (in Chinese).

[13] 柯丽娜, 王权明, 孙新国, 等. 基于可变模糊识别模型的海水环境质量评价[J]. 生态学报, 2013, 33(6): 1889-1899.

KE L N, WANG Q M, SUN X G, et al. The seawater environment quality evaluation research base on variable fuzzy pattern recognition model[J]. Acta Ecologica Sinica, 2013, 33(6): 1889-1899 (in Chinese).

[14] 蒋良孝. 朴素贝叶斯分类器及其改进算法研究[D]. 武汉: 中国地质大学, 2009: 7-8.

JIANG L X. Research on naive Bayes classifiers and its improved algorithms[D]. Wuhan: China University of Geosciences, 2009: 7-8 (in Chinese).

[15] PEARL J. Probabilistic reasoning in intelligent systems[J]. Computer Science Artificial Intelligence, 1988, 70(2): 1022-1027.

[16] FRIEDMAN N, GEIGER D, GOLDSZMIDT M. Bayesian network classifiers[J]. Machine Learning, 1997, 29(2-3): 131-163.