基于循环相关的雷达信号检测

中国电子科技集团公司第三十九研究所　王小妹　龙甫煜　王永华

1.步进线性调频信号数学模型

步进线性调频信号由多个载频步进的线性调频子脉冲组成，其形式如图1所示。[1]

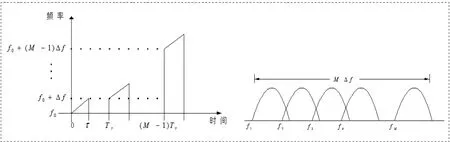
图1　步进线性调频信号时频关系及频谱示意图

步进频率的信号基本思想是：发射一串窄带的脉冲，每个脉冲的载频是均匀步进的。假设一组步进频信号有M个Chirp子脉冲组成，其中第m个子脉冲可写为：

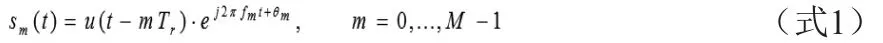
因此总的步进调频信号可以写成：

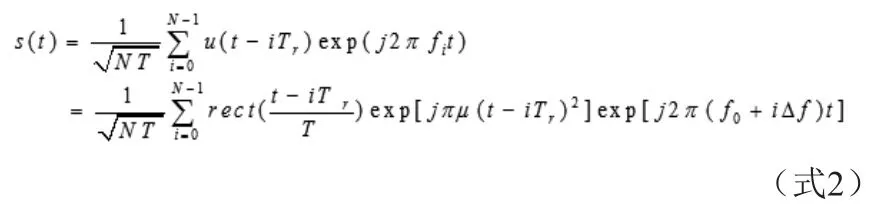
2.步进线性调频信号的相关性

在第m个周期内步进线性调频信号s(t)的瞬时相关函数为[2]：

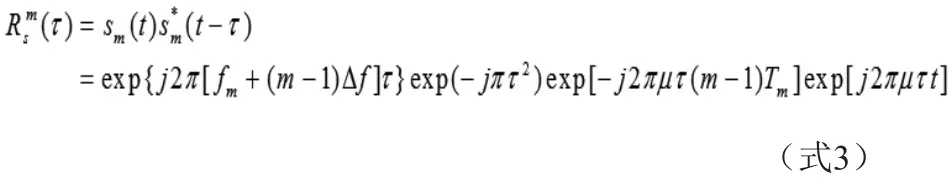
通常情况下， 每个脉冲的载频、周期和调频率相同，因此上式可以写为：

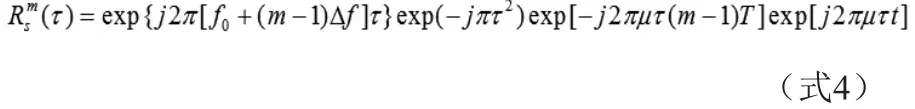
可以看出，在每个脉冲周期内，步进线性调频信号s(t)的瞬时相关函数结果为一个点频信号，这个点频仅仅与调频率μ和相关延迟τ有关。因此，可以用Fourier变换实现信号的最优积累，用于进行信号检测。

3.循环相关算法的形成和噪声特性

步进线性调频信号在一个周期内的瞬时相关函数结果为一个点频信号，因此可以用FFT实现信号的能量最优积累，整个处理过程就是循环自相关算法。

循环自相关定义为：

从统计意义上讲，高斯白噪声在l= 0处相关性最好，当l≠ 0时不相关。在实际中，采用下式：

若l取大于零的常数，由上式可以看出一般情况下噪声的循环自相关函数在零循环频率上有突起的峰。若噪声是白噪声，v(n)v(n) 和v*(n+l)是相互独立的随机过程，这种情况下噪声的循环自相关函数在循环频率上分布比较均匀，没有明显突起的峰；此外，在l大于零时Rv(l)为零，故噪声循环自相关函数的均值为零。噪声与信号的循环互相关函数为：

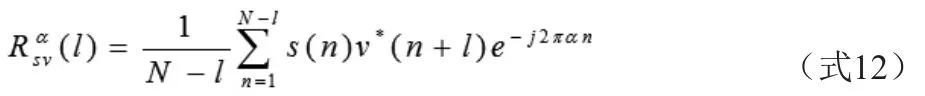
因噪声均值为零，故噪声与信号的循环互相关函数的均值为零。此外，信号与噪声是相互独立，且噪声一般是较均匀地分布于整个带宽，故信号与噪声的循环相关函数在信号载频附近会有较小的突起峰。

由以上分析可知，若噪声为白噪声，噪声循环自相关函数在循环频率上基本是平坦的，没有明显突起的峰，即噪声能量比较均匀地分布在整个带宽内。而在循环自相关输出中信号项的能量比较集中，有突起的峰，这种情况是有利于信号检测。

4.采用循环相关仿真试验

用循环自相关对步进线性调频信号进行验证和仿真。图2、3为分别为窗长80us和20us时，在不同信噪比下循环自相关的结果示意图。可以看出，循环自相关对于步进线性调频信号具有较好的能量积累的作用，并且受窗长的影响不大。在信噪比为-7dB的条件下，循环自相关的峰值与无噪声时的峰值相差不大。

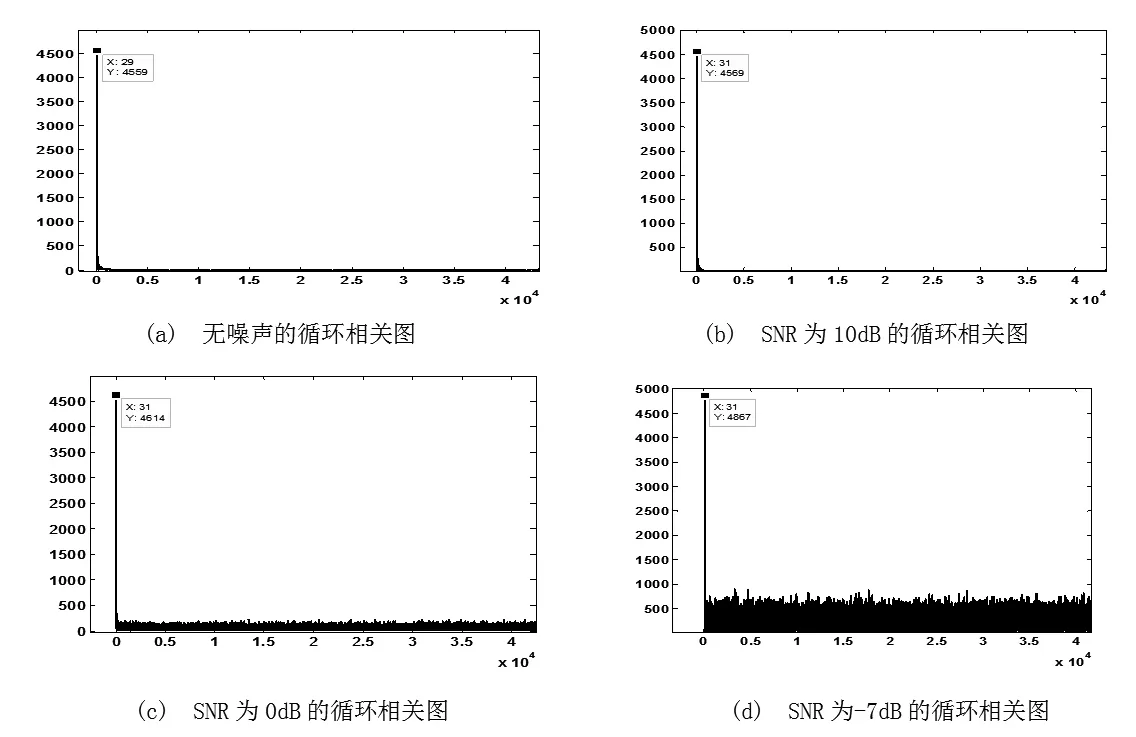
图2　线性调频步进信号在不同信噪比下的循环相关图(窗长为80 us)

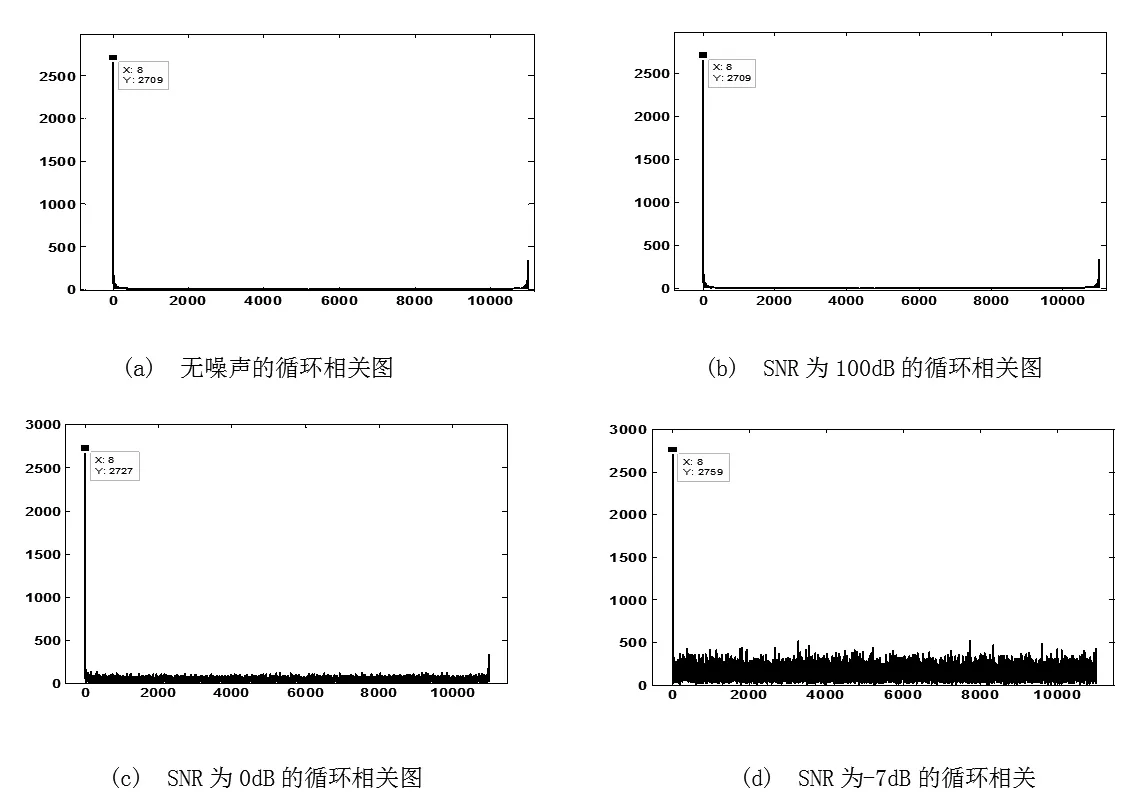
图3　线性调频步进信号在不同信噪比下的循环相关图(窗长为20 us)

5.结论

步进调频信号的每一个子脉冲都是线性调频信号，采用循环相关算法进行信号检测，不受信号采样窗长的制约，运算量适中，易于实现，信号检测灵敏度高，广泛应用于雷达信号的提取和检测。

[1]杨小牛,楼才义,徐建良.软件无线电技术与应用(第二版)[M].北京:北京理工大学出版社, 2014.

[2]杨万海.雷达系统建模与仿真[M].西安:西安电子科技大学出版社,2007.