基于变参数广义结构的距离扩展目标检测方法

王　智，简　涛，何　友

(海军航空大学信息融合研究所， 烟台 264001)

0　引　言

随着国家海洋战略逐步从近海走向远洋、从区域走向全球，迫切需要发展先进的海洋信息获取与处理技术。天基平台及其有效载荷是获取地球上各种信息的一种有效手段，在军事和民用中备受青睐[1]。《国家自然科学基金“十三五”发展规划》将海洋目标信息获取、融合与应用列为信息学部优先发展领域，并发布了“天空基海洋目标探测与识别基础研究”重大项目指南。高分辨率雷达作为天空基目标探测的重要手段之一，因其具有更大的带宽和更高的距离分辨率，在精确探测及成像、高精度跟踪、目标识别等方面具有明显的优势，获得了广泛的重视和应用[2]。

随着高分辨率雷达的广泛应用，距离扩展目标检测问题受到越来越多的关注[3]。针对高斯和复合高斯杂波背景下的距离扩展目标检测问题，学者们提出了许多最优或次优的自适应检测器。广义匹配滤波器(Generalized matched filter，GMF)[4]是高斯杂波背景下的最佳滤波器。在复合高斯背景下，文献[5]提出了归一化匹配滤波积累检测器(Normalized matched filter integrator，NMFI)。文献[6]针对天基雷达对海监视和跟踪，提出了一种基于波形自适应设计的目标检测算法，在低信杂比的杂波条件下可以有效检测目标。文献[7]则提出了两种距离扩展目标检测器，有效解决了非高斯杂波背景中检测具有稀疏散射点的距离扩展目标问题。

但是，实际杂波的非高斯特性往往在时间和空间上随环境的改变而渐进变化，这些特定杂波背景下的最优或次优检测器往往难以适应过渡杂波环境的快速变化，从而导致检测性能下降和恒虚警率(Constant false alarm rate，CFAR)特性恶化。针对上述问题，本文提出了融合检测器α-GMF，通过调整参数α∈[0,1]来适应杂波特性。当α= 0时，检测器演变为GMF；当α= 1时，检测器则演变为NMFI。这样，既考虑了极端的高斯和复合高斯杂波环境，也兼顾了介于高斯和复合高斯之间的过渡杂波环境。研究结果表明，在过渡杂波环境中，α-GMF的检测性能更好，对杂波非高斯程度时空渐变性具有较强的适应能力和泛化能力。

1　变参数广义结构检测器

1.1　问题描述

假设数据来源于N个线性阵元，需解决跨过H个距离单元zt(t= 1 ,…,H)检测一个目标存在与否。假设可能的目标完全包含在这些数据(主数据)中，并且忽略距离走动[8]的问题。假设可以利用不含目标回波的辅助数据集zt(t=H+1 ,…,H+R)，且每一个辅助数据都与主数据独立同分布。考虑杂波为主的干扰环境，忽略内部噪声的影响。所要解决的检测问题可以由以下二元假设检验来表达：

(1)

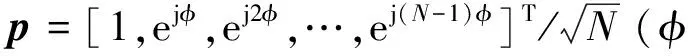
距离单元t的杂波向量ct采用球不变随机向量(Spherically invariant random vector，SIRV)[9]进行建模：

(2)

M=τ0Σ

(3)

1.2　检测器设计

当杂波为高斯杂波时，GMF能获得高斯杂波背景下的最优检测性能，其检测统计量为[4]：

(4)

当杂波非高斯性很强时，NMFI适合于复合高斯杂波背景下距离扩展目标检测，其检测统计量为[5]：

(5)

为使距离扩展目标检测器能适应于高斯和复合高斯杂波以及二者之间的过渡杂波环境，本文基于特定杂波环境下现有最优或次优检测统计量的共性特征，采用简洁的乘积形式融合构建距离扩展目标检测器，通过参数α实现距离扩展目标检测器设计与相应杂波环境的同步调整。在极端的高斯杂波背景下，取参数α=0，检测器演变为GMF；在极端的非高斯背景下，取α=1，此时检测器演变为NMFI。因此，本文将α-GMF的检验统计量表示为：

(6)

可以看出，本文所提出的距离扩展目标检测器结构涵盖高斯和非高斯等特定杂波背景下最优或次优距离扩展目标检测器GMF和NMFI，对实际杂波非高斯程度时空渐变性具有自适应能力，能有效提升高分辨率雷达在复杂杂波环境下的检测性能。

2　参数α的选取

2.1　参数α与检测门限的关系

本文首先考虑α的改变对恒虚警门限的影响。由于在点目标的情况下，恒虚警检测门限的计算涉及到一个二维无穷上限的积分[10]，并且距离扩展目标的情况会更加复杂，因此本文采用Monte Carlo仿真方法进行求解，参数α与检测门限的关系如图1所示。仿真中，虚警概率Pfa= 10-3，纹理分量的Gamma分布模型[11]为：

(7)

式中：Γ(·)是Gamma函数，v是形状参数，v越小，杂波就会出现越多的尖峰；b是均值，当b=1，距离单元中杂波的分布等效为K分布[10]。

图1给出了参数α∈[0,1]和形状参数v∈[0,+∞]时α-GMF的恒虚警检测门限。从图1可以看出：1)给定v时，当α由1递减至0，即α-GMF由NMFI变为GMF时，检测门限依次递増；2)给定α时，v越小，即杂波尖峰程度越高，检测门限也越高；3)当α趋于1，即α-GMF逐渐演变为NMFI时，检测门限对v的鲁棒性逐渐增强，当α= 1时检测门限与v无关。4)仅当N改变时，检测门限提高，而仅当H改变时，检测门限的范围扩大。

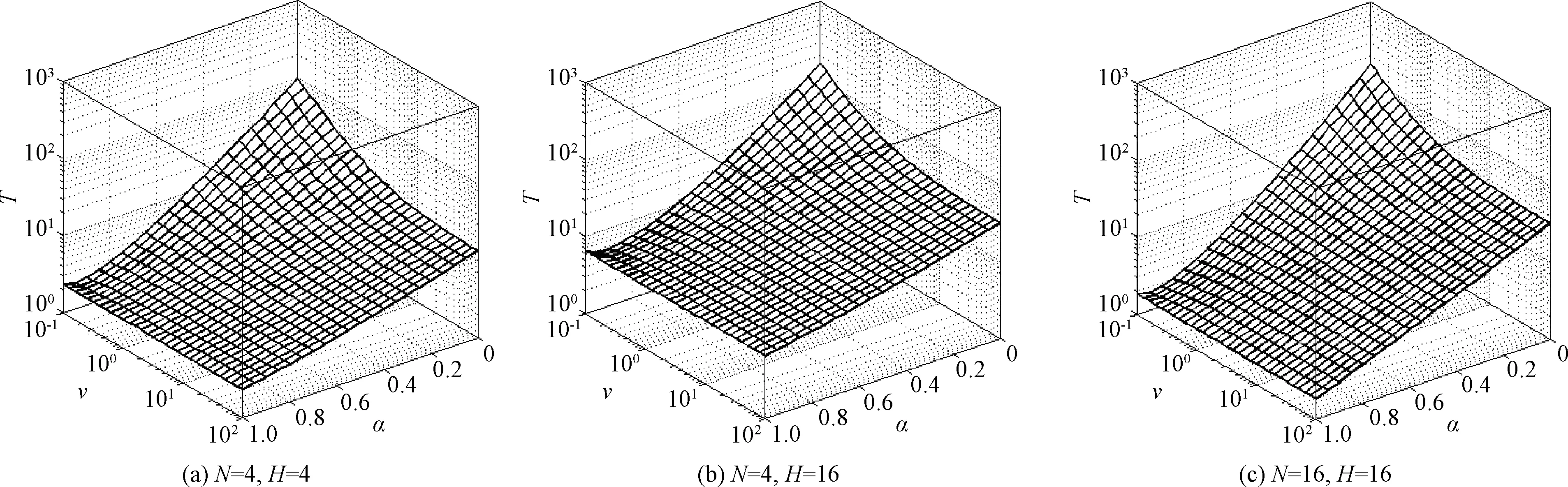
图1　检测门限与参数α和形状参数v的变化关系Fig.1　The relationship between the threshold with the parameter α and the shape parameter v

由于检测门限T与阵元数N,检测距离单元数H,形状参数v和控制参数α有关，因此在给定虚警概率Pfa的条件下，参数α可以用关于N,H和v的函数表示。

2.2　参数α的经验公式

α-GMF通过调整参数α来适应不同杂波环境，其检测性能与α的取值紧密相关。选择参数α实质上是评定检测器的检测性能，即选择使检测器检测效果达到最佳时的参数α。当给定虚警概率Pfa时，主要通过信杂比SCR随检测概率Pd变化的曲线，即ROC曲线(Receiver operating characteristic curve)[12]来评定检测器的检测性能，ROC曲线下的面积越大意味着检测器性能越好。

当检测概率低于0.5时，对于大多数雷达来说不足以形成一个稳定的目标轨迹，故选取ROC曲线下且Pd≥ 0.5的区域来评定α-GMF的检测性能[13]。设Pd(v,α,ρ)为给定虚警概率下α-GMF的检测概率，则积分区域定义为：

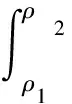
(8)

(9)

式中:ρ表示杂波白化后的SCR。

由于α-GMF在K分布杂波背景下的CFAR门限T和检测概率Pd不能通过简单的表达式表示，参数α和v之间的关系式(8)也得不到具体的数值表达式。在此，本文通过数值计算寻求最佳参数α的经验公式，其中ρ1= -10 dB，ρ2= 20 dB，仿真结果如图2所示。

从图2可以看出：1)当形状参数v从0变化至无穷大时，参数α逐渐由1减小至0，即v与α成反比关系，这符合NMFI估计适合长尾拖的非高斯杂波而GMF估计对高斯杂波是最优的。2)在H相同的情况下，N越大，随着v的增加，参数α减小越慢。3)在N相同的情况下，H越大，α在非高斯性较强的条件下取值越大，随后α迅速衰减；当杂波趋于高斯杂波时，α衰减趋势趋于一致。

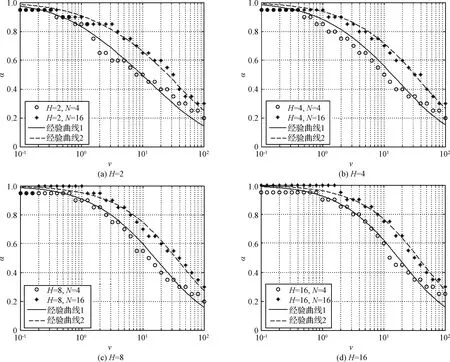
图2　检测器参数α的经验曲线Fig.2　The empirical curves of the detector parameter α

采用归一化均方误差 (Normalized mean square error, NMSE) 作为拟合α经验公式的标准， 其表达式为：

(10)

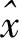
(11)

图2中的曲线是参数α的经验曲线，其ε的值如表1所示。可以看出，经验公式(11)符合数值结果。

表1　不同条件下ε的值Table 1　Values of ε under different conditions

3　性能分析

本节在K分布杂波背景下，对α-GMF的检测性能进行仿真分析，并与GMF和NMFI进行对比。仿真中，为控制计算量，设定虚警概率Pfa= 10-3；检测阈值T和检测概率Pd均采用Monte Carlo方法计算，为保证计算精度，仿真次数为105次。纹理分量采用Gamma分布模型，数据是由计算机模拟产生的；杂波归一化协方差矩阵Σ采用指数相关结构进行建模[14]：

(12)

式中：γ表示杂波的一阶相关系数。将仿真目标信号添加到杂波数据中，验证所提检测器的有效性。

令h0表示目标等效散射点个数，并且一个距离单元最多只有一个散射点，本文考虑5种典型的散射点能量分布模型[15]，如表2所示。

模型1表示目标能量在h0个距离单元内均匀分布；模型2～4表示有一个距离单元的目标能量最强，剩余h0- 1个距离单元内目标能量均匀分布；模型5表示能量全部集中在一个距离单元中，相当于点目标的情况。图3～图8给出了不同条件下α-GMF的检测性能曲线。

表2　几种典型散射点能量分布模型Table 2　Several typical scattering energy distribution models

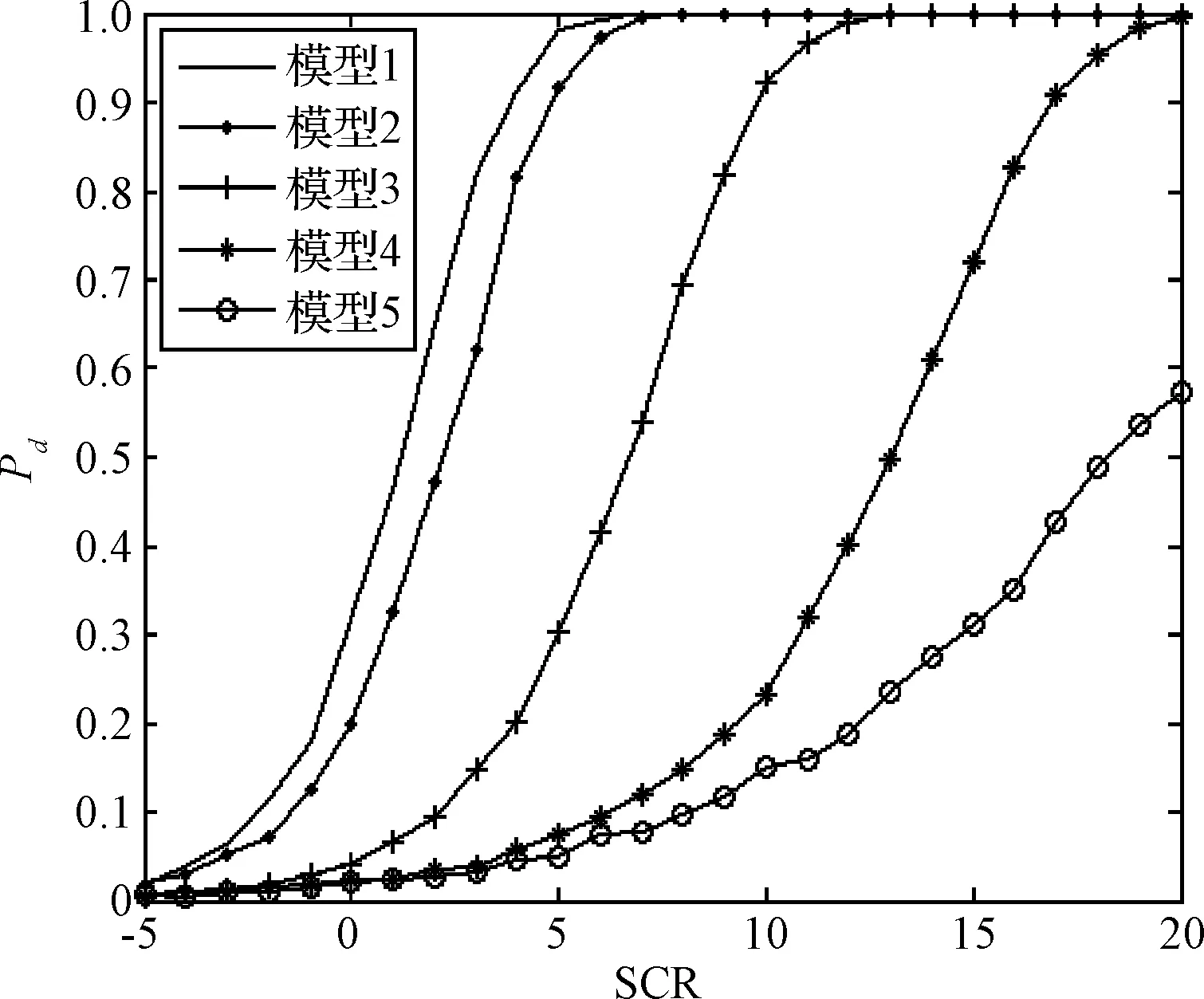
图3　模型1～5, τ0=1, γ=0, v=2, N = 4, h0 = H = 8时α-GMF 检测性能曲线Fig.3　ROC curves of α-GMF when model 1～5, τ0=1, γ = 0, v=2, N=4, h0=H=8

在τ0= 1，γ= 0，v=2，N=4，h0=H=8时，图3分析了不同散射点能量分布对检测器的影响。从图3可以看出，目标等效散射点能量均匀分布(模型1)时，α-GMF的检测性能最好；目标能量越集中，α-GMF的检测性能下降越快，损失越大；在极端的点目标环境下(模型5)，只有当SCR > 19时α-GMF的检测概率才大于0.5，说明此时检测器存在极大的检测损失。可能的原因是，在点目标环境下，检测统计量对纯杂波的距离单元进行了积累，存在坍塌损失；且目标能量越集中，越接近于点目标，坍塌损失越大[16]。为了便于分析，下文均采用模型1进行分析。

图4给出了阵元数N= 2, 4, 8,16时α-GMF的检测性能曲线，由图4可知，检测性能随着N的增加而提高。图5给出了检测距离单元H不同时的检测性能曲线，可以看出，α-GMF的检测性能同样随H的增加逐步提高。图6分析了杂波功率水平τ0和协方差矩阵一阶相关系数γ对检测器性能的影响，可以看出，α-GMF的检测性能不受参数τ0和γ的影响。

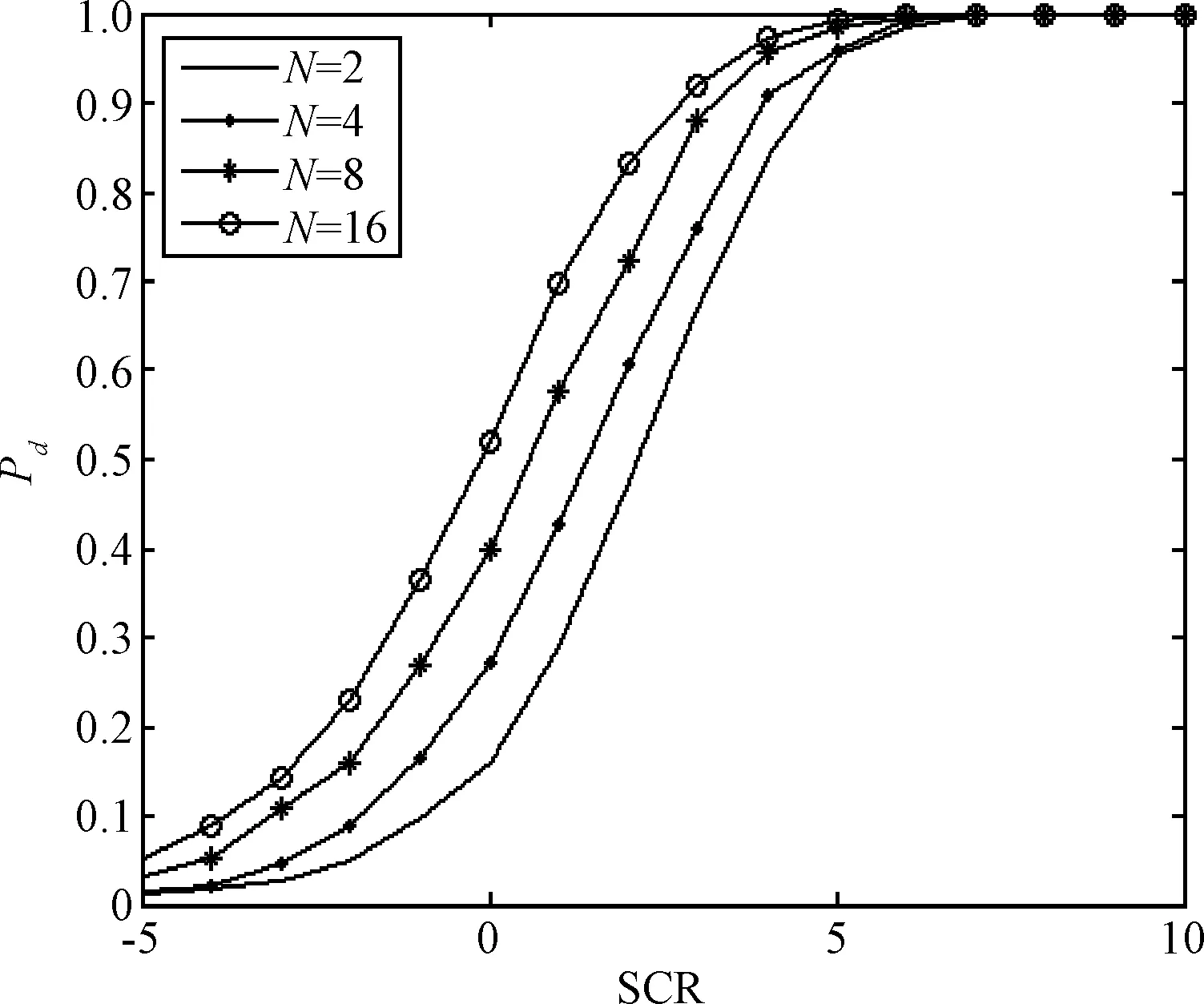
图4　τ0=1, γ = 0, v=2, N=2,4,8,16, h0=H=8时α-GMF检测性能曲线Fig.4　ROC curves of α-GMF when τ0=1,γ = 0, v=2, N=2,4,8,16, h0=H=8

图5　τ0=1, γ = 0, v=2, N=4, h0=H=2,4,8,16时α-GMF检测性能曲线Fig.5　ROC curves of α-GMF when τ0=1, γ = 0, v=2, N = 4, h0=H=2,4,8,16

图7　τ0=1, γ = 0, v =0.5,2,8和100, N=4, h0=H=8时α-GMF检测性能曲线Fig.7　ROC curves of α-GMF when τ0=1, γ = 0, v=0.5,2,8,100, N = 4, h0=H=8

图8　τ0=1, γ = 0, v=2, N=4, h0=2,4,6,8, H=8时α-GMF检测性能曲线Fig.8　ROC curves of α-GMF when τ0=1, γ = 0, v =2, N = 4, h0 = 2,4,6,8, H=8

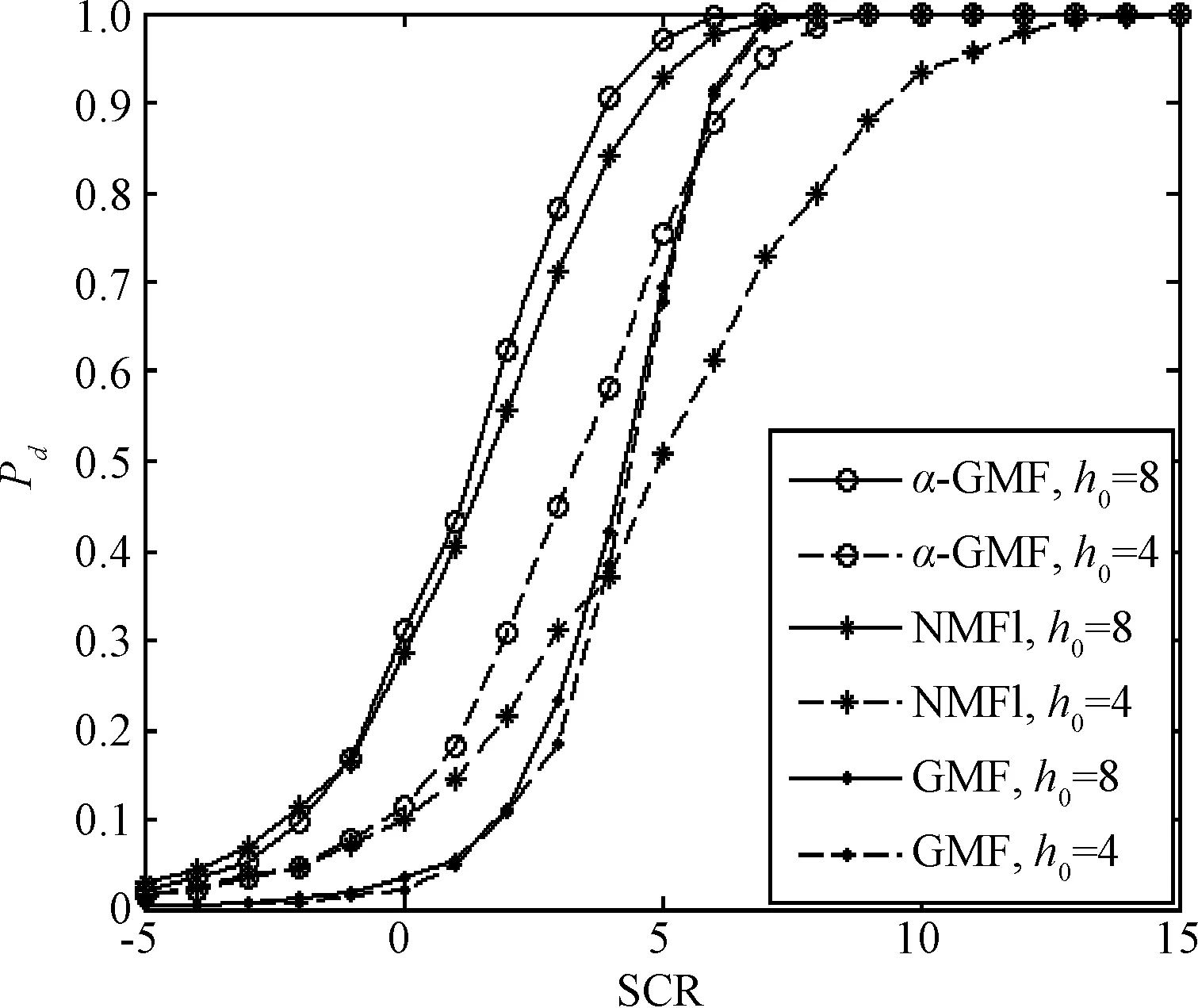
图9　τ0=1, γ = 0, v=2, N=4, h0 =4,8, H=8时α-GMF、GMF和NMFI检测性能曲线Fig.9　ROC curves of α-GMF, GMF and NMFI when τ0=1, γ = 0, v=2, N= 4, h0= 4, 8, H=8

针对v=0.5, 2, 8,100的情况，图7分析了杂波的尖峰程度v对α-GMF检测性能的影响。由图7可知，α-GMF的检测性能先随v的减小而下降，但当杂波趋于高斯杂波(v=100)时，其检测性能又略有提升。另外，图8评估了不同的散射点密度(h0= 2, 4, 6, 8)对α-GMF检测性能的影响。从图8可以看出，在H相同的条件下，h0越小，散射点越稀疏，坍塌损失越大，当h0取1时就相当于点目标的情况，这与图3中的结果类似。

图9在τ0=1，γ= 0，v=2，N=4，h0=4，8，H=8的条件下，对α-GMF,GMF和NMFI的检测性能进行对比分析。从图9可以看出，在散射点密集(h0=H=8)的条件下，对于给定Pd≥ 0.5，α-GMF所需的SCR仅比NMFI少0.5 dB左右，而比GMF少3～4 dB，说明α-GMF的检测性能略优于NMFI，但明显优于GMF。在散射点稀疏(h0=4)的条件下，α-GMF和NMFI的检测性能有所降低，而GMF的检测性能基本不变；当0.5 ≤Pd< 0.8时，α-GMF检测性能优于GMF，而GMF在Pd> 0.8时检测性能更好，并且α-GMF和GMF在给定Pd≥ 0.5时检测性能明显优于NMFI。这是因为NMFI是积累检测器，其检测性能与积累的距离单元数密切相关，目标散射点越稀疏，NMFI受到损失越大。

综合来看，在介于高斯和复合高斯杂波之间的过渡环境中，α-GMF比GMF和NMFI具备更加优异的目标检测性能，体现了α-GMF对实际杂波非高斯程度时空渐变性的自适应性能。

4　结　论

针对特定杂波背景下的最优或次优检测器结构难以适应过渡杂波环境的问题，本文提出了基于变参数广义结构的距离扩展目标检测器α-GMF，并通过调整参数α使检测器适应杂波特性。研究结果表明：1)α-GMF在目标能量均匀分布时检测性能最好, 并且阵元数和检测距离单元数越多、散射点越密集检测性能越好，但随着散射点能量的集中，检测器性能逐渐下降。2)在介于高斯和复合高斯杂波之间的过渡环境中，α-GMF比GMF和NMFI具备更加优异的目标检测性能，体现了α-GMF对实际杂波非高斯程度时空渐变性的自适应性能，具有较强的泛化能力。

[1]徐一帆, 谭跃进, 贺仁杰, 等. 天基海洋目标监视的系统分析及相关研究综述[J]. 宇航学报, 2010, 31(3): 628-640. [ Xu Yi-fan, Tan Yue-jin, He Ren-jie, et al. System analysis and research overview of space-based maritime surveillance [J]. Journal of Astronautics, 2010, 31(3):628-640.]

[2]郭启俊. 雷达信号恒虚警率检测及空间信号源数估计[D]. 西安: 西安电子科技大学, 2007. [Guo Qi-jun. CFAR detection of radar signal and estimation of spatial signal sources [D]. Xi’an: Xidian University, 2007.]

[3]简涛, 何友, 苏峰, 等. 高距离分辨率雷达目标检测研究现状与进展[J]. 宇航学报, 2010, 31(12): 2623-2628. [Jian Tao, He You, Su Feng, et al. Overview of high range resolution radar target detection [J]. Journal of Astronautics, 2010, 31(12): 2623-2628.]

[4]Conte E, De Maio A, Ricci G. GLRT-based adaptive detection algorithms for range-spread targets [J]. IEEE Transactions on Signal Processing, 2001, 49(7): 1336-1348.

[5]顾新锋, 简涛, 何友, 等. 非高斯杂波背景中距离扩展目标的盲积累检测器[J]. 航空学报, 2012, 33(12): 2261-2267. [Gu Xin-feng, Jian Tao, He You, et al. Blind integrator for range-spread target in non-Gaussian clutter [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2261-2267.]

[6]王海涛, 叶琦, 刘爱芳, 等. 基于自适应波形设计的天基雷达目标检测方法[J]. 宇航学报, 2013, 34(8): 1130-1136. [Wang Hai-tao, Ye Qi, Liu Ai-fang, et al. Target detection based on adaptive waveform design for space based radar [J]. Journal of Astronautics, 2013, 34(8):1130-1136.]

[7]顾新锋, 简涛, 何友, 等. 非高斯杂波背景中的两个距离扩展目标检测器[J]. 宇航学报, 2012, 33(5): 648-654. [Gu Xin-feng, Jian Tao, He You, et al. Two detectors of range-spread target in non-Gaussian clutter [J]. 2012, 33(5): 648-654.]

[8]Gerlach K. Spatially distributed target detection in non-Gaussian clutter [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 926-934.

[9]De Maio A, Conte E. Uniformly most powerful invariant detection in spherically invariant random vector distributed clutter [J]. IET Radar, Sonar and Navigation, 2010, 4(4): 560-563.

[10]Shui P L, Liu M, Xu S W. Shape-parameter-dependent coherent radar target detection in K-distributed clutter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(1): 451-465.

[11]顾新锋, 简涛, 何友, 等. 协方差矩阵结构的广义杂波分组估计方法[J]. 宇航学报, 2012, 33(12): 1794-1800. [Gu Xin-feng, Jian Tao, He You, et al. Generalized clutter-clustered estimation of covariance matrix structure [J]. Journal of Astronautics, 2012, 33(12): 1794-1800.]

[12]Sofotasios P C, Fikadu M K, Ho-Van K, et al. The area under a receiver operating characteristic curve over enriched multipath fading conditions[C]. IEEE Global Communications Conference,Austin, USA, December 7-11, 2014.

[13]刘明. 海杂波中微弱运动目标自适应检测方法研究[D]. 西安: 西安电子科技大学, 2016. [Liu Ming. Research on adaptive detection methods of weak moving targets in sea clutter [D]. Xi’an: Xidian University, 2016.]

[14]Conte E, De Maio A, Ricci G. Covariance matrix estimation for adaptive CFAR detection in compound-Gaussian clutter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 415-426.

[15]Jian T, He Y, Su F, et al. Adaptive range-spread target detection based on modified generalized likelihood ratio test in non-Gaussian clutter [J]. IET Radar, Sonar and Navigation, 2011, 5(9): 970-977.

[16]简涛, 黄晓冬, 王捷, 等. 基于修正最大似然估计的距离扩展目标检测器[J]. 武汉大学学报(信息科学版), 2016, 41(6): 791-796. [Jian Tao, Huang Xiao-dong, Wang Jie, et al. Range-spread target detector based on modified maximum likelihood estimation[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 791-796.]