JULIA SETS AS JORDAN CURVES

ZHUANG Wei

(Department of Mathematics and Physics,Beijing Institute of Petrochemical Technology,Beijing 102617,China)

1　Introduction and Main Results

Let f(z)be a rational map of degree d=degf≥2 on the complex sphere.The Julia set J(f)of a rational function f is defined to be the closure of all repelling periodic points of f,and its complement set is called Fatou set F(f).It is known that J(f)is a perfect set(so J(f)is uncountable,and no point of J(f)is isolated),and also that if J(f)is disconnected,then it has infinitely many components.

for every x∈X and fnis topologically conjugate to a subshift of finite type.If only condition|(fn)′(x)|＞ 1 is satisfied,we call the map f|Xexpanding.

We call a rational function f:J(f)→ J(f)hyperbolic if there exists n ≥ 1 such that

Denote CV(f)the critical values of a rational function f.Let

It follows from[1,Theorem 2.2]that a rational function f:J(f)→ J(f)is hyperbolic if and only if

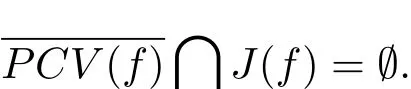
Denote by J(f)the Julia set of a rational function.A rational map f is expansive if the Julia set J(f)contains no critical points of f.It follows from[1]that each hyperbolic rational function is expansive and that a rational function is expansive but not hyperbolic if and only if the Julia set contains no critical points of f but intersect the ω-limit set of critical points.

We call expansive but not hyperbolic rational functions parabolic.It follows from[1]that a rational function f:J(f)→ J(f)is expansive but not hyperbolic if and only if the Julia set J(f)contains no critical points of f but contains at least one parabolic point.

We recall that if T:X→X is a continuous map of a topological space X,then for every point x ∈ X,the ω-limit set of x denoted by ω(x)is defined to be the set of all limit points of the sequence{Tn(x)}n≥0.We call a point x recurrent if x ∈ ω(x);otherwise x is called non-recurrent.

The class of NCP maps obviously contains all expanding and parabolic maps.It also comprises the important class of so called subexpanding maps which are defined by the requirement that f|ω(Crit(f))∩J(f)is expanding and the class of geometrically finite maps defined by the property that the forward trajectory of each critical point contained in the Julia set is finite and disjoint from ω-limit set.

Let f(z)be a map of degree≥2.A component D of the Fatou set F(f)is said to be completely invariant,if

In this paper,we establish the following main theorem.

Main TheoremLet f(z)be an NCP map of degree≥2,and suppose that F(f)is the union of exactly two completely invariant components.Then J(f)is their common boundary and is a Jordan curve.

2　Preliminaries and the Construction of a Net

Let f be an NCP map.Denote by Λ(f)the set of all parabolic periodic points of f(these points belong to the Julia set and have an essential influence on its fractal structure),and Crit(f)of all critical points of f.We put

Set

Definition 2.1We define the conical set Jc(f)of f as follow.First,say x belongs to Jc(f,r)if for any∈＞0,there is a neighborhood U of x and n＞0 such that diam(U)＜ε and fn:U→B(fn(x),r)is a homeomorphism.Then setWe have x∈Jc(f)if and only if arbitrary small neighborhood of x can be blow up univalently by the dynamics to balls of definite size centered at fn(x).

Lemma 2.1(see[2])If f:J(f)→J(f)is an NCP map,then

Note that Curtis T.McMullen used the term radial Julia set Jrad(f)instead of conical set Jc(f)in analogy with Kleinian groups,see ref.[3].By paper[3],we have the set Sing(f)is countable.

Let 0＜λ＜1.Then there exist an integer m≥1,C＞0,an open topological disk U containing no critical values of f up to order m and analytic inverse branchesof fmn(i=1,···,kn≤ dnm,n ≥ 0),satisfying

(3)for each fixed n ≥ 1,for all i=1,···,knthe setsare pairwise disjoint and

Now we state as a lemma the following consequence of(1)–(3).

Lemma 2.2For each n,letand letThen N is a net of Jc(f),i.e.,any two sets in N are either disjoint or one is a subset of the other.

3　Conformal Iterated Function System

In paper[4],Urbanski and Zdunik provided the framework to study infinite conformal iterated function systems.Now we recall this notion and some of its basic properties.Let I be a countable index set with at least two elements and let S={φi:X → X:i∈ I}be a collection of injective contractions from a compact metric space X(equipped with a metric ρ)into X for which there exists 0 ＜ s ＜ 1 such that ρ(φi(x),φi(y)) ≤ sρ(x,y)for every i∈I and for every pair of points x,y∈X.Thus system S is uniformly contractive.Any such collection S of contractions is called an iterated function system.We are particularly interested in the properties of the limit set defined by such a system.We can define this set as the image of the coding space under a coding map as follows.Letthe space of finite words,and for τ∈ I∗,n ≥ 1,let φτ= φτ1◦ φτ2◦ ···◦ φτn.Letbe the set of all infinite sequences of elements of I.If τ∈ I∗∪I∞and n ≥ 1 does not exceed the length of τ,we denote by τ|nthe word τ1τ2···τn.Since given τ∈ I∞,the diameters of the compact sets φτ|n(X),n ≥ 1,converge to zero and since they form a descending family,the set

is a singleton therefor,denoting its only element by π(τ),defines the coding map

有 8 篇研究[2，4-8，11]报道了Ⅲ度及以上腹泻，合计样本量504例：替吉奥组252例，卡培他滨组252例。各研究间具有同质性（P=0.92，I2=0%），采用固定效应模型。结果显示，替吉奥组Ⅲ度及以上腹泻少于卡培他滨组，具有统计学意义[RR=0.42，95%CI：（0.18，0.99），P=0.05]，见图 3。

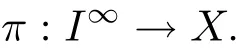
The main object in the theory of iterated function systems is the limit set defined as follows.

Observe that J satisfied the natural invariance equality

Notice(1)If I is finite,then J is compact and this property fails for infinite systems by paper[4].

(2)In Lemma 3.3,we shall build recursively our iterated function systemand n(=I)is finite.

Let X(∞)be the set of limit points of all sequences xi∈ φi(X),i∈ I′,where I′ranges over all infinite subsets of I,see ref.[4].

Lemma 3.1(see[4])If

An iterated function system S={φi:X → X:i∈ I}is said to satisfy the open set condition if there exists a nonempty open set U⊂X(in the topology of X)such that φi(U)⊂ U for every i∈ I and φi(U)∩φj(U)= ∅ for every pair i,j∈ I,i/=j(we do not exclude clφi(U)∩ clφj(U)/= ∅).

An iterated function system S={φi:X →X:i∈I}is said to be conformal if X ⊂Rdfor some d≥1 and the following conditions are satisfied.

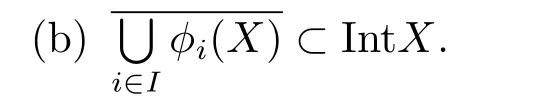
(c)There exists an open connected set V such that X⊂V⊂Rdsuch that all maps φi,i ∈ I,extend to C1conformal diffeomorphisms of V into V(note that for d=1 this just means that all the maps φi,i ∈ I,are monotone diffeomorphism,for d=2 the words conformal mean holomorphic and antiholomorphic,and for d=3,the maps φi,i ∈ I are Möbius transformations).

(d)(Cone condition)There exist α,l＞ 0 such that for every x ∈ ∂X and there exists an open cone Con(x,u,α)⊂ Int(V)with vertex x,the symmetry axis determined by vector u of length l and a central angle of Lebesgue measure α,here Con(x,u,α)={y:0 ＜ (y−x,u)≤cosα||y−x||≤ l}.

(e)Bounded distortion property(BDP).There exists K≥1 such that

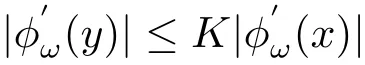
for every ω ∈ I∗and every pair of points x,y ∈ V,wheremeans the norm of the derivative,see ref.[9,10].

Definition 3.1A bounded subset X of a Euclidean space(or Reimann sphere)is said to be porous if there exists a positive constant c＞0 such that each open ball B centered at a point of X and of an arbitrary radius 0＜r≤1 contains an open ball of radius cr disjoint from X.If only balls B centered at a fi xed point x∈X are discussed above,X is called porous at x,see ref.[5].

Lemma 3.2(see[5])The Julia set of each NCP map,if diあerent fromis porous.

Lemma 3.3If f is an NCP map,then Jc(f)admits a conformal iterated function system satisfying conditions(a)–(e).

ProofLet f be an NCP map.By Lemma 2.2,Jc(f)admits a net such that Bi∩Bj= ∅,i/=j.Moreover,we may require the existence of an integer q≥ 1 and σ ＞ 0 such that the following holds:

If x∈Jc(f),say x∈Bi,and fqn(x)∈Bt,then there exists a unique holomorphic inverse branch:sending fqn(x)to x.Moreoverand taking q suきciently large,we have

for suきciently small σ,then

Let n ＞ 1 be fi nite.For every t=1,2,···,n,we now build recursively our iterated function system Stas a disjoint union of the familiesj≥1,as follows.consists of all the maps,where x,fq(x)∈ Jc(f)∩ Bt.consists of all the mapswhere x,f2q(x)∈Jc(f)∩Btand fq(x)/∈Bt.Suppose that the familieshave been already constructed.Thenis composed of all the mapssuch that y,fqn(y)∈Jc(f)∩Btand fqj(y)∈/Btfor every 1≤j≤n−1.

Let V⊃Jc(f)be an open set constructed by the net such that it disjoints from the parabolic and critical points and their inverse orbits of f.For any x∈V and fi nite n＜∞,we have

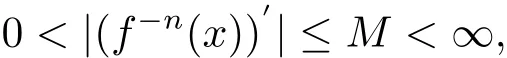
then

where x,y∈V and 1≤K＜∞is a constant.So condition(e)bounded distortion property(BDP)holds.It is evident that fnis holomorphic and antiholomorphic of V into V for all n≥1,then condition(c)holds.Since J(f)is porous,and condition(d)is satis fi ed.Condition(b)follows immediately from(3.1).In order to prove condition(a),take two distinct mapsandbelong to St.Without loss of generality we may assume that m≤n.Suppose on the contrary that

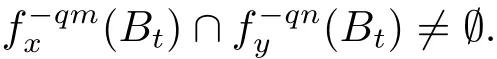
Then

4　Proof of Main Result

Given x∈C,θ,r＞ 0,we put

where η is a representative of θ.We recall that a set Y has a tangent in the direction θ at a point x∈Y if for every r＞0,

where H1denotes the 1-dimensional Hausdorff measure(see refs.[6,7]).Following[6],we say that a set Y has a strong tangent in the direction θ at a point x provided for each 0＜ β ≤ 1,there is a some r＞ 0 such that Y ∩B(x,r)⊂ Con(x,θ,β).

Lemma 4.1(see[7])If Y is locally arcwise connected at a point x and Y has a tangent θ at x,then Y has strong tangent θ at x.

We call a point τ∈ I∞transitive if ω(τ)=I∞,where ω(τ)is the ω-limit set of τ under the shift transformation σ :I∞→ I∞.We denote the set of these points byand putWe call the Γtthe set of transitive points of ΓStand notice that for everythe setis dense in

Lemma 4.2(see[7])has a strong tangent at a point x= π(τ),τ∈ I∞,then ΓSt has a strong tangent at every point

Remark 4.1If f is an NCP map,by Lemma 3.3,Jc(f)admits a conformal iterated function system St.It is obvious that the Julia set J(f)coincides with the limit setby Lemma 3.1.By Lemma 3.1,3.3 and 4.2 we have

Lemma 4.3If f is an NCP map,then J(f)has a strong tangent at every point of J(f).

Proof of Main TheoremLet f be an NCP map and denoted by F∞the unbounded component of the Fatou set F(f).As F∞is completely invariant,applying Riemann-Hurwitz formula(see§5.4 in[8])to f:F∞→ F∞,we find that F∞has exactly d−1 critical points of f,and all of these lie at∞.Now take any disk D centered at∞,which is such that

For each n,let Dn=f−n(D):then Dnis open and connected,

and as

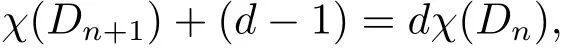
where χ(Dn+1)and χ(Dn)denote the Euler characteristics of domains Dn+1and Dnas above,we see that each Dnis simply connected.Let γnbe the boundary of Dn;then γnis a Jordan curve and fnis a dn-fold map of γnonto γ0.SetRoughly speaking,we shall show that γnconverges to

If ξ∈ Γ then there are points ξnon γnwhich converge to ξ,so,in particular,ξ is in the closure of F∞.However,ξ cannot lie in F∞else it has a compact neighbourhood K lying in some Dn(for the Djare an open cover of K),and hence not meeting γn,γn+1,···for sufficiently large n.We deduce that Γ ⊂ J(f).

J(f)is porous,then Jc(f)admits a conformal iterated function system s}for finite s satisfying conditions(a)–(e)by Lemma 3.3.

To prove that J(f)⊂Γ,let w∈J(f)be a repelling fixed point(or an image of a repelling fixed point)and l be the straight line determined by the strongly tangent direction of J(f)at w as in Lemma 4.3.Then w is an attracting fixed point of f−1.Moreover,

is a conformal map,where U(w)is a disk centered at w.Now suppose that J(f)is not contained in Γ.Consider x ∈ J(f)Γ such that x ∈ U(w),thenand for every n ≥ 0,we have f−n(x)∈ J(f).Since the map f−1:U(w)→ U(w)is conformal,we get

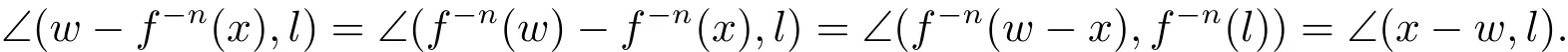
It follows that w and f−n(x)(n ≥ 0)are contained in the same lineand this implies thatis the strongly tangent straight line of J(f)at w.Therefore,we conclude that l is not a strongly tangent straight line of J(f)at w.This contradiction proves that J(f)⊂ Γ.

RemarkIf Main Theorem only with the hypothesis:the Fatou set F(f)has a completely invariant component,J(f)need not be a Jordan curve;for example,the map z→ z2−1 is expanding on its Julia set(certainly NCP map),see Theorem 9.7.5 and Figure 1.5.1 in[8].

[1]Urba´nski M.Measures and dimensions in conformal dynamics[J].Bull.Amer.Math.Soc,2003,40:281–321.

[2]Urba´nski M.Rational functions with no recurrent critical points[J].Ergod.Th.Dynam.Sys.,1994,14:391–414.

[3]Curtis T McMullen.Huasdorff dimension and conformal dynamics II:Geometrically finite rational maps[J].Comment Math.Helv.,2000,75:535–593.

[4]Urba´nski M,Zdunik A.Hausdorff dimension of harmonic maesure for self-conformal set[J].Adv.Math.,2002,171:1–58.

[5]Przytycki F,Urba´nski M.Porosity of Julia sets of non-recurrent and parabolic Collet-Eckmann rational functions[J].Ann.Acad.Fenn.,2001,26:125–154.

[6]Mauldin R D,Urba´nski M.Jordan curvers as repellors[J].Pac.J.Math.,1994,166:85–97.

[7]Mauldin R D,Mayer V,Urba´nski M.Rigidity of connected limit sets of conformal IFS[J].Michigan Math.J.,2001,49:451–458.

[8]Beardon A F.Iteration of rational functions[M].No.132 in GTM,New York:Springer-Verlag,1991.

[9]Zhuang Wei.On the continuity of Julia sets and the Hausdorff dimension of Yang-Lee zeros[J].J.Math.,2013,33(4):571–583.

[10]Zhuang Wei.The property of the Julia set of rational functions with conformal iterated function system[J].J.Math.,2007,27(2):177–180.