磁制动作用下太阳在主序阶段质量流失对自转角速度减速的影响

李林森

(东北师范大学物理学院长春130024)

1 引言

研究太阳的演化是太阳物理学的一项主要课题,因为太阳过去和未来的演变关系到我们地球的未来.太阳的演变包括其自转的演化,故此,研究太阳自转演变也是一项很有意义的重要课题.

天文工作者对于太阳自转的研究已有100多年的历史,文献[1]1976年从理论方面研究了太阳自转,文献[2]和文献[3]分别在1984年和1985年从观测方面研究了太阳的自转.他们的研究已在文献[4]2013年发表的题为“太阳较差自转130年(1855–1985)的观测和理论研究史的回顾”一文做了介绍.研究太阳自转主要研究太阳的自转角动量和自转角速度的演变.

太阳从星际气体云诞生后所有物理参量都已确定,包括自转角动量和自转角速度.早期太阳的角动量要比目前的角动量大两个数量级,磁场也较强,磁活动激烈,发射粒子造成质量损失[5].角动量之所以减少的原因除太阳风损失质量外,主要还有磁场对自转起减速的磁制动作用.在太阳一生演化过程中,这两种作用始终扮演重要角色.根据力矩对角动量制动的理论分析,对于太阳角动量损失而言,磁转矩所起的贡献比太阳风直接带走的角动量更大[6].可见磁制动作用对太阳自转减速起主导作用,但太阳风的作用也不能忽视.据估计,角动量减少的特征时间(角动量与其角动量损失率之比)与太阳本身的年龄接近,从而意味着太阳风大大改变了太阳的总角动量[6−7].然而,根据文献[8]的观测,太阳磁场与t−1/2成正相关,随时间增加而减弱,这说明目前太阳的磁场比过去减弱了很多,因而,磁制动作用也减少了不少.然而,根据文献[1]所言,太阳发射Ca II谱线表示太阳仍有较强磁场,再加上太阳黑子的磁场最强达4000 Gs,仍有磁制动作用,但这并不代表太阳的总磁场.目前太阳的总磁场并不强.太阳磁场由发电机产生,文献[9]1957年研究了太阳磁流体发电机理论;文献[10]2007年研究了轴对称和非对称的太阳磁场的发电机模型.

根据以上所述,研究太阳角动量的制动作用仍需考虑磁制动和太阳风的两种作用.文献[11]研究了太阳在主序阶段质量流失对自转减速的影响.文献[12]1990年研究了太阳风对太阳自转减速的影响.文献[13]2015年研究了太阳在主序前半程因质量损失对自转减速的影响.文献[14]2016年研究了自转星因质量损失造成的自转角速度减速.然而,这些作者只考虑太阳风的减速的制动作用,没有考虑磁制动作用.文献[15]1948年研究了太阳内部磁力线对角动量的制动作用.文献[8]1972年从观测太阳发射的CaII研究了磁制动作用和太阳自转的关系.文献[16]2009年给出了磁性黑子对星风和角动量的影响.文献[17]2014年从黑子发电机的定标研究了类似太阳的自转磁体星,讨论了黑子发电机与磁制动和自转的关系,这似乎说明了强磁场的黑子是发电机之源.文献[18–19]2013年研究了类似太阳的恒星的角动量模型并给出具有发电机的新的制动定律,并于2015年给出前文角动量模型的改进,包括新的磁风制动、发电机和质量损失.文献[20]2016年研究了类似太阳恒星的自转模型,自转的制动定律包括外部星风转矩和内部角动量运输过程.文献[21]2016年研究了老年恒星快速自转和弱磁制动的关系.所有这些研究说明了磁制动作用对太阳自转减速的影响.作者在前文献[12–14]只考虑了太阳风的制动作用,没有考虑磁制动对自转减速的作用.特别文献[13]的研究是太阳在主序前半程半径视为常数的情况下作出的,并没有考虑磁制动作用下给出的理论结果.至于太阳在主序后半程因半径改变较大没有研究.本文不仅考虑主序前半程也考虑后半程的磁制动效应,研究了太阳在整个主序阶段(100亿年)内质量流失对自转角速度改变的影响.文献[1]虽然给出了在磁制动作用下太阳角速度变化的理论,但没有给出在主序前半程和后半程自转角速度改变的数值.本文除理论上做了详细推算外,在数值计算方面也做了一些工作.

2 太阳磁制动和质量流失对自转角速度减慢的影响

文献[13]在不考虑磁制动作用时,角动量守恒可写为

其中Ω为角速度.当考虑磁制动作用时,太阳半径R必须用Alfven半径rA表示,角动量损失率应该写成[1,6]

Ωs是太阳表面的角速度.

太阳质量损失率由下式给出[1]:

式中,vA和ρA分别表示太阳表面发射出的粒子速度和密度.将(3)式代入(2)式后有

根据Alfven-Mach数的定义,应该有

BA是用Alfven表示的表面磁场,因此,

将(5)式代入(4)式有

根据文献[1]和[6]太阳磁场起源于太阳发电机的理论,磁场依赖太阳自转角速度.文献[8]从观测方面、文献[22]从理论方面均证实太阳表面磁场是自转角速度的函数(详见第4节第(1)条的讨论),即

将(8)式代入(7)式,有

式中α、k是一个常数,R0是太阳半径.因为J=IΩs,有

分别用Ω0和表示太阳目前角速度和速度变率,只要β是常数,的比值同的比值相等.由(10)式则有

取上面式子右端第2项,则β的第2个式子可写成

这样,常数β可由目前(t=0)(11)式中的Ω0和0的观测值来计算,而不能用(10)式来计算,但两个式子中的β值是相等的.

再将β代入(10)式,则(10)式可成为

将上式两端除以Ω0,则有

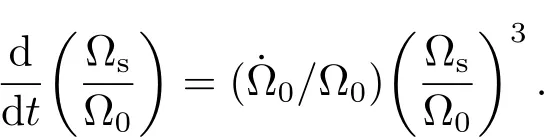
令−(Ω0/)=τ0,则上式变成的微分方程式

τ0就是太阳自转角速度维持到自转瓦解的时间,Ω0是目前角速度的值,是可知的,而0的角速度变率值由观测得到.因此τ0的值也是可知的,而文献[1]给出τ0=1010yr.

式中,Ω0是太阳目前的角速度,而Ωs(0)是太阳在主序上初始t=0的角速度,Ωs(t)是时间t的角速度.

文献[1]根据图解中角动量和质量m2/3的关系推出:太阳到达主序时,t=0为时间起点,此时太阳的自转角速度Ωs(0)=65Ω0,即角速度比目前快65倍,目前太阳自转角速度Ω0=2.865×10−5rad/s.

首先估计(13)式右端分母中第2项2t[Ωs(0)/Ω0]2/τ0的数值.太阳在主序阶段演化时间(年龄)大约为t=1×109–10×109yr,如果目前太阳的年龄取t=5×109yr,将t、τ0和代入,则得

因此,(13)式的分母第2项数值4225≫1,分母第1项的1可以略而不计.(13)式可简化成

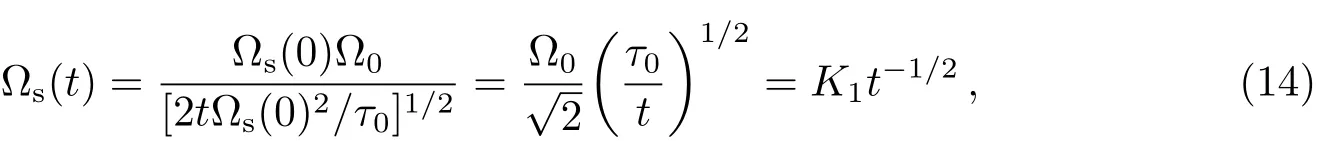
式中,Ω0=2.865×10−5rad/s,为目前太阳自转角速度,τ0=1010yr,t是从太阳到达主序开始以后的演化时标,以yr为单位.

3 对太阳在主序阶段(包括前半程和后半程)自转角速度在100亿年内在10个演化阶段演变的数值计算

根据太阳内部氢转换成氦的燃烧(核反应)太阳在主序至少停留100亿年(10×109yr).目前太阳在主序已经走完了前半程(大约50亿年),继续向后半程50亿年演化.故数值计算时可将(14)式中的时间分为10个演化阶段(1×109yr、2×109yr、3×109yr、4×109yr、5×109yr、6×109yr、7×109yr、8×109yr、9×109yr和10×109yr).将每段时间t的值和τ0=1010yr,Ω0=2.856×10−5rad/s代入(15)式,可得到太阳在主序前半程和后半程自转角速度演变的数值列入表1.

表1 太阳在主序前半程和后半程自转角速度变化的数值结果Table 1 Numerical results for the change of the rotational angular velocity of the sun in the pre-half and post-half time of the main sequence

4 讨论

关于太阳表面磁场和表面角速度到底有何关系,所得结论如下:

(1)根据文献[8]的观测,太阳磁场和自转角速度皆为时间的函数,分别为B∝t−1/2和Ω∝t−1/2.文献[21]称这种关系为Skumanich关系式.本文所得的(14)式也可以写成Ωs∝t−1/2.这从理论上证实了观测的结果是正确的.

将Skumanich的两个关系式相除,有B∝Ω,即Bs∝Ωs.这就是太阳表面磁场同表面角速度的关系,正如文献[6]所指出的:磁场本身起源于太阳发电机,它又依赖于自转角速度Ω,而文献[1]也类似地指出:磁场由太阳发电机作用产生,而它本身又是Ω的函数.此外,本文给出的理论结果同文献[1]的结果相一致.

(2)表1中给出的Ωs/Ω0的值,其物理意义就是对不同时间t的表面自转角速度为目前角速度Ω0(2.856×10−5rad/s)的倍数值.显然,Ωs/Ω0=1,即Ωs= Ω0就是目前角速度的数值.∆Ωs/Ω0就是对应不同时间角速度从初始时刻到t时刻的演变差,为目前角速度值的倍数.

(3)从表中给出的计算数值可以看出太阳质量损失在磁制动作用下使角速度随年龄逐渐减慢.从主序开始,在前半程(1×109–5×109yr)角速度开始逐渐减慢,现在Ωs(0)=Ω0=2.856×10−5rad/s,然后开始后半程(5×109–10×109yr)角速度继续减慢. 从表1中可以看到,无论主序前半程还是后半程,因质量流失和磁制动作用角速度由快逐渐变慢的演化趋势是合理的.

(4)太阳自诞生以后磁场逐渐减弱,到主序阶段仍然如此.主序前半程磁场比主序后半程较强些,故主序前半程磁制动作用比后半程强.因此,对自转角速度的制动影响前半程比后半程大些.

(5)考虑磁制动作用时,Alfven半径大于太阳半径,根据文献[6,23]的观测结果,rA≈12R,又根据(1)式和(2)式,有磁制动作用时,角动量损失率大于无磁制动作用时的损失率.故本文中的角速度变率要大于文献[13]的角速度变率.

(6)根据文献[6,24],太阳在主序前半程半径变化很小(可视为常量),而在主序后半程从5×109yr以后半径逐渐增大;当考虑质量损失对角速度影响时,由(4)式可知,当rA增大时(假定ρA和vA不变),角动量变率减小,从而角速度变率A也应减小,结果主序后半程相比前半程加快角速度变慢.

(7)根据文献[6,24],太阳在主序前半程光度变化甚微,但到后半程,从5×109yr开始光度逐渐变大.根据太阳光子辐射造成的质量损失将此代入(1)式或(2)式,角动量损失率由于光度L增大而减少从而主序后半程比前半程角速度变慢更快.然而,光子辐射对自转角速度的影响甚微.

[1]Durney B R.On theories of Solar Rotation//Bumba V,Kleczek J.Basic Mechanisms of Solar Activity.Dordrecht:Springer,1976:243

[2]Howard R.ARA&A,1984,22:131

[3]Schröter E H.SoPh,1985,100:141

[4]李林森.天文与天体物理,2013,1:45

[5]Schatzman E.The Early Stages of Stellar Evolution.Proceeding of the XXVIIIth Course of the International School of Physics “Enrico Fermi”.New York:Academic Press,1963:233-235

[6]林元章.太阳物理导论.北京:科学出版社,2000

[7]Brandt J C,Heise J.ApJ,1970,159:1057

[8]Skumanich A.ApJ,1972,171:565

[9]Barker B N.PNAS,1957,41:8

[10]Jian J,Wang J X.MNRAS,2007,377:711

[11]费森柯夫·马赛维奇.陈彪,译.天文学报,1953,1:87

[12]李林森.空间科学学报,1990,10:274

[13]李林森.天文与天体物理,2015,3:19

[14]Li L S.ARep,2016,60:853

[15]Lundquist S.ArMAF,1948,35:1

[16]Cohen O,Drake J J,Kashyap V L,et al.ApJ,2009,699:1501

[17]Brun A S.IAUS,2014,302:114

[18]Gallet F,Bouvier J.A&A,2013,556:A36

[19]Gallet F,Bouvier J.A&A,2015,577:A98

[20]Amard L,Palacios A,Charbonnel C,et al.A&A,2016,587:A105

[21]van Saders J L,Ceillier T,Metcalfe T S,et al.Nature,2016,529:181

[22]Russel C T.Solar Wind Three.Los Angeles:Institute of Geophysics and Planetary Physics,University of California,1974:231

[23]Pizzo V J,Schwenn R,Marsch E,et al.ApJ,1983,271:335

[24]Iben I Jr.ApJ,1967,147:624