小口径双管高炮身管基线修正方法
吴映锋,杨国来,李文才
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国兵器工业第58研究所,四川 绵阳 612000)
35 mm高炮是世界著名的先进高炮。我国从瑞士引进了35 mm牵引高炮,但仅是生产许可证引进,瑞士不转让其设计、计算和评价分析方法。在35 mm牵引高炮的基础上,我国又自主研制了履带式35 mm自行高炮,于是掌握其毁歼概率计算和作战效能评价分析方法的重要性更加凸显。
我国分析评价高炮武器系统的方法主要是:实测高炮武器系统发现目标的概率、跟踪目标的精度,解算未来点射击诸元的精度、随动系统精度、200 m立靶密集度、初速散布等参数。其中实测200 m立靶密集度就是测量高炮连发射击在200 m距离处立靶上留下弹孔的坐标,并假设这些弹孔坐标符合正态分布,据此计算出均方差和中间误差。通常认为立靶上的弹孔越密集,即均方差和中间误差越小,高炮的射击精度越好,毁歼概率也越高[1-5]。
对于单根身管的57 mm牵引高炮,弹孔在200 m立靶上的散布基本符合正态分布假设。通过以200 m立靶密集度代替高炮对空中目标的射击密集度,以及其他相关参数,可计算单门57牵引高炮的毁歼概率;也可以通过基线修正,计算57牵引高炮武器系统6~8门炮单一诸元(各炮身管相互平行)射击的毁歼概率。
对于双管的25 mm,35 mm,37 mm牵引高炮,由于2根平行的身管距离很近(不超过0.3 m),弹孔在200 m立靶上呈团状,无法分辨由哪根身管射出的炮弹穿过,因此仍近似认为弹孔散布符合正态分布假设。
自行高炮的总体设计与牵引高炮有很大不同。自行高炮比较重视机动能力和自主作战能力,所有分系统和单体均由同一底盘承载,其紧凑程度和集成程度较牵引高炮系统高出很多。炮塔中部易于布局的空间大多被搜索、跟踪、计算机等火控设备所占据,大多数自行高炮采用边炮布局,即偶数根炮管平行、对称地布置在炮塔外部的两侧,这样自动机排药筒和抛弹链也比较方便。
我国的425自行高炮和双35自行高炮均为边炮布局。由于425自行高炮的射击精度较差,200 m立靶上的弹孔也是一团,于是在分析评价时仍近似地作为正态分布处理。双35自行高炮的射击精度好,200 m立靶上的弹孔是局部有重叠的两团,如图1所示,其弹孔的分布已明显不是一个正态分布。所以我国传统的高炮武器系统评价方法不适用于双35自行高炮[6-9]。

图1 双35自行高炮200 m立靶上的弹孔分布规律示意图
以瑞士阿塔克(ATAK)履带式双35自行高炮为例。取两平行身管轴线间最短连线(垂直连线)的中点为原点,从原点至身管轴线的最短距离称为炮管中心距(在此情况下也就是基线)。该自行高炮两炮管的中心距为910 mm。在射击密集度趋于极限(即射击散布为0)的理想情况下,该高炮对200 m立靶连发射击应该留下相距1 820 mm的 2个弹孔,200 m立靶密集度均方差为4.76 mrad,与射击密集度相差悬殊。若对上述200 m立靶密集度不做基线修正,直接代替射击密集度用于计算毁歼概率,则计算结果肯定不合理。
还可以用反向思维的方法考察上述问题。假设能够调整在双35自行高炮炮塔两侧的身管向内倾斜,直至两身管轴线的延长线交会于200 m立靶靶面上的某一点,如图2所示。这样调整的结果必然导致两身管射击弹道交叉后又很快分开。因目标距炮口的距离通常远大于200 m,两身管射击弹道与目标平面的交会点相距甚远,所以高炮对空中目标的射击密集度较差。另一方面,因为两侧的弹道交会于200 m立靶上的同一点,留在200 m立靶上的弹孔将聚为一团,立靶密集度明显变好了。这样实际作战效果差,评价结果反而好,又从反面证明了不加身管基线修正的原有射击密集度评价方法对于边炮布局的自行高炮不合理。并且,这种两边炮的身管以较大角度向内倾斜的情况是不允许的。
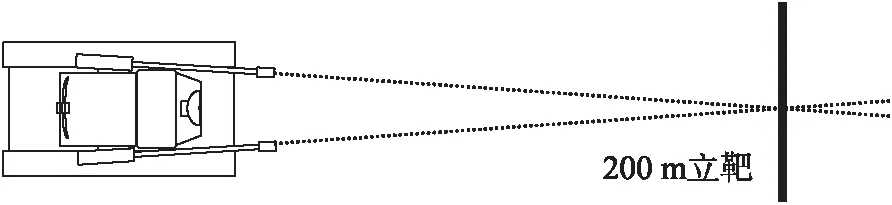
图2 身管向内倾斜的弹道示意图
实际上,边炮布局自行高炮的炮管中心距均不超过1 m。在高炮系统作战时,目标距离不仅远超过200 m,而且目标也有一定的尺寸,对于如此小的炮管中心距,本来不应该存在基线修正的问题。问题其实出在评价方法上,所以有必要修改传统的射击密集度评价方法。
1 连发射击200 m立靶散布的密度函数
高炮连发射击在200 m立靶上留下弹孔的分布密度函数公式为
(1)
式中:X=(x1x2),为射击误差的二维随机向量;Σ是二维随机向量X的协方差矩阵,|Σ|是方差;A=(a1a2),为二维随机向量X的数学期望E[X],a1,a2分别是高炮连发射击精度中的方位误差和高低系统误差。因为偏流和横风等因素对35炮200 m立靶射击密集度的影响很小,A主要取决于跳角。
从图1可看出,双35自行高炮的200 m立靶射弹散布可认为是2个对称的二维正态分布之和的分布,即每根身管的射弹散布服从一个二维正态分布。这2个对称二维正态分布的数学期望分别为A-A1和A-A2,即A-A1和A-A2分别为2根身管的射弹散布中心,A1和A2分别是双管高炮200 m立靶射击2个散布中心距离单管35散布中心的距离向量。|A1|=|A2|=a,可认为是2根身管的中心距,即A1+A2=0。2个协方差矩阵均为Σd。
第1根身管连发射击200 m立靶散布的密度函数为
(2)
记
(3)
将式(2)展开:
(4)
同理,第2根身管连发射击200 m立靶散布的密度函数为
(5)
2 身管射弹散布方差
设每根身管发射n发炮弹,第1根身管发射的弹丸编号为1,…,n;第2根身管发射的弹丸编号为n+1,…,2n;Xi表示第i发弹在立靶上弹孔位置的随机变量。则
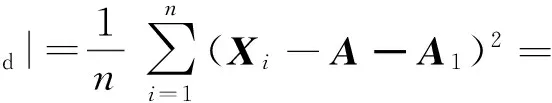
(6)
同理,第2根身管射弹散布的方差:

(7)
将式(6)和式(7)取平均,得:
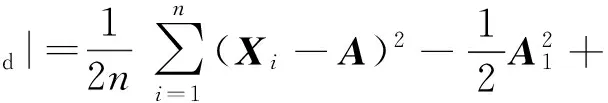
(8)
由于200 m立靶上弹孔散布的方差|Σ|为

(9)
代入式(9),可得:

(10)
利用式(10)就可以根据200 m立靶射击的试验结果换算出35 mm自行高炮拦截空中目标的对空射击密集度。
为了工程上的方便,常以方位和高低均方差表示射击密集度:
(11)
式中:σd,x,σd,y是协方差矩阵Σd内的对应元素;σx,σy是协方差矩阵Σ内的对应元素。
3 总结和推论
根据200 m立靶连发射击的试验结果,可计算出方差|Σ|和数学期望A;根据双35自行高炮的身管中心距a,可确定2根身管连发射击的数学期望A-A1和A-A2。再通过方差|Σ|和身管中心距a,利用式(10)可确定各身管射弹的二维正态分布方差|Σd|,再由实测的高炮武器系统跟踪目标精度、解算的未来点射击诸元精度、随动系统精度和初速散布等参数,就可以利用计算57牵引高炮武器系统毁歼概率的方法来计算双35自行高炮的毁歼概率。
仍以瑞士阿塔克双35自行高炮为例。该高炮身管中心距为0.91 m,反映到200 m立靶处为4.76 mrad。处理200 m立靶连发射击的试验结果,记靶面上弹孔水平方向散布为Dx,垂直方向散布为Dy,如图3所示。

图3 200 m立靶弹孔分布
计算结果为方位5.02 mrad,高低1.58 mrad。代入式(10)可算出单管连发射击密集度的均方差为
(12)
将身管数量、中心距、单管连发射击密集度以及其他相关参数输入标准的毁歼概率计算软件,就可算出阿塔克双35自行高炮的毁歼概率。这样,就可以用200 m立靶密集度代替对空射击密集度的传统方法,获得能够正确评价双35自行高炮对空射击密集度的新方法。
为建立双35自行高炮对空射击密集度的定量概念,本文给出一个近似估算。假设阿塔克双35自行高炮射击斜距离2 500 m处的目标,射弹散布如图4所示。
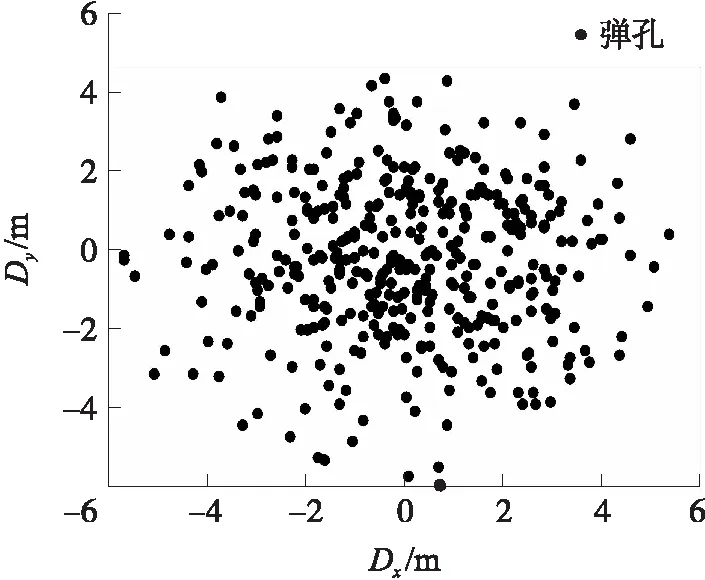
图4 斜距2 500 m射弹散布


表1 本文方法与传统分析结果的对比
表1中,σd,x,σd,y分别表示方位散布与高低散布均方差。可见,采用本文身管基线修正方法,修正后200 m立靶计算的密集度与2 500 m密集度相近,修正后可以用200 m立靶密集度对双35对空射击密集度进行评价。

推论以上结论可以拓展到多管自选火炮,假设某自行高炮有k根相互平行的身管,则利用200 m立靶密集度数据计算该多管火炮对空射击密集度的公式如下:

(13)
式中:Ai为第i根身管的中心距反映到200 m立靶上的二维向量。
[1] 肖元星,张冠杰. 地面防空武器系统效费分析[M]. 北京:国防工业出版社,2006.
XIAO Yuanxing,ZHANG Guanjie. Analysis of the efficience and cost of ground air defense weapon system[M]. Beijing:National Defense Industry Press,2006. (in Chinese)
[2] 刘顺利,王玉生. 防空兵射击理论与射击指挥[M]. 北京:解放军出版社,2000.
LIU Shunli,WANG Yusheng. Firing theory and control of air defense[M]. Beijing:PLA Publishing House,2000. (in Chinese)
[3] 马春茂,陈熙,侯凯,等. 弹炮结合防空武器系统总体设计[M]. 北京:国防工业出版社,2008.
MA Chunmao,CHEN Xi,HOU Kai,et al. The overall design of the missille gun combined with air defense weapon[M]. Beijing:National Defense Industry Press,2008. (in Chinese)
[4] 倪忠仁,张宪复,段梦钤,等. 高炮射击理论[M]. 北京:中国人民解放军总参谋部炮兵部,1986.
NI Zhongren,ZHANG Xianfu,DUAN Mengquian,et al. The theory of artillery shooting[M]. Beijing:PLA Army General Staff Department,1986. (in Chinese)
[5] 潘承泮. 武器系统射击效力[M]. 北京:兵器工业出版社,1994.
PAN Chengpan. Weapon system shooting effectivenss[M]. Beijing:Ordnance Industry Press,1994. (in Chinese)
[6] 王宝元,衡刚. 火炮立靶密集度测量方法[J]. 测试技术学报,2011,25(6):529-535.
WANG Baoyuan,HENG Gang. The measurement methods for vertical target dispersion of gun[J]. Journal of Test and Measurement Technology,2011,25(6):529-535. (in Chinese)
[7] 王广伟,芮筱亭,王国平. 武器弹药立靶密集度试验方法研究[J]. 南京理工大学学报,2006,30(4):482-485.
WANG Guangwei,RUI Xiaoting,WANG Guoping. Test method for vertical target dispersion of ammullition[J]. Journal of Nanjing University of Science and Technology,2006,30(4):482-485. (in Chinese)
[8] 彭峰生,廖振强,王涛. 有脱靶弹时多管火炮立靶密集度估计[J]. 弹道学报,2008,20(1):66-69.
PENG Fengsheng,LIAO Zhenqiang,WANG Tao. Vertical target density estimation of multi-barrel automatic gun with a few of missing projectiles[J]. Journal of Ballistics,2008,20(1):66-69. (in Chinese)
[9] 贠来峰,史初蕾,王建国. 某炮弹立靶密度集度的影响因素分析[J]. 弹道学报,2009,21(4):13-16.
YUN Laifeng,SHI Chulei,WANG Jianguo. Analysis on factors influencing vertical target dispersion of projectile[J]. Journal of Ballistics,2009,21(4):13-16. (in Chinese)

