一种面向设备维修时间预测的组合优化模型及其应用∗

谢 浩 万振刚

1 引言

由于设备维修时间受到运行状态、运行年限、工作环境等多种因素的影响，简单的灰色预测模型已经不能准确地描述设备维修的时间序列规律。为了得到更准确的预测模型，人们把灰色模型与其他模型结合形成新的方法，如：张俊深等提出了基于BP神经网络与修正灰色预测模型［1］，并运用于能源消耗预测，但该模型对数据量的要求较高，往往需要多指标因素集，训练时间较长；陈华友等提出了基于灰色关联度的组合预测模型［2］，但该模型建模过程比较复杂，多应用于数据存在一定冗余的场合；候丽敏等提出了基于灰色线性回归组合模型［3］，并运用于铁路客运量预测，但该模型并没有从本质上解决求解参数最优解的缺陷。

本文首先采用混沌粒子群算法优化灰色模型参数，然后结合适用于短期预测的线性回归方法，推导得到可以补偿灰色预测模型误差的设备维修时间预测模型，同时利用船用柴油机汽缸活塞间隙历史数据进行了仿真模拟，其预测结果比以往简单的灰色预测模型预测精度有较大的提高。

2 设备维修时间灰色预测模型

灰色预测模型是一种纯指数模型，其优点就是建模过程中对数据的要求量少，计算简单，短期预测有较高的拟合精度，运用领域广等，以上优点符合设备维修时间贫信息短期预测的要求。基于灰色预测模型的优点，刘爱华运用简单的灰色预测模型对船舶柴油机维修时间进行预测［4］。但预测结果都存在较大误差，在分析灰色预测模型和数据序列的基础上，总结出误差较大的主要原因有：首先没有考虑灰色预测模型在求解过程中发展灰度和内生控制灰度两个参数不是最优解的干扰，其次没有充分考虑设备所处运行状态、运行年限、工作环境等多种因素引起的数据序列波动。

3 组合优化模型

本文选取船舶柴油机维修时间预测作为研究对象，根据灰色预测模型的缺点和设备异常数据序列并不可能完全符合指数规律的特性，利用混沌粒子群算法优化灰色模型参数，并在此基础上，结合线性回归补偿方法，推导得出一种面向设备维修时间预测的组合优化模型。

3.1 灰色预测模型参数优化

针对灰色预测模型求解参数不是最优解的缺陷［5］，本文引入混沌粒子群优化算法进行灰色预测模型参数的优化。

粒子群优化算法［6］通过多次判断粒子所处的位置和速度，根据适用度方差和平均粒距的大小寻找最优解，其搜索效率较高，收敛速度较快，但在搜索过程中，会因为部分粒子比较靠近全局最优解而产生多个局部最优解，从而干扰全局最优解的搜索。混沌寻优算法［7］作为一种运用在非线性规律上的方法，比大多数随机寻优算法更可靠，混沌状态引入到优化变量的思路是：在优化变量的范围内实现混沌粒子的随机遍历，利用混沌变量进行搜索。

混沌粒子群优化算法实现了上述两种算法的优势互补，可以解决灰色预测模型参数发展灰度和内生控制灰度求解过程中不易找到最优解的缺陷，达到优化参数的目的。

3.2 模型误差线性补偿

在设备维修时间历史序列中，很多序列存在数据波动，而灰色预测模型主要适用于指数增长型数据序列，并没有包含数据波动所引起的误差，为此，本文在优化参数的基础上进一步增加线性补偿环节，使得最终所得到的组合优化模型适用于既含有指数增长又包括线性增长的序列，从而减小数据序列波动所带来的预测误差，为设备维修时间预测提供更加准确、可靠的计算模型［8］。

3.3 算法流程

组合优化预测模型的建模过程如图1。

图1 组合优化预测模型的建模过程

建立组合优化预测模型建模步骤如下。

步骤1：灾变序列的提取。收集设备状态偏离阀值的数据，把大于阈值数据提取出来构成上灾变异常序列x（0），同理也可以根据需要构成下灾变异常序列：

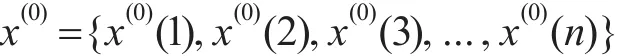
步骤2：灰色G（1，1）模型建立［9］。其中建立的白化方程为

步骤3：灰色预测模型参数优化。式（1）中a为发展灰数，b为内生控制灰度，均为未知参数，反映了数据间的变化关系。原灰色预测模型通过最小二乘法进行参数求解，求解的参数不能达到最优解，从而产生预测误差，现参数a、b来源于混沌粒子群优化算法优化求解表达式，其中 x^(t)是式（1）偏导数的解，当F处在最优解时，对应速度矢量的横坐标为a、纵坐标为 b，基本的优化模型［11］如下：给予粒子初始化随机速度和位置，通过粒子速度更新算法Vid：式（2）和粒子位置更新算法xid：式（4）分别进行粒子速度和位置更新，其中，在基本粒子群位置算法上引入了混沌扰动，以增加粒子的多样性，式（3）为混沌变量Cid，是衡量粒子的混沌程度。与以往的粒子群优化灰色模型参数不同，本次混沌扰动变量与粒子群处在交替的运动过程，使得收敛速度更快，而以前的改进思路是在粒子群陷入局部最优解之后引入混沌状态，取代原粒子位置。

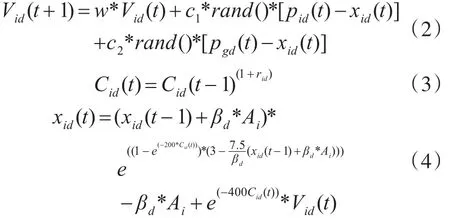
其中，w为惯性权重；c1、c2均为学习因子；pid为局部最优位置；pgd为全局最优位置；rid是一个小于1的常量，表示第i个粒子的第d维混沌因子；t为迭代次数；βd为搜索测度；Ai为粒子i在搜索空间内向负方向的比例，如：βd=1000，Ai=0.3，则表示搜索空间为［-300，300］。

将优化后的参数a、b值代入式（1），通过式（1）求解的离散化形式为

步骤4：模型误差线性补偿。优化参数后解的离散化形式属于纯指数规律，没有考虑数据本身含有的数据波动，为此进行线性回归补偿。基于线性回归的基本模型 y=a1x+b1和指数的基本模型y=a2ex来拟合生成累加序列

步骤 5：参数求解［12～13］。

设 L(k)=evˉk，那么式（7）可以表示为

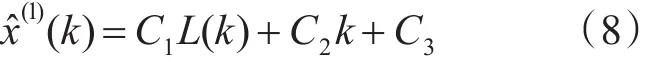
取不同的m值，把平均值作为v的估计值：

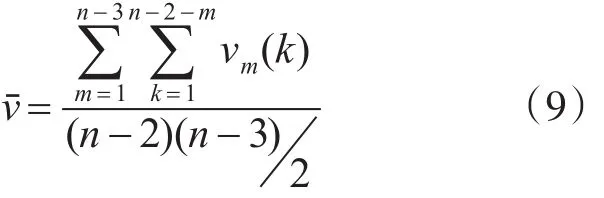
运用式（10）来求解估计值C1，C2，C3。

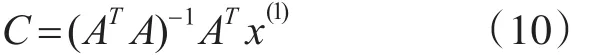
其中

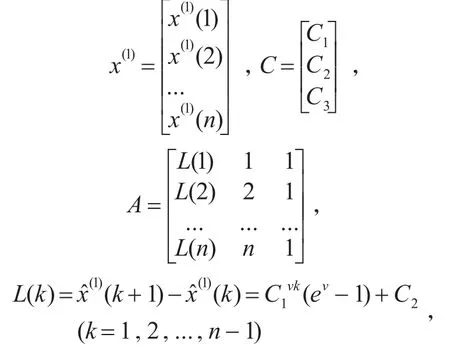
步骤6：预测结果求解。通过步骤5的求解参数发现：在C1=0的状况下，设备异常点变化的规律适应于完全线性模型；在C2=0的状况下，设备异常点变化的规律适用于完全指数规律，符合基本的灰色预测模型；在C1，C2都不等于0的状况下，设备异常点变化的规律适用于本文研究的组合优化模型。把参数带入式（11）得

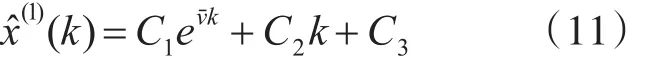
对式（12）得到的序列进行累减还原即

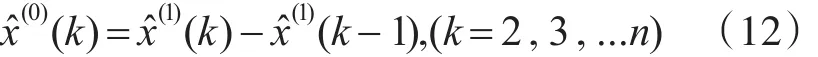
其中当k=1时，x^(0)(1)=x^(1)(1)

4 案例分析

以某船柴油机汽缸——活塞间隙测量数据为例进行算法预测精度的比较，来确定下一次维修时间。每日汽缸——活塞间隙测量数据［4］，间隙单位：mm；序号单位：天。

本数据来源人工测量，根据设备性能要求，当测量值大于0.40mm时处在异常状态，因此汽缸活塞间隙的上限阈值为0.40mm，将大于0.4mm的异常点截取出来，构造上灾变序列，其中x代表需要维修的具体天数，如表1。

表1 异常数据序列

首先选取前七次的异常序列作为训练数据来预测第八次需要维修的时间。

基本的灰色预测模型是通过最小二乘法求解发展灰度和灰色作用量［11］，解为a=-0.2804；

b=13.125，即灰色预测模型为式（13）：

在原灰色预测模型预测结果的基础上添加线性补偿［3］，即灰色线性回归组合模型为式（14）：

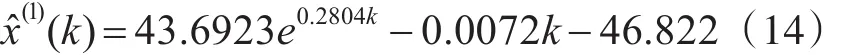
而本文组合优化模型中参数设置为w=0.714，C1、C2均为 2，粒子个数 N=7，T=1500，r（i，d）=0.5+（0.005）rand，Cid（t）=0.99，βd=10.3，Ai=0.5，按步骤3思路求解，结果为：a=-0.282；b=13.1514，参数优化后灰色预测模型生成最新序列。首先通过步骤5求解参数，然后带入式（11），即组合优化模型为式（15）：

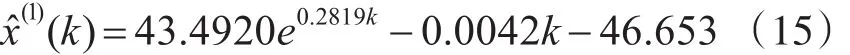
利用三种模型绘制拟合曲线如图2。从图中可以直观地看出组合优化模型拟合曲线的第8次预测绝对误差相对较小，更接近真实值。

同理，分别选取前五次、前六次的异常序列作为训练数据来预测下一次需要维修的时间，三次选取训练数据对应最终的维修时间预测结果如表2。

通过表2发现，组合优化模型的预测结果更加贴近真实值，而且训练数据越多，组合优化模型的预测精度越高。

综上所述，本文研究的组合优化模型对于柴油机汽缸的维修时间预测精度更高。

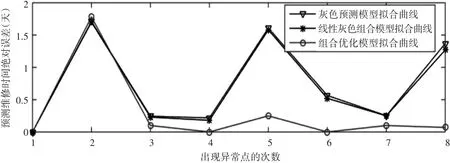
图2 三种模型拟合曲线

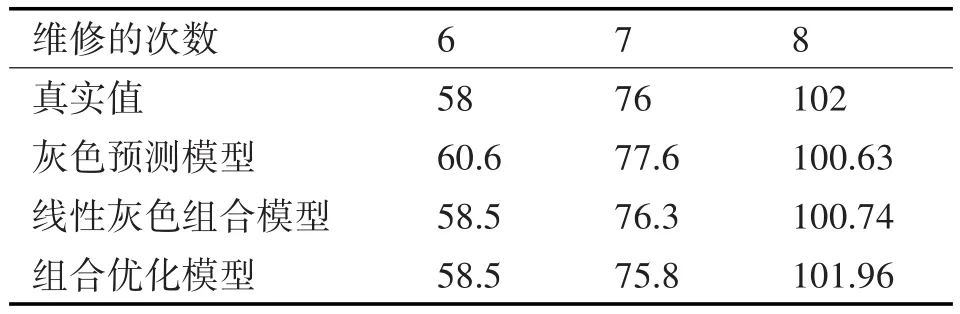
表2 三次维修时间预测结果

5 结语

利用混沌粒子群优化算法估计灰色模型参数，然后结合线性回归方法推导得到可以补偿灰色预测模型误差的设备维修时间预测模型，建立了柴油机汽缸活塞运动的间隙对应异常值预测模型，通过仿真曲线的走势、预测结果与真实数据的误差，得到组合优化模型拟合精度好，误差小，预测结果更贴近真实值，能够反映柴油机汽缸活塞运动异常点的发展趋势，具有较高的应用前景。因此，本文改进的组合优化模型用于柴油机汽缸活塞运动的间隙异常值预测是可行的，并且能够获得足够的预测精度，为柴油机视情维修提供较大的指导意义，推进了设备视情维修的发展。

［1］张俊深，袁程炜.基于BP神经网络与修正灰色预测模型的能源消耗组合预测［J］.统计与决策，2016（5）：90-93.

［2］陈华友，赵佳宝，刘春林.基于灰色关联度的组合预测模型的性质［J］.东南大学学报（自然科学版），2004，34（1）：130-134.

［3］候丽敏，马国峰.基于灰色线性回归组合模型铁路客运量预测［J］.计算机仿真，2011，28（7）：1-3.

［4］刘爱华.基于CWBT的管理信息系统研究［J］.武汉理工大学，2005（7）：3-5.

［5］姚天祥，巩在武.灰色预测理论及应用［M］.北京：科学出版社，2014（5）：43-46.

［6］MI Solihin，LF Tack，ML Kean.Tuning of PID Controller Using Particle Swarm Optimization（PSO）［J］.Iranian Journal of Electrical&Electronic Engineering，2011（3）：1-4.

［7］李文，伍铁斌，赵全友等.改进的混沌粒子群算法在TSP中 的 应 用［J］.计 算 机 应 用 研 究 ，2015，32（7）：2065-2067.

［8］卢阳.基于灰色线性回归组合模型的金融预测方法［J］.统计与决策，2017（10）：91-93.

［9］邓聚龙.灰预测与灰决策［M］.武汉：华中科技大学出版社，2002（9）：81-82.

［10］盖兆梅，付强，刘仁涛，基于混沌粒子群优化算法的灰色GM（1，1）模型在地下水埋深预测中的应用［J］，数学的实践与认识，2008 ，38（11）：69-74.

［11］胥小波，郑康锋，李丹等.新的混沌粒子群优化算法［J］.通信学报，2012，33（1）：24-30.

［12］TGao，BGao.Failure rate prediction of substation equip⁃ment combined with grey linear regression combination model［C］//EEE International Conference on High Volt⁃age Engineering and Application，2016（3）：1-5.

［13］GAN JianSheng，CHEN GuoLong.Linear Combination Forecasting Model and its Application［J］. 计 算 机科学，2006，33（9）：191-194.