基于IPSO-BP神经网络的跟踪微分器∗

王 坤

1 引言

无论在传统的PID控制器的设计中，还是在信号处理与分析领域中，常常需要对测量到的信号进行求微分处理。由于理想微分器是物理不可实现的，在工程实际中往往采用一阶比例微分环节或采用惯性环节来近似代替微分变换提取微分信号。但利用惯性环节进行微分信号提取时，必须将惯性环节的时间常数设置的很小，时间常数越小，微分信号的逼近精度越高，但同时由于时间常数过小，使得噪声放大效应越明显，严重时甚至会淹没真正有用的微分信号。对此，中国科学院系统所的韩京清研究员提出了一种有效地获取一阶微分信号的方法—跟踪微分器（Tracking Differentiator，TD）。跟踪微分器是自抗扰控制技术中的重要组成部分，利用它不仅能较好地复现系统的状态信号，而且还能够得到较为满意的一阶微分信号［1］。此外，通过多个跟踪微分器的直接级联还可以获得二阶甚至更高阶的微分信号，因而得到了工程应用领域的广泛关注［2～5］。文献［6］从二阶系统的时间最速控制出发，建立了基于符号函数的跟踪微分器的数学模型。但由于所构造的函数是非光滑、非连续的，在控制过程中会因切换而产生抖动，跟踪和微分效果不够理想，且收敛速度较慢。针对此问题，文献［7～8］构造了离散形式的最速跟踪微分器，并在极值点附近设置线性区域以消除抖动。文献［9～11］在此前研究的基础上，从构造的综合控制函数出发，又对跟踪微分器的数学模型进行了一系列的改进，提出了不同形式的数学模型。但是在这些文献里所建立的跟踪微分器的数学模型中存在一个共同的问题，就是在其数学模型的表达式中含有多个未知的待定参数，而这些参数的取值将直接影响到跟踪微分器输出的跟踪信号以及其一阶微分信号的精度。

为此，本文以跟踪微分器常见的时间连续形式和离散形式的数学模型为研究对象，将粒子群优化算法及非线性系统神经网络建模的思想引入跟踪微分器的未知参数整定问题，提出了基于改进型粒子群算法的BP神经网络建立跟踪微分器数学模型的设计方法。通过对单个和级联的跟踪微分器系统的仿真，表明利用该方法设计的跟踪微分器具有良好的动态响应，得到的各阶次“微分信号”的精度较高，并且利用文中所提出基于IPSO-BP神经网络设计出的跟踪微分器还具有较强的鲁棒性。

2 跟踪微分器

跟踪微分器是一个动态的滤波、求导系统。输入控制系统的状态信号v(t)，它将输出两个信号x1(t)，x2(t)，其中x1(t)是对输入信号v(t)的跟踪与复原，x2(t)是x1(t)的微分，即为v(t)的一阶微分信号x2(t)≈v˙(t)。由跟踪微分器得到的微分信号是输入信号广义导数的一种光滑逼近。

为了验证本文算法的正确性，在此给出两种非线性跟踪－微分器的具体形式［6～8］。

2.1 连续时间数学模型

由二阶最速开关系统，可以得到二阶时间连续跟踪－微分器的数学模型为

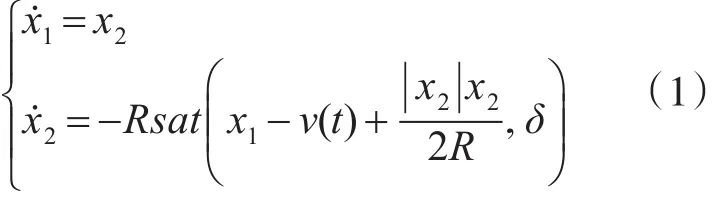
其中

时间连续形式的跟踪-微分器是根据二阶系统的时间最优控制得到的，具有良好的快速性。通过在开关线附近添加适当线性区域会更进一步改善输出信号的性能，减小颤振，得到比较好的跟踪和微分效果性。

2.2 离散时间数学模型

为了消除原点附近的颤振，提高系统的稳态精度，改善系统动态响应特性，在大量的研究基础上，提出了跟踪微分器的离散形式。跟踪-微分器的离散形式如下

通过上面的分析可以看出，跟踪-微分器连续时间形式的数学模型中，参数R，δ为未知参量。跟踪-微分器离散时间形式的数学模型中，参数h，r也是待定的未知参数。而这些参数的取值是否合适，将直接影响到跟踪-微分器获取精确跟踪和微分信号的效果。

3 基于IPSO算法的BP神经网络

3.1 BP神经网络

人工神经网络是以工程技术手段从微观结构与功能上对人脑神经系统的模拟而建立起来的一类非线性模型，具有模拟人的部分思维的能力，其特点是具有非线性特性、学习能力和自适应性，是模拟人的智能的一条重要途径。它由简单信息处理单元互连组成网络，能接收并处理信息。神经网络的信息处理由处理单元之间的相互作用来实现，它是通过把问题表达成处理单元之间的连接权来处理的。

BP神经网络是一种静态自学习前馈逼近式网络，具有很强的学习功能，由于其自身所具有的信息分布式存储和并行处理的特点，使其被广泛地应用于模式识别，非线性系统辨识等领域。尽管在很多控制工程领域取得了很大的成功，但是BP神经网络仍然存在着一些问题，主要表现在两个方面，一是BP网络的训练时间长，学习算法收敛慢，甚至不收敛，出现训练失败的问题；二是BP网络所采用的梯度下降的修正算法，使网络易陷入局部极值，并且无法逃离局部极值点。因此近年来BP网络的优化成为了BP网络研究的重点之一。

3.2 改进粒子群算法

粒子群算法由电气工程师R.Eberhart和美国心理学家Kennedy共同提出，通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。在粒子群算法中，搜索空间内的每个粒子都代表一个可行解，利用适应度函数可以求出种群中所有粒子的适应值。根据计算得到的适应度值，粒子依据当前最好的个体值和群体中所有粒子的最优值，更新自身的位置与速度，直到找到适应度函数最小的最优值时停止更新。每个粒子的速度和位置按下述公式进行更新［12］：

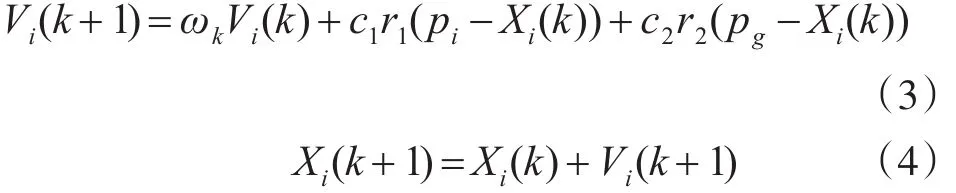
式中，Xi表示第i个粒子在空间中的位置向量；Vi表示第i个粒子的飞行速度向量。

第i个粒子搜索到的历史最优位置表示为pi，整个群体搜索到的最优位置表示为 pg，它是所有pi中的最优值。ωk称为惯性权重，通常在[0，1]之间取值，它表示使微粒保持运动惯性的能力，使其具有扩展搜索空间的趋势。c1和c2为实常数，称之为加速度系数，表示将每个粒子推向个体最优解和全局最优解的统计加速度的权重，用于调节该粒子向自身已寻找到的最优位置和同伴已寻找到的最优位置方向飞行的最大步长；r1和r2为[0，1]之间的随机数。

粒子群算法采用直接寻优的原理，这使得其收敛速度要比遗传算法等优化算法速度要快，但是这也导致算法存在容易早熟收敛等缺点，为此在本文中采用可变惯性权值的方法，改善现有算法性能。

惯性权重表示粒子现有速度对先前速度的取舍程度，当惯性权重较大时有利于粒子群在全局范围内进行搜索，而当权重值较小时将更有利于粒子群进行局部搜索，但陷入局部极小的可能会大大增加。综合考虑惯性权重的全局和局部的搜索能力，在寻优的过程中按照式（5）不断调整惯性权重系数值。

式中，ωmax表示惯性权重系数的最大值，通常在0.8～1.2之间取值，ωmin表示权重系数的最小值，通常取为0.4。Ma xk表示最大迭代次数，k表示当前迭代次数。

3.3 基于IPSO算法的BP神经网络

将改进型粒子群优化算法的思想引入到BP神经网络的训练中，用改进后的粒子群优化算法替代误差反向传播算法中的梯度修正，可以实现缩短网络训练时间，提高网络收敛精度的目的。具体的训练方法是，用粒子群中的每个粒子的位置表示BP网络中所有待定权值和阈值的集合，每个粒子的维度由BP网络的结构所决定，即维数等于BP网络中的权值与阈值的数量之和。以给定训练样本的BP神经网络的输出误差的均方函数作为IPSO算法的适应度函数，其数学表达式如式（6）所示。

适应度函数值反映了神经网络的训练误差，适应度值越小则说明粒子在搜索过程中，使得BP网络所建立的非线性映射关系与实际非线性函数的吻合度越好。

利用IPSO算法训练BP神经网络的算法流程图如图1所示。

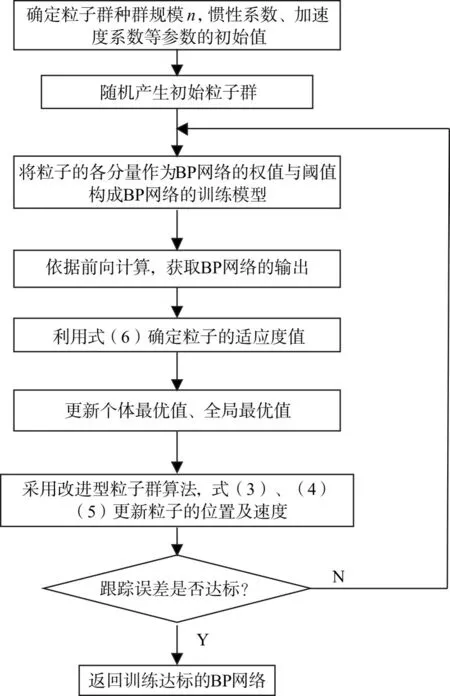
图1 基于IPSO算法的BP网络训练流程图

4 基于IPSO-BP神经网络的跟踪-微分器

由跟踪微分器的数学模型（1～2）可见，连续时间模型中的待定参数R和δ或离散时间模型中的待定参数h和r都将直接影响跟踪微分器的输出量x1(t)，x2(t)的形式及精度。因此，为了确定模型中的待定参数，将神经网络建立非线性系统数学模型的思想引入参数整定，提出基于IPSO-BP神经网络建立跟踪微分器数学模型的设计方法。

从跟踪微分器数学模型的表达式可以看出，模型中的未知参数与模型输出信号之间可以被视为一种特殊的非线性映射，因此可以利用非线性的神经网络建立该映射，从而建立未知参数与输出信号之间的对应关系。具体的做法是，首先给定一组未知参数，通过龙格库塔算法求解一阶微分方程组，得到一组与未知参数相对应的跟踪信号和一阶微分信号，将跟踪微分器的输出信号与未知参数之间构成一组训练样本。选取多组未知参数，采用同样的算法，即可获得训练样本集。接下来，利用所获取的训练样本集对基于IPSO-BP神经网络加以训练，训练结束时，所构造的IPSO-BP网络将建立跟踪微分器的输出信号与未知参数之间的非线性数学关系。最后，将理想的跟踪信号及其一阶微分信号输入神经网络，即可确定未知参数值，从而达到设计跟踪微分器的目的。以连续时间形式的数学模型的设计为例，给出基于IPSO-BP网络的TD中待定参数确定的算法流程图，如图2所示。

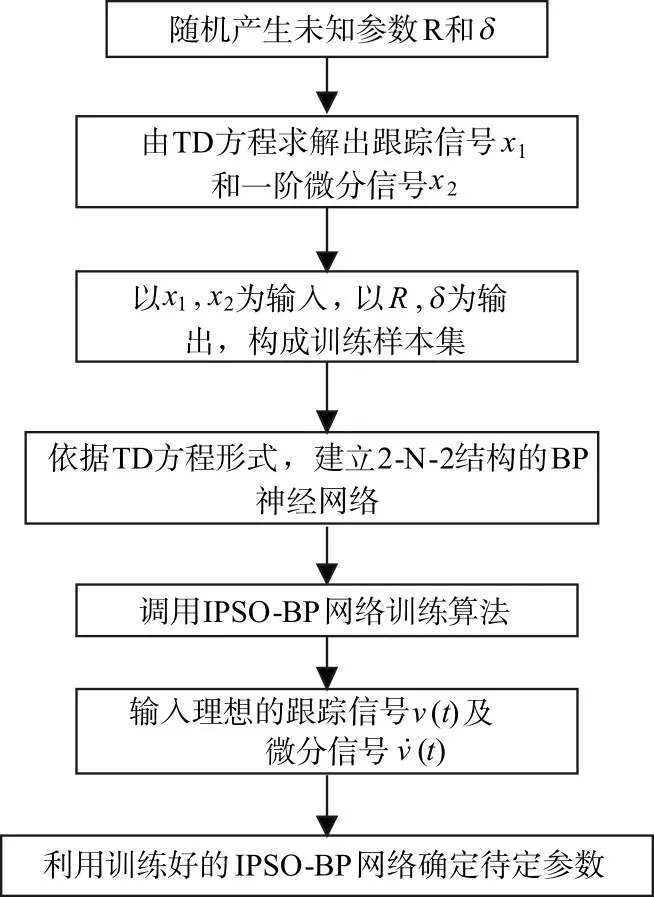
图2 跟踪微分器未知参数整定算法流程图

5 仿真结果与分析

为了验证文中所提出的基于IPSO-BP神经网络的跟踪-微分器设计方法的正确性，以单个跟踪微分器的常用连续形式和离散形式的数学模型为研究对象，采用连续可微的信号为输入量，分别给出了单个跟踪微分器的跟踪输出及一阶微分信号输出，并在不改变跟踪微分器待定参数的前提下，通过两个跟踪微分器的直接级联获取原有输入信号的二阶微分信号，由此来验证利用文中所提出的方法设计的跟踪微分器具有较好的鲁棒性。

为了便于分析比较，文中采用的输入信号的形式为

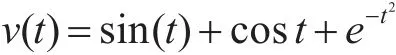
仿真结果如下：

1）连续时间的跟踪-微分器

根据文中的设计方法，首先设计一级跟踪微分器的数学模型，仿真结果如图3所示。

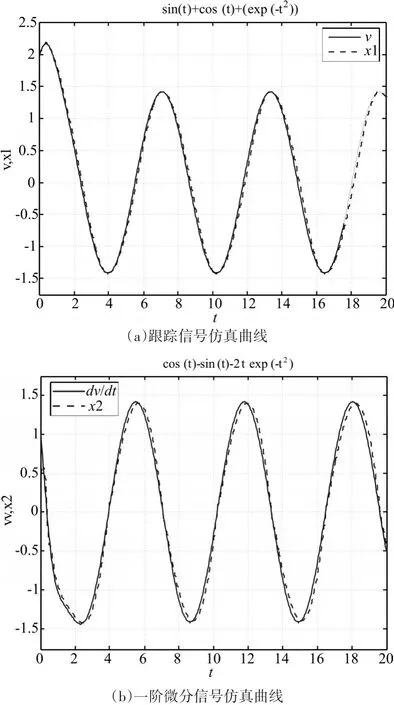
图3 一阶跟踪微分器仿真图

由仿真图3可见，采用文中设计方法所构造的跟踪微分器能很好的给出原有信号的跟踪信号及其一阶微分信号，跟踪误差达到1.6×10-7。

为了验证参数设计方法的有效性以及由该算法所得到的待定参数的鲁棒性，将两个相同的跟踪微分器直接级联，由第二个跟踪微分器直接获取原有输入信号的二阶微分信号，仿真曲线如图4所示。

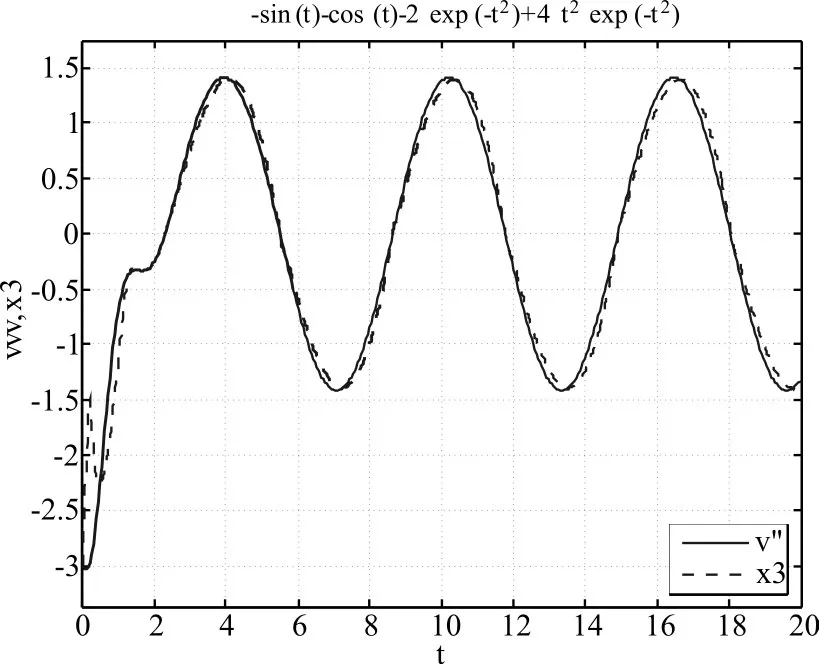
图4 二阶微分信号仿真曲线

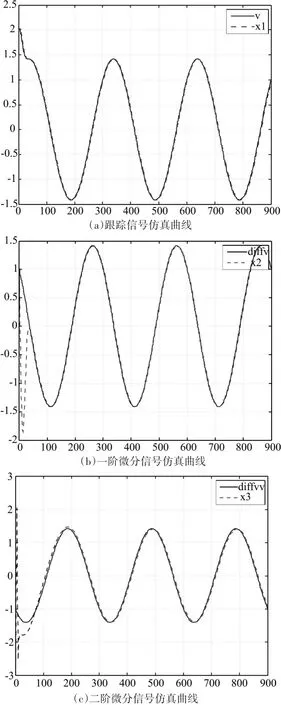
图5 离散形式跟踪微分器仿真图

从仿真图3和图4可以看出，采用文中所提算法设计的跟踪微分器不但能获取较高精度的一阶微分信号，而且仅通过直接级联的方式就可以获取二阶微分信号，并且其精度也较高。

2）离散时间的跟踪-微分器

按照相同的设计方法，利用IPSO-BP神经网络训练获取离散形式的跟踪微分器中的未知参数。为了便于比较，仍先设计一级跟踪微分器的数学模型，再通过直接级联的方式获取高阶的微分信号。仿真结果如图5所示。

从仿真图5中可以看出，文中所提出的设计方法同样适用于跟踪微分器离散模型的设计，仍可以得到高精度的跟踪、一阶微分信号和二阶微分信号。但同时也应注意到，由两个TD串联后得到的二阶微分信号在初始时间段内，产生了明显的震荡，这主要是由于离散结构形式在生成高阶微分信号时，会产生随机噪声。因此，在实际使用离散形式的高阶跟踪微分器时，应避开第一个周期，从第二个周期开始提取微分信号。

6 结语

本文在对跟踪微分器的连续时间和离散时间形式的数学模型研究的基础上，结合前馈型神经网络建立非线性系统数学模型的原理，提出了基于IPSO-BP神经网络的跟踪微分器的设计方法。通过对一级、二级连续时间和离散时间的跟踪微分器系统的仿真表明，该算法不仅可以获得高精度的系统跟踪信号和一阶微分信号，而且通过简单的直接级联的方式还能获取较高精度的二阶微分信号。此外，文中所提出的参数整定算法具有一定的扩展性，可以用于其他形式的跟踪微分器数学模型的设计。

［1］韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术［M］.北京：国防工业出版社，2009：59-79.

［2］张海丽，张宏立.微分跟踪器的研究与应用［J］.化工自动化及仪表，2012，40（4）：474-477.

［3］付瑞玲，李文方.跟踪微分器在生物雷达中的应用［J］.自动化技术及应用，2014，33（3）：59-61.

［4］Jin Longxu，Zhang Ke.The Application of Tracking Differ⁃entiator in Variable Speed Servo Control System［J］.2nd International Conference on Intelligent Materials and Me⁃chatronics，2015，IMM 2015：91-95.

［5］Li Xiaoqi，Wang Wei，Yi Jianqiang.Stable Transition of Quadruped Rhythmic Motion Using the Tracking Differen⁃tiator［J］，Journal of Harbin Institute of Technology，2015，10：9-16.

［6］韩京清，王伟.非线性跟踪-微分器［J］.系统科学与数学，1994，14（2）：177-183.

［7］韩京清，袁露林.跟踪微分器的离散形式［J］.系统科学与数学，1999，19（3）：268-273.

［8］孙彪，孙秀霞.离散系统最速控制综合函数［J］.控制与决策，2010，25（3）：473-477.

［9］史永丽，侯朝桢.改进的非线性跟踪微分设计［J］.控制与决策，2008，23：647-650.

［10］程春华，胡云安，吴进华.输入非仿射不确定系统的跟踪控制［J］.系统工程与电子技术，2014，36（2）：354-360.

［11］谢云德，李云钢，佘龙华.一种基于边界特征线的二阶非线性离散跟踪微分器［J］.信息与控制，2014，43（3）：257-263.

［12］王坤，张立广，王琪.基于改进型粒子群算法的扩张状态观测器［J］.国外电子测量技术，2017，36（08）：66-70.