基于光学检测方法的霍普金森压杆技术综述

杨山伟

摘 要：分离式霍普金森压杆技术是一种被广泛应用于测量材料在高应变率范围内动态力学性能的一种行之有效的实验手段。传统的霍普金森压杆测量方法主要是利用粘贴在入射杆和透射杆上的应变片实现对被测材料动态力学性能测量的目的，但是这种应变片式的霍普金森压杆技术中仍存在一些固有的问题和不足。为了获得更高效、精确的实验数据，基于光学检测方法的霍普金森压杆测量技术应运而生。它具有非接触性、高度可重复性、测量结果更加可靠和准确等优点。文章首先简要回顾了传统分离式霍普金森压杆技术的起源与发展，以及测量装置和测量原理。在此基础上，重点介绍了三种基于光学检测方法的分离式霍普金森技术，并简要说明了各个测量方法的特点。

关键词：光学检测；霍普金森压杆；动态特性；光干涉

中图分类号：TB301 文献标志码：A 文章编号：2095-2945（2018）09-0004-06

Abstract： The split Hopkinson pressure bar（SHPB） technology is an effective experimental method for measuring the dynamic mechanical properties of materials at high strain rates. The traditional Hopkinson pressure bar measurement method mainly uses strain gauges attached to the incident rod and transmission rod to achieve the purpose of measuring the dynamic mechanical properties of the material under test. However， there are still some inherent problems and shortcomings in this strain gauge Hopkinson pressure bar technology. In order to obtain more efficient and accurate experimental data， Hopkinson pressure bar measurement technology based on optical detection method came into being. It has the advantages of non-contact， high repeatability， more reliable and accurate measurement results. This paper traces the origin and development of the traditional split Hopkinson pressure bar technology， and the measuring device and the measuring principle are briefly reviewed. On this basis， three separate Hopkinson techniques based on optical detection are introduced， and the characteristics of each measurement method are briefly described.

Keywords： optical inspection （OI）； Hopkinson pressure bar （HPB）； dynamic characteristics； optical interference

1 概述

在军事和民用领域中的许多方面，类似于高速碰撞和爆炸等冲击加载形式的力学现象十分常见[1-2]。由于材料在高应变率加载下需要考虑结构惯性效应和材料应变率效应，因此材料在受到冲击荷载作用时所表现出的动态力学性能，与在静荷载作用下所表现出的静态力学性能存在着显著差异[3-4]。对于涉及冲击加载的工程项目来说，了解材料的动态力学性能是整个工程设计的基础，因此研究材料在冲击加载条件下的动态力学响应对于材料的工程设计和应用来说都具有很重要的現实意义。

研究材料动态力学性能的系列实验按应变率大小可分为中应变率实验（10～1021/s）、高应变率实验（102～1041/s）和超高应变率实验（104～1061/s）三种。针对材料不同应变率范围下的动态力学性能，常用的实验方法主要有电子伺服试验机、落锤实验机、分离式霍普金森杆和轻气炮[5-6]等。由于工程材料敏感性变化比较剧烈的范围[7]是102～1041/s，这个应变率范围正是分离式霍普金森杆实验方法所涉及的，加之其测量方法精巧、结构简单、易于操作和易于控制加载波形等[8]优点，分离式霍普金森杆实验技术已经成为研究中高应变率下材料动态力学性能的最主要和最可靠的实验技术。

分离式霍普金森压杆技术起源于1914年B.Hopkinson所设计的一套Hopkinson压杆实验装置[9]。在这套装置中，通过把测量冲量的长杆分为长短不一的两部分，实现了对冲击载荷随时间变化的实际波形的测量。到了1948年，Davies[10]将平行板电容器和圆柱形电容器引入到了Hopkinson压杆实验装置，实现了对压杆的轴向、径向两个方向位移的测量，使得霍普金森压杆技术取得了关键性的进展并得到了更多的关注。1949年，Kolsky[11]在原有装置的基础上通过将飞片加长的方式成功对Hopkinson压杆实验装置进行了分离，形成了分离式霍普金森压杆，也称为Kolsky压杆。这时的分离式霍普金森压杆中所使用的仍然是电容位移传感器。电容位移传感器首先得到的是位移信号，然后通过对位移的微分得到质点的速度信号，进而得到试样的应变信号。到1963年，Lindholm[12]把以往Kolsky压杆中的电容式传感器用粘贴于两杆上的电阻应变片取代，与电容位移传感器相比，电阻位移传感器可以直接测得杆表面的应变信息，至此才形成了现在的分离式霍普金森压杆（Split Hopkinson Pressuer Bar，简称SHPB，又名Kolsky杆）。随着数字化技术、计算机技术和测量仪器的发展，SHPB测量技术也在不断的提高。1976年，Tanaka[13-14]把数字化技术应用到了SHPB中，用于存储和分析应力波。1980年，Signoret[15]将微型计算机又引入到了SHPB装置中。80年代后，半导体应变片、压电晶体片、PVDF、高速摄影技术和光学测量技术相继用于分离式霍普金森压杆实验技术中[16]。目前分离式霍普金森压杆技术被广泛应用于金属[17]、陶瓷[18]、岩石[19]、混凝土[20]、橡胶[21]、生物组织[22]、记忆合金[23]、复合材料[24]、泡沫材料[25]等材料在高应变率下的动态力学性能的研究。

传统的SHPB测量方法主要是利用粘贴在入射杆和透射杆上的应变片实现对被测材料动态力学性能测量的目的，这些形似薄片的应变片需要用直流电源驱动，同时还需要用单臂电桥对所测信号进行放大[26]。实验过程中所测应变值取决于对测量信号的校准和电桥的放大。在这种测量中，需要应变片和测量表面间有很好的粘附性，否则会在很大程度上影响实验的结果，同时这种接触式的测量方式所能提供的测量精度有限。另外，由于当杆的直径小于3毫米时应变片和杆无法可靠连接，使得传统应变片式的分离式霍普金森压杆测量方法无法匹配亚微米级的试样，导致无法满足机械和国防等领域中对微小尺寸材料在高应变率下动态力学性能的测量需求。

针对传统应变片式的SHPB中所存在的种种不足和限制，已经有诸多学者提出过替代其中应变片式测量的方法。本文首先介绍传统SHPB的装置和原理，然后重点介绍三种基于光学检测方法的SHPB技术，并简要说明了各个测量方法的特点。

2 基本原理

分离式霍普金森压杆实验技术是以一维应力波理论为基础的，而一维应力波理论又建立在连续介质力学的基础之上[27-28]。连续介质力学的出发点不是从微观上去考虑物体真实的物质结构，而是把物质看作是一系列质点的连续集合。在连续介质力学中，可以采用物质坐标法或是空间坐标法来描述介质的运动。物质坐标法又称为拉格朗日方法，它是一种随着介质中某个固定的质点来观察物质运动的方法，这种方法所研究的是在给定的质点上物理量随着时间的变化，以及这些物理量从一个质点传递到其他质点时的变化。空间坐标法又称为欧拉方法，这种方法是在固定的某一空间点来观察物质的运动，它所研究的是在所设定的空间位置上以不同时刻到达该空间位置的不同质点的各个物理量随时间的变化，以及这些物理量从一个空间点传递到其他空间点时的变化。相对于描述连续介质运动的两种坐标系，在力学问题中也存在着两种处理方法[29-31]，即研究物质团的L氏法和研究空间场的E氏法。在固体力学中因为固体材料变形小和测点都固定在质点，所以常采用L氏法。而在流体力学中由于流体介质易流动和测点都固定在空间场，因此常采用E氏法。在典型的分离式霍普金森压杆实验中，基本是在物质坐标系下采用L氏法研究被测材料试样的动态响应情况。

典型的SHPB 实验测量装置包括动力系统、弹性压杆系统和应力波的数据采集与处理系统三个部分，如图1所示[32-33]。其中，动力系统包括气枪、榔头等类的驱动工具和打击杆，用以给整个装置提供初始的动力；弹性压杆系统包括入射杆、透射杆、加在两杆中间的被测材料试样和用以限制透射杆运动范围的阻尼器；应力波数据的采集和处理系统包括两个分别粘贴在入射杆和透射杆上的电阻应变片、对应变信号进行放大的前置放大器、示波记录仪和后续的数据处理系统。

传统的SHPB实验装置的工作过程如下[34]：首先将所要测量的材料试样夹持在入射杆和透射杆之间，用气枪或榔头等工具敲击打击杆，使其以一定的速度撞击入射杆，入射杆上产生压应力脉冲并沿着弹性压杆系统向被测材料试件方向传播。到达被测材料试样的压应力脉冲一分为二，一部分对试样加载并传向透射杆产生透射脉冲，另一部分被反射回入射杆形成反射脉冲。粘贴在入射杆和透射杆上的应变片分别记录下入射脉冲、反射脉冲和透射脉冲，通过一维应力波理论便可以确定杆上的应力、应变、应变率等随时间变化的情况。

这里需要指出的是，SHPB实验是建立在“杆中一维应力波假定”和“短试样应力/应变沿其长度均匀分布假定”之上的[35-36]。杆中一维应力波假定是说，当杆受到应力的作用产生形变时其横截面依旧保持为平面，沿其截面只有均布的轴向应力。短试样应力/应变沿其长度均匀分布假定是指材料在某一应变率范围受到冲击载荷的作用后具有唯一的应力-应变关系，即应力只是应变的单值函数。

并且，在霍普金森压杆的弹性区内，应变、应力和质点速度三者之间存在线性比例关系[39]：

3 基于光学检测方法的SHPB技术

3.1 基于光纤多普勒测速仪的SHPB技术

2004年，Strand等人提出了由光纤器件构成的光子多普勒测速法（Photonic Doppler Velocimetry，PDV），这种测速方法因其具有结构简单、非接触性、测量准确、操作简单、稳定可靠等优势[42-43]，在很多领域中得到了广泛应用，现已成为主要的测速技术。用PDV测量表面速度的原理如图2所示。光通过光纤探头照射到被测目标上，被测目标表面反射的光就是多普勒频移，它们其中的一部分被光纤探头收集。这些光和反射光在PDV系统中重新汇合。由于多普勒频移很小，现有设备无法直接对其进行测量，因此多是测量两者之间的拍频差，通过测量得到的拍频差即可得到被测目标表面的速度。

Casem等人将 PDV测速技术应用到了霍普金森压杆实验技术中[45]。应用PDV测量霍普金森压杆中粒子速度的方法有两种，如图3所示。PDV既可以如探頭1所示用于测量杆自由端的正交速度，也可以如探头2所示用于测量杆的横向速度。通常情况下是用如2所示的PDV装置取代霍普金森压杆中的应变片。PDV被安装在与杆成？兹的位置上，杆表面反射回探头的光取决于安装的角度？兹和杆表面的性质。将两套这样的PDV装置分别安装在入射杆和透射杆上就可以测量相应杆沿着角度？兹方向的速度。这种方法中用测量速度取代测量应变，所需的工程应变、应力和应变率可以通过Kolsky三波法公式（即：公式10～12）得出。

C.Avinadav等人对传统的PDV系统进行了改进，实现了全光纤的干涉速度仪，如图4所示[46]。与传统PDV系统不同的是，这里安装的PDV所要测量的是在几米每秒范围内快速变化的低速，这是很难用单相位测量方法实现。因此，他们的系统中包含了一个3×3的单模光纤耦合器以产生三个相互间有120°相位差的干涉信号。

基于全光纤干涉测速法的霍普金森压杆装置如图5所示。在这套装置中用干涉仪取代了应变片。两个光纤激光各自与杆成30°，分别照射在入射杆和透射杆上用以测量杆的速度。第三个光学测量是一个可选择进行的对试件本身的测量，光纤激光以90°的角度去测量试件的径向膨胀率。最后把一个PVDF薄膜传感器连在入射杆上对数据采集程序进行触发。

基于光纤多普勒测速仪的SHPB技术，通过PDV测量质点速度的方法消除了传统SHPB实验装置对测试时间的限制。在不受抛射体长度、杆尾部装置的限制下，可直接收集测量数据。用PDV方法测量SHPB中粒子速度时会存在弯曲波。弯曲波会使得杆、试件和抛射体间准直性变差，甚至使衬套的公差不能满足要求。因此在基于PDV方法的分离式霍普金森压杆实验装置中，需要通过在相对位置安装两个PDV的方法去消除弯曲波对整个测量实验的影响。

3.2 基于TDI和NDI的SHPB技术

在基于TDI（Transverse Displacement Interferometer）和NDI（Normal Displacement Interferometer）的SHPB技术中，使用横向位移干涉仪去测量入射杆上的入射脉冲和反射脉冲，用正向位移干涉仪去测量透射杆上的透射脉冲[47-48]。

图6是用TDI测量入射杆中与入射脉冲和反射脉冲相关的轴向位移的原理。在杆的中间位置有一个线距为P的衍射光栅，一束准直的单色光通过空间滤波器扩束滤波后形成入射光。入射光通过一个焦距为f的透镜后被聚焦到光栅上。光栅被定向安装，使其刻线垂直于轴和入射光。当杆移动时，光栅穿过聚焦光束，将会在每条支路上产生一个相位频移并对探测器造成干扰。所产生的条纹数n与光栅的运动ug有关，即：

这里p是光栅的周期数，k为光束衍射的级数，这里k=1。由于波是分开的，所以根据入射脉冲和反射脉冲可以确定入射杆上的轴向位移，通过对位移微分可以得到相应的速度信息。

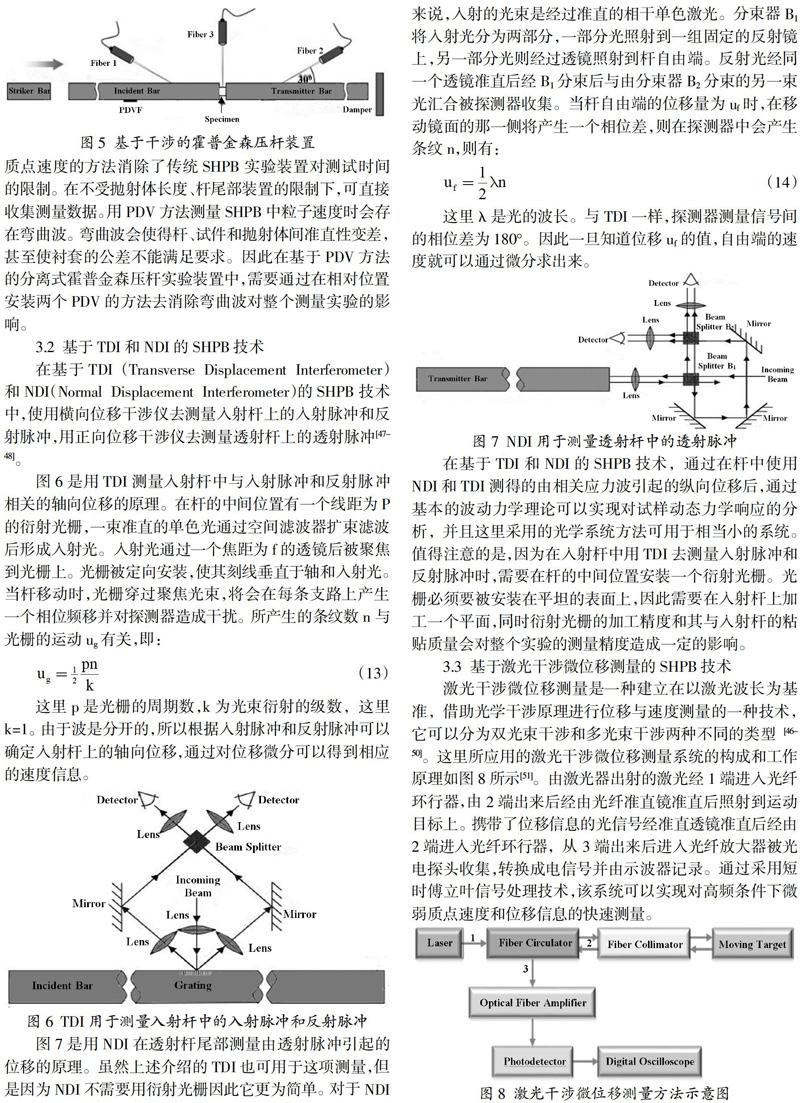
图7是用NDI在透射杆尾部测量由透射脉冲引起的位移的原理。虽然上述介绍的TDI也可用于这项测量，但是因为NDI不需要用衍射光栅因此它更为简单。对于NDI来说，入射的光束是经过准直的相干单色激光。分束器B1将入射光分为两部分，一部分光照射到一组固定的反射镜上，另一部分光则经过透镜照射到杆自由端。反射光经同一个透镜准直后经B1分束后与由分束器B2分束的另一束光汇合被探测器收集。当杆自由端的位移量为uf时，在移动镜面的那一侧将产生一个相位差，则在探测器中会产生条纹n，则有：

这里？姿是光的波长。与TDI一样，探测器测量信号间的相位差为180°。因此一旦知道位移uf的值，自由端的速度就可以通过微分求出来。

在基于TDI和NDI的SHPB技术，通过在杆中使用NDI和TDI测得的由相关应力波引起的纵向位移后，通过基本的波动力学理论可以实现对试样动态力学响应的分析，并且这里采用的光学系统方法可用于相当小的系统。值得注意的是，因为在入射杆中用TDI去测量入射脉冲和反射脉冲时，需要在杆的中间位置安装一个衍射光栅。光栅必须要被安装在平坦的表面上，因此需要在入射杆上加工一个平面，同时衍射光栅的加工精度和其与入射杆的粘贴质量会对整个实验的测量精度造成一定的影响。

3.3 基于激光干涉微位移测量的SHPB技术

激光干涉微位移测量是一种建立在以激光波长为基准，借助光学干涉原理进行位移与速度测量的一种技术，它可以分为双光束干涉和多光束干涉两种不同的类型[46-50]。这里所应用的激光干涉微位移测量系统的构成和工作原理如图8所示[51]。由激光器出射的激光经1端进入光纤环行器，由2端出来后经由光纤准直镜准直后照射到运动目标上。携带了位移信息的光信号经准直透镜准直后经由2端进入光纤环行器，从3端出来后进入光纤放大器被光电探头收集，转换成电信号并由示波器记录。通过采用短时傅立叶信号处理技术，该系统可以实现对高频条件下微弱质点速度和位移信息的快速测量。

基于激光干涉微位移测量的SHPB技术的原理如图9所示。实验前将两个与杆的材质和直径相同的激光反射片用高强度胶粘贴在入射杆和透射杆的端面。激光反射片的厚度为1mm，耳片尺寸R与光纤探头的尺寸相当。实验时，被测材料试样被安装在两个反射耳片间，并把激光干涉微位移测量系统中的光纤探头对准反射片上的耳片中心。当试样的左右两个端面分别受到入射脉冲和透射脉冲的作用后，所产生的端面速度v1和v2由光纤探头通过反射耳片实时测量得到。

被测材料的动态力学性能可由下式求得：

基于激光干涉微位移测量的SHPB技术，通过测量两杆端面速度的方式实现了对材料试样应力-应变关系的直接测量。这种方法使得在杆中传播的应力波可以被忽略，因此在长脉冲加载、粘弹性杆以及温实验中具有一定优势。但是，在进行基于激光干涉微位移测量的SHPB实验前需要提前设计相应的激光反射片，并用高强度胶将其固定在两杆的端面。

4 结束语

本文主要介绍了取代传统的分离式霍普金森压杆技术的三种用光学检测装置。总的来说，这些基于光學检测方法的SHPB技术与传统的应变片式测量方法相比，具有非接触性、高度可重复性、测量结果更加可靠和准确等优点。同时，光学方法的主要优点是它对于应变计无法测量的微型棒可以进行测量。尽管基于光电检测方法的SHPB技术中还存在着一些有待提升的地方，但是为了满足更高应变率和更小尺寸材料试的测试需求，以及为了获得更高效、精确的实验数据，基于光电检测方法的SHPB技术是今后研究的主要方向。

参考文献：

[1]占国平.基于分离式霍普金森压杆实验技术的脆性材料动态性能研究[D].武汉：武汉纺织大学，2013：1-5.

[2]钱凯君.石英晶体传感器在软材料霍普金森压杆实验中的应用研究[D].浙江：浙江大学，2015：1-4.

[3]Field J E， Walley S M， Proud W G， et al. Review of experimental techniques for high rate deformation and shock studies[J]. International Journal of Impact Engineering， 2004，30（7）：725-775.

[4]谢林茂.摆锤冲击加载岩石动态试验装置的研制[D].沈阳：东北大学，2011：1-2.

[5]Gama， Lopatnikov， Gillespie Jr. Hopkinson bar experimental technique： A critical review[J]. Applied Mechanics Reviews， 2004，57（4）：223-250.

[6]禹琦.高温下素混凝土SHPB抗冲击性能试验研究[D].长沙：湖南大学，2011：1-6.

[7]臧小为.霍普金森压杆过载波形整形及系统分析软件研究[D].南京：南京理工大学，2010：1-6.

[8]郑文，徐松林，蔡超，等.基于Hopkinson压杆的动态压剪复合加载实验研究[J].力学学报，2012，44（01）：124-131.

[9]Hopkinson B. A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets[J]. Philosophical Transactions of the Royal Society of London， 1914：213（612）：437-456.

[10]Davies E D H， Hunter S C. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar[J]. Journal of the Mechanics & Physics of Solids， 1963，11（3）：155-179.

[11]Kolsky H. An investigation of the mechanical properties of materials at very high rates of loading[J]. Proceeding Journal of American Physical Society， 1949，B62：676-700.

[12]Lindholm U S. Some expeirments with the split Hopkinson pressure bar[J]. Journal of the Mechanics and Physics of Solids， 1964：317-335.

[13]Tanaka K， Ogawa K. Deformation of pure titanium and titaniun alloys at high strain rate[C]. Proceedings of 19th Japan Congress on Materials Research， 1976：43-47.

[14]Tanaka K， Ogawa K. The static and dynamic compressive strength of titanium and Ti-alloys[C]. Proceedings of 2nd International Congress on the Materials Behavior of Materials，1976：1598-1602.

[15]Signoret C， Pouyet J M， Lataillade J L. Adaptation of a microcomputer system to a modified split Hopkinson bar[J]. Journal of Physics E Scientific Instruments， 1980，13（12）：1284-1286.

[16]姜錫权，胡时胜.霍普金森杆实验技术发展综述[A].Hopkinson杆实验技术研讨会会议论文集[C].2007：156-167.

[17]Gray G T， Blumenthal W R. Split-Hopkinson pressure bar testing of soft materials[J]. Asm Handbook， 2000，8：462-476.

[18]Blumenthal W R， Gray G T I， Blumenthal W R. Characterizations of shock-loaded aluminum-infiltrated boron carbide cermets[J]. Shock Compression of Condensed Matter， 1989：393-396.

[19]刘剑飞，胡时胜，胡元育，等.花岗岩的动态压缩实验和力学性能研究[J].岩石力学与工程学报，2000，19（5）：618-621.

[20]胡时胜，王道荣，刘剑飞.混凝土材料动态力学性能的实验研究[J].工程力学，2001，18（5）：115-118.

[21]Li Q M， Meng H. About the dynamic strength enhancement of concrete-like materils in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures， 2003，40（2）：343-360.

[22]王宝珍，胡时胜.猪后腿肌肉的冲击压缩特性实验[J].爆炸与冲击，2010，30（1）：33-38.

[23]Bragov A M， Galieva A， Grigorieva V， et al. Functional properties of TiNi shape memory alloy after high strain rate loading[J]. Materials Science Forum， 2013，739：326-331.

[24]Tay T E， Ang H G， Shim V P W. An empirical strain rate-dependent constitutive relationship for glass-fibre reinforced epoxy and pure epoxy[J]. Composite Structures， 1995，33（4）：201-210.

[25]Rinde J A， Hoge K G. Time and temperature dependence of the mechanical properties of polystyrene bead foam[J]. Journal of Applied Polymer Science， 1971，15（6）：1377-1395.

[26]Casem D T， Fourney W L， Chang P. A polymeric split Hopkinson pressure bar instrumented with velocity gages[J]. Experimental Mechanics， 2003，43（4）：420-427.

[27]杜庆华，郑百哲.应用连续介质力学[M].北京：清华大学出版社，1984：5-8.

[28]王立礼.应力波基础[M].北京：国防工业出版，2005：1-9.

[29]乔丕忠，张勇，张恒，等.近场动力学研究进展[J].力学季刊，2017，38（01）：1-13.

[30]冯晓九，梁立孚.Lagrange方程应用于连续介质力学[J].北京大学学报（自然科学版），2016，52（04）：597-607.

[31]董钢.分离式霍普金森压杆实验技术数值模拟[D].安徽：合肥工业大学，2005：6-8.

[32]赵习金.分离式霍普金森压杆实验技术的改进和应用[D].中国人民解放军国防科学技术大学，2003：2-6.

[33]宋博.霍普金森压杆实验中的脉冲整形技术[A].第三届全国爆炸力学实验技术交流会论文集[C].2004：70.

[34]李玉龙，郭伟国，徐绯，等.Hopkinson压杆技术的推广应用[J].爆炸与冲击，2006，05：385-394.

[35]刘卫，孙晓霞，沈瑞琪，等.霍普金森压杆实验中试件过载的模型分析[J].兵工学报，2014，35（S2）：100-105.

[36]李为民，许金余.大直径分离式霍普金森压杆试验中的波形整形技术研究[J].兵工学报，2009，30（03）：350-355.

[37]胡时胜.霍普金森压杆技术[J].兵器材料科学与工程，1991（11）：40-47.

[38]李少华.霍普金森压杆试验中的两种波形整形技术研究[D].沈阳：东北大学，2014：7-16.

[39]吕雪莹.猪膝关节软骨的动态力学性能测试[D].浙江：浙江大学，2014：12-16.

[40]Ravichandran G， Subhash G. A micromechanical model for high strain rate behavior of ceramics[J]. International Journal of Solids & Structures， 1995，32（17-18）：2627-2646.

[41]傅华，彭金华，李俊玲，等.一种适合于Hopkinson杆的实验测试方法探索[J].高压物理学报，2014，28（4）：423-428.

[42]袁樹云，刘寿先，王德田，等.光纤多普勒测速仪位移模式数据处理新方法[J].激光与光电子学进展，2014，51（03）：72-76.

[43]李建中，刘寿先，刘俊，等.基于单探头实现两种技术同步复测的新测速仪[J].中国激光，2015，42（10）：173-179.

[44]李建中，刘寿先，刘俊，等.光子多普勒测速仪的单探头多目标测速能力研究[J].中国激光，2014，41（11）：132-136.

[45]Casem D T， Zellner M B. Kolsky bar wave separation using a photon doppler velocimeter[J]. Experimental Mechanics， 2013，53（8）：1467-1473.

[46]Avinadav C， Ashuach Y， Kreif R. Interferometry-based Kolsky bar apparatus.[J]. The Review of scientific instruments， 2011，82（7）：073908.

[47]张磊，李英雷，王悟.压剪炮的激光测速的系统[J].实验力学，2005，20（3）：434-440.

[48]Casem D T， Grunschel S E， Schuster B E. Normal and transverse displacement interferometers applied to small diameter kolsky bars[J]. Experimental Mechanics， 2012，52（2）：173-184.

[49]王东平，吴志会，倪明阳，等.光纤激光精密位移调整技术实验研究[J].激光与光电子学进展，2014，51（9）：122-127.

[50]段小艳，任冬梅.激光干涉法微位移测量技术综述[J].计测技术，2012，32（6）：1-5.

[51]唐孝容，谭多望，汪斌，等.激光干涉仪在微型爆炸容器研究中的应用[J].应用激光，2008（05）：383-385+398.

[52]Fu H， Tang X R， Li J L， et al. An experimental technique of split Hopkinson pressure bar using fiber micro-displacement interferometer system for any reflector[J]. Review of Scientific Instruments， 2014，85（4）：045120-045120-5.