因子分析-概率神经网络模型在边坡稳定性评价中的应用

王佳信，周宗红，付 斌，李克钢，王海泉

(1.昆明理工大学国土资源工程学院，云南 昆明 650093；2.中南大学资源与安全工程学院，湖南 长沙 410083)

随着大规模岩土工程的开展，在矿山、水利、交通以及环境等工程中人工开挖或者天然边坡稳定性问题越来越突出。边坡一旦发生崩塌、滑坡等失稳破坏，将会造成巨大的经济损失，因此，边坡的稳定性评价直接关系到工程建设资金投入、人民生命财产安全以及相应防治措施采取，边坡稳定性的分析、评价及其发展趋势的预报具有重要的工程实际意义[1～2]。

近年来，许多新方法诸如微震监测[3]、云模型[4]、人工免疫算法[5]、SVM模型[6]以及BDA模型[7]等不断呈现，使得边坡稳定性评价更科学，且都取得了一定的成果，但仍存在一定的缺陷。例如文[5]中变异概率pm和交叉概率pc对算法影响较大，pm和pc参数值确定后，算法易过早收敛和陷入局部最优。以上部分综合评价模型中，专家们往往尽可能地收集更多边坡稳定性评价指标，但过多评价指标很难在处理问题中发挥优势，甚至成为解决问题的绊脚石，基于此，应寻求多种方法结合辨识边坡稳定性问题。

本文提出一种因子分析和概率神经网络结合边坡稳定性评价模型，PNN是在RBFNN的基础上融合Bayes 决策理论以及密度函数估计，但是PNN径向基函数还保留RBFNN中常采用的高斯函数。鉴于此，文[8]采用Alpha稳定分布改进PNN样本层中径向基函数；文[9]采用遗传算法优化样本层节点数目以及平滑参数δ，以上的改进都取得了一定的成果。本文借签一种多元统计方法——因子分析，对边坡稳定性评价指标数据进行压缩和特征信息提取，因子分析后的指标数据满足PNN模型中径向基函数采用高斯函数的要求。此外，因子分析在边坡工程领域内的应用主要体现在指标权重的确定上[10]，对边坡稳定性评价至今还鲜见文献报道。本文采用因子分析对指标数据降维同时采用综合函数对边坡稳定性进行评价。在因子分析的基础上，建立边坡稳定性评价PNN模型，并以39个典型边坡实例验证模型的有效性。

1 因子分析-概率神经网络模型

1.1 因子分析模型[10]

设p维总体X=(X1,X2,…,Xp)T的均值为μ=(μ1,μ2,…,μP)T，协方差矩阵Σ=(σij)p×p，相关系数矩阵R=(ρij)p×p，因子分析模型为：

(1)

式中：F1,F2,…,Fm——m个公因子；

εi——变量Xi独有的特殊因子(i=1, 2,…,p)；

aij——变量Xi在公因子Fi上的载荷(i=1, 2,…,p；j=1, 2,…,m)。

为了消除逆向指标对综合评价的影响以及指标量纲对PNN模型的影响，在进行因子分析前需对指标进行正向化和标准化，其表达式分别如下：

(2)

(3)

式中：Yij——指标正向化后的值；

xij——第i项指标第j个样本原始数据；

Si——第i项指标第j个样本标准差；

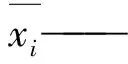
以上变量中，i=1, 2,…,p；j=1, 2,…,m。

1.2 概率神经网络模型

概率神经网络[8～9](PNN)是一种基于径向基函数和经典的概率密度估计原理建立的神经网络，其网络结构见图1。PNN的算法步骤如下：

图1 概率神经网络结构Fig.1 Structure of the probabilistic neural network

首先，将待测样本向量X输入输入层，其中神经元数目与样本维数相等。样本层(部分学者称为模式层)计算待测样本向量X与训练样本间的距离，该层每个节点单元的输出计算为：

f(X,Wi)=exp[-(X-Wi)T(X-Wi)/2δ2]

(4)

式中：Wi——输入层到样本层的权重；

δ——平滑参数。

然后，求和层进行某类的概率密度函数(probability density function, PDF)求和，由Parzen方法可得各类PDF估计：

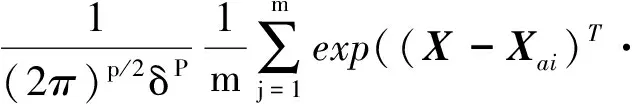
(X-Xai)/2δ2)

(5)

式中：Xai——i个训练样本向量；

m——训练样本个数。

最后，竞争层输出各类概率密度函数，概率最大值的那一类为1，其他类别为0。

2 因子分析-概率神经网络模型

2.1 因子分析的PNN模型预测步骤

因子分析-概率神经网络模型边坡稳定性评价技术路线见图 2，主要步骤如下：①首先采用因子分析对指标数据进行降维处理；②将因子分析后的因子得分数据作为PNN输入层，建立边坡稳定性评价的PNN模型；③设置SPREAD值，对网络进行训练和测试；④得出边坡稳定性评价结果。

2.2 建立边坡稳定性评价指标体系

影响边坡稳定性主要因素有岩土体结构特征和物理力学性质，本文根据《建筑边坡工程技术规范》(GB 50330—2013)[11]及罗战友和史秀志等[7～8]的研究成果，选取岩体重度(X1)、黏聚力(X2)、内摩擦角(X3)、边坡角(X4)、边坡高度(X5)以及孔隙水压力比(X6) 作为边坡稳定性评价指标，将边坡分为稳定S(Stable)和失稳F(Failure) 2个类别，以文[7]中39组边坡实测数据(表1)作为学习样本。

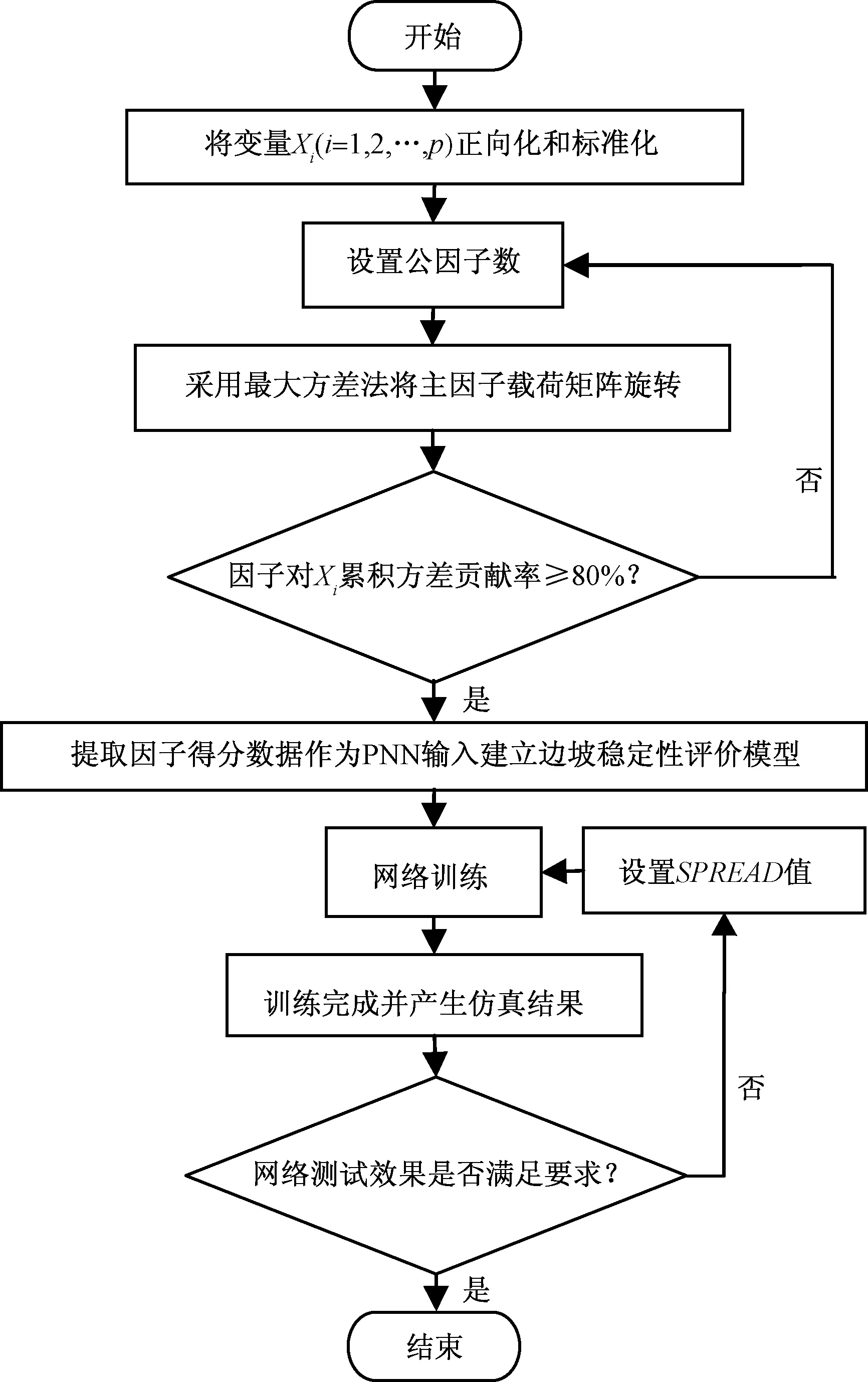
图2 因子分析的PNN边坡稳定性评价模型技术路线Fig.2 Technology roadmap of the slope stability evaluation model of PNN based on factor analysis

2.3 因子分析结果

首先对表1中39个样本6个指标数据进行正向化，然后采用SPSS软件(指标数据标准化自动执行)进行因子分析。一般情况下，优先考虑较多的公因子，然后根据结果再减少因子数，但此过程过于繁琐。Mardia给出不同公共主因子数，所应具备最少原始变量数之间关系(表2)，本文先将主因子个数定为3进行因子分析。

因子分析的总方差解释见表3，针对主因子数目确定，常用累积方差贡献率80%来确定主因子数目[12]。Kaiser主张将特征值小于1的主因子舍去；由表3可以看出，经最大方差法旋转后，前3个因子变量的特征值均大于1，前3个主因子累积方差贡献率为 83.830%，包含原有信息83.830%，提取前3个主因子较为合适。

非金属夹杂物级别虽然不高，但在样品中心V形裂纹附近出现了硫化物类夹杂物（1级），非金属夹杂物的存在破坏了钢基体的连续性，严重影响钢的力学性能，产生应力集中，拉拔时不能与基体同步变形，在非金属夹杂物与基体结合部位引起应力集中，导致裂纹在此处萌生及扩展，最终导致盘条拉拔断裂。

主因子载荷表征主因子与原始变量间相关系数，主因子载荷矩阵旋转之后载荷(表4)系数更接近1或者0，这样主因子能够更好地解释和命名变量。由表 4可以看出，第一主因子F1与指标X2、X3和X4显著相关，F1综合黏聚力、内摩擦角和边坡角等指标信息。第二主因子F2与指标X1和X5显著相关，F2综合岩体重度和边坡高度指标信息，且X1在F2上为正值，F2可称为岩体重度因子。第三主因子F3仅与X6变量显著相关性，F3可称为孔隙水压力比因子；F1、F2与F3包含6个指标大部分信息(83.830%)。

表1 边坡稳定性的PNN模型评价结果Table 1 Evaluation results of slope stability of the PNN model

注：“*”代表测试样本

表2 主因子数与原始变量数关系Table 2 Relationship between the number of principal factors and the number of original variables

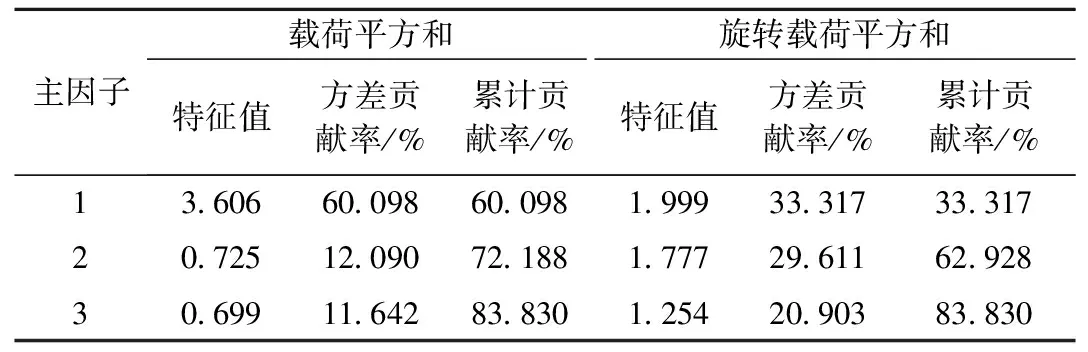
表3 总方差解释Table 3 Total variance interpretation

表4 旋转后因子载荷矩阵Table 4 Factor loading matrix after rotation

表5 因子得分系数矩阵Table 5 Coefficient matrix of factor scores

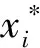
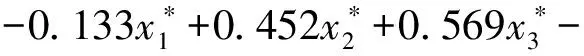
(6)

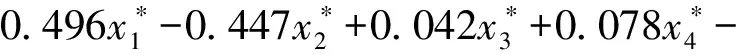
(7)

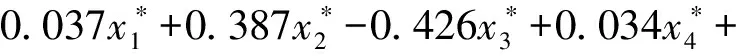
(8)

首先将表1中样本数据正向化、标准化，然后将处理后数据代入式(6)～(8)进行主因子得分数据的计算，结果见表 6。F1与F2之间各主因子之间得分散点图见图3。F1与F2分别包含原来信息量的33.317%和29.611%；主因子得分图能够反映对象与指标之间关系。由图3可以看出，在第一象限(正向区间)内，F1与F2值越大，从总体上来说，岩体重度、黏聚力和内摩擦角取值就越大，正向区间内的12个样本(12、14～16、22～25、32、36和38～39)的边坡就越容易向破坏趋势发展。限于篇幅，图3中其他象限将不再具体分析，F1与F3以及F2与F3得分散点图不列出。

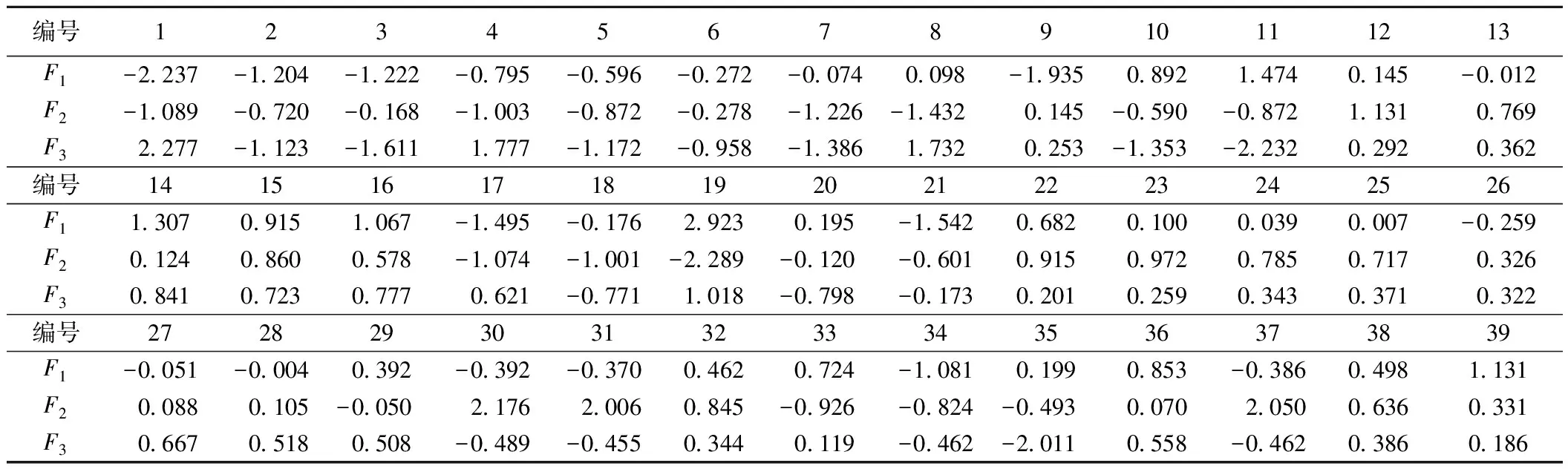
表6 主因子得分数据Table 6 Principal factor scores

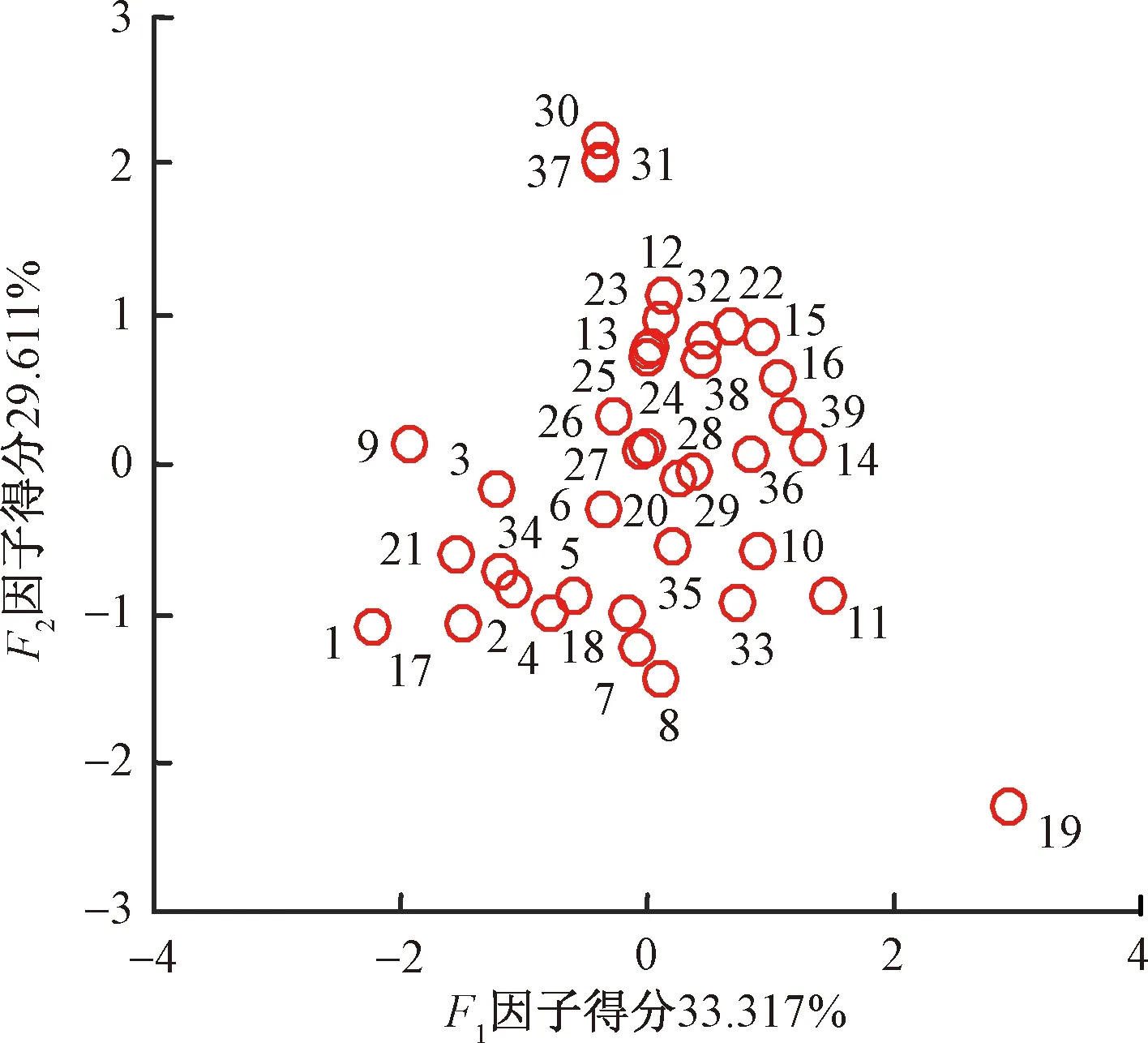
图3 主因子 F1和F2 得分散点图Fig.3 Scatter plot of principal factor scores of F1 and F2

采用综合评价函数对39组样本边坡稳定性进行定量分析，采用综合评价函数：

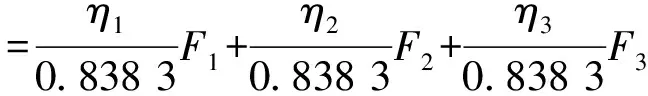
(9)

式中：η1、η2和η3——公因子F1、F2和F3各自方差贡献率；

0.838 3——累积方差贡献率。

将式(6)～(8)代入式(9)得到：

(10)

由式(3)和式(10)可以计算得到综合主因子得分数据(表7)；将综合主因子得分结果在d=(0.848+1.013)/2=0.930 5下可分为2种类型的边坡，因指标进行正向化处理，第一类边坡为失稳边坡：综合主因子得分范围为[-0.083, 0.848)，该区间包括8#、12#～16#、19#、22#～33#和36#～39#等23个样本；从表2可以看出，除8#、12#、13#、14#和33#等样本的边坡稳定性被划分到失稳外，其余样本的评价结果与实际情况一致。第二类边坡为稳定边坡，综合主因子得分取值范围为[-1.013，-0.083)，该区间包括1#～7#、9#～11#、17#～18#、20#～21#和34#～35#等16个样本；从表2可以看出，除17#、18#、20#和21#号样本的失稳边坡被划分到稳定外，其余样本评价结果与实际一致。

2.4 PNN模型仿真结果

采用3个主因子得分数据(表6)进行概率神经网络仿真，为了简明地评价边坡稳定性情况，将PNN模型期望输出值设置为1(F)和2(S)，其中，F和S代表边坡失稳和稳定2种类型。此外，为检验PNN模型泛化能力，将表6中39个样本构造5种学习情况，即将训练样本与测试样本个数比分别设为34∶5、32∶7、30∶9、28∶11和26∶13，以探讨训练样本个数对PNN模型精度影响。其中径向基函数分布密度SPREAD值设置为0.05。同时，将表1(未经因子分析)39个样本构造上述5种情况进行学习，限于篇幅，仅列出训练与测试样本个数比为32∶7的学习情况(图4～5)。

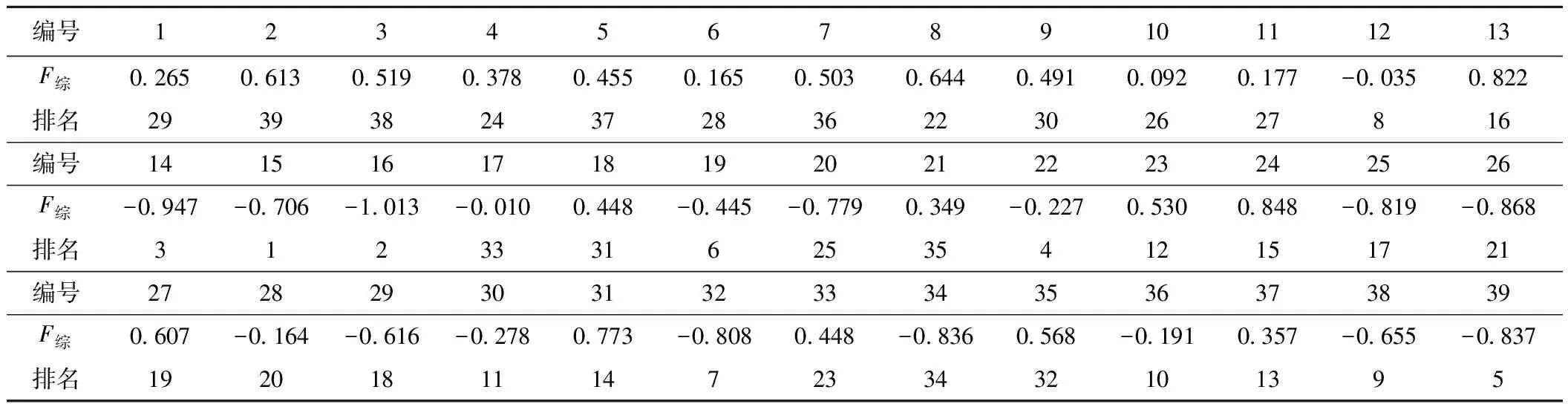
表7 综合主因子得分及其排名Table 7 Comprehensive principal factor scores and their rankings

图4 经因子分析边坡样本1#～32#训练效果和误差结果及33#～39#测试效果Fig.4 Training effects and the error results of slope samples 1#～32# and test results of 33#～39# by factor analysis

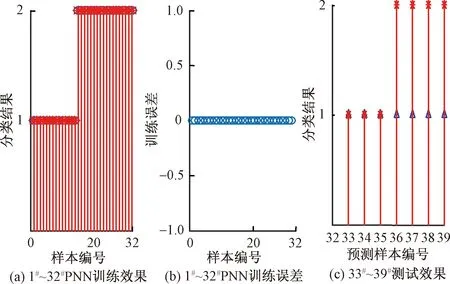
图5 未经因子分析边坡样本1#～32#训练效果和误差结果及33#～39#测试效果Fig.5 Training effects and the error results of slope samples 1#～32# and test results of 33#～39# without factor analysis

由图4可以计算出，指标数据经因子分析降维处理后，PNN模型的正判率为94.87%。同理，由图5可以计算出，未经因子分析降维处理的指标数据，PNN模型正判率为89.74%。经因子分析后的PNN模型预测精度提高了5.72%。为便于比较，表1中同时列出人工免疫算法[5]、SVM模型[6]以及BDA模型[7]的判别结果。由表1可以看出，除33和34号样本判别存在一定的偏差外，PNN模型评价结果与人工免疫算法、SVM模型以及BDA模型的判别结果基本一致。

5种不同训练和测试样本个数下PNN模型仿真统计结果见图6和表8。由图6可以看出，随着训练样本个数减少，PNN模型预测精度越来越低。因子分析后的PNN模型比采用原始数据建立的PNN模型更优。

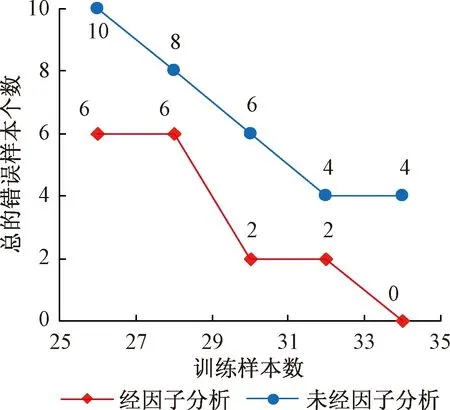
图6 训练样本数对PNN模型的影响Fig.6 Effect of training samples on PNN model

3 讨论

(1)39组样本数据是否适合采用因子分析？一般认为，相关系数的绝对值为0.8时为高度相关，可采用因子分析对指标数据进行降维处理。由表1计算得到指标X3与X4相关性最高，其相关系数为0.794，可采用因子分析方法，其实这种方法是欠妥的。样本数量不同，0.8的相关系数可信度也就不同；根据相关系数临界值rα[12]，对于2个变量4个样，相关系数为0.8时可信度只有90%。常采用KMO(Kaiser Meyer Olkin)统计量和BartlettP球形检验作为因子分析使用条件(表9)。由SPSS软件得到KMO 和Bartlett检验结果(表9)。由表可以看出，本文采用因子分析对表1中39个样本数据进行降维处理是可行的。

表8 因子分析前、后PNN模型的5种学习情况 (SPREAD=0.05)Table 8 Five learning situations of PNN model by Factor Analysis and without Factor Analysis (SPREAD=0.05)

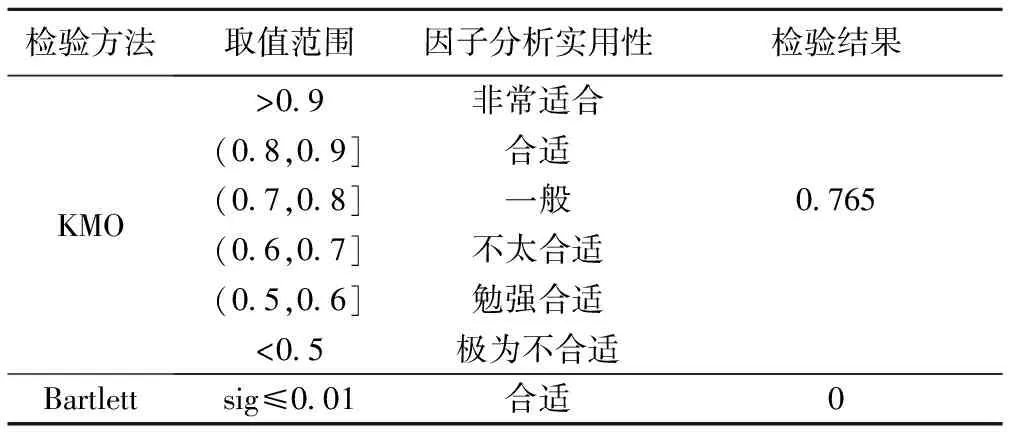
表9 KMO和Bartlett 的检验标准Table 9 Test standard of KMO and Bartlett

(2)SPREAD参数值影响着PNN模型的预测精度，SPREAD值越小，函数逼近越精确；SPREAD值越大，模型预测误差越大，其默认值为1。针对表8的评价结果，SPREAD值设置为0.05，使得PNN模型预测效果达到最优。以表6中39个样本为例，将1#～32#样本作训练，33#～39#样本作测试，SPREAD值设为0.1，检验PNN模型的可靠性(图7)可以看出，PNN模型正判率92.31%，可见PNN模型在边坡稳定性评价中是有效的。

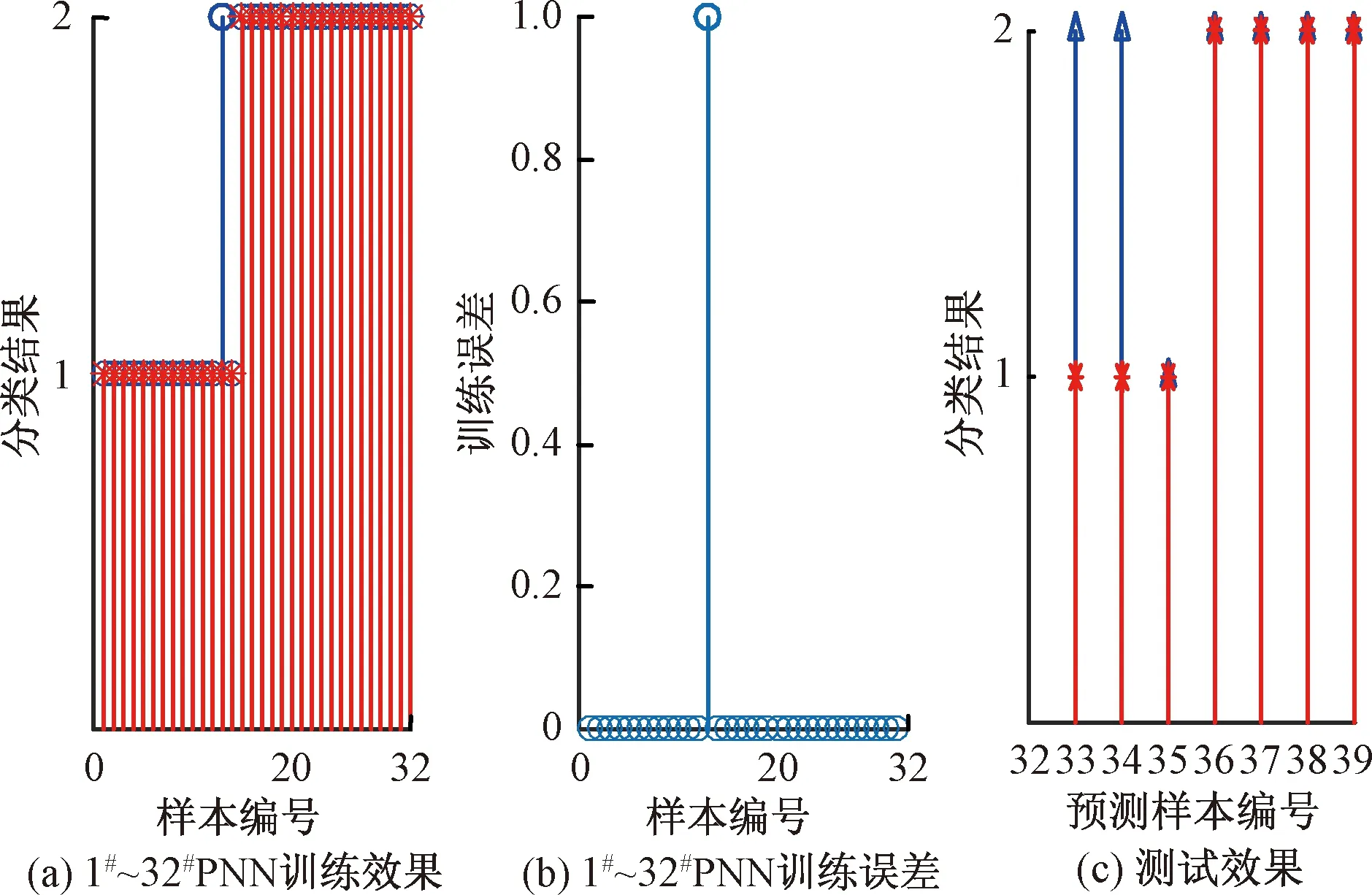
图7 SPREAD值为0.1下PNN模型训练和误差结果及测试效果Fig.9 Test results, training effects and the error results when the value of SPREAD is 0.1

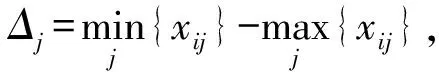
(11)

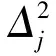
D(Zj)——原始数据相似变换后的方差。

i=1,2,3,…,p;j=1,2,3,…,m。

值得一提的是，边坡稳定性问题不仅受岩土体结构特征和物理力学性质的影响，还受暴雨、地震和人工活动等一系列因素影响，使得边坡稳定性评价成为一项艰难的课题，边坡稳定性评价还有待于进一步研究和探讨。

4 结论

(1)边坡稳定性评价模型——因子分析-概率神经网络模型，PNN模型总收敛于Bayes优化解，样本追加能力强，可容忍一些判别错误的样本，使边坡稳定性评价更加科学合理，为边坡稳定性评价提供一种很好的思路。

(2)采用因子分析提取边坡稳定性评价的3个新综合指标，尽可能多地保留原始变量的信息；提取的综合指标彼此独立，解决指标信息重叠、多重共线性以及PNN模型采用高斯函数等诸多问题，进一步提高了PNN模型预测精度。

(3)39个典型的边坡工程实例预测结果表明：指标数据经因子分析后，构造5种不同训练和测试样本数，PNN模型仍具有较好的评价效果，其正判率分别为100%、94.87%、94.87%、84.62%和84.62%，说明因子分析后的PNN模型在边坡稳定性判别中是有效的。

[1] Kumar M，Rana S，Pant P D，etal. Slope stability analysis of Balia Nala landslide，Kumaun Lesser Himalaya, Nainital, Uttarakhand，India[J]. Journal of Rock Mechanics & Geotechnical Engineering，2017， 9(1)：150-158.

[2] 向章波，张家铭，周晓宇，等. 基于Slide的某红层路堑边坡稳定性分析[J]. 水文地质工程地质，2015，42(4):90-95. [XIANG Z B，ZHANG J M，ZHOU X Y，etal. The slope stability analysis of red bed based on Slide [J]. Hydrogeology & Engineering Geology，2015，42(4):90-95. (in Chinese)]

[3] Salvoni M，Dight P M. Rock damage assessment in a large unstable slope from microseismic monitoring-MMG Century mine (Queensland，Australia) case study[J]. Engineering Geology，2016，210：45-56.

[4] 张军，陈征宙，刘登峰，等. 基于云模型的岩质边坡稳定性评估研究[J]. 水文地质工程地质，2014，41(6)：44-50.[ZHANG J，CHEN Z Z，LIU D F，etal.Stability evaluation of a rock slope based on the cloud model[J]. Hydrogeology & Engineering Geology，2014,41(6)：44-50.(in Chinese)]

[5] 张豪，罗亦泳. 基于人工免疫算法的边坡稳定性预测模型[J].煤炭学报，2012，37(6)：911-917.[ZHANG H，LUO Y Y. Prediction model for slope stability based on artificial immune algorithm[J]. Journal of China Coal Society，2012，37(6)：911-917. (in Chinese)]

[6] 罗战友，杨晓军，龚晓南，等.基于支持向量机的边坡稳定性预测模型[J]. 岩石力学与工程学报，2005，24(1)：144-148.[LUO Z Y，YANG X J，GONG X N，etal.Support vector machine model in slope stability evaluation[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(1)：144-148. (in Chinese)]

[7] 史秀志，周健，郑纬，等. 边坡稳定性预测的Bayes判别分析方法及应用[J]. 四川大学学报(工程科学版)，2010，42(3):63-68.[SHI X Z，ZHOU J，ZHENG W，etal.Bayes Discriminant Analysis method and its application for prediction of slope stability[J]. Journal of Sichuan University(Engineering Science Edition)，2010，42(3)：63-68. (in Chinese)]

[8] 王佳信，周宗红，赵婷，等. 基于 Alpha 稳定分布概率神经网络的围岩稳定性分类研究[J].岩土力学，2016，37(增刊2)：649-657.[WANG J X，ZHOU Z H，ZHAO T，etal. Application of Alpha stable distribution probabilistic neural network to classification of surrounding rock stability assessment[J]. Rock and Soil Mechanics，2016，37(Sup2)：649-657. (in Chinese)]

[9] 连远锋，李国和，吴发林，等.基于遗传PNN网络的组合导航故障诊断研究[J].仪器仪表学报，2012，33(1)：120-126.[LIAN Y F，LI G H，WU F L，etal. Fault-diagnosis method for INS/GPS integrated navigation system based on PNN and genetic algorithm[J]. Chinese Journal of Scientific Instrument，2012，33(1)：120-126. (in Chinese)]

[10] 赵建军，贺宇航，黄润秋，等. 基于因子分析法的边坡稳定性评价指标权重[J]. 西南交通大学学报，2015，50(2：):325-330.[ZHAO J J，HE Y H，HUANG R Q，etal. Weights of slope stability evaluation indexes based on factor analysis method[J]. Journal of Southwest Jiaotong University，2015，50(2):325-330. (in Chinese)]

[11] GB50330—2013 建筑边坡工程技术规范[S]北京：中国建筑工业出版社，2013.[GB50330—2013 Technical code for building slope engineering[S]. Beijing：China Construction Industry Press，2013. (in Chinese)]

[12] 杨虎，刘琼荪，钟波.数理统计[M].北京：高等教育出版社，2004:199-207.[YANG H，LIU Q S，ZHONG B. Mathematical statistics[M].Beijing: Higher Education Press，2004:199-207.(in Chinese)]