面曲率在自由曲面多轴加工中的应用

李立军 张 爽 曹 剑 白广华

1 背景介绍

多轴数控加工自由曲面时，通常使用球头铣刀进行半精加工和精加工，当铣削到凹曲面曲面变化较大的地方，铣削力会陡变，可能会发生振刀偏心等现象，导致加工质量下降。工程师在应对此情况时，通常采用变更刀轨策略，通过降低走刀速度、调整刀具加工姿态等降低切削力波动以保证加工质量。在曲面上包覆等参数网格，通过矢量运算得到刀位点所在曲面网格，通过CAD软件得到网点坐标。运用Voronoi元方法，能够通过刀位点所在曲面上的点云的坐标计算得到该曲面上任意位置的面曲率。对于凹曲面，曲面变化的程度可通过面曲率值有效量化，进而可使用该数值作为加工编程的参考依据。

在零件表面以网格形式取点云，网格完整包覆零件上所有点。曲面上的点表示为：S(x,y,z)。自由曲面一般由球头铣刀完成加工，通过偏置一个刀具半径就能得到刀位刀具半径，θt为前倾角，θn为侧倾角）。

在某区域A1内曲面某点的曲率可用ζi来表示，区域A1内的点集表示为P1。

2 曲面上点的高斯曲率的计算

通过Voronoi方法计算高斯曲率。在三角形网格上估算曲率。曲面上某一点xi的平均曲率可由下式得到：

k为领域内点个数。矩阵C最小特征向量λmin可近似看作曲面在该点的法向量。

在三角形网格上估算平均曲率。曲面上某一点xi的平均曲率可由下式得出[1]：

其中n是法向量，A是周围一个无限小的区域的面积，diam(A)是这个区域的直径，5表示梯度（对x,y,z求导）。Kp(xi)=2kHn记为平均曲率向量。

高斯曲率可由下公式得到[2]：

A是xi所在Voronoi区域（如图1所示）面积之和，f是xi所在三角形的数目，角θi如图2所示。

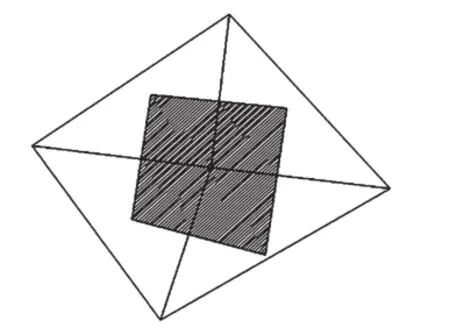
图1 Voronoi区域

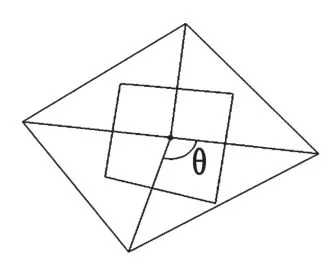
图2 三角网格上的微分算子

曲面网格如图3所示，点云如图4所示。

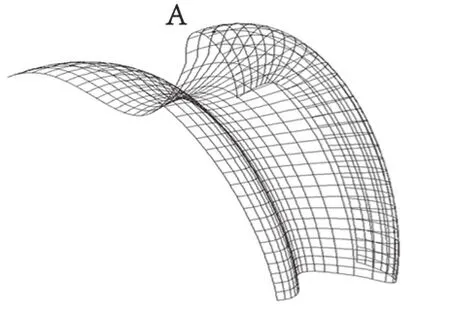
图3 曲面网格

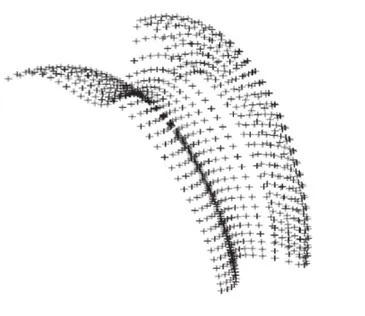
图4 点云

3 结语

刀具轨迹生成数控编程的核心工作是生成刀位轨迹，然后将其离散成刀位点，经后置处理产生数控加工程序。目前，在自由曲面加工中存在如下一些走刀方式，参数线法、平行截面法、类型螺旋法、等距偏置法和空间填充法，为用户提供了多种选择。不同的刀具轨迹，针对不同的曲面表面加工质量不同。以面曲率作为自由曲面复杂程度的评判依据可以清楚描述曲面以不同的刀具加工时难度的大小，并且可以以此针对性地选择编程策略和加工参数，以保障较高的加工质量。

基于自由曲面上点云通过曲面上点的计算曲率，过程较为简单且适用性强，能够用于曲率变化大的自由曲面的局部曲率计算，对工程师的加工策略安排有一定的指导作用。

[1]王奎武，陈发来，陈意云.基于点表示的曲面曲率计算方法[J].小型微型计算机系统，2005，（5）：813-817.

[2]Meyer M，Desbrun M，Schröder P，et al.Discrete Differential-Geometry Operators for Triangulated 2-Manifolds[J].Mathematics & Visualization，2002，6（8-9）：35-57.