基于订单拆分生产的MTO企业生产调度及算法研究*

姜 康 咸 凯 郝 宇

(合肥工业大学汽车与交通工程学院，安徽 合肥 230009)

随着工业化进程的不断加快，消费者的需求不断变化，企业在激烈的市场竞争中也必须适应消费者需求的变化。但是面对多变的消费需求，企业往往难以安排相应的生产或做出合理的订货决策，易出现供需不匹配的现象。在这种情况下，MTO模式由于其具有机动、灵活的特点，且能有效避免企业错误估计消费者需求导致供需不匹配的现象，而被越来越多的企业所采用[1]。

在MTO生产模式下，生产调度方案是影响企业利润的重要因素，引起了国内外学者与企业管理人员的深入研究。初红艳等人采用多智能体技术建立基于加工单元的制造车间调度系统结构，并采用遗传算法来确定工件的合理加工工序及各工序所用设备[2]。张铁男等人研究了生产资源受限情况下的车间调度问题，并提出了优化车间调度的方案[3]。刘红军等人研究了车间调度的本质，提出了一种基于GA-SA-TS算法的车间调度方法，三种算法相互结合避免了遗传算法局部搜索能力差和易早熟的缺点，大大提高了调度模型求解结果的准确性[4]。Chen等人研究了静态和动态生产环境下订单排产问题，并建立了求解订单排产顺序的数学模型[5-6]。Oguz等人针对单机环境提出订单排产的决策模型，设计了求解方法并将求解结果用于车间调度[7]。JC Tay，NB Hod等人指出传统的派工规则由于考虑不周全导致了企业绩效较低，并通过遗传进化的方法合理安排订单的加工顺序[8]。刘亮等人将APS系统和MES系统进行集成,从软件系统集成的角度研究了生产计划和调度方法[9]。虽然目前对车间调度研究较多，但是当前的研究存在以下问题：(1)在研究车间级的调度方案时，研究只着重于产品的工序调度，忽略了订单排产调度问题；(2)对订单排产的研究大多是在企业级调度层面，这种企业级的订单排产调度过于粗放；(3)对订单排产调度的研究多是基于订单不可拆分生产的原则进行的。当多个订单中出现一个订单量较大的订单时，传统的调度方案易导致较小的订单提前完工或延期交付，从而增大加工成本。因此，针对MTO企业车间调度问题应进行深入研究，建立适应于MTO企业的车间调度方案并设计有效的求解方法。

本文在深入调研MTO企业生产特点的基础上，提出了包括订单排产和产品工序调度的MTO企业车间二级调度方案，并科学筛选影响订单排产的因素，基于订单可拆分生产的原则，建立了用于车间订单排产的非线性规划模型。为了克服遗传算法容易陷入局部最优解和非线性寻优算法对初始解要求高的缺点，本文运用基于非线性寻优的遗传算法求解车间订单排产模型。

1 车间二级调度方案

在综合考虑MTO企业车间生产特点的基础上，根据实际情况可将车间的一个计划期划分为若干个计划时段，建立车间二级调度方案——订单排产调度和产品工序调度：前者负责整个计划期内的宏观排产；后者负责各个计划时段的加工调度。

1.1 车间级订单排产调度

车间级订单排产调度是指企业在计划期开始时，根据各订单的规模、交货期以及其它经济参数安排各订单的生产计划，使得企业的整体利润最大。传统的订单生产策略，如：先到先服务(FCFS)策略以及最早交货期优先(EDD)策略，每个订单都是连续生产的且订单一旦投入生产不能中断订单生产。在这种情况下，如果存在订单量较大的订单时，在综合排产时往往会出现其他订单提前完工或延期的现象，从而导致企业的相关成本增大。

基于订单可拆分的车间级订单排产调度，会根据车间以及订单的信息，合理地将订单安排到计划期内的各个时段上。在生产过程中可以根据需要将某些订单拆分生产，且在计划期内的各计划时段上可以同时生产多个订单。基于订单可拆分生产的车间级订单排产调度，可以有效减少因个别订单过大导致其他订单无法按时交货的情况，同时降低其他订单因提前完工而造成的不必要的库存成本。

1.2 车间级工序调度

车间级工序调度负责将一个计划时段内的所有工件的工序合理地分配到各设备上，使得在一个计划时段内的生产时间最短，缩小生产成本，达到增大企业生产利润的目的。

当前对车间级工序调度的研究已经十分深入，并且在MTO企业得到了广泛应用。大多数研究是在考虑不同影响因素的基础上，建立工序调度数学模型并通过算法对模型进行求解，最后根据求解结果进行调度。

1.3 调度流程

由图1可以看出，订单被安排到车间之后，一方面，车间需要进行相关生产资源的准备；另一方面，需要根据车间接受的各订单以及车间自身信息，合理地进行排产调度以及工序调度，达到最小化生产成本、提高企业利润的目的。由于对车间级工序调度的研究十分深入，因此本文着重于研究车间级订单排产调度。

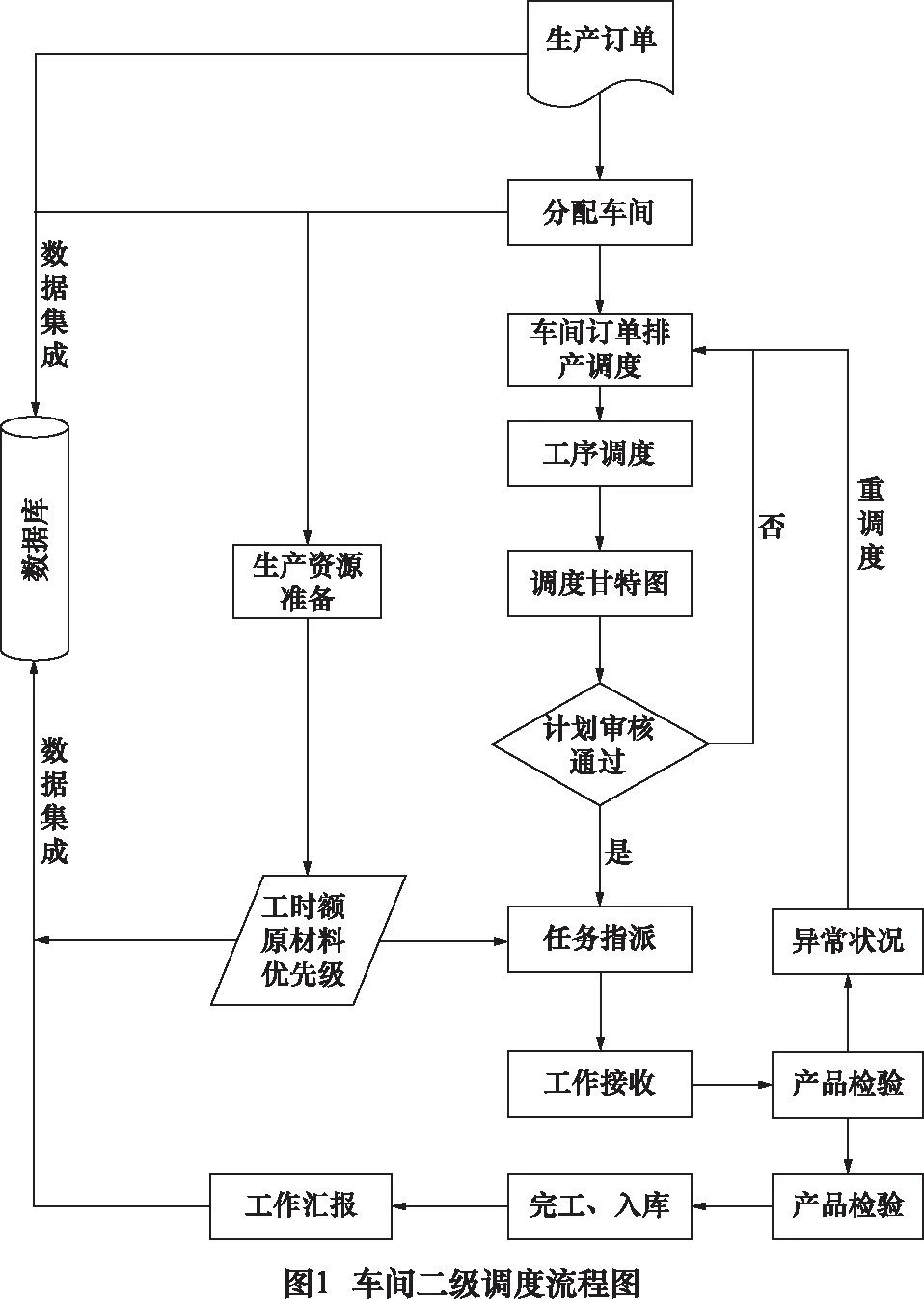
2 车间级订单排产调度模型

2.1 因素选取

影响订单生产调度的因素众多，因此需要对这些因素加以分析，科学、系统、完善地选取合适的因素进行建模。企业的首要目标是创造利润，企业的生产能力、生产成本、库存成本是影响企业获利的直接因素。但是企业利润的大小不仅仅取决于企业自身的情况，订单本身也是影响企业利润的关键因素，例如订单大小、订单价格、交货期、延期惩罚、顾客的潜在价值等[10]。因此可将影响订单生产调度的因素分为两个层次共8个指标(见图2)，在建模的过程中需要从这些因素的角度进行分析和考虑。

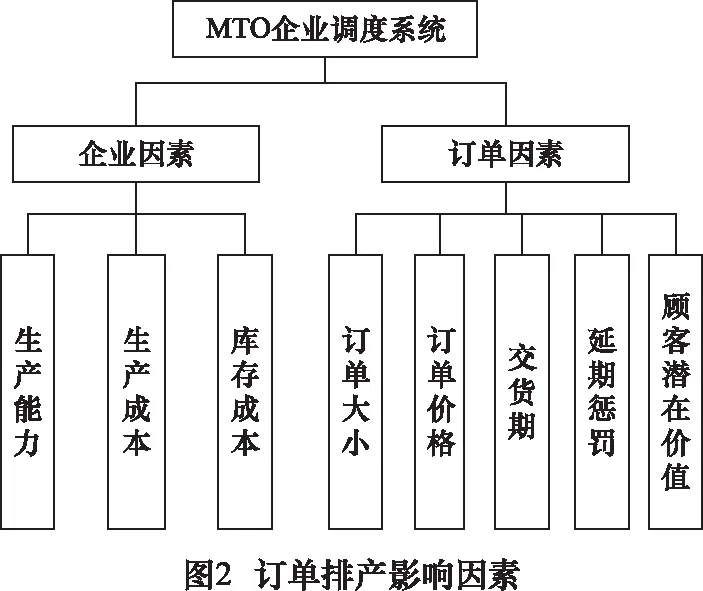
2.2 模型假设与问题描述

为了降低建立模型的复杂度，根据车间级订单排产调度特点，本文进行如下的假设：

(1)企业生产能力固定，每个计划时段内的产出不能超出企业的生产能力。

(2)订单可以提前完工，但不能提前交货。如果订单提前完工，那么订单必须在规定的交货期进行交付；如果订单没有提前完工，那么订单在加工完成后必须立即交付。

(3)客户只关心订单能否按期交货，不关心生产过程中订单是否拆分生产。

基于订单可拆分生产原则以及上述假设，车间级订单排产调度问题可以描述为：

在企业最大生产能力A约束下，将订单O={O1,O2,O3,…,On}合理分派到计划期内各计划时段上；在进行订单分配的时候，可以根据订单量和交货期的需要将订单拆分生产以获得更高的利润。

2.3 模型建立

根据上述假设，基于订单可拆分生产的原则，建立如下所示的车间订单排产调度模型。

Li表示订单i的大小(件)；Mi表示订单i的单位产品扣除生产成本的利润(元)；Vi表示订单i的潜在价值；TDi表示订单i的延期时间；Di表示订单i的单位产品延期惩罚系数(元)；Rit表示订单i在第t计划时段的库存占用量；Wi表示订单i的单位产品库存成本(元)；φ表示每次调整车间生产任务的成本(元)；Sit表示订单i在第t时段的状态，1为生产，0为不生产；TOi表示订单i的理论交付期；TRi表示订单i的实际交付期；TEi表示订单i的完成时间；Ait表示订单i在Tt时段占用企业的生产能力(件/计划时段)。

目标函数是考虑在扣除延期惩罚、库存成本以及由于订单拆分生产造成的企业设备调整费用之后的企业利润(包括顾客的潜在价值)；式(1)表示在当前时段所有正在生产的订单所需要的生产能力之和小于企业的最大生产能力；式(2)表示每个订单必须在计划期内完成；式(3)表示订单i的实际完成时间等于整个计划期上订单最后一次生产所在计划时段；式(4)表示订单i的延期时间；式(5)表示订单i的实际交货期，如果订单没有延期，则等于订单的理论交货期，否则等于订单的实际完工时间；式(6)表示订单i在t时段的库存量，企业并不是只将提前完工订单的全部产品放入仓库，也会将未完成订单但已完工的产品放入仓库；式(7)表示顾客的潜在价值，是关于延期时间TDi的减函数；式(8)表示订单i在第t时段的状态，1为生产，0为不生产。

2.4 模型分析

本文所建立的调度模型属于非线性规划模型。非线性规划问题是一个NP-hard问题，目前常用的求解方法有模拟退火方法、遗传算法、粒子群算法、非线性寻优算法等，这些算法在不同的领域均得到了成功应用。但是它们也存在着自身的缺点：模拟退火算法搜索过程缓慢；遗传算法虽然搜索速度快，但是容易陷入局部最优解；粒子群算法对离散问题处理不佳，容易陷入局部最优；非线性寻优算法搜索速度慢，对初始解要求高。考虑到在实际的工业生产中，需要快速得到调度结果，因此遗传算法适合用来解决这个问题。同时，为了解决遗传算法容易陷入局部最优解的缺点，本文在深入研究非线性规划问题常用的求解方法的基础上，将遗传算法和非线性寻优算法结合起来求解订单排产调度模型。

3 基于非线性寻优的遗传算法

3.1 基于非线性寻优的遗传算法

遗传算法搜索速度较快，但容易陷入局部最优解，适合在可行解集内进行大范围搜索；非线性寻优算法搜索速度慢，对初始可行解要求高，但结果较为精确，适合局部寻优[11]。

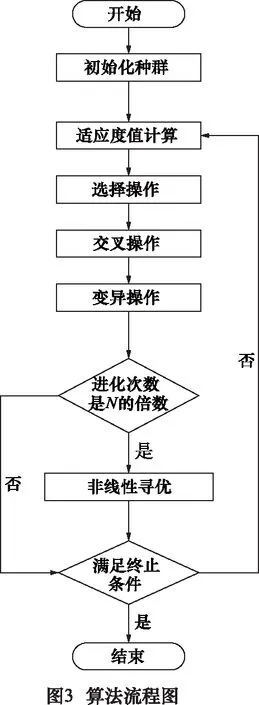
为解决遗传算法和非线性寻优算法的缺点，本文采用了一种基于非线性寻优的改进的遗传算法，首先利用遗传算法进行全局搜索，当达到进化代数N以及其整数倍时采用非线性寻优算法进行局部搜索，具体流程如图3所示。该算法结合了非线性寻优和遗传算法的优点而弥补了其不足，具有搜索速度快、结果精确度高的特点。

3.2 遗传算法设计

3.2.1 编码方式与适应度函数

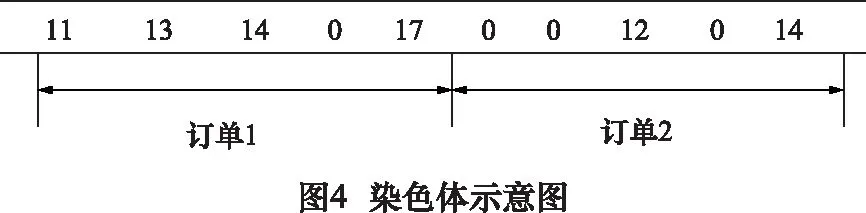
在本算法中设计了一种基于时序的整数编码方式。图4是一具有两个订单，每个计划期有5个时段的染色体。因为有2个订单且每个计划期有5个时段，所以在染色体中需要10个基因，前5个基因代表第一个订单，后5个基因代表第二个订单；每个基因上的数字，表示订单在相应时段上的生产数量。

本文将模型的目标函数作为遗传算法的适应度函数。

3.2.2 遗传算子

选择：采用比例选择算子执行选择操作。

交叉：采用改进的两点交叉策略：选择父染色体中相同订单编号对应的基因，互换位置进行交叉。如图5所示，P1和P2是具有3个订单的父染色体，选择P1和P2中订单2对应基因，互换位置进行交叉，得到子染色体C1和C2。

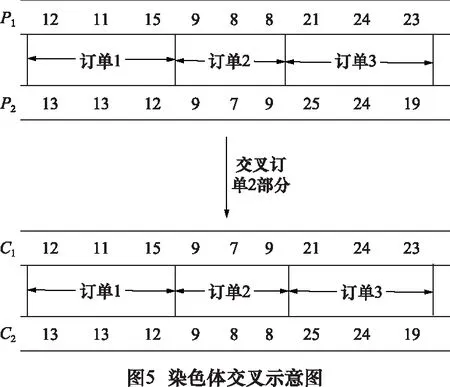
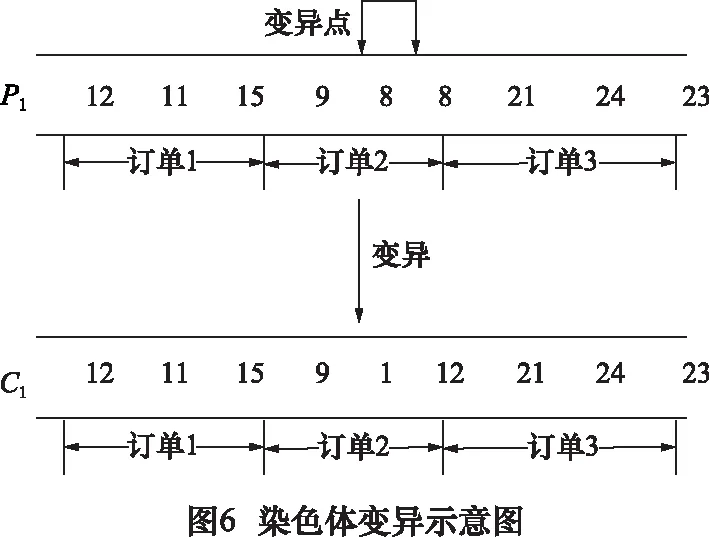
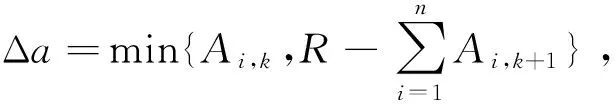
3.2.3 遗传算法参数设置

启发式遗传算法作为人工智能领域中用于解决最优化问题的一种搜索算法，其参数的设置至关重要。本文在查阅相关文献[12-15]的基础上，结合多次实验的结果确定了本问题中遗传算法的最优参数:种群数为50，交叉概率为0.6，变异概率为0.01，采用精英策略。种群每进化N=10代进行一次非线性寻优。

3.3 经典非线性寻优算法

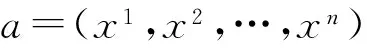
本文非线性寻优算法采用梯度下降法求解，利用目标函数以及约束函数信息，从给定的初始点开始，在满足约束条件下，沿目标函数梯度下降的方向迭代，逐步收敛到最优解。多维优化问题一般情况下会存在多个局部最优解，所以本文将非线性寻优算法用作局部寻优。

4 调度实例

为了便于直观分析调度结果，在本调度实例中假设各订单的单位产品的利润、单位产品延期惩罚、单位产品库存成本以及客户潜在价值均相同。

考虑3个订单，一个计划期有7个计划时段，企业最大生产能力为35单位产品情况下订单排产调度问题。订单具体信息如表1所示：订单1规模较大，交货期较晚，如果调度不当，容易导致订单2和订单3的延期交付或提前完工，造成不必要的延期惩罚以及库存成本，减少企业利润。

运用改进的遗传算法对该问题进行求解，得到遗传算法进化曲线(见图7)以及订单排产结果(见表2)。

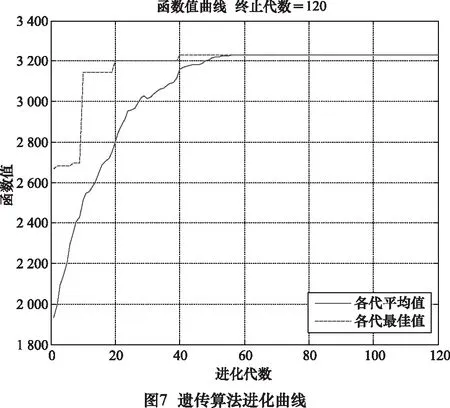
如图7所示，随着进化代数的增大，种群中最优个体的适应度函数值(即企业利润)不断增大；当进化代数达到60代左右时，种群收敛到最优个体。由于种群每隔10代进行一次非线性寻优，所以在第10、20、40代，种群最优个体适应度函数出现阶梯式增长，说明了基于非线性寻优的遗传算法的有效性。

表1 订单信息表

订单标号订单大小/件交货期/时段单位产品利润/元单位产品延期惩罚/元单位产品库存成本/元客户潜在价值/元订单1110718737订单252318737订单364518737

表2 基于订单拆分的调度结果

订单编号第1时段/件第2时段/件第3时段/件第4时段/件第5时段/件第6时段/件第7时段/件利润/元订单10003463535订单2017350000订单316180129003230

表3 基于EDD的调度结果

订单编号第1时段/件第2时段/件第3时段/件第4时段/件第5时段/件第6时段/件第7时段/件利润/元订单100024353516订单2351700000订单301835110002890

如表2所示，由于订单1规模较大且交货期较晚，所以在第1时段至第3时段并未安排生产，第4至7时段大量生产；由于订单2规模较小且交货期较早，所以订单2在第2、3时段大量生产；由于整个计划期的前半部分大量生产订单2，后半部分大量生产订单1，所以订单3根据实际情况进行了拆分生产。

根据EDD原则进行车间级订单排产调度，调度结果见表3。由表3可知，由于订单不可拆分生产，导致了订单2和订单3的提前完工，增大了库存成本，进而导致了整体利润的降低。

通过对车间级订单排产调度进行仿真以及其与传统调度方法的对比可以发现：基于订单可拆分生产的调度方案，由于其可以根据订单以及车间信息对订单的生产顺序进行合理规划，因此可以有效减少各订单的提前期或延期时间，从而减少生产成本，增大企业利润；传统的EDD调度方案由于订单不可拆分，订单一旦投入生产，在生产过程中不得中断订单的生产，易增大订单的库存成本或延期惩罚，从而降低企业利润。

5 总结与展望

针对MTO企业生产调度问题，本研究做了大量工作：

(1)本文在深入研究MTO企业车间调度特点的基础上，设计了MTO企业车间二级调度方案。

(2)通过科学选取影响订单排产调度的变量，基于订单可拆分生产的原则，本研究建立了车间级订单排产调度模型。

(3)将非线性寻优算法和遗传算法相互结合来改进遗传算法，将改进的算法应用于求解车间订单排产调度模型，并通过算例验证了该算法的有效性。

当前对MTO企业调度的研究仅从车间调度的角度出发考虑问题，今后应当将订单接受与订单调度联合考虑，使企业订单接受决策和车间制造有机结合以提高企业利润。

[1]范丽繁. 基于收益管理的MTS和MTO企业的供需管理研究[D].成都：电子科技大学, 2012.

[2]初红艳, 曹全军, 费仁元. 基于加工单元的制造车间的生产调度研究[J]. 北京工业大学学报, 2006, 32(8):730-736.

[3]张铁男, 韩兵, 于渤. 生产能力约束条件下的柔性作业车间调度优化[J]. 系统工程理论与实践, 2011, 31(3):505-511.

[4]刘红军, 赵帅, 赵雷. 一种基于GA-SA-TS算法的车间调度方法的研究[J]. 制造技术与机床, 2012(3):120-123.

[5]Kejia Chen, Ping Ji. A mixed integer programming model for advanced planning and scheduling(APS)[J]European Journal of Operational Research, 2007,181(1):515-522.

[6]KJ Chen, P Ji. A genetic algorithm for dynamic advanced planning and scheduling (DAPS) with a frozen interval[J].Expert Systems With Applications, 2007,33(4):1004-1010.

[7]OgUz C, Salman F S, Yalçn Z B. Order acceptance and scheduling decisions in make-to-order systems[J]. International Journal of Production Economics, 2010, 125(1):200-211.

[8]Tay J C, Ho N B. Evolving dispatching rules using genetic programming for solving multi-objective flexible job-shop problems[J]. Computers & Industrial Engineering, 2008, 54(3):453-473.

[9]刘亮, 齐二石. 基于APS与MES集成的车间生产计划和调度方法研究[J]. 制造技术与机床, 2006(9):24-28.

[10]唐丽春, 蔡晓毅. 供应链环境下订单优先权确定[J]. 系统工程理论与实践, 2009, 29(9):41-46.

[11]史峰. MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社, 2011:17-26.

[12]Wu C, Chang C, Chu T. The optimization of parameters for target tracking filter by genetic algorithm and taguchi method [J]. Pakistan Journal of Statistics, 2012, 28(1):167-176.

[13]何大阔, 王福利, 贾明兴. 遗传算法初始种群与操作参数的均匀设计[J]. 东北大学学报:自然科学版, 2005, 26(9):828-831.

[14]刘克刚, 朱福喜, 朱碧颖,等. 遗传算法参数的动态优化方案[J]. 小型微型计算机系统, 2015(4):768-772.

[15]何大阔, 王福利, 贾明兴. 遗传算法初始种群与操作参数的均匀设计[J]. 东北大学学报:自然科学版, 2005, 26(9):828-831.