圆度误差对气体静压主轴回转精度的影响研究*

张国庆 于贺春 赵则祥 王文博 王仁宗

(中原工学院，河南 郑州 450007)

气体静压轴承由于其高精度、低摩擦等优点，在加工及测试装备中得到了广泛应用。根据气体静压轴承的工作原理，轴套内表面的形状误差会影响出气方向，而转子外表面的形状误差会影响气浮力作用在转子表面的方向，引起转子的自转、偏移和倾斜。转子表面的形状误差还会影响其质量分布，在同一回转平面内，转子质心偏离回转轴线，在转动时产生离心惯性力。由于转子由气浮力支撑，刚度较小[1]，该离心惯性力会使主轴产生一定的径向偏移。

针对圆度等形状误差对主轴回转精度的影响，国内外许多学者进行了相关研究。熊万里等[2]通过建立并计算液体静压主轴回转精度的动力学模型，揭示了不同因素对回转精度的影响规律。侯志泉等[3-4]对轴径形状误差进行研究，利用CFD动网格技术进行计算并结合试验，证实其对液体静压主轴的回转精度有一定影响。魏坤[5]利用自编软件对主轴轴颈的形位误差对主轴的回转精度的影响进行了分析。

本文将通过建立圆度误差对气浮力和离心惯性力的影响模型并进行分析，研究圆度误差对气体静压主轴回转精度的影响，为气体静压主轴零部件的设计、制造及装配提供一定参考。

1 模型的建立

非理想化的主轴其每一截面处的形状误差各异。本文为便于建模和分析，不考虑圆柱度误差，即假设主轴每一截面均有相同的形状和尺寸。

1.1 气浮力模型

在多孔质气静压主轴内，转子会受到来自每一个出气点的气浮力，在这些气浮力的综合作用下，转子会产生自转、偏移和倾斜。图1为多孔质气静压主轴某一截面的示意简图，外五边形ABCDE代表轴套轮廓，内五边形abcde代表转子轮廓，内外两个五边形之间的区域为气膜，点o为转子的理想圆心。

以A点为例进行分析：由于轴套一般为多孔质石墨材质，可以假设气体由轴套内表面的点A处喷出，作用在转子表面的点A′上，气体的方向与∠EAB的角等分线重合。图2为点A′处的受力分析图，Fd为来自于点A的气浮力，F1和F2为其分力，F1⊥F2，F1指向圆心o，其中F1=Fdcosθ，F2=Fdsinθ。

各点的气浮力Fd的大小采用式(1)的等效弹簧模型来计算[6]：

|Fd|=f-k(r-r0)

(1)

式中：f为主轴预承载力；k为气静压主轴气膜的刚度系数；r、r0为出气点处气膜的实际厚度和初始厚度。

从轴套内表面每一个出气点产生的气浮力Fd在转子上均会有一个作用点，每一作用点处的F2均会使转子产生旋转，由于在实际应用中，转子的转动由驱动系统控制，因此本文对F2不做考虑。每一作用点处的F1由于指向圆心，其合力ΣF1会使转子发生偏移。在转速为零或较低的情况下，转子有足够的时间进行调整，最终会稳定在ΣF1=0的位置。在图1中的初始状态，转子会有一个稳定位置，但当转子转动到下一角度后，由每一个出气点与转子上作用点之间的r发生变化，导致Fd改变，使ΣF1≠0，在ΣF1的作用下，转子会有一个新的稳定位置。

以此类推，转子在每一个转动角度下均会有一个不同的稳定位置，而这个稳定位置的不断变化，使转子在转动时产生回转误差。

本文假设转子在每一个角度下均能达到稳定位置，根据该原理进行建模和编程，计算每一角度下转子在达到偏移稳定后的圆心坐标，进而计算转子的回转精度。

1.2 离心惯性力模型

转子由于外圆柱面具有一定的形状误差，会使其在截面上的质量分布不均，在旋转时质心偏离回转轴线，产生离心惯性力。图3为转子某一截面基于极坐标网格化的示意图，假设每一点都有一个偏心质量，则由偏心质量产生的离心惯性合力F为：

F=Σmiω2ri

(2)

式中：ω为转子的角速度；mi为第i点的偏心质量，ri为第i点处质心的回转半径。

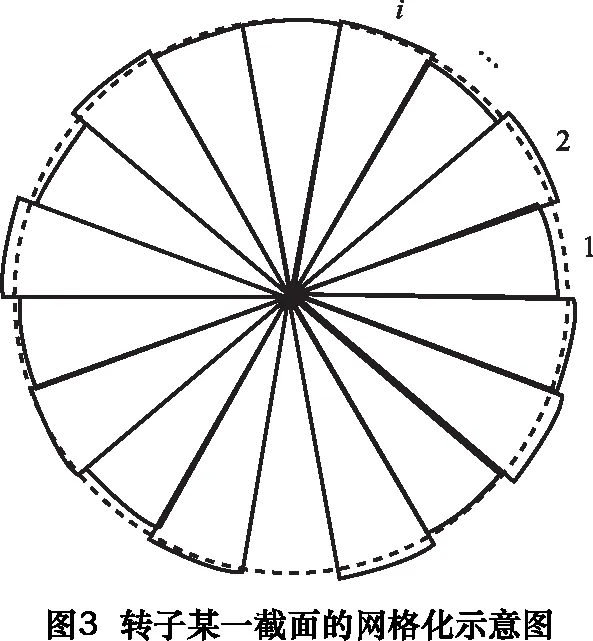
偏心质量mi由下式计算：

mi=ρπ(ri2-ro2)h/n

(3)

式中：ρ为转子材料的密度；h为转子的长度；ro为图3中虚线圆的半径；n为图3中转子截面的网格数。

整理式(2)、(3)可得，在离心惯性合力F的作用下，转子产生的径向偏移量Δe为：

Δe=|F|/k=|ρπhω2Σ(ri2-ro2)ri|/(nk)

(4)

式中：k为气静压主轴气膜的刚度系数。由式(4)可知，随着转速的增加，转子的径向偏移量会变大。本文将会计算主轴转速在0～6 000 r/min范围内(每隔1 000 r/min)，转子由于离心惯性力而产生的偏移。

2 模型的前处理

根据该主轴的设计标准，取预承载力f=1 000 N，刚度系数k=50 N/μm，气膜初始厚度r0=10 μm，转子材料密度ρ=7.75 g/cm3，转子长度h=240 mm。

模型计算所需要的轴套和转子的圆度误差数据来自Talyrond 585LT-500圆柱度仪对一套多孔质气静压主轴的检测结果。即对主轴的轴套和转子的不同位置分别测量4个截面，其中轴套和转子的截面位置是相对应的。图4为转子的检测过程，图5a和5b为第一个截面处轴套和转子的测量结果。轴套和转子的4个截面的圆度误差测量数据见表1(算法为最小二乘)。本文将利用这4组数据模拟4个主轴，然后分别进行建模计算。

Taylor 585LT圆柱度仪的标准采样点数为18 000 点/r，在模型1中为减小计算量，将轴套和转子的原始数据每100点取一个平均值生成新数据，然后再输入模型中进行计算，表2为利用新数据计算出的轴套和转子的圆度误差(算法与表1相同)；模型2则直接采用原始数据进行计算，此时网格数n=18 000。

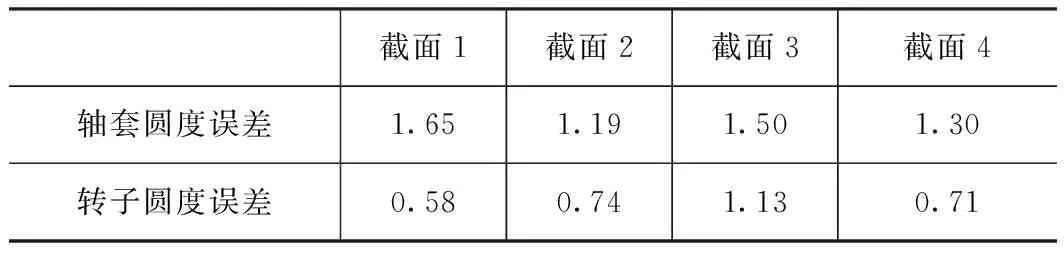
表1 轴套和转子的圆度误差A μm

表2 轴套和转子的圆度误差B μm

3 计算结果与分析

3.1 气浮力模型计算结果与分析

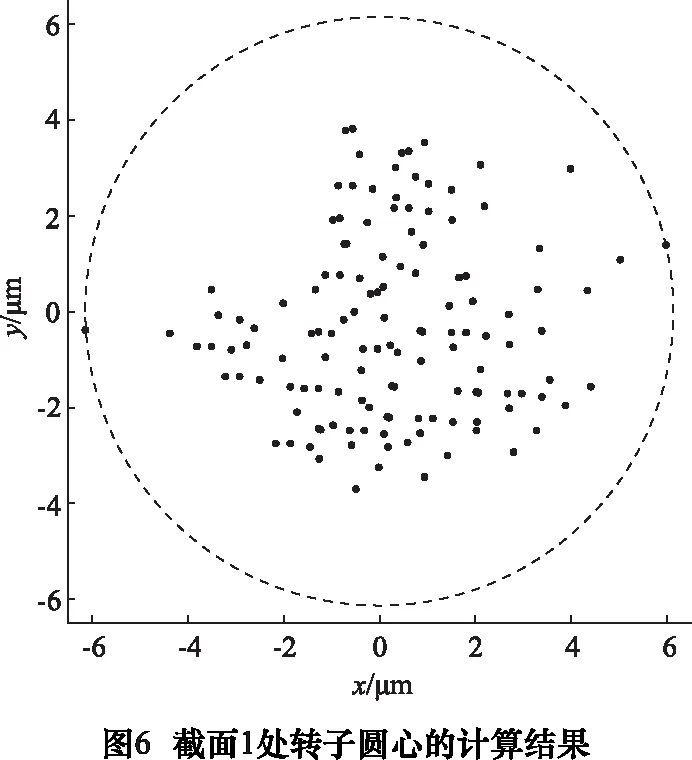
图6为采用轴套和转子截面1处的数据进行计算的结果。图中的实心点代表不同转动角度下转子圆心的位置，图中的圆为这些点的最小包围圆。采用不同截面处的轴套和转子数据进行计算所得转子圆心位置的最小包围圆直径见表3。

表3 最小包围圆直径计算结果 μm

表3中的数值仅能反映圆心的波动范围，对单个截面而言，由于圆心是在二维空间内波动的，其最小包围圆直径并不能准确反映主轴回转精度。因此，为了进行回转精度研究，需要进行模拟测量。

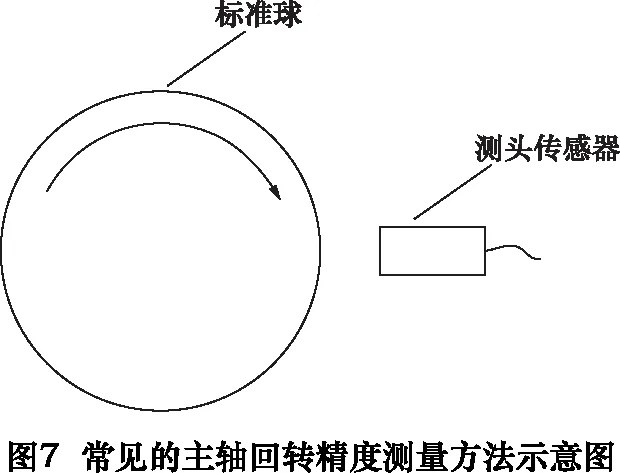
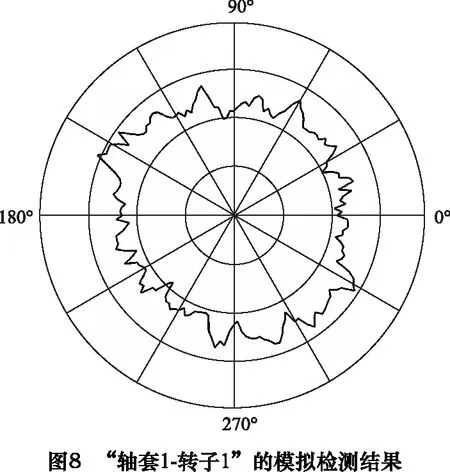
目前常见的主轴回转精度的测量方法是在转子上安装一个标准球，然后用测头传感器测量，如图7所示[7]。基于此方法进行建模，采用理想圆作为标准球，模拟的“轴套1-转子1”处的测头检测结果如图8所示，采用不同轴套和转子数据进行模拟测量的主轴精度误差见表4。

根据表2和表4中的数据，计算每一个主轴回转精度与其对应的轴套和转子圆度误差的比值k。对轴套而言，0.023

表4 模拟的主轴回转精度测量结果 μm

3.2 离心惯性力模型计算结果与分析

表5为采用不同转子数据进行计算的，不同转速下由离心惯性力引起的主轴偏移量。由表5可以看出，离心惯性力对主轴回转精度的影响较大，且随着转速升高，其影响显著增大。

表5 不同转速下的主轴偏移量 μm

4 结语

本文建立了两个基于圆度误差的理想模型，采用圆柱度仪测量的数据进行计算，通过对计算结果进行处理和分析，得出以下结论：

(1)在多孔质气体静压主轴中，轴套和转子的圆度误差会使气浮力分布不均，但由此产生的不平衡气浮力很小，对主轴回转精度影响很小，基本可以忽略。

(2)转子外圆表面的圆度误差会产生一定的离心惯性力，而该力对主轴回转精度的影响较大，不可忽略。在本模型所限定的理想前提下，离心惯性力会显著影响主轴在高转速下的回转精度。

(3)若气体静压主轴的工作转速较高，则对其转子外圆表面的圆度误差应有较高要求，而对其轴套内表面的圆度误差要求较低。

[1]周亮, 王宝瑞, 阳红. 微小间隙空气静压主轴角刚度分析与实验[J]. 制造技术与机床, 2016(12):40-44.

[2] 熊万里, 侯志泉, 吕浪. 液体静压主轴回转误差的形成机理研究[J]. 机械工程学报, 2014, 50(7):112-119.

[3] 侯志泉, 熊万里, 吕浪,等. 轴颈形状误差对液体静压主轴回转精度的影响[J]. 机械工程学报, 2016, 52(15):147-154.

[4] 侯志泉. 基于CFD动网格方法的液体静压主轴回转精度机理研究[D]. 长沙：湖南大学, 2013.

[5] 魏坤. 机床主轴回转精度的数字化建模与分析方法[D]. 重庆：重庆理工大学, 2013.

[6] 郑茂建. 基于CFD和转子动力学静压气体轴承回转精度联合仿真分析[D]. 哈尔滨：哈尔滨理工大学, 2016.

[7] Eric R Marsh. Precision spindle metrology[M]. Destech Pubns Inc, 2008.