Markov跳变系统有限短时间控制研究综述

曹智茹，牛玉刚*，宋 军，何舒平

(1.华东理工大学 信息科学与工程学院，上海 200237；2.安徽大学 电气工程与自动化学院，安徽 合肥 230601；3.安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230601)

随着现代控制理论的发展，研究人员开始用随机模型来描述工业生产中出现的各种复杂过程.环境改变、内部元件损坏及人为干预等因素的影响，使确定性的系统模型已不能准确描述工业生产过程，这时就需要用分段系统或跳变系统来描述.Markov跳变系统(Markov jump systems, 简称MJSs)是一类时间和事件共同驱动的混合系统，它用离散的模态表示不同的子系统，而各子系统又含有连续时变的状态变量，这类系统相对仅含有状态变量而无模态变化的一般系统来说，能够更加准确描述实际过程.

控制理论中，系统稳定性是系统控制过程的关键问题.Lyapunov渐近稳定性以假设工作时间无限长为前提，描述系统状态的渐进变化，即关注系统的稳态性能.然而，对于一些实际工程，人们更关心有限(或短暂)时间内系统的状态变化，如导弹系统及卫星姿态的调整.因此，有限短时间稳定(finite-time stability, 简称FTS)在一定程度上变得非常重要，极具研究意义.需要强调的是，由于Lyapunov稳定性和有限短时间稳定性是相互独立的两个概念，二者关注重点与研究方法也不同.

笔者对近年来Markov跳变系统的有限短时间控制问题进行综述.首先，阐述Markov跳变系统的稳定性、鲁棒控制及滤波方法；然后，介绍有限短时间稳定性的基本概念及目前Markov跳变系统有限短时间控制的研究现状；最后，从Markov跳变系统模型及有限短时间控制方法两个角度，分别提出Markov跳变系统有限短时间控制未来潜在的研究课题.

1 Markov跳变系统

1.1 Markov跳变系统模型

许多工业过程中，由于外界环境的突然变化、内部各子系统间连接方式的改变、非线性对象工作点范围的变化、元件损坏及人为干预等，系统结构会发生随机突变，这类系统称为混杂动态系统(hybrid dynamic systems, 简称HDS)[1].混杂动态系统可描述实际系统，如电力系统、生化系统以及经济系统等.

混杂动态系统既描述离散的事件动态，也描述连续的变量动态.切换系统(switched systems)描述一类特殊的混合系统，一个由多个子系统组成的切换系统，其系统状态的转移仅与该事件是否发生有关，而与该系统状态无关[2].一般地，切换系统由若干个子系统及一个切换信号构成，并通过切换信号在子系统间进行切换，以实现预定的性能指标.

Markov跳变系统是一种特殊的切换系统，该系统从一个模态切换到另一个模态的过程中没有固定的切换规则可以遵循，模态间切换是随机的，但这种随机切换符合一定的统计特性——各模态间的转移服从Markov跳变过程(Markov jump process)[3-4].因此，Markov跳变系统是一类特殊的随机系统，也称为随机Markov跳变系统(stochastic Markov jump systems, 简称SMJSs).

作为特殊的随机切换系统，Markov跳变系统模型可用来描述很多实际系统，如金融系统、网络控制系统、多旋翼姿态控制系统、机器人操作系统及同时涉及随机决策和连续控制的系统等.

下面介绍Markov跳变系统模型：

(1) 连续时间Markov跳变线性系统

连续时间Markov跳变线性系统的状态空间描述如下

(1)

其中：x(t)∈Rn，y(t)∈Rp，u(t)∈Rm分别为系统的状态向量、控制输出和控制输入；A(rt)，B(rt)，C(rt)均为适当维数的矩阵.{rt,t≥0}为有限集T={1,2,…,N}中取值的齐次Markov过程，具有如下性质

(2)

(2) 离散时间Markov跳变线性系统

离散时间Markov跳变线性系统的状态空间描述如下

(3)

其中：x(k)∈Rn，y(k)∈Rp，u(k)∈Rm分别为系统的状态向量、控制输出和控制输入；A(rk)，B(rk)，C(rk)均为适当维数的矩阵.{rk,k≥0}为有限集T={1,2,…,N}中取值的齐次Markov过程，具有如下性质

Pr{rk+1=j|rk=i}=πij，

(4)

由上面连续时间、离散时间Markov跳变线性系统模型可以看出，Markov跳变系统是由若干个子系统组成，不同的模态代表不同的状态空间，各模态间的跳变服从Markov过程.描述该Markov过程将来时刻的概率分布，仅依赖于现在时刻所给定的量，而与过去时刻的特性无关，Markov跳变系统的这种特性又称为无后效性.

1.2 Markov跳变系统的分析与综合

自Markov跳变系统被提出以来，该系统便引起了控制领域学者的广泛关注，并取得了大量的成果，主要包括以下几个方面：

(1) 稳定性分析

Markov跳变系统稳定性源于矩稳定性(moment stability).1969年，文献[5]由矩稳定性推出几乎必然稳定性，使稳定性分析有了进一步的发展.文献[6]研究了Markov跳变系统的随机稳定(stochastic stability)，在均方稳定充分条件的基础上，进一步研究了系统均方指数稳定(exponential mean square stability)的充要条件.文献[7]和[8]分别对离散时间和连续时间的线性Markov跳变系统的几乎必然稳定进行了深入的研究.文献[9]给出了受Markov链和确定性切换影响时线性Markov跳变系统几乎必然稳定的充分条件.

对于含有不确定性参数的Markov跳变系统，文献[10]给出了与时变时滞有关的指数均方稳定的充分条件.文献[11]考虑了线性Markov跳变系统中含有影响系统状态和输入矩阵范数有界的不确定性，给出了系统几乎必然稳定的充分条件.文献[12]研究了含有多胞参数不确定的非线性Markov跳变系统的指数均方稳定问题，通过构造依赖系统状态和不确定参数的随机Lyapunov函数，给出了非线性Markov跳变系统指数均方稳定的充分条件.

上述讨论均是在系统的转移概率完全已知的条件下进行的，实际上，系统的转移概率很难完全已知.文献[13]对具有时变时滞的离散时间线性系统的稳定性问题进行研究，考虑转移率为完全已知和完全未知两种情况，利用时变时滞的上下界信息给出了系统随机稳定的充分条件.文献[14]和[15]分别对连续时间和离散时间Markov跳变系统进行了进一步的研究，考虑了转移概率完全未知的情况，利用线性矩阵不等式给出了系统随机稳定的充要条件.

(2) 鲁棒控制

Markov跳变系统的鲁棒控制一直是控制领域的热点问题.文献[16]研究了一类具有参数不确定性的非线性离散Markov跳变系统的状态反馈镇定问题，利用隐函数定理和奇异值分解给出了线性矩阵不等式算法，设计鲁棒状态反馈控制器使被控系统随机稳定.文献[17]则对一类同时具有混合时变时滞和参数不确定的非线性连续Markov跳变系统进行研究，基于线性矩阵不等式给出了鲁棒稳定的充分条件.

关于随机Markov跳变系统鲁棒控制的相关研究成果还包括H∞控制问题[18-24]、成本及耗散控制问题[25-26]、模糊控制问题[27-29]及最优控制问题[30]等.其中，H∞控制是Markov跳变系统鲁棒控制研究中最常用的控制方法，文献[18]研究了具有不确定转移概率的离散时间Markov跳变系统的H∞控制问题，当不确定转移概率是连续随机变化且部分未知时，使用高斯密度函数对随机变化的转移概率进行量化处理，设计状态反馈控制器保证闭环系统随机稳定并满足给定的H∞性能指标.同样针对具有不确定转移概率的离散时间Markov跳变系统，文献[19]进一步考虑转移概率具有多胞不确定性且时变的情况，设计鲁棒H∞控制器减弱执行器饱和带来的影响.上述工作只考虑了系统状态可测的情况，当系统状态不可测时，文献[24]通过模态依赖和参数依赖的Lyapunov函数设计了一个基于观测器的H∞控制器，使增广系统不仅能够随机稳定，还能满足规定的H∞性能.

(3) 滤波方法

实际物理系统中，由于干扰、不确定性等，往往不能直接测量系统的状态，而只能通过系统输出来间接估计，因此Markov跳变系统的滤波一直是控制界的研究热点，常用的滤波方法有Kalman滤波、最小方差滤波、峰值滤波[31]、H∞滤波[32-36]等.由于H∞滤波仅要求能量有界而不需要考虑外部噪声信息，该滤波方法在Markov跳变系统得到了广泛应用.文献[32]针对具有Markov过程的网络控制系统，考虑系统中含有范数有界不确定性和随机丢包现象，设计滤波器使系统满足H∞性能指标且具有无源性.考虑到转移概率信息不完整的情况，文献[33]研究了具有多胞型不确定性转移概率的Markov跳变系统H∞滤波问题，文献[34]研究了同时具有多胞型不确定性和不完整转移概率的Markov跳变系统的H∞滤波问题.当滤波器的模态与系统模态异步时，文献[36]使用T-S模糊方法对非线性Markov系统进行建模，设计异步滤波器保证增广系统稳定.

上述研究都是在Markov跳变系统的模态信息可获得的条件下进行的，但实际应用中，有些模态很难测量，这使得上述方法不能应用到实际中.文献[37]和[38]分别针对连续时间和离散时间的线性Markov跳变系统设计了不依赖模态的鲁棒H∞滤波器.对非线性Markov跳变系统，文献[39]对滤波器与系统模态异步问题进行研究，设计了不依赖模态的具有分段同步的异步H∞滤波器保证系统随机稳定.

2 Markov跳变系统的有限短时间控制

2.1 有限短时间控制

有限短时间稳定，是指一个有限的时间内，系统的状态轨线始终不脱离预先给定的范围[40].图1展示了一个2维系统的有限短时间稳定性在状态空间的变化[41].

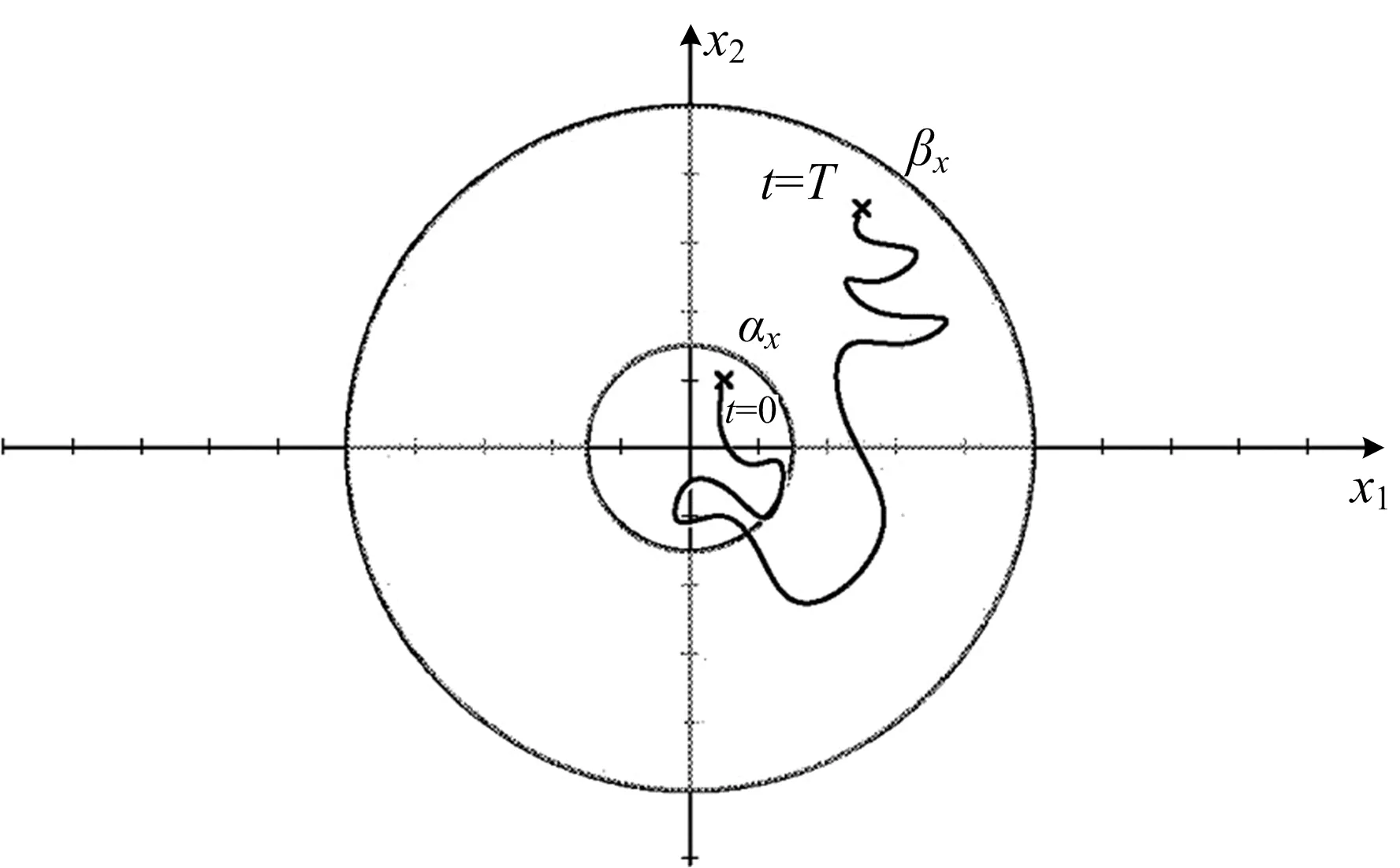
图1 一个 2维系统的有限短时间稳定性在状态空间的变化

在有限短时间稳定概念的提出之初，主要是针对如下自治系统

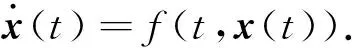
(5)

给定一个初始时间t0，一个正标量T，两个集合χ0和χt，如果系统(5)满足条件

x0∈χ0⟹x(t)∈χt,t∈[t0,t0+T] ，

(6)

则称该系统有限短时间稳定.但是，实际应用中，系统难免会受外界未知扰动的影响，于是文献[42]扩展了有限短时间状态稳定的概念，提出了有限短时间有界性(finite-time boundedness, 简称FTB).

对一个含有外部扰动的系统

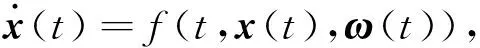
(7)

其中：ω(t)为外部干扰.给定一个初始时间t0，一个正标量T，两个集合χ0和χt，如果系统(7)满足条件

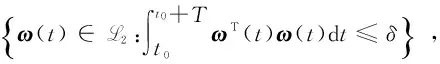
(8)

x0∈χ0⟹x(t)∈χt,t∈[t0,t0+T]，

(9)

则称该系统有限短时间有界.

文献[42]提出了输入输出有限短时间稳定(input-output finite-time stability, 简称IO-FTS)概念[43]，即给定一个确定的时间间隔，对于范数有界输入信号(即有界的外部扰动)，系统的输出在该时间间隔内不超过规定的阈值.

对含有外部扰动的动态系统

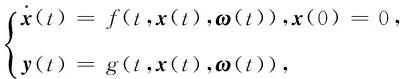
(10)

其中：ω(t)为外部干扰.

给定一个初始时间t0，一个正标量T，一个正标量δ，一个集合χt，如果系统(10)满足条件

(11)

W[t0,t0+T],δ⟹y(t)∈χt,t∈[t0,t0+T],

(12)

则称系统输入输出有限短时间稳定.

值得注意的是，有限短时间稳定性与Lyapunov渐近稳定性有很大的不同.前者关注系统状态的暂态性能、系统状态轨迹在给定时间间隔内的变化及有限短时间间隔内能量的变化，后者关注系统状态的最终稳态是否趋于零，因此有限短时间稳定是更有工程意义的稳定性概念.

2.2 Markov跳变系统有限短时间控制研究现状

有限短时间稳定问题因其具有重要的工程意义受到关注，Markov跳变系统的有限短时间控制也是近几年的研究热点.文献[44]首次给出连续和离散线性随机跳变系统有限短时间稳定、有界和镇定的定义，并设计出系统镇定控制器.文献[45]提出随机跳变系统有限短时间稳定相关概念后，进而将线性Markov跳变系统有限短时间稳定的主要论点推广到不确定随机Markov跳变系统，且研究了该类线性连续随机跳变系统基于状态反馈的有限短时间镇定问题.文献[46]研究了伊滕型随机Markov跳变系统的输入输出有限短时间均方镇定问题，针对外部的有界干扰，设计控制器使系统输出在给定时间内能量的均方值不超过给定的阈值.文献[47]研究了一类具有高斯型转移概率的Markov跳变系统，利用高斯密度函数对转移概率中随机不确定元素进行量化处理，设计了系统模态依赖的控制器，使闭环系统有限短时间有界.

鲁棒H∞控制是常用的处理Markov跳变系统有限短时间控制问题的方法.文献[48]提出了一个新的Lyapunov函数的构造方法，减少了常规方法处理时滞问题带来的保守性，设计的H∞控制器能保证系统有限短时间稳定且满足H∞性能指标.文献[49]则考虑Markov跳变系统的H∞静态输出反馈控制，引入与原系统状态和输出有关的新变量，给出闭环系统在特定的性能指标下的随机有限短时间有界的充分条件.文献[50]针对一类时滞锥型非线性系统，设计了系统的滑模控制器，并给出能保证闭环系统有限时间有界的充分条件.

对于Markov跳变系统的转移概率部分信息未知问题，文献[51]利用矩阵变换和Gron-wall不等式等方法，给出了有限短时间随机稳定的判定准则，设计出动态输出反馈控制器，使系统有限短时间镇定.文献[52]考虑了一类连续时间具有Markov过程的神经网络系统，利用已知的转移概率上下界信息设计控制器，研究系统有限短时间有界问题.文献[53]针对一类离散时间具有Markov过程的神经网络系统，使用自由权矩阵方法，讨论了系统随机有限短时间稳定和有限短时间有界问题.文献[54]则考虑了更一般的转移概率部分未知的情况，针对离散的Markov跳变系统，给出与转移概率边界信息有关的线性矩阵不等式，保证在该条件下系统状态在有限短时间间隔内不超出给定阈值.

上述研究工作均是在系统状态已知条件下进行的，但实际工程中，系统状态存在不可直接测得的情况，因此当Markov跳变系统的状态不可测时，基于观测器或估计器的控制器设计也受到关注.文献[55]针对一类具有时变时滞的连续时间线性Markov跳变系统，给出基于观测值新的有限短时间稳定的定义，设计状态反馈控制器使系统状态值在有限短时间内不超过给定值.对于离散时间线性Markov跳变系统，文献[56]考虑转移概率分段时变的情况，利用平均驻留时间设计切换信号，设计估计器对系统状态进行估计， 并设计H∞控制器使系统有限短时间有界且满足性能指标.文献[57]对具有不可靠通讯的离散时间线性Markov跳变系统进行研究，同时考虑分组丢包、时滞和传感器非线性，使用Lyapunov-Krasovskii方法，在有限短时间约束下，设计非脆弱状态估计器，使得增广系统有限短时间稳定.对于非线性Markov跳变系统，文献[58]利用T-S模糊模型对系统中的非线性部分进行建模，基于Lyapunov-Krasovskii泛函，构造基于观测器的状态反馈控制器，得到一个使Markov跳变系统有限短时间有界的充分条件，并使其在有限短时间内满足H∞性能指标.

3 展 望

从以上的研究现状可以看到，虽然Markov跳变系统有限短时间控制问题的研究已经取得很多成果，但是仍有不少问题值得探索.下面从Markov跳变系统模型及有限短时间控制方法两个角度，讨论未来可能的研究课题：

(1) 更复杂的Markov跳变系统模型

文献中一般讨论的是拥有固定转移概率的Markov跳变系统，而使用这种Markov跳变系统是难以准确描述复杂系统的.更复杂的Markov跳变系统模型有：2维Markov跳变系统[59]、半Markov跳变系统[60]、隐Markov跳变系统[61]、时变Markov跳变系统[62]，这些模型的有限短时间控制问题目前研究不多，将是后续值得研究的课题.

(2) 更多的有限短时间控制方法

针对Markov跳变系统的有限短时间控制问题，文献中广泛使用的均是基于线性反馈控制策略的有限短时间控制方法[63].最近几年，已有文献开始关注一些其他更加有效的有限短时间鲁棒控制方法，如文献[64]给出了基于滑模控制策略下的一般非线性系统有限短时间镇定方法，文献[65]基于非Lyapunov方法分析了中立型神经网络的有限短时间稳定性.但是，如何将这些新的智能控制方法推广到Markov跳变系统有限短时间控制领域仍有待进一步的探索.

参考文献：

[1] 莫以为, 萧德云. 混合动态系统及其应用综述[J]. 控制理论与应用,2002,19(1):1-8.

[2] 程代展, 郭宇窍. 切换系统进展[J]. 控制理论与应用,2005,22(6):954-960.

[3] 林元烈. 应用随机过程[M]. 北京: 清华大学出版社,2002.

[4] 刘次华. 随机过程[M].5版. 武汉: 华中科技大学出版社,2014.

[5] KOZIN F. A survey of stability of stochastic systems[J]. Automatica,1969,5(1):95-112.

[6] FENG X B, LOPARO K A, JI Y D, et al. Stochastic stability properties of jump linear systems[J]. IEEE Transactions on Automatic Control,1992,37(1):38-53.

[7] BOLZERN P, COLANERI P, NICOLAO G D. On almost sure stability of discrete-time Markov jump linear systems[C]//IEEE Conference on Decision and Control (CDC)，2004:3204-3208.

[8] BOLZERN P, COLANERI P, NICOLAO G D. On almost sure stability of continuous-time Markov jump linear systems[J]. Automatica,2006,42(6):983-988.

[9] BOLZERN P, COLANERI P, NICOLAO G D. Almost sure stability of Markov jump linear systems with deterministic switching[J]. IEEE Transactions on Automatic Control,2013,58(1):209-214.

[10] LI H Y, ZHOU Q, CHEN B, et al. Parameter-dependent robust stability for uncertain Markovian jump systems with time delay[J]. Journal of the Franklin Institute,2011,348(4):738-748.

[11] TANELLI M, PICASSO B, BOLZERN P, et al. Almost sure stabilization of uncertain continuous- time Markov jump linear systems[J]. IEEE Transactions on Automatic Control,2010,55(1):195-201.

[12] CARLOS E D S, COUTINHO D F. Robust stability of a class of uncertain Markov jump nonlinear systems[J]. IEEE Transactions on Automatic Control,2006,51(11):1825-1831.

[13] ZHANG L X, BOUKAS E K, LAM J. Analysis and synthesis of Markov jump linear systems with time-varying delays and partially known transition probabilities[J]. IEEE Transactions on Automatic Control,2008,53(10):2458-2464.

[14] ZHANG L X, BOUKAS E K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities[J]. Automatica,2009,45(2):463-468.

[15] ZHANG L X, LAM J. Necessary and sufficient conditions for analysis and synthesis of Markov jump linear systems with incomplete transition descriptions[J]. IEEE Transactions on Automatic Control,2010,55(7):1695-1701.

[16] SONG S, MA S P, ZHANG C H. Stability and robust stabilization for a class of non-linear uncertain discrete-time descriptor Markov jump systems[J]. IET Control Theory & Applications,2012,6(16):2518-2527.

[17] ZHU Y Z, ZHANG Q G, WEI Z L, et al. Robust stability analysis of Markov jump standard genetic regulatory networks with mixed time delays and uncertainties[J]. Neurocomputing,2013,110:44-50.

[18] LUAN X L, ZHAO S Y, LIU F.H∞control for discrete-time Markov jump systems with uncertain transition probabilities[J]. IEEE Transactions on Automatic Control,2013,58(6):1566-1572.

[19] SHI P, YIN Y Y, LIU F, et al. Robust control on saturated Markov jump systems with missing information[J]. Information Sciences,2014,265:123-138.

[20] MA H J, ZHANG W H, HOU T. Infinite horizonH2/H∞control for discrete-time time-varying Markov jump systems with multiplicative noise[J]. Automatica,2012,48(7):1447-1454.

[21] KARIMI H R. Robust delay-dependentH∞control of uncertain time-delay systems with mixed neutral, discrete, and distributed time-delays and Markovian switching parameters[J]. IEEE Transactions on Circuits and Systems I: Regular Papers,2011,58(8):1910-1923.

[22] ZHONG X G, HE H B, ZHANG H G, et al. Optimal control for unknown discrete-time nonlinear Markov jump systems using adaptive dynamic programming[J]. IEEE Transactions on Neural Networks and Learning Systems,2014,25(12):2141-2155.

[23] QIU J B, WEI Y L, KARIMI H R. New approach to delay-dependentH∞control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions[J]. Journal of the Franklin Institute,2015,352(1):189-215.

[24] YIN Y Y, SHI P, LIU F, et al. Observer-basedH∞control on nonhomogeneous Markov jump systems with nonlinear input[J]. International Journal of Robust and Nonlinear Control,2014,24(13):1903-1924.

[25] WANG Y Y, WANG Q B, ZHOU P F, et al. Robust guaranteed cost control for singular Markovian jump systems with time-varying delay[J]. ISA Transactions,2012,51(5):559-565.

[26] SHEN H, PARK J H, ZHANG L X, et al. Robust extended dissipative control for sampled-data Markov jump systems[J]. International Journal of Control,2014,87(8):1549-1564.

[27] WANG J W, WU H N, GUO L, et al. RobustH∞fuzzy control for uncertain nonlinear Markovian jump systems with time-varying delay[J]. Fuzzy Sets and Systems,2013,212:41-61.

[28] YE D, YANF X, SU L. Fault-tolerant synchronization control for complex dynamical networks with semi-Markov jump topology[J]. Applied Mathematics and Computation,2017,312:36-48.

[29] SHEN M Q, YE D. Improved fuzzy control design for nonlinear Markovian-jump systems with incomplete transition descriptions[J]. Fuzzy Sets and Systems,2013,217:80-95.

[30] LUAN X L, LIU F, SHI P. Neural network based stochastic optimal control for nonlinear Markov jump systems[J]. International Journal of Innovative Computing, Information and Control,2010,6(8):3715-3723.

[31] HE S P, LIU F. Robust peak-to-peak filtering for Markov jump systems[J]. Signal Processing,2010,90(2):513-522.

[32] MATHIYALAGAN K, PARK J H, SAKTHIVEL R, et al. Robust mixedH∞and passive filtering for networked Markov jump systems with impulses[J]. Signal Processing,2014,101:162-173.

[33] GONCALVES A P, FIORAVANTI A R, GEROMEL J C. Filtering of discrete-time Markov jump linear systems with uncertain transition probabilities[J]. International Journal of Robust and Nonlinear Control,2011,21(6):613-624.

[34] DONG H L, WANG Z D, HO D W C, et al. RobustH∞filtering for Markovian jump systems with randomly occurring nonlinearities and sensor saturation: the finite-horizon case[J]. IEEE Transactions on Signal Processing,2011,59(7):3048-3057.

[35] DONG H L, WANG Z D, GAO H J. DistributedH∞filtering for a class of Markovian jump non-linear time-delay systems over lossy sensor networks[J]. IEEE Transactions on Industrial Electronics,2013,60(10):4665-4672.

[36] YIN Y Y, SHI P, LIU F, et al. Fuzzy model-based robustH∞filtering for a class of nonlinear nonhomogeneous Markov jump systems[J]. Signal Processing,2013,93(9):2381-2391.

[37] SOUZA C E D, TROFINO A, BARBOSA K A. Mode-independentH∞filters for Markovian jump linear systems[J]. IEEE Transactions on Automatic Control,2006,51(11):1837-1841.

[38] COSTA O L V, BENITES G R. Robust mode-independent filtering for discrete-time Markov jump linear systems with multiplicative noises[J]. International Journal of Control,2013,86(5):779-793.

[39] WU Z G, SHI P, SU H Y, et al. Asynchronousl2-l∞filtering for discrete-time stochastic Markov jump systems with randomly occurred sensor nonlinearities[J]. Automatica,2014,50(1):180-186.

[40] WEISS L, INFANTE E. On the stability of systems defined over a finite time interval[J]. Proceedings of the National Academy of Sciences,1965,54(1):44-48.

[41] ELBSAT M N. Finite-time control and estimation of nonlinear systems with disturbance attenuation[M]. Milwaukee: Marquette University,2012.

[42] AMATO F, ARIOLA M, DORATO P. Finite-time control of linear systems subject to parametric uncertainties and disturbances[J]. Automatica,2001,37(9):1459-1463.

[43] AMATO F, AMBROSINO R, COSENTINO C, et al. Input-output finite time stabilization of linear systems[J]. Automatica,2010,46(9):1558-1562.

[44] 何舒平， 刘飞． Markov跳变系统的有限短时间状态反馈镇定[J]. 控制与决策,2009，24(1):91-95．

[45] HE S P, LIU F. Stochastic finite-time stabilization for uncertain jump systems via state feedback[J]. Journal of Dynamic Systems, Measurement, and Control,2010,132(2)：0345041.

[46] MA H J, JIA Y M. Input-output finite-time mean square stabilisation of stochastic systems with Markovian jump[J]. International Journal of Systems Science,2014,45(3):325-336.

[47] LUAN X L, SHI P, LIU F. Finite-time stabilisation for Markov jump systems with Gaussian transition probabilities[J]. IET Control Theory & Applications,2013,7(2):298-304.

[48] CHENG J, ZHU H, ZHONG S M, et al. Finite-timeH∞control for a class of Markovian jump systems with mode-dependent time-varying delays via new Lyapunov functionals[J]. ISA transactions,2013,52(6):768-774.

[49] SHEN M Q, YAN S, ZHANG G M, et al. Finite-timeH∞static output control of Markov jump systems with an auxiliary approach[J]. Applied Mathematics and Computation,2016,273:553-561.

[50] HE S P, SONG J, LIU F, Robust finite-time bounded controller design of time-delay conic nonlinear systems using sliding mode control strategy[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems,2017(99)：1-11.

[51] 张维海, 刘鹤鸣. 随机马尔科夫跳跃系统有限短时间控制[J]. 控制理论与应用,2015,32(3):334-340.

[52] HE S P, LIU F. Stochastic finite-time boundedness of Markovian jumping neural network with uncertain transition probabilities[J]. Applied Mathematical Modelling,2011,35(6):2631-2638.

[53] HOU L Y, CHENG J, WANG H L. Finite-time stochastic boundedness of discrete-time Markovian jump neural networks with boundary transition probabilities and randomly varying nonlinearities[J]. Neurocomputing,2016,174:773-779.

[54] SHEN M Q, YUAN Y H. Finite-time stabilization of discrete Markov jump systems with partly known transition probabilities[C]//International Conference on Mechatronics and Control (ICMC),2014:2420-2424.

[55] HE S P, LIU F. Observer-based finite-time control of time-delayed jump systems[J]. Applied Mathematics and Computation,2010,217(6):2327-2338.

[56] CHENG J, ZHU H, ZHONG S M, et al. Finite-timeH∞estimation for discrete-time Markov jump systems with time-varying transition probabilities subject to average dwell time switching[J]. Communications in Nonlinear Science and Numerical Simulation,2015,20(2):571-582.

[57] LI F, SHEN H, CHEN M S, et al. Non-fragile finite-timel2-l∞state estimation for discrete-time Markov jump neural networks with unreliable communication links[J]. Applied Mathematics and Computation,2015,271:467-481.

[58] HE S P, LIU F. Finite-timeH∞fuzzy control of nonlinear jump systems with time delays via dynamic observer-based state feedback[J]. IEEE Transactions on Fuzzy Systems,2012,20(4):605-614.

[59] ZHANG G C, TRENTELMAN H L, WANG W Q, et al. Input-output finite-region stability and stabilization for discrete2-D Fornasini-Marchesini models[J]. Systems & Control Letters,2017,99:9-16.

[60] ZHANG L X, TANG T, COLANERI P. Stability and stabilization of semi-Markov jump linear systems with exponentially modulated periodic distributions of sojourn time[J]. IEEE Transactions on Automatic Control,2017,62(6):2870-2885.

[61] COSTA O L V, FRAGOSO M D, TODOROV M G. A detector-based approach for theH2control of Markov jump linear systems with partial information[J]. IEEE Transactions on Automatic Control,2015,60(5):1219-1234.

[62] SONG J, NIU Y G, ZOU Y Y. Asynchronous output feedback control of time-varying Markovian jump systems within a finite-time interval[J]. Journal of the Franklin Institute,2017,354(15):6747-6765.

[63] 何舒平， 沈浩. 随机Markov跳变系统的有限短时间控制与综合[M]. 北京: 科学出版社，2016.

[64] SONG J, NIU Y G, ZOU Y Y. Finite-time stabilization via sliding mode control[J]. IEEE Transactions on Automatic Control,2017,62(3):1478-1483.

[65] ZHENG M W, LI L X, PENG H P, et al. Finite-time stability analysis for neutral-type neural networks with hybrid time-varying delays without using Lyapunov method[J]. Neurocomputing,2017,238:67-75.