原子磁力仪传感器高精度温控技术研究

张敬兴 ，王劲东 ，薛洪波

（1.中国科学院国家空间科学中心空间天气学国家重点实验室北京100190；2.中国科学院大学北京100049）

基于相干布居囚禁量子效应[1]的全光学原子磁力仪，是一种新型原子磁力仪。此类磁力仪相比较于传统的碱金属光泵磁力仪、He光泵磁力仪[2]等原子磁力仪，其突出特点就是利用全光学共振，传感器全部由光学元件构成，不需要额外的射频线圈，使得传感器做的很小，从而实现更高的空间分辨率[3]。同时也不存在因为射频线圈而引入的额外磁场噪声问题[4]，使原子磁力仪对外磁场的测量更加准确。为了进一步提高相干布居原子磁力仪的探测灵敏度和准确度，对原子气室的温度条件提出了严格的要求。开展原子气室高精度温度控制，是一种提高磁力仪探测灵敏度和精度的有效方法[5]。

1 原子磁力仪温控需求分析

基于相干布居囚禁效应的碱金属全光学原子磁力仪需要工作在原子蒸汽状态下，且对气体浓度有一定要求。它们是基于工作元素Rb87与光子相互作用的产生共振信号[6]，得出塞曼效应在原子能级上的频移来计算待测磁场值。对于磁力仪原子气室的温控主要基于以下两点考虑：其一，由工作元素铷的物理特性可知，Rb87熔点约为39oC，所以在常温下，气室内的气态原子数密度有限，使得其与双色光子作用的铷原子有限，从而产生的共振信号强度达不到最大幅值，根据文献[7]提出的在一定体积的原子气室内的饱和Rb原子在温度为250～298 K时原子数的变化曲线可以看出原子数随温度升高而递增，另外，德国波恩大学以及美国国家标准与技术研究院研究小组共同的研究结果[8]知共振信号幅度在气室温度为45oC时能得到最大的幅值。其二，塞曼频移是会随温度变化的[9]，所以温度的变化会导致测量结果不准确。塞曼频移随温度变化的影响可以通过采用双“暗态”测量模式很大程度消除，但是仍然会存在非线性的二阶塞曼频移等因素的影响。

综合上述，为了尽可能地克服温度影响，保证相干布居囚禁原子磁力仪的性能，对原子气室进行温控，使其工作在一个温度比较稳定且合适的温度环境下是提高测磁准确度和灵敏度的有效手段，本温控系统的温控范围设定为35～45oC，当原子气室工作在35oC的环境下，虽然此时没有达到铷的熔点，但此时由于铷原子的升华而使气室内含有一定数量的气态铷原子使其与光子相互作用，此时生成的共振信号是由有限的铷原子与光子的作用而形成，还可以通过加热增大气室内铷原子的数密度，进一步改善共振信号，提高测量精度[10]。综上，本系统设定稳态温度目标值是45oC，误差范围设定为±0.05oC。

2 温控系统工作方案

整个温控系统是基于FPGA平台，应用数字化PID控制算法，采用专用的加热驱动芯片，通过A/D转换器和PT1000铂电阻等构成一个闭环回路以达到对原子气室进行控温以及无磁加热的目的。如图1是该系统的原理图。

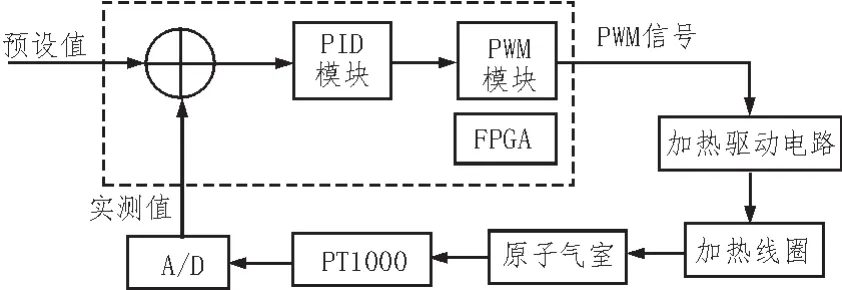
图1 温控系统原理框图

通过控制加热驱动电路给加热线圈通入的交流电流对其进行加热再通过热传导、热辐射给原子气室加热。在原子气室的外层是一种性能良好的绝热层，因此绝大部分的热量会被原子气室吸收。热电阻PT1000测量气室温度，反馈给A/D模数转换器采集实时温度值，与基准电压进行比较，通过数字PID和PWM模块控制加热驱动器输出电流，从而控制系统的加热功率。最终使得气室的温度最终可稳定在设定值，达到温控目的。温控系统的设计是只通过加热的方式控制温度，故气室的预设温度设置在工作环境温度的上限以上，同时，该系统还需要考虑到设计的低功耗要求。

3 被控对象的热仿真及热分析

3.1 被控对象建模以及热仿真

3.1.1 被控对象建模

应用Solidworks建模软件[11]建立被控对象，即磁传感器的三维模型。磁传感器加热模型的核心包括玻璃材质的原子气室、尼龙材料的气室外壳、以及导热性能良好的铝合金加热线圈以及传感器外壳。对模型进行基于有限元方法的热仿真[12]，需要对传感器三维模型网格划分。

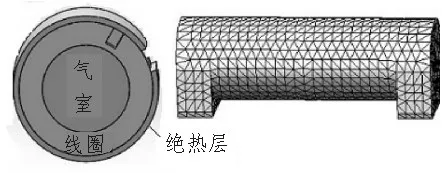
图2 传感器三维网格图

图2中左图是传感器外壳内部原子气室及其外围零件的三维模型，从里往外依次是原子气室、加热线圈、隔热层。右图是对模型进行网格化后的模型。

热传递过程主要有3种方式，即热传导、热辐射、热对流[13]。传感器工作时主要换热过程是传感器与固定用底座垫板之间的热传导以及内部各零件之间的辐射、传导换热，而忽略磁力仪外壳与空气的辐射传热和对流热传导。磁传感器内部的整个热传递过程如图3所示。

图3中加热线圈作为温控系统的热源为原子气室提供热量，同时传导给与其接触的绝热层，加热线圈分别向原子气室、和绝热层辐射热量，绝热层受热后向传感器外壳通过传导和辐射传递热，图中箭头方向表示热传递的方向。

图3 探头内部热流图

3.1.2 被控对象的热仿真

1）稳态仿真

为了确定被控对象的加热功率和热分布情况，需要对被控对象进行热力学稳态仿真。在-45～45oC工作环境温度范围内，通过给垫板底座指定不同的温度，设定被控对象的目标加热温度为45oC，设置相应的传热系数。得到在不同温度条件下所需的加热功率需求和被控对象的稳态热分布情况。图4所示为指定垫板温度为17oC时的稳态仿真结果。

图4 稳态热分布图

图4所示为磁传感器横向切面热分布结果，可以看出磁传感器原子气室的温度能比较好的稳定在45oC左右，而且原子气室温度梯度经仿真工具探测只有0.1oC，说明绝热层能达到很好的绝热效果，减少了气室对外界的温度耗散。根据不同的温度得到加热温度功率曲线如5图所示。

图5 稳态仿真温度功率曲线

2）瞬态仿真

被控对象的传递函数模型的确定，需要知道热仿真的加热时间响应曲线。瞬态响应在稳态响应的基础上，设置热仿真的初始加热温度为290 K（17oC），通过设定不同的仿真时长直温度达到稳态时的时间响应曲线。有限元仿真曲线如图6所示。

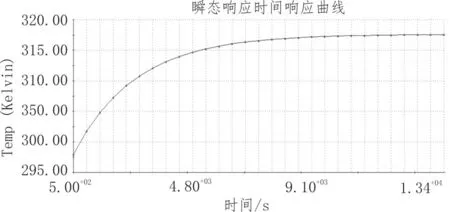
图6 瞬态温度响应曲线

根据时间响应曲线看出该被控对象的传递函数模型可以用一阶惯性系统来描述，本文应用Matlab对上述仿真结果进行曲线拟合，以确定模型中的热阻、热容等参数，进而得出被控对象的传递函数。

3.2 被控对象传递函数

由被控对象的热仿真结果可知，将系统作为一阶微分方程的集总参数系统来处理[14-15]，

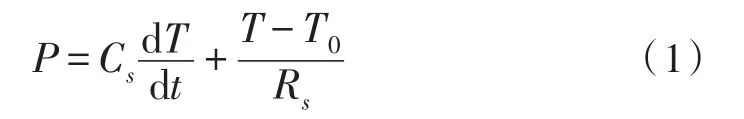
式中P为加热功率，Cs为系统总热容，Rs为系统总热阻，T0为环境温度，这里表示考虑热传导时给垫板指定的温度。在初始条件为T(0)=T0时，解得上述微分方程的解为：

当系统的目标温度设定后，加热功率由稳态热仿真的结果可以得到相应的值，也即可以视为常数，现在为了确切的知道被控对象的传递函数还需求出Cs、Rs两个系统相关参量，式中RsCs作为系统的加热时间常数τ0。运用Matlab基于式（2）对系统的瞬态仿真得到的温度时间相应曲线进行拟合，求出被控对象传递函数模型的相应参量，拟合采用最小二乘法。得到的仿真曲线如图7所示。

图7中的拟合结果中，图（a）的拟合曲线是基于最小二乘法得出的最佳拟合结果，图（b）是基于式（2）中惯性项的拟合验证效果，图（c）则是式中耗散项的拟合验证效果。仿真结果表明当加热时间常数τ0=2 109 J/W，耗散项PRs=28 K时最接近拟合结果，此时算出热阻Rs=21 K/W。（b）、（c）两图仿真结果进一步验证了由最小二乘法得出的拟合结果。对式（2）进行拉式变换后可得：

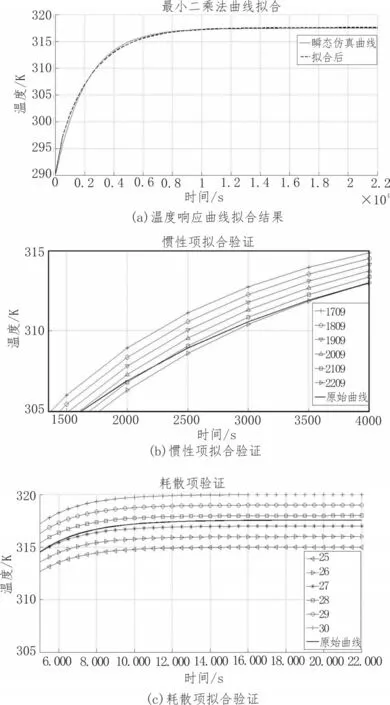
图7 时间响应曲线拟合结果

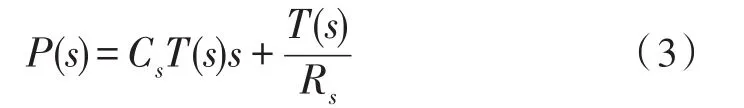
整理式（3）得到被控对象的传递函数：

根据拟合的结果计算出系统的两个参量值，Rs=21 K/W，τ0=2 109 J/W，便可得被控对象的传递函数。

4 控制算法及其仿真

4.1 控制算法介绍

温控系统运用PID控制算法，为了实现磁力仪的数字化以及避免因模拟器件带来的干扰，采用了数字式PID温控方式，在现有的FPGA数字平台上通过数字式PID算法模块实现温度控制。因此需要完成对模拟PID算法的离散化，离散化过程如下所示[16]：

其中T是对模拟信号的采样周期，k为采样系数，分别将上述两式代入到模拟式PID算法公式并整理得PID算法的数字化表达形式。

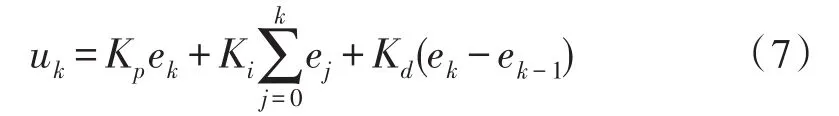
4.2 控制算法仿真

确定了被控对象的传递函数模型以及控制算法后，为了使得温控系统能在有限的功率范围内达到更好的控制效果，对控制算法进行仿真以确定最佳的控制参数（Kp、Ki、Kd），仿真使用Matlab的Simulink工具进行搭建[17]。根据温控算法原理，在Matlab中建立系统模型，如图8所示。

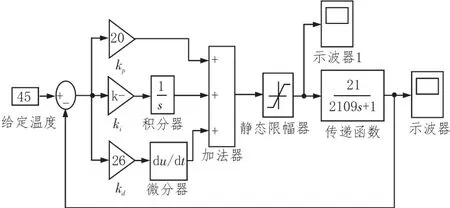
图8 控制算法仿真模型

模型中，给定温度与从被控对象采集来的实际温度值求误差值进而送入PID控制器，分别经过比例、积分、微分作用对误差值进行校正以逐步逼近设定值，温控系统的初始温度定为0oC，系统中加了一个静态限幅器，是为实际应用实现低功耗的目标。基于系统给定温度和功耗需求不断调整参数Kp、Ki、Kd，达到较为理想的控温效果。

图9中的（a）、（b）、（c）分别代表设定目标温度值分别为15oC、30oC、45oC时的控制算法的仿真结果，包括温度控制曲线、所需加热功率要求和温度稳定后的误差。表1所示是根据上图仿真结果的指标统计。

可知系统可以在预期较短的时间内将温度稳定在设定温度45oC，并且磁传感器温度的误差不超过±0.05oC，同时满足设计初预设的低功耗要求。

5 结 论

文中利用有限元分析软件完成了对原子磁传感器的三维建模并分别进行模型的稳态、瞬态热仿真得到相关热分布结果和时间响应曲线，据此求解了传感器的传递函数模型，对温控系统的控制算法的进行参数调试和仿真，结果表明，温控系统的温控温度误差值达到0.02oC，温度控制稳定度能够达到45±0.05oC的设计要求，确定了该温控方式是可行的，而且仿真结果显示该温控方法可以实现在限定低功耗条件下较快速的稳定传感器温度，为原子磁力仪传感器的高精度温度控制系统下一阶段的实际实现和试验调试提供了依据。

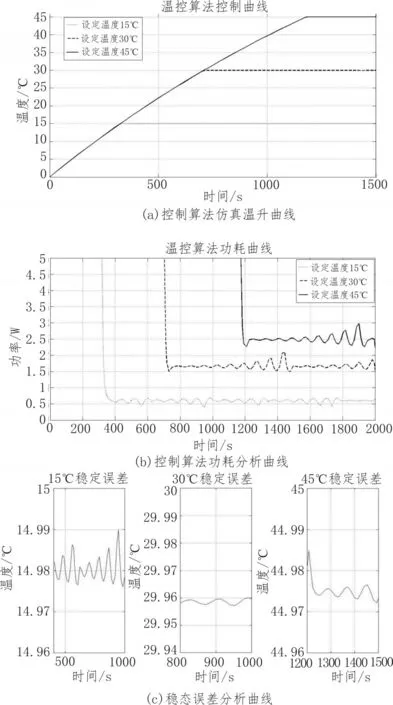
图9 控制算法仿真曲线

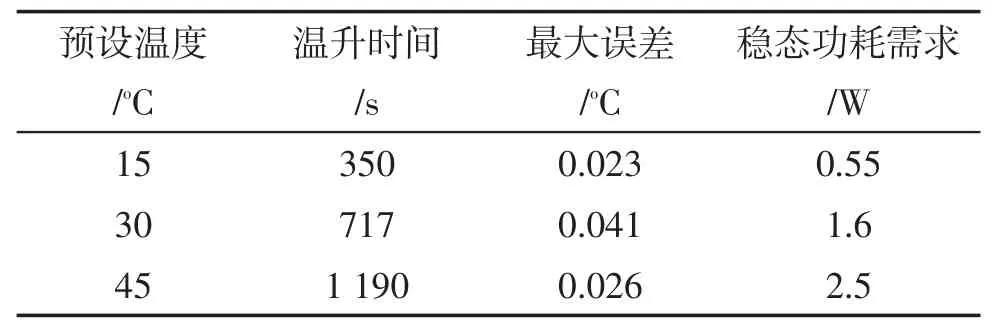
表1 仿真结果指标

[1]丁松鹤.基于CPT效应的高精度磁场探测实验研究[D].北京：空间科学学报，2013.

[2]钱江.光泵原子磁力仪及其应用[J].光学与光电技术，2015，13（3）:93-97.

[3]刘国宾，孙献平，顾思洪，等.高灵敏度原子磁力计研究进展[J].物理，2012，41（12）:803-810.

[4]李曙光，周翔，曹晓超.全光学高灵敏度铷原子磁力仪的研究[J].物理学报，2010，59（2）:882.

[5]吴国龙.微结构磁传感器无磁加热控温技术研究[D].哈尔滨：哈尔滨工程大学，2014.

[6]Dang H B，Maloof A C，Romalis M V.Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer[J].Applied Physics Letters，2010，97（15）:151110-151110-3.

[7]Spek A V D，Mulders J，Steenhuysen L.Vapor pressure of rubidium between 250 and 298 K determined by combined fluorescence and absorption measurements[J].Journal of the Optical Society of America B，1988，5（7）:1478-1483.

[8] Knappe S， Kitching J， Hollberg L， et al.Temperature dependence of coherent population trapping resonances[J].Applied Physics B，2002，74（3）:217-222.

[9]张丽芝.影响CPT磁共振信号的参量分析[D].浙江：浙江大学，2012.

[10]晋芳，杨宇山，郑振宇，等.原子磁力仪研究进展[J].地球物理学进展，2011，26（3）:1131-1136.

[11]DS SolidWorks公司.SolidWorks Simulation高级教程[M].浙江：机械工业出版社，2011

[12]周基，芮勇勤，谭勇.基于Solidworks建模技术的工程有限元仿真分析[J].中外公路，2010，30（6）:194-196.

[13]杨世铭.传热学[M]北京：高等教育出版社，2010

[14]王栋.高精度陀螺温控系统的工程实现研究[D].黑龙江：哈尔滨工程大学，2006.

[15]马小霞.陀螺仪数字温度控制系统研究[D].北京：中国航天第二研究院航天科工集团第二研究院，2004.

[16]李科.温控系统的智能PID控制算法研究[D].湖北：华中科技大学，2006.

[17]杨益兴，崔大连，周爱军.模糊自适应PID控制器及Simulink仿真实现[J].舰船电子工程，2010，30（4）:127-130.