基于改进遗传算法的水库群水沙联合优化调度模型应用研究

赵 磊，李泊溪

(辽宁天阳工程技术咨询服务有限公司，辽宁 沈阳 1100001)

水库水沙联合优化调度对于水库调节十分重要，即保证水库的兴利和防汛功能，又调节水库泥沙淤积，增大水库的调节库容，为此许多学者采用不同优化方法对水库水沙联合调度进行优化计算，其中传统遗传算法采用随机概率数学方法对目标进行优化，可实现多目标优化，在水库水沙联合调度中得到较大程度的应用。但是传统遗传算法收敛局限，为此有学者结合最小生境理论对传统遗传算法的目标值进行自适应度的调整，并在一些水库优化调度中得到应用，但在水库水沙联合优化调度中应用还较少，而辽宁中部位于辽宁生平原区域，风沙较大，该区域梯级泥沙淤积量相比较大。为此本文引入改进的遗传算法，对该区域水库群水沙进行联合优化调度研究。

1 改进遗传算法计算原理

改进的遗传算法采用自适应因子进行变量交叉概率优化求解，各交叉概率的变量求解方程为:

PC=PC1-(PC1-PC1)(fmax-f′)

(1)

式中，PC1—变量交叉概率最大值；fmax—目标函数的自动适应最大值；f′—变量自适应值。改进的遗传算法在交叉变量概率计算的基础上，对变量变异概率进行计算，计算方程为：

Pm=(Pm1-Pm2)(fmax-f′)

(2)

式中，pm1—变量变异最大概率；pm2—变量变异最小概率。改进的遗传算法采用最小生境方法对样本个体进行自适应度的优化，计算方程为：

(3)

式中，dij—样本个体间距；Si—各个样本变量个体的最小生境总和。其中dij的计算方程如下：

(4)

式中，Xi—变量种群i个体数；Xj—变量种群j个体数。经过自适应调整后目标函数计算值为：

f′(Xi)=f(Xi)/Si

(5)

式中，f(Xi)—调整前的目标适应优化值；f′(Xi)—调整后的目标适应优化值。改进的遗传算法结合Holt- Winters对模型进行时间步长的优化计算，计算方程为：

Yt+s=(Yt+GtS)Ht-L+S

(6)

式中，Yt+s—步长S下的目标平滑值；S—调整的时间步长；Ht—季节调整系数；Gt—趋势分析值。改进遗传算法结合适应因子对个体的适应度进行调整分析，适应度的计算方程为：

(7)

式中，M—样本集合数量，本文为水库个数；f—目标函数值，本文为水库群水沙联合调度优化值；Qi—输出变量值。

2 水库群水沙联合调度研究

2.1 水库群水沙调度概况

本文以辽宁中部某4座梯级水库为研究对象，各水库的主要特征参数见表1。结合各水库的水沙联合调度规则，以水沙联合调度为主要目标，结合改进的遗传算法对4座梯级水库下的水沙进行联合优化调度研究。

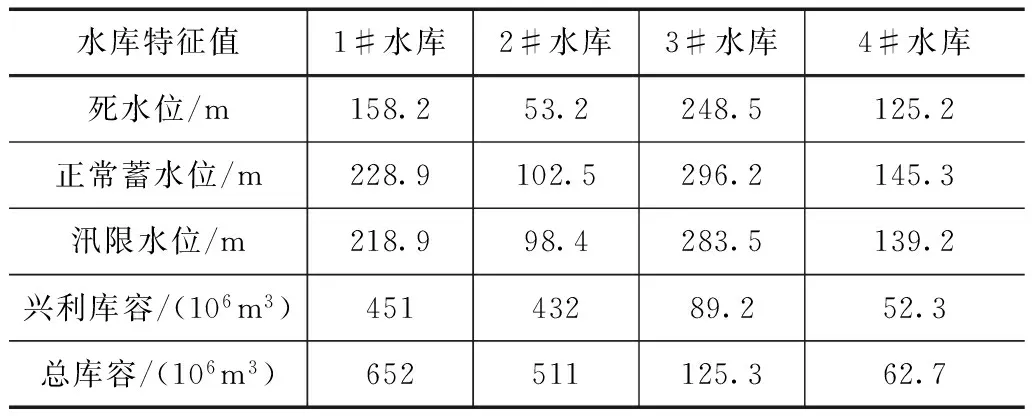
表1 梯级水库主要特征值

2.2 不同调度方案下各水库水沙联调优化求解

为对比不同算法对水库水沙联合调度求解的影响，结合改进前后的遗传算法求解不同调度方案下的水库兴利水量和泥沙淤积量进行优化求解，优化对比结果见表2和图1。

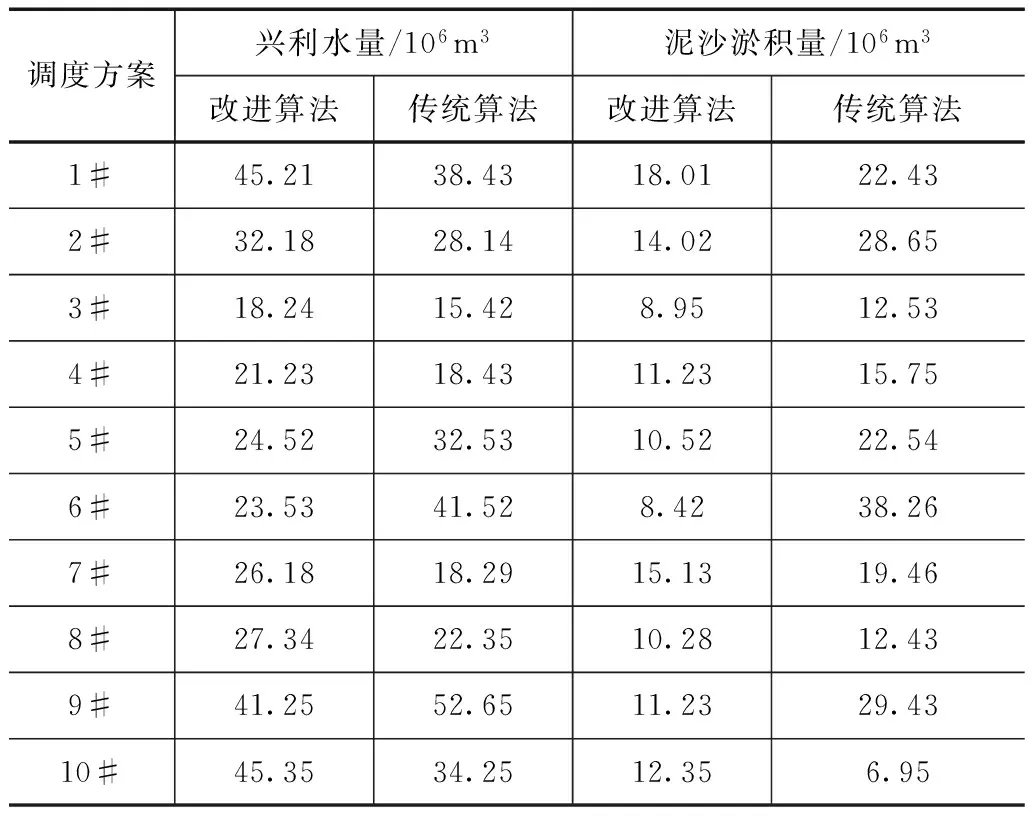
表2 不同调度方案下的水库水沙联调优化结果

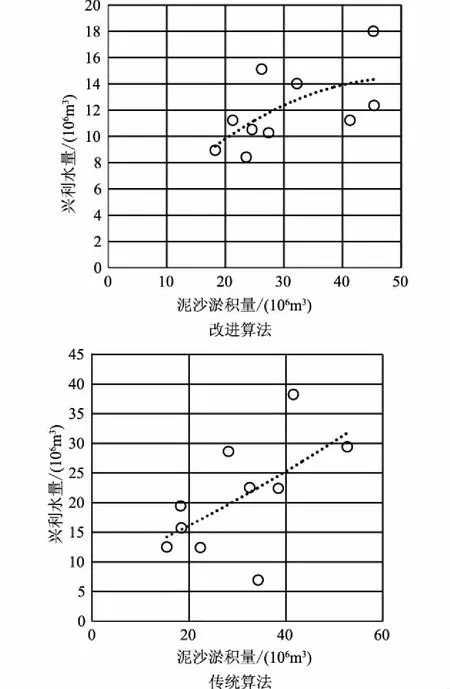
图1 不同算法下各调度方案下水沙相关分析图

从表2中看出，相比于传统遗传算法，改进遗传算法下水库水沙联合调度结果好于传统遗传算法，从各调度方案下的水沙联合调度结果可以看出，相比于传统算法，不同水库调度方案下水库联合优化的兴利水量均值提高25.3%，泥沙淤积调整量减少43.8%，优化效果提高较为明显。这主要是因为改进遗传算法对目标值进行不断调整寻优，对目标优化结果好于传统算法。从图1中可看出，改进算法下的水沙关系较好，呈现指数相关变化，而传统算法下水沙相关较弱。

2.3 水库联调方案下的水沙调度优化结果

结合改进遗传算法对各水库不同调度方案下的水沙联调进行优化计算，优化调度分析计算结果见表3和图2。

从表3中看出，在各调度方案下，9#调度方案下的水库群水沙联合调度达到最优结果，9#调度方案的调度原则为丰水期尽量抬高各水库水位起调值，枯水期尽量降低兴利起调水位，该调度方案下的水库群水沙联合调度将达到最优结果。2#调度方案下水库水沙联合调度在各方案下效果最差，这主要是因为该调度方案未能有效的对水库的兴利库容进行有效调节和利用，使得该方案下水库水沙联合调度效果较低。从图2中看出，采用改进遗传算法下各水库的水沙联合调度线都较为光滑，且兴利水量大于泥沙淤积量，优化调节效果较为明显，各水库水沙联合调度线可为各级水库制定最优的调度方案。

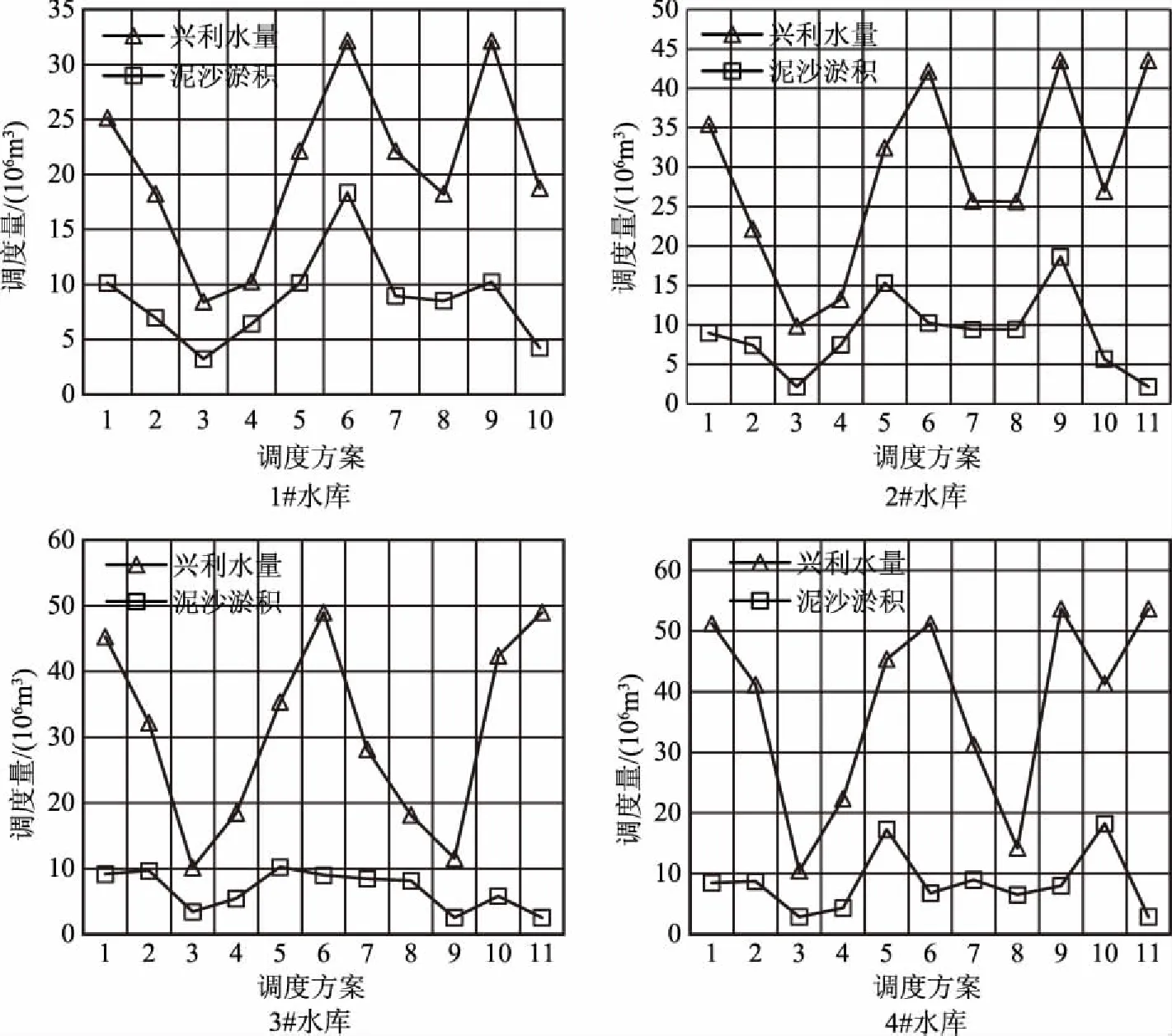
图2 不同调度方案下的水库联合调度线过程

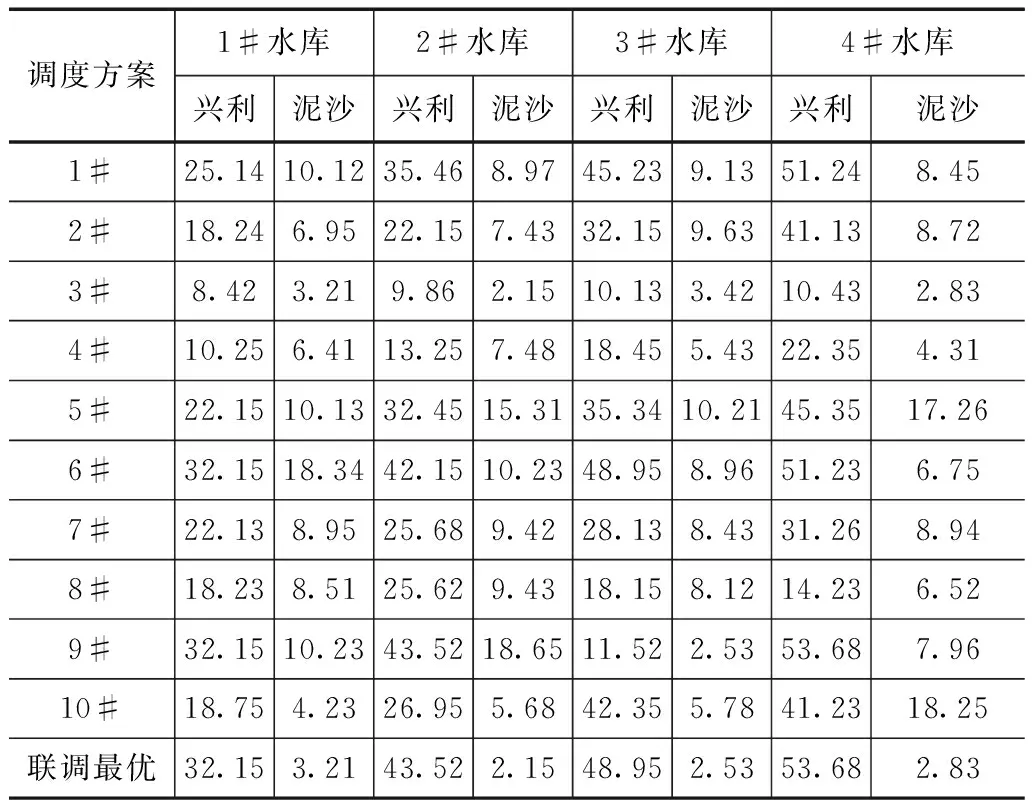
表3 水库联调方案下的水沙调度优化结果 单位：106m3

3 结论

本文采用改进的遗传算法对辽宁中部梯级水库群的水沙进行联合优化调度研究，结论如下：

(1)改进遗传算法对梯级水库群水沙联合优化调度效果明显，适用于梯级或单一水库的水沙联合优化调度计算。

(2)基于改进遗传算法的水库群水沙联合优化调度模型可分析不同调度方案下的兴利水量和泥沙淤积量，并分析出最优的调度方案，为水库多目标优化调度提供较好的技术支撑。

[1] 刘文亮. 基于遗传蚁群混合算法的水库优化调度研究[D]. 太原理工大学, 2008.

[2] 俞琨. 青草沙水库调度运行中的控沙措施研究[J]. 水利规划与设计, 2013(12): 30- 32.

[3] 向波, 纪昌明, 罗庆松. 免疫粒子群算法及其在水库优化调度中的应用[J]. 河海大学学报(自然科学版), 2008(02): 198- 202.

[4] 贾瑞红. 单一水库优化调度方案在水库调度中的应用研究[J]. 水利规划与设计, 2013(11): 23- 25.

[5] 朱余生. 基于分时电价的水电站水库优化调度研究[D]. 河海大学, 2007.

[6] 刘伟, 刘明丽. 莲花水库优化调度研究[J]. 水利技术监督, 2004(05): 43- 47.

[7] 彭帅英, 李广杰, 彭文, 等. 基于改进遗传算法的Holt- Winters模型在采空沉陷预测中的应用[J]. 吉林大学学报(地球科学版), 2013(02): 515- 520.

[8] 张杰, 冯民权, 王钰. 基于改进遗传算法的水库群水质水量优化调度研究[J]. 中国农村水利水电, 2017(02): 60- 64.

[9] 陈端, 陈求稳, 陈进. 基于改进遗传算法的生态友好型水库调度[J]. 长江科学院院报, 2012(03): 1- 6+12.

[10] 畅建霞, 黄强, 王义民. 基于改进遗传算法的水电站水库优化调度[J]. 水力发电学报, 2001(03): 85- 90.