基于并行预处理算法的三维重力快速反演

王泰马国庆，李 野，林 松

1.吉林大学地球探测科学与技术学院，长春 130026 2.吉林省电力勘测设计院，长春 130021

0 引言

多年来，重力勘探被广泛地应用于大地构造、勘探矿产和油气源，以及工程与环境调查等研究领域[1-3]。在重力勘探研究中，三维重力反演已经成为一种重要和有效的处理和解释手段。通常情况下，重力数据的三维反演往往是病态的，即需要一些先验信息或约束条件来保证解的唯一性和准确性。基于正则化方法，地球物理学家们做了很多工作来解决反演的不稳定性和非唯一性问题。Li等[4-5]采用目标函数的深度权函数进行磁化率反演和密度反演, 通过赋予随深度增加的棱柱体单元更多的权重来抵消核函数的固有衰减(即“趋肤效应”)。随着重力数据采集量和精度的提高[6-8]，快速处理大规模高精度数据在处理与解释方面越来越常见。解决大规模三维重力数据反演计算问题面临两个困难：需要足够的计算机内存来储存反演过程中生成的矩阵；减少反演求解过程中矩阵向量乘法的计算用时。对于这样的问题，特别是在航空测量成千上万个数据点的情况下，寻求一种快速、有效的算法对于快速解决三维反演问题十分重要。

共轭梯度算法(conjugate gradient algorithm, CG)是一种解决大型线性重力反演的通用迭代算法。对其使用有效的预处理因子，预处理共轭梯度算法(PCG)已经在很多领域研究[9-12]中证明了其良好的性能和应用效果。然而，不同的预处理因子在提高反演速率和减少迭代次数方面的能力有所不同。在迭代过程中，准备(分解)预处理因子也需要额外的计算时间。因此，反演计算效率由迭代次数和总计算时间综合决定。随着图形处理单元(GPU)的计算能力和可编译能力的不断增强，利用GPU辅助进行科学计算逐渐成为研究的热点。CUDA[13](统一计算设备架构)是显卡厂商NVIDIA推出的硬件和软件架构平台，使GPU成为一种并行计算工具，解决复杂的计算问题，而不只是完成当初的图像渲染。如今，CUDA已经成为最适合并行计算的手段之一：Moorkamp[14]等使用CUDA进行了标量和张量数据的正演并行计算；Chen等[15]利用CUDA对重力及梯度数据进行了三维相关成像的并行计算；Liu等[16]提出了CUDA下基于概率成像的三维磁化率反演。

本文为提高三维重力数据反演效率，基于CPU和GPU给出一种并行的预处理共轭梯度算法。首先简单地介绍三维重力数据正反演的原理，给出本文的并行算法的流程；进而通过不同网格大小的单一模型试验比较出CPU/GPU算法相对于串行CPU算法的加速能力，以及用组合模型试验比较基于两种不同预处理算子的并行预处理共轭梯度算法与传统共轭梯度算法在重力反演中的效果和加速能力；最后，将该算法应用于美国路易斯安那州Vinton盐丘实测重力数据三维反演中，进一步证明本文并行预处理快速方法的高效性和适用性。

1 方法原理

1.1 重力数据正反演理论

根据牛顿万有引力定律，三维重力数据的正演是计算由地下密度分布为ρ引起的在地表观测的重力异常g。为简单起见，将三维地下空间划分为有限多的密度一定的长方体单元来计算重力数据。在笛卡尔坐标系中，我们定义x轴和y轴为水平方向，z轴为垂直向下，其分别代表东向、北向和深度方向。根据Haz[17]提出的积分解，由密度为ρ的单一棱柱体单元C在观测点O=(x0,y0,z0)处产生的重力异常为

(1)

(2)

考虑到有n个观测点和m个长方体模型单元，其线性关系也可以用矩阵形式表示为

gn×1=Gn×mρm×1。

(3)

式中：g是地表观测重力异常值；ρ是地下空间密度分布；G是重力正演核函数。

在三维重力反演中，地下网格个数远大于地面观测点的个数，也就是说，反演问题是欠定的，需要引入正则化约束来解决反演过程的非唯一性和不确定性[18]，恢复出大多数合理的解。我们用正则化约束Tikhnov参数方程P(ρ)为

Pα(ρ)=φ(ρ)+αs(ρ)=

(4)

式中：Wd是数据误差加权矩阵；Wz是深度加权矩阵形式，计算公式为Wz=(z+z0)-1/2，用于抵消核函数矩阵G随深度的固有衰减，克服趋肤效应，z是长方体单元平均埋深，z0取决于模型离散化的块体大小和重力数据观测高度；s(ρ)是稳定函数；φ(ρ)是观测数据与预测数据的拟合函数，为正则化参数。φ(ρ)值对反演结果有很大影响，本文选取一种自适应方法选择正则化参数，即随着反演结果的收敛逐渐减小稳定函数的贡献值。初次迭代计算得到的正则化参数表达式为

(5)

随后的迭代计算中，通过

(6)

计算正则化参数的值。

根据Pilkington[10]研究，式(4)又可以被转换成矩阵形式：

⟺AM=b，

(7)

ATAM=ATb。

(8)

1.2 共轭梯度算法和预处理策略

共轭梯度算法是一种求解线性方程组的快速迭代算法，其收敛速度比最速下降法和牛顿法下降法要快。CG算法只进行矩阵向量乘积和向量内积运算，需要低存储和低计算成本，被广泛地应用于地球物理及其他领域反演中。重力反演的基本CG算法为

fork=0;m0=0 andr0=AT(b-Am0)

whiler0≠0

k=k+1,

ifk=1,

p1=r0

pk=rk-1+βkpk-1,

end

qk=Apk,

mk=mk-1+akpk,

rk=rk-1-akATqk,

end

(9)

式中；k为迭代次数，rk为目标函数的梯度；pk和αk分别表示迭代的搜索方向和步长；βk和qk是迭代计算的中间变量。在算法中可以发现，系数矩阵A的逆矩阵不需要被计算。这对于大规模数据可以节省很长时间和很大存储空间。随着观测数据量增多或者离散网格数加大的三维实际反演问题，矩阵A也变得相当大。因此，反演的迭代次数和计算时间应该被考虑到。众所周知，CG算法收敛速度的快慢受系数矩阵特征值分布控制。为了减少迭代次数进而加快收敛速度，国内外许多研究人员将式(8)变换为式(10)，使特征值分布尽量集中在对角线上。这种改善特征值分布的方法叫做预处理方法，应用于CG算法可得到预处理共轭梯度法(PCG),算法如式(11)。

PATAM=PATb。

(10)

fork=0;m0=0 andr0=AT(b-Am0)

whiler0≠0

zk=Pr

k=k+1,

ifk=1,

p1=z0

pk=zk-1+βkpk-1,

end

qk=Apk,

mk=mk-1+akpk,

rk=rk-1-akATqk,

end

(11)

其中，P是为提高收敛速度的预处理算子。

可以看出，相比于CG算法(9)，PCG算法(11)只是多了一步zk=Pr，若P为单位矩阵，则PCG算法退化为CG。理想情况下，P是(ATA)-1的近似，这样PATA近似等于单位矩阵。为了加速CG算法的收敛速度，PATA特征值分布必须比原对称正定矩阵ATA更加集中，改善了方程的条件数，会提高迭代速度。因此，如何选取一个有效的预处理因子对于减少反演迭代次数是非常重要的。PCG方法在很多研究中已经证明其效率和良好的性能。本文选取两种不同的预处理算子应用于三维重力反演。

一种最常见和简单的方法是对角预处理算子(DP)。这种方法是使算子P等于重力反演中第一次迭代的最小二乘解，在对角预处理共轭梯度算法中，选取P等于ATA的对角元素，即P=diag(diag(ATA))。

另一种预处理算子可以从系数矩阵直接近似推导，为对称逐次超松弛(SSOR)预处理方法。SSOR预处理方法相比于对角预处理方法包含了更多的系数矩阵(地球物理信息)的信息。其分解方式是将矩阵ATA分解为

ATA=D-LAA-LAAT，

(12)

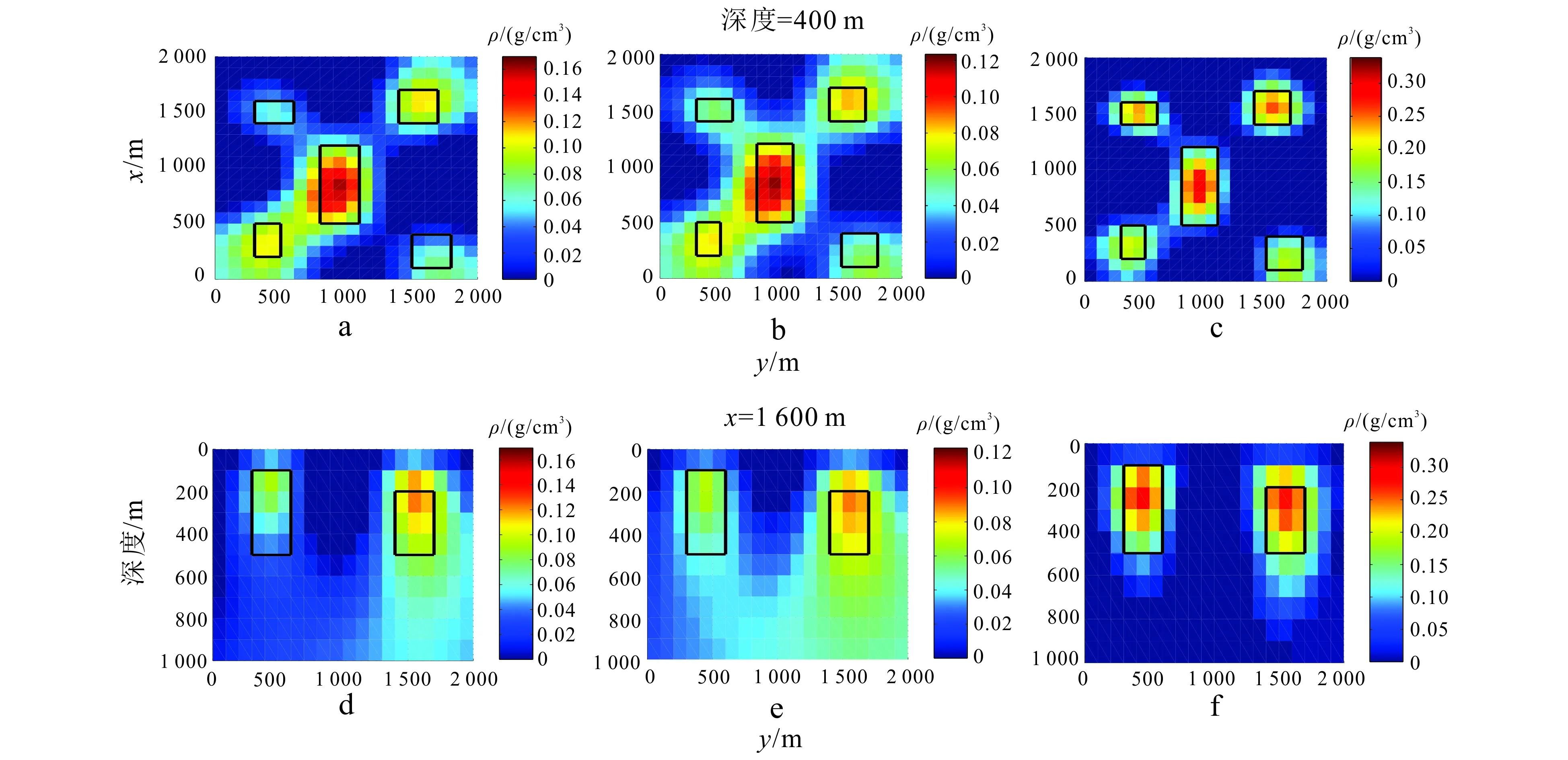
其中；D是系数矩阵；ATA对角元素组成的对角矩阵；LAA是ATA的下三角矩阵。w(0

(13)

虽然预处理共轭梯度法能够从减少迭代次数的方面提高反演收敛速度，但是每一次迭代过程中构建(分解)预处理算子需要花费很多时间，尤其是处理大数据量的三维反演。笔者尝试通过改进并行算法来进行三维快速反演。

1.3 并行算法的设计

近些年来，可编译的NVIDIA GPU已经被开发用于高性能计算，这吸引了研究人员和开发者更多的关注。当处理大量地球物理数据时，拥有流多处理器集群的GPU具有极高的计算速度。在解决耗时问题的需求下，GPU已经成功应用于许多地球物理并行计算研究中。统一计算设备架构(CUDA)是一种使用NVIDIA GPU作为数据并行计算设备的硬件和软件架构。CUDA技术最初只支持C++语言，需要高水平的编程。随着GPU计算能力的提高，MATLAB在版本R2010b[19]后，提供并行计算工具箱(PCT)使用户进行快速并行计算更加方便。MATLAB中强大的GPU计算能力是在Tesla和Quadro GPU计算产品上开发的，需要使用最新的支持CUDA的NVIDIA显卡，例如NVIDIA Tesla 10系列或20系列产品，支持计算能力在1.3或更高的计算能力。本文算法的设计平台是MATLAB，用来讨论CPU和GPU算法加速问题。

将上节提到的共轭梯度算法用串行程序分步计时后，发现每一步迭代过程中的更新矩阵r0、qk、rk是最耗时的部分。在CG算法的重力反演中主要耗时问题被归纳为矩阵向量乘积运算和大系数矩阵A的内积运算。因此，我们将这部分用GPU计算，其他部分仍用CPU作常规的串行计算。为了体现GPU的加速能力和适用性，笔者先利用不同网格大小的单一模型进行三维重力共轭梯度反演，通过记录1 000次迭代的时间来比较CPU串行与CPU/GPU并行算法计算速度，比较结果见图1。显然CPU/GPU算法计算能提高计算效率，尤其是针对大数据量的重力数据反演。通过曲线可以看到，在没有预处理算子的CG反演中，并行算法相比串行程序加快了大约4.5倍。本文程序运行的硬件配置如下：

图1 三维重力共轭梯度反演的CPU和CPU/GPU计算时间对比图Fig.1 CPU and CPU/GPU computing time for the CG algorithm in 3D gravity inversion

CPU Intel Xeon E5-2620 6-core 2.0 GHz, 7.2 GT/s

GPU NVIDIA Tesla C2050

上节我们提到应用不同预处理算子在预处理共轭梯度反演中可以减少迭代次数，在某种程度上使反演收敛快，减少耗时。然而，随着数据量和网格数增大，构建预处理算子需要更多额外的时间应该被考虑。因此，本文给出GPU加速的PCG并行算法进行三维重力数据反演，在减少迭代次数的同时，进一步解决耗时问题。并行的PCG算法流程(图2)为：1)初始化MATLAB环境；2)读入观测重力数据，开始计时；3)并行计算模型权Wm和深度权Wz，后用gather()函数将结果返回至CPU；4)初始化m0，计算A,b；5)用gpuArray()函数将以上数据传输到GPU，开始迭代，预处理因子P、搜索方向pk和搜索步长αk用GPU计算，其余都在CPU串行计算；6)达到迭代终止条件，停止计时，返回密度结果m到CPU，绘图。其中gpuArray()和gather()函数是由Parallel Computing Toolbox(PCT)工具箱提供的负责CPU和GPU之间数据收集和传输的函数。

图2 重力反演的并行PCG算法流程图Fig.2 Flowchart of the parallel PCG algorithm in gravity inversion

2 模型实验

为了比较并行预处理共轭梯度算法在三维重力数据反演的加速能力，我们首先模拟一个由5个长方体组成的复杂模型。各个模型参数如表1给出。三维地下空间被离散成20×20×10个小棱柱体单元，其单元大小为100 m×100 m×100 m(x×y×z)。图3a展示了不同大小和密度的模型体的空间分布。对模型数据加入最大值5%的高斯噪声，模拟真实数据，以验证算法的抗噪性，这样地面观测的含噪剩余重力异常如图3b所示。

表1 组合模型参数表

我们将前面介绍的两种不同的预处理方法应用于模型数据的三维重力反演，比较其并行程序与CPU串行的CG算法的计算时间和结果，来验证并行预处理共轭梯度反演的高效性和有效性。3种方法重力反演结果如图4。图4a、b、c是反演结果在深度为400 m的水平切面图，图4d、e、f是在水平x方向为1 600 m的垂直切面图。黑色矩形框为每个模型的真实位置。可以发现：对角预处理共轭梯度算法(DPCG)的反演结果与传统的CG算法较为接近；而对称逐次超松弛预处理共轭梯度算法(SSOR-PCG)反演出的密度值与真实密度值更为接近，图像更为紧致，空间上更接近真实模型位置。

在计算速度上，我们选取Pilkington[10]在1997年提出的残差记录方式，通过下降曲线的比较来反映不同算法在三维重力反演中收敛的快慢。本文对所有算法选择计算500次迭代，统计公式为:R= (g-Gρ)T(g-Gρ)/N，记录的曲线如图5。与传统的CG算法相比，PCG算法残差曲线明显下降较快，表明其用较少的迭代次数即可达到相同的残差。由图5可以看到，迭代500次后，传统的CG算法和并行的DCPG算法最小残差能达到0.275，并行的SSOR-PCG算法能达到0.013。如同图中黑色直线截取指示，当反演达到同一残差(0.04)的时候，SSOR-PCG算法只需要12次迭代计算，而DPCG算法和传统CG算法分别需要46和100次迭代计算。由于系数矩阵A的变化，每次迭代计算中分解预处理矩阵也需要额外不可忽略的计算时间，因此计算效率需由迭代时间和总计算用时共同决定。表2给出了3个算法的计算用时及加速比。对于网格大小为20×20×10的三维重力反演计算，选取500次迭代时，并行的PCG算法相比串行的CG算法只有2.2倍。然而实际上迭代终止于同一迭代残差(0.04)时候，相比于CG算法，并行DPCG可以达到4.7倍加速比，并行SSOR-PCG算法能获得18.7倍的加速比。综上，并行的SSOR-PCG预处理方法在三维重力数据反演中效果最好，反演出的密度更接近真实密度，模型更加紧致，在计算速度上可比传统串行的CG算法获得高达18.7倍的加速比，减少了计算耗时，提高了三维密度反演效率。

图3 组合模型的空间分布图(a)和含噪剩余重力异常(b)Fig.3 Three-dimensional distribution of synthetic model (a) and residual noise-contaminated gravity anomaly (b)

a,d为传统共轭梯度算法；b,e为对角预处理共轭梯度算法；c,f为SSOR预处理共轭梯度算法。图4 3种算法反演结果的深度切片和垂直切片Fig.4 Depth slices and vertical slices of results obtained by three inverse algorithms

黑色水平线表示同一迭代残差下的迭代次数。图5 组合模型数据反演迭代残差Fig.5 Residual error curve for the synthetic gravity anomaly inversion

Table2ComparisonoftheruntimeandspeedupofCGandparallelPCG

方法500次迭代时间/s反演结果需要迭代次数运行时间/s加速比CG⁃CPU543100108．61．0倍DPCG⁃GPU2504623．04．7倍SSOR⁃PCG⁃GPU242125．818．7倍

3 实际数据

为了进一步验证本文方法对实测数据的有效性，我们将表现效果最好的并行SSOR-PCG算法应用于美国路易斯安那州西南部Vindon盐丘实测地面重力数据，通过快速反演来恢复地下密度分布。许多学者对该地区进行了研究[20-22]，其大部分结果表明该盐丘的异常主要是由岩盖引起，其平均剩余密度为0.55 g/cm3，深度范围为200～600 m。对原始数据去除背景场后，在研究区域中心截取3 000 m×3 000 m 的区域，反演区域被离散成20×20×20=8 000个小长方体，每个长方体的大小为150 m×150 m×50 m。图6a给出了处理后的Vindon盐丘的剩余布格重力异常。根据Ennen[23]在2011年的研究表明，岩盖的密度为2.75 g/cm3，周围围岩(主要是页岩和砂岩)密度为2.20 g/cm3，据此我们给出密度约束上下限为0.00～0.55 g/cm3。图6b给出三维快速反演结果在深度为250 m的切片，其良好地指示出异常的东西向范围约为1 300 m，南北向范围约为900 m。图6c给出反演结果在东西和南北向的垂直交叉剖面，在空间上可以清晰地展示出异常的范围，深度范围为150～600 m。图7为Marfurt等[24]在Vinton盐丘地区通过垂直地震剖面(VSP)成像得到的二维垂直地震剖面以及经时间深度转换得到的解释层位，将反演结果与地震层位资料对比，可以看到高密度体的深度范围与地震层位解释中岩盖的埋深相吻合，进一步验证了本文方法的可靠性。在计算速度上，应用并行的SSOR-PCG算法进行三维重力快速反演达到这一结果用22次迭代，只需75.6 s。综上，实测数据的反演结果也证实了本文并行的预处理方法可以应用于三维重力快速反演，提高了计算效率。

a.Vinton盐丘的异常重力数据；b.快速反演结果在深度为250 m的切片；c.通过异常体中心的垂直交叉剖面，东向为1 650 m，北向为1 050 m。图6 Vinton盐丘重力异常及反演结果图Fig.6 Gravity anomaly and inversion results of Vinton Salt dome

剖面(左)；层位解释(右)。图7 地震测量及层位解释结果Fig.7 Result of seimic horizon interpretaion and measurement

4 结论

1) 本文将一种并行的预处理共轭梯度算法应用于三维重力数据的光滑反演，来快速获得地下密度分布。并行的PCG算法与传统的CG算法相比，在减少迭代次数的同时缩短了计算总用时，提高了三维密度反演的效率。

2)含噪组合模型测试结果表明：对称逐次超松弛预处理算子效果较好，反演结果更加紧致并贴近实际模型的三维密度分布。计算效率是由较少的迭代次数和总计算时间共同评价的。实验表明与2.0 GHz CPU上传统CG算法的串行代码相比，本文基于NVIDIA Tesla C2050 GPU并行的SSOR-PCG算法收敛更快，获得约19倍的加速比。说明该方法既能加快反演收敛速度，又能提高反演精度。

3)通过美国Vinton盐丘实测重力数据的三维重力快速反演计算，得到的反演结果深度与地震层位反演结果吻合，并有着较高的效率，验证了该方法在实际数据三维快速密度反演应用方面的高效性和有效性。

[1] 刘财, 杨宝俊, 冯晅,等. 论油气资源的多元勘探[J]. 吉林大学学报(地球科学版), 2016，46(4):1208-1220.

Liu Cai, Yang Baojun, Feng Xuan, et al. Multivariate Exploration Technology of Hydrocarbon Resources[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(4):1208-1220.

[2] Nettleton L L. Gravity and Magnetics in Oil Prospe-cting[M]. New York：McGraw-Hill Companies, 1976.

[3] Hinze W J. The Role of Gravity and Magnetic Methods in Engineering and Environmental Studies[J]. Geotechnical and Environmental Geophysics, 1990, 1:75-126.

[4] Li Y, Oldenburg D W. 3-D Inversion of Magnetic Data[J]. Geophysics, 1996, 61(2):394-408.

[5] Li Y, Oldenburg D W. 3-D Inversion of Gravity Data[J]. Geophysics, 1998, 63(1):109-119.

[6]Bell R E, Anderson R, Pratson L. Gravity Gradio-metry Resurfaces[J]. Leading Edge, 1997, 16(1):55-59.

[7] Lee J B. FALCON Gravity Gradiometer Technology[J]. Exploration Geophysics, 2001, 32(4):247-250.

[8] 黄大年, 于平, 底青云,等. 地球深部探测关键技术装备研发现状及趋势[J]. 吉林大学学报(地球科学版), 2012, 42(5):1485-1496.

Huang Danian, Yu Ping, Di Qingyun, et al. Development of Key Instruments and Technologies of Deep Exploration Today and Tomorrow[J]. Journal of Jilin University(Earth Science Edition), 2012,42(5): 1485-1496.

[9] Canning F X, Scholl J F. Diagonal Preconditioners for the EFIE Using a Wavelet Basis[J]. IEEE Transactions on Antennas & Propagation, 1996, 44(9):1239-1246.

[10] Pilkington M. 3D Magnetic Imaging Using Conjugate Gradients[J]. Geophysics, 1997, 62(4):1132-1142.

[11] Chen R S, Yung E K N, Chan C H, et al. App-lication of Preconditioned CG-FFT Technique to Method of Lines for Analysis of the Infinite-Plane Metallic Grating[J]. Microwave & Optical Technology Letters, 2000, 24(3):170-175.

[12] Chen R S, Yung K N, Chan C H, et al. Application of the SSOR Preconditioned CG Algorithm to the Vector FEM for 3D Full-Wave Analysis of Electromagnetic-Field Boundary-Value Problems[J]. IEEE Transactions on Microwave Theory & Techniques, 2002, 50(4):1165-1172.

[13] NVIDIA Corporation. NVIDIA CUDA Programming Guide[R]. Santa Clara CA: NVIDIA Corporation, 2008.

[14] Moorkamp M, Jegen M, Roberts A, et al. Massively Parallel Forward Modeling of Scalar and Tensor Gravimetry Data[J]. Computers & Geosciences, 2010, 36(5):680-686.

[15] Chen Z, Meng X, Guo L, et al. GICUDA: A Parallel Program for 3D Correlation Imaging of Large Scale Gravity and Gravity Gradiometry Data on Graphics Processing Units with CUDA[J]. Computers & Geosciences, 2012, 46(3):119-128.

[16]Liu G, Meng X, Chen Z. 3D Magnetic Inversion Based on Probability Tomography and Its GPU Implement[J]. Computers & Geosciences, 2012, 48(9):86-92.

[18] Zhdanov M S. GeophysicalInverse Theory and Re-gularization Problems[M].Salt Lake: Elsevier Science, 2002:51-57.

[19]Szymczyk M, Szymczyk P. Matlab and Parallel Computing[J]. Image Processing & Communications, 2014, 17(4):207-216.

[20] Oliveira V C Jr, Barbosa V C F. 3-D Radial Gravity Gradient Inversion[J]. Geophysical Journal International, 2013, 195(2):883-902.

[21] Geng M, Huang D, Yang Q, et al. 3D Inversion of Airborne Gravity-Gradiometry Data Using Cokriging[J]. Geophysics, 2014, 79(4):G37-G47.

[22] Wang T H, Huang D N, Ma G Q, et al. Improved Preconditioned Conjugate Gradient Algorithm and Application in 3D Inversion of Gravity-Gradiometry Data[J]. Applied Geophysics,2017, 14(2): 301-313.

[23]Ennen C. Structural Mapping of the Vinton Salt Dome, Louisiana, Using Gravity Gradiometry Data[J]. Seg Technical Program Expanded Abstracts, 2011, 30(1):830-835.

[24] Marfurt K J, Zhou H W, Sullivan E C. Development and Calibration of New 3-D Vector Vsp Imaging Technology: Vinton Salt Dome, LA[R]. Houston:University of Houston, 2004.