改进的多目标量子遗传算法在南水北调东线工程江苏段水资源优化调度中的应用

方国华，郭玉雪，闻 昕，黄显峰

(河海大学水利水电学院，江苏 南京 210098)

跨流域调水作为调节区域水资源时空分布不均、实现水资源合理配置的重要手段，正逐渐被广大水利工作者和各国政府决策者关注与重视。南水北调东线工程江苏段是我国重大跨流域调水工程之一。工程沿线有洪泽湖、骆马湖、南四湖下级湖等调蓄湖泊，构成了总调节库容达45.25亿m3的沿线水量调节系统；从长江至南四湖下级湖可分为3个大段，每段设3级提水泵站，共计9个提水梯级。这些调蓄湖泊和各级泵站，使南水北调东线水资源系统具有较大的调蓄能力，一方面能统筹调配江水、淮水及沂沭泗水，实现系统内水资源的互济互调；另一方面能形成沿输水线路的水量调节系统，具有实现预调水、合理利用洪水资源、保障峰量供水等多种实际用途[1]。因此，研究南水北调东线工程江苏段水资源优化调度，提高工程的运行管理水平，是十分必要和紧迫的。

在研究南水北调东线工程江苏段的优化调度问题时，学者们主要从系统的概化方式、优化目标的选择以及模型的求解方法3个方面入手进行分析和改进。2012年，侍翰生等[2]在对南水北调东线工程江苏段进行分析概化的基础上，采用基于动态规划与模拟退火相结合的混合算法对江苏受水区水资源调度方案进行了优化，模型运算结果良好且优于系统常规调度结果；2015年，王文杰等[3]在对南水北调东线工程水资源系统概化的基础上，建立江苏段水量优化调度数学模型，模拟计算了3种不同保证率工况下的水量调配方案；2016年，王攀等[4]提出了一种改进的量子遗传算法，并以南水北调东线工程江苏段水资源优化调度为例，确定湖泊群优化调度方案。之后，开始有学者针对南水北调东线工程江苏段考虑多目标并行结合多目标属性决策的优化调度研究，2016年，于凤存等[1]构建了缺水量最小与系统总抽水量最小的多目标优化调度模型，并利用NSGA-Ⅱ算法进行求解，采用基于组合权重的多属性决策方法对非劣方案集进行评价，得到南水北调东线工程江苏段湖泊群系统的最优水量调配方案；2017年，闻昕等[5]构建了以系统缺水量和抽江水量为目标的联合优化调度模型，研发基于改进的多目标粒子群算法的模型求解方法，建立组合赋权-TOPISIS方法进行多属性决策，提出了以大型泵站工程为核心的骨干枢纽联合调度方案。

随着系统分析理论的发展和计算机技术的成熟，水资源优化调度技术及方法的相关研究更加丰富，包括线性规划方法[6]、动态规划方法[7]、多目标优化技术[8-11]、大系统分解协调技术[12]以及启发式智能算法[13-14]在内的一系列技术和方法得到广泛的应用与发展。随着多目标优化算法的发展，各种多目标遗传算法相继被提出。量子遗传算法(quantum genetic algorithm，QGA)是一种基于量子计算原理的概率优化的遗传算法[15-16]，是由Narayanan等[17]受量子计算思想启发，将量子多宇宙的概念引入遗传算法研究后提出，在遗传算法领域中发展迅速。多目标量子遗传算法(multi-objective quantum genetic algorithm，MOQGA)是在量子遗传计算原理和多目标进化算法的基础上提出的[18]，虽在一定程度上改善了多目标遗传算法缺点，但仍然存在局部收敛、Pareto前沿分布不均匀等问题。通过对量子旋转门的改善、加入量子交叉、加入量子灾变操作以及外部档案集维护策略等方式是实现MOQGA改进的一种新思路。

本研究以受水区需水满足度最大、系统总抽水量最小为优化目标，构建南水北调东线工程江苏段水资源优化调度模型，采用改进的MOQGA算法求解，运用组合赋权方法对非劣解集进行多属性决策，提出南水北调东线工程江苏段水资源优化调度方案。

1 研究区概况及系统概化

南水北调东线工程江苏段地处淮河及沂沭泗流域的下游，涉及扬州、淮安、盐城、宿迁、连云港和徐州6市，输水干线长达404 km。该工程是在已有的江水北调工程基础上逐步扩大调水规模并向北沿伸，新建宝应站、淮安四站等11座泵站，改扩建泗阳站、刘山站等3座泵站，加固改造江都三站、四站等4座泵站，形成了运河线、运西线双线输水格局。根据南水北调东线工程江苏段主要组成以及骨干河渠间的连接关系进行系统概化，将受水区划分为了18个计算分区，其中安徽与山东两省分别作为1个计算分区，江苏省内的计算分区在江淮区间、洪泽湖区间、洪骆区间、骆马湖区间、骆微区间和南四湖区间的划分基础上细分为16个计算分区，见图1。

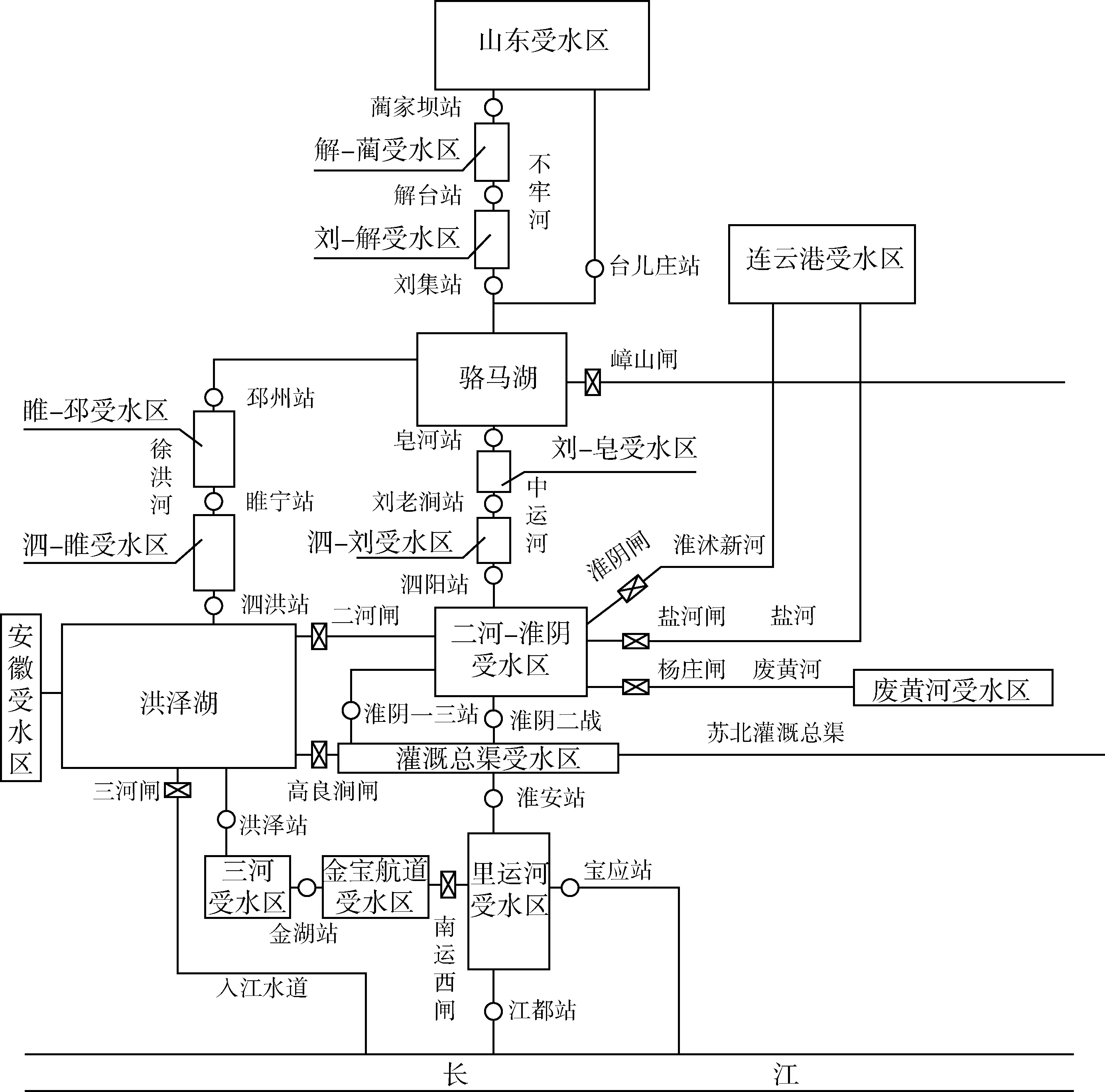
图1 南水北调东线工程江苏段系统概化

2 南水北调东线工程江苏段水资源优化调度模型

2.1 目标函数

南水北调东线工程江苏段作为国家公益性的跨流域调水工程，系统缺水情况应作为衡量优化效果的一个重要指标；其次，工程必须考虑运营成本，泵站抽水量的多少将直接决定工程的运行成本，因而也应作为一个优化目标。本研究综合考虑受水区需水满足度最大和系统总抽水量最小两个目标，确立优化调度模型的目标函数，计算公式为

(1)

(2)

式中：t为时段序号，t=1,2,…,T，本研究中T=12；i为分区编号，i=1,2,…,N，本研究中N=16；j为泵站编号，j=1,2,…,M，本研究中M=16；QX(i,t)为t时段i分区的需水量，亿m3；QG(i,t)为t时段i分区的实际供水量，亿m3；QS(j,t)为t时段j泵站的抽水量，亿m3。

2.2 约束条件

a. 湖泊水量平衡约束。湖泊通过图2的“湖-河网”水量交换子系统方式运行，并满足水量平衡方程：

S(i,t+1)=S(i,t)+Q(i,t)+PI(i,t)+

FI(i+1,t)-PO(i,t)-W(i,t)-FO(i,t)

(3)

式中：S(i,t)为t时段i湖泊的蓄水量，亿m3；i为湖泊编号(1—洪泽湖、2—骆马湖、3—下级湖)；Q(i,t)为t时段i湖泊的入湖径流量，亿m3；W(i,t)为t时段i湖泊供水量，亿m3；PI(i,t)为t时段i湖泊的抽河网北调入湖量，亿m3；PO(i,t)为t时段i湖泊的抽湖北调水量，亿m3；FI(i,t)为t时段河网泄入i湖泊的水量，亿m3；FO(i,t)为i湖泊t时段下泄入河网的水量，亿m3。

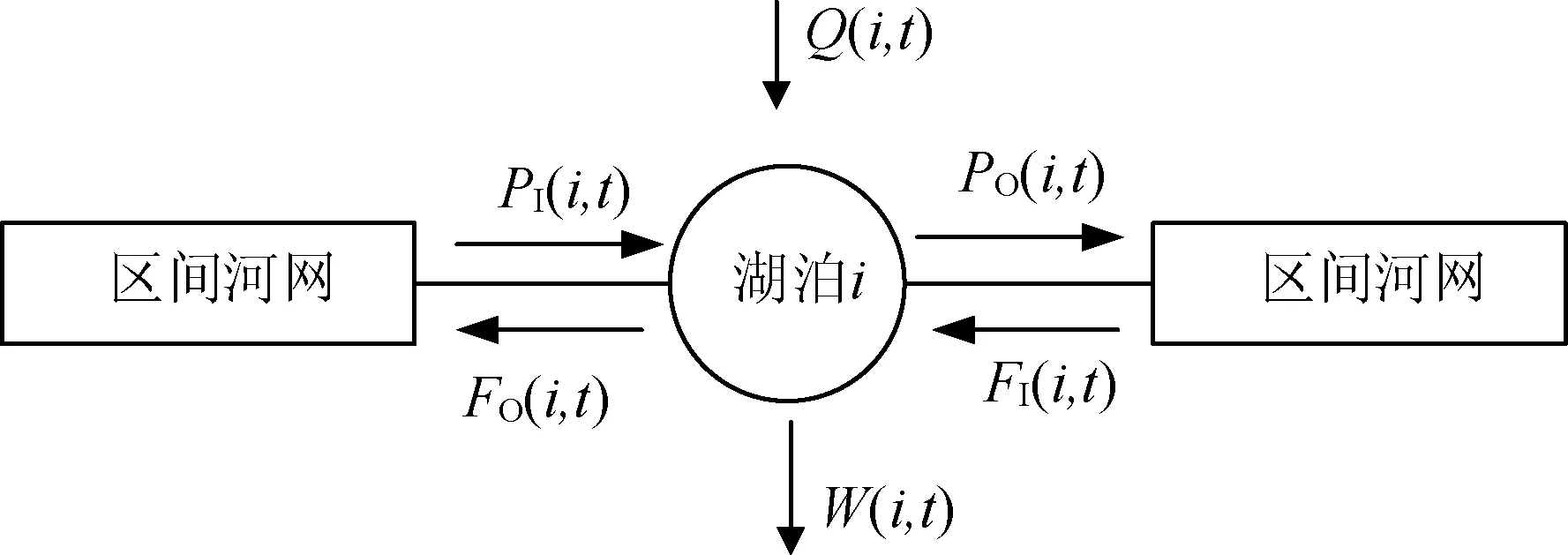
图2 “湖-河网”水量交换子系统

b. 湖泊调蓄能力约束。

Smin(i,t)≤S(i,t)≤Smax(i,t)

(4)

式中，Smin(i,t)和Smax(i,t)分别为i湖泊t时段的最小蓄水能力(死库容)和最大蓄水能力(蓄满库容)，亿m3。

c. 泵站工作能力约束。

PI(i,t)≤PImax(i,t)

(5)

PO(i,t)≤POmax(i,t)

(6)

式中，PImax(i,t)、POmax(i,t)分别为相应泵站的最大抽水能力，亿m3。

d. 控制闸站最大过流能力约束。

FO(i,t)≤FOmax(i,t)

(7)

FI(i,t)≤FImax(i,t)

(8)

式中，FImax(i,t)、FOmax(i,t)分别为相应控制闸站的最大过流能力，亿m3。

e. 北调控制水位约束。一般情况下，当湖泊水位低于控制水位时，停止抽湖泊既有蓄水北调，具体见表1。

表1 调蓄湖泊北调控制水位 m

f. 非负约束。即所有的流量都要大于0。

3 基于改进的MOQGA的模型求解

传统的MOQGA存在易陷入局部最优解、全局寻优效率低、Pareto前沿分布不均匀的问题。本研究对MOQGA作了如下改进：①通过对量子旋转门的改进，加入量子交叉、量子灾变操作等方式对传统的QGA进行改进；②基于Sigma选取策略，选择全局向导维护外部档案集。

3.1 算法设计

3.1.1 改进的QGA

QGA将量子力学中的量子比特[19]、量子态叠加等概念运用于遗传算法中，通过将量子旋转门作用于染色体基因的更新调整，完成进化操作。在传统QGA中，用量子比特来表示染色体，用量子比特的概率幅表示染色体的编码，种群更新和染色体的交叉是最关键的进化方式，一般采用量子门完成更新操作，公式为

(9)

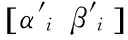
本研究通过采用自适应性旋转角度、修正概率幅值两方面对传统量子旋转门进行改进。同时，采用全干扰交叉操作增加种群的多样性，防止未成熟收敛，并使用群体灾变策略避免算法陷入局部寻优[4]。自适应性旋转角度Δθ′的表达式为

Δθ′=θmin+K(θmax-θmin)

(10)

其中

式中：θmin为Δθ′的固定值的最小值，取0.001π；θmax为Δθ′的固定值的最大值，取0.05π；K为调整系数；fmax和fx分别为搜索到的最优个体适应度和当前个体的适应度值；N1为当前迭代次数；N2为最大迭代次数。

(11)

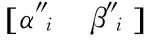
3.1.2 基于Sigma选取策略选择全局向导维护外部档案集

在单目标粒子群优化算法中，全局最优粒子的选取可以通过比较适应度函数进行优劣比较，而在多目标优化问题中，迭代求解得到的Pareto非劣解集无法通过一个标准的方法来判断优劣，使得全局向导的选取变得复杂。基于Sigma选取策略来选择全局向导是目前常用的方法[20]。

以双目标问题为例，f1和f2分别代表两个目标，f2=αf1(α>0)表示在二维空间中斜率为α的直线公式，则在该直线上的点均被赋予同一个Sigma值σ，公式为

(12)

首先将Sigma值σ赋给外部档案Np里的每一个成员，种群Na里的每一个粒子均被赋予一个Sigma值σi，通过计算所有σ与σi的欧氏距离，选取Sigma值最为接近粒子i的档案成员便作为该粒子的向导，公式为

(13)

式中，σl为外部档案Np里的每一个粒子的Sigma值。

3.2 改进的MOQGA算法流程

综上所述，改进的MOQGA的基本步骤如下：

步骤1：设置初始种群规模g，量子位数目m，全局迭代次数Nmax,gen，旋转角度算子[δmin,δmax]，外部归档集规模NEA。

步骤2：基于量子二链编码方案生成初始解种群，初始全局迭代次数Ngen=1，外部归档集赋空集。

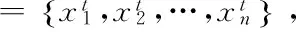
步骤4：进行解空间的转换，计算个体的各个目标函数值，并对种群个体实施非支配排序，基于Sigma选取策略选择全局向导维护非劣解外部档案集。

步骤5：根据量子旋转角的调整策略计算旋转角Δθ，并对量子旋转门操作后的概率幅进行修正，实现Na(t)更新。

步骤6：进行量子交叉操作，判断是否需要进行量子灾变，如果满足，则进行量子灾变操作；如果不满足，则进行步骤7。

步骤7：检查是否满足算法终止条件，若满足终止条件，停止迭代并输出结果，否则转到步骤3。

3.3 算法测试

为了验证算法的可行性与优越性，采用ZDT测试函数(ZDT1、ZDT2、ZDT3以及ZDT6)[21]对改进的MOQGA进行测试，并与传统的MOQGA求解结果进行对比。两种算法的参数设置为：粒子群种群规模为50，迭代次数为1000，外部档案Np为50，量子位数目M为20，交叉概率Pc为0.95，变异概率Pm均为0.05。图3是基于两种算法的ZDT测试函数的Pareto曲线。由图3可见，对于ZDT测试函数，改进的MOQGA的非劣解集均能够收敛到最优前沿，所得到的解优于传统MOQGA算法。

4 结果及分析

4.1 模型求解结果

对南水北调东线工程江苏段历史长系列径流资料进行分析，确定平水年、枯水年、特枯水年3个典型水文年，以水文年为计算周期，以月为计算时段，以洪泽湖、骆马湖以及下级湖入湖径流量资料为输入，各调蓄湖泊的起调水位为近年来对应时段多年平均水位，对南水北调东线工程江苏段进行优化调度研究。

采用改进的MOQGA求解多目标调度模型，迭代10 000次后得到的Pareto前沿，在平水年、枯水年、特枯水年3种来水条件下受水区需水满足度(目标1)的目标值范围分别为[81.10%，97.27%]、[70.67%，97.24%]、[29.64%，84.19%]，抽水量(目标2)的目标值范围为[59.74亿m3，132.68亿m3]、[95.72亿m3，282.29亿m3]、[160.29亿m3，543.89亿m3]，见图4。选取系统总抽水量、需水满足度、弃水量、抽江水量、汛末总蓄水量5个指标，采用组合赋权的多属性决策方法[22]，进行方案优选，得到不同典型年来水条件下的最优调度决策方案，各方案下主要抽水线路年调水量以及受水区全年实际供水情况详见表2～4。优化调度之后，平水年来水条件下系统总缺水量为3.44亿m3，总抽水量为132.68亿m3，其中抽江水量为0，总弃水量为49.83亿m3；枯水年来水条件下系统总缺水量为4.78亿m3，总抽水量为268.57亿m3，其中抽江水量为43.80亿m3，总弃水量为12.94亿m3；特枯水年来水条件下系统总缺水量为30.45亿m3，总抽水量为525.43亿m3，其中抽江水量为140.27亿m3，总弃水量为0。

(a) ZDT1

(b) ZDT2

(c) ZDT3

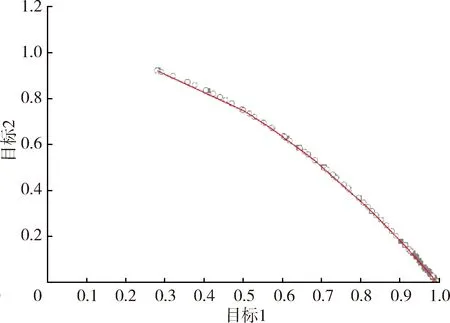
(d) ZDT6

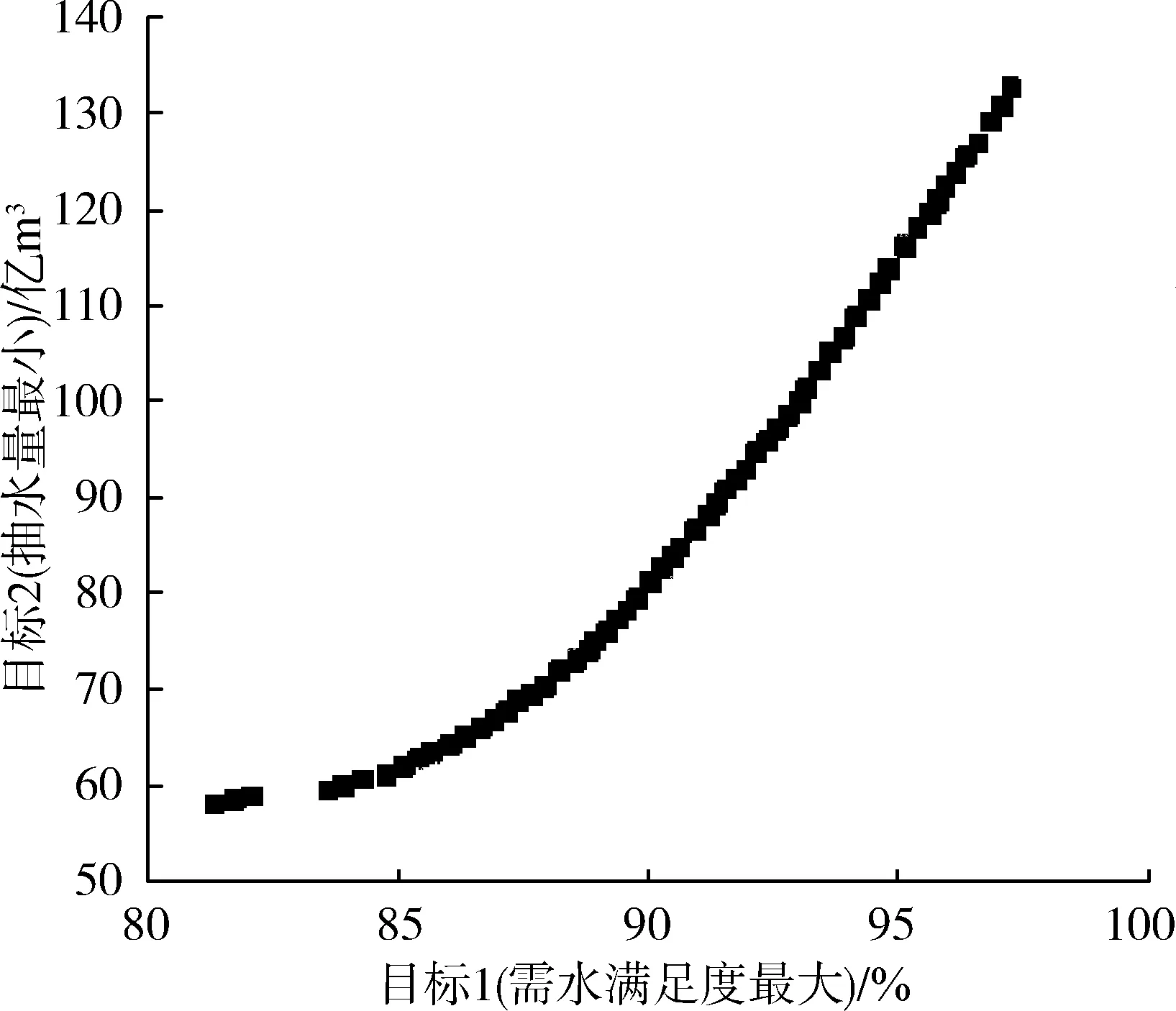
(a) 平水年

(b) 枯水年

(c) 特枯水年

表2 3种典型年下湖泊年调水量 亿m3

表3 3种典型年下湖间两线路年调水量 亿m3

表4 3种典型年下各受水区全年实际供水量 亿m3

4.2 与常规调度对比

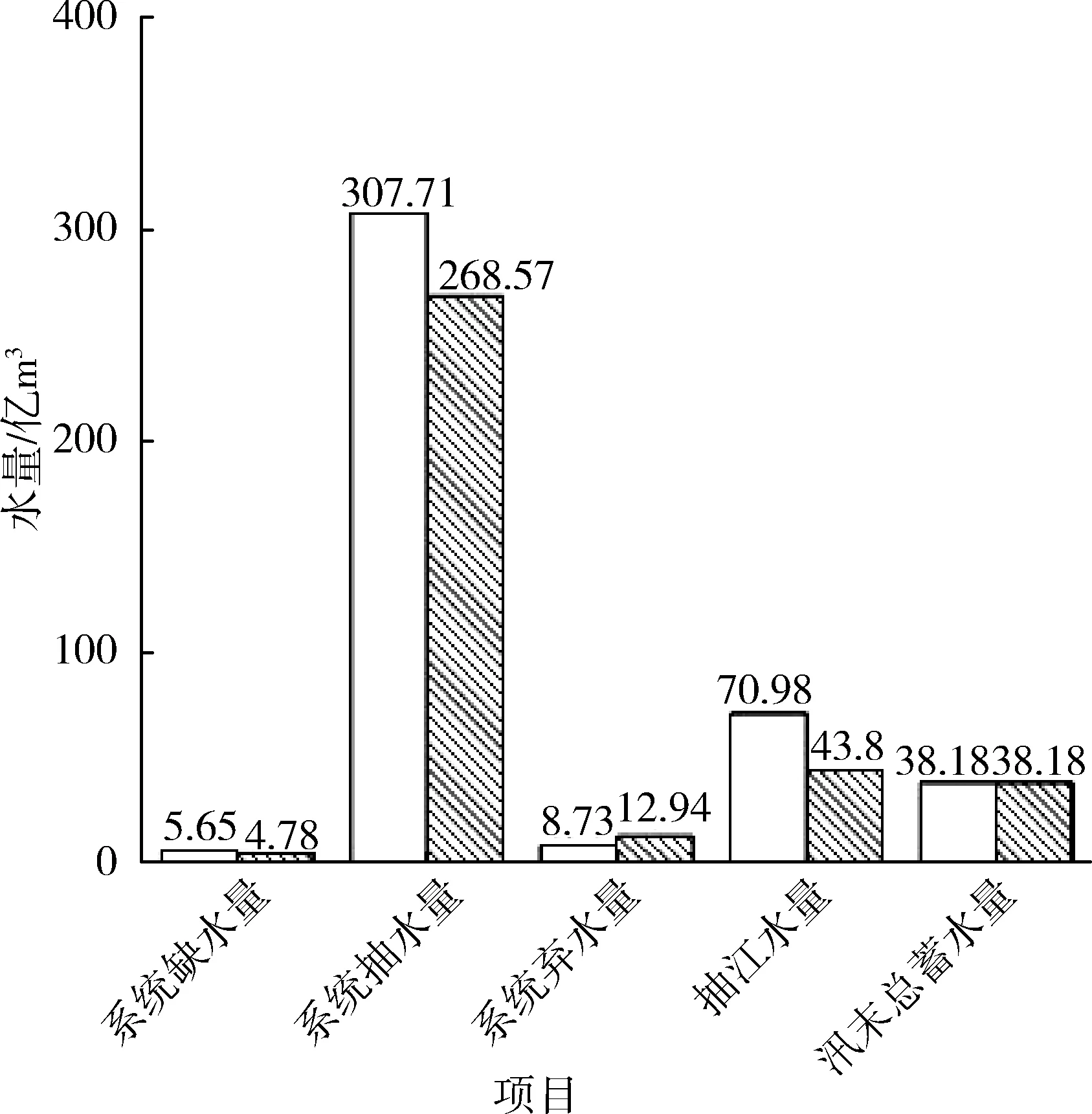
依据工程现行调度方案，模拟3种典型年来水条件下南水北调东线工程江苏段调度过程，从系统总抽水量、受水区缺水量、弃水量、抽江水量、汛末总蓄水量5方面对优化调度和常规调度结果进行对比分析，结果见图5。相对于常规调度，优化调度的受水区总缺水量在平水年来水条件下减少了0.89亿m3，在枯水年来水条件下减少了0.87亿m3，在特枯水年来水条件下减少了0.08亿m3，说明面对不同来水条件，优化调度模型均能通过合理调度减少受水区缺水状况，提高各用水户的需水满足度；平水年、枯水年、特枯水年3种典型年下系统总抽水量分别减少21.04亿m3、39.14亿m3和50.76亿m3，抽江水量分别减少了13.97亿m3、27.18亿m3和30.62亿m3，表明优化调度方式在充分利用淮河流域及沂沭泗流域的天然来水基础上，有效发挥湖泊的调蓄能力，使水资源得到合理分配。

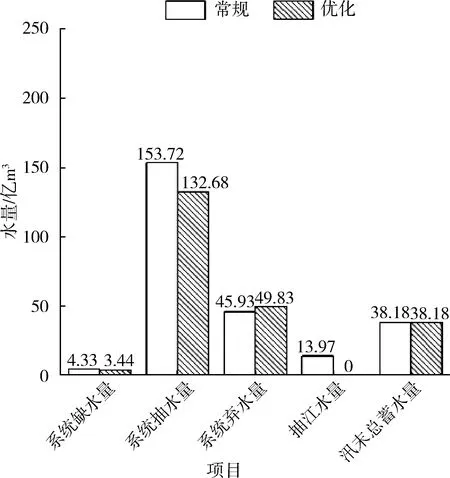
(a) 平水年

(b) 枯水年

(c) 特枯水年

5 结 论

针对南水北调东线工程江苏段水资源调度问题，以受水区需水满足度最大、系统总抽水量最小为优化目标，构建了南水北调东线工程江苏段水资源优化调度模型，采用改进的MOQGA算法求解，运用组合赋权方法对非劣解集进行多属性决策，提出南水北调东线工程江苏段水资源优化调度方案。优化调度方案能够充分利用湖泊的调蓄能力，提高各用水户的需水满足度，降低抽水成本。相对于常规调度，在平水年、枯水年和特枯水年3种典型年来水条件下，优化调度的受水区总缺水量分别减少了0.89亿m3、0.87亿m3和0.08亿m3；系统总抽水量分别减少21.04亿m3、39.14亿m3和50.76亿m3；抽江水量分别减少了13.97亿m3、27.18亿m3和30.62亿m3，具有显著效益。

[1]于凤存，方国华，王文杰，等.基于多目标遗传算法的南水北调东线工程湖泊群优化调度研究[J].灌溉排水学报，2016，35(3):78-85.(YU Fengcun，FANG Guohua，WANG Wenjie，et al.Optimized dispatching of the lake group system along the South-to-North Water Diversion Route based on the multi-objective genetic algorithm [J].Journal of Irrigation & Drainage，2016，35(3):78-85.(in Chinese))

[2]侍翰生，程吉林，方红远，等.南水北调东线工程江苏段水资源优化配置[J].农业工程学报，2012，28(22):76-81.(SHI Hansheng，CHENG Jilin，FANG Hongyuan，et al.Optimal allocation of water resources for Jiangsu section of South-to-North Water Transfer East Line Project[J].Transactions of the Chinese Society of Agricultural Engineering，2012，28(22):76-81.(in Chinese))

[3]王文杰，吴学文，方国华，等.南水北调东线工程江苏段水量优化调度研究[J].南水北调与水利科技，2015，13(3):422-426.(WANG Wenjie，WU Xuewen，FANG Guohua，et al.Optimal water operation in Jiangsu section of the South-to-North Water Diversion Project [J].South-to-North Water Transfers and Water Science & Technology，2015，13(3):422-426.(in Chinese))

[4]王攀，方国华，郭玉雪，等.水资源优化调度的改进量子遗传算法研究[J].三峡大学学报(自然科学版)，2016，38(5):7-13.(WANG Pan，FANG Guohua，GUO Yuxue，et al.Research on water resources optimal cheduling based on improved quantum genetic algorithm [J].Journal of China Three Gorges University(Natural Sciences)，2016，38(5):7-13.(in Chinese))

[5]闻昕，王志，方国华，等.基于改进多目标粒子群算法的南水北调东线江苏段工程联合优化调度研究[J].水资源与水工程学报，2017，28(3):110-116.(WEN Xin，WANG Zhi，FANG Guohua，et al.Study on optimal operation of Jiangsu section of estern route of South-to-North Water Diversion Project based on improved multi-objective particle swarm optimization algorithm [J].Journal of Water Resources & Water Engineering，2017，28(3):110-116.(in Chinese))

[6]都金康，李罕,王腊春,等.防洪水库(群)洪水优化调度的线性规划方法[J].南京大学学报(自然科学)，1995(2):301-309.(DU Jinkang，LI Han，WANG Lachun，et al.A linear programming for optimal operation of multireservoir flood control system[J].Journal of Naijing University (Natural Science)，1995 (2):301-309.(in Chinese))

[7]王丽萍，孙平，蒋志强，等.并行多维动态规划算法在梯级水库优化调度中的应用[J].水电能源科学，2015，33(4):1327-1335.(WANG Liping，SUN Ping，JIANG Zhiqiang，et al.Application of parallel multi-dimensional dynamic programming algorithm in cascaded reservoirs optimal operation [J].Water Resources and Power，2015，33(4):1327-1335.(in Chinese))

[8]TSAI W P，CHANG F J，CHANG L C，et al.AI techniques for optimizing multi-objective reservoir operation upon human and riverine ecosystem demands [J].Journal of Hydrology，2015，530:634-644.

[9]CHEONG T S，KO I，LABADIE J W.Development of multi-objective reservoir operation rules for integrated water resources management [J].Journal of Hydroinformatics，2010，12(2):185.

[10]王磊之,胡庆芳,戴晶晶,等.面向金泽水库取水安全的太浦河多目标联合调度研究[J].水资源保护，2017,33(5):61-68.(WANG Leizhi,HU Qingfang,DAI Jingjing,et al.Research on multi-objective joint operation of Taipu River oriented to water supply safety of Jinze Reservior [J].Water Resources Protection，2017,33(5):61-68.(in Chinese))

[11]张凯,沈洁.基于萤火虫算法和熵权法的水资源优化配置[J].水资源保护，2016,32(3):50-53.(ZHANG Kai,SHEN Jie.Optimal allocation of water resources based on firefly algorithm and entropy method [J].Water Resources Protection，2016,32(3):50-53.(in Chinese))

[12]李桂香，王挺，温进化.水资源优化配置的大系统分解协调模型研究[J].电脑知识与技术，2010(26):7346-7349.(LI Guixiang，WANG Ting，WEN Jinhua.The study on decomposition and coordination model of large-scale system in optimal allocation of water resources [J].Computer Knowledge & Technology，2010(26):7346-7349.(in Chinese))

[13]王凌.智能优化算法及其应用[M].北京：清华大学出版社，2001.

[14]闻昕，丁紫玉，方国华,等.气候变化下新安江-富春江水电站径流响应模拟及适应性调度研究[J].水资源保护，2017，33(4):10-19.(WEN Xin,DING Ziyu,FANG Guohua,et al.Study on runoff response simulation and adaptive scheduling of Xinanjiang-Fuchunjiang hydropower station under climate change [J].Water Resources Protection，2017，33(4):10-19.(in Chinese))

[15]DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multiobjective genetic algorithm:NSGA-II [J].IEEE Transactions on Evolutionary Computation，2002，6(2):182-197.

[16]LEE J C，LIN W M，LIAO G C，et al.Quantum genetic algorithm for dynamic economic dispatch with valve-point effects and including wind power system[J].International Journal of Electrical Power & Energy Systems，2011，33(2):189-197.

[17]NARAYANAN A，MOORE M.Quantum inspired genetic algorithm[C]// Proceedings of the IEEE International Conference on Evolutionary Computation.Piscataway:IEEE Press，1996:61-66.

[18]车海军，王亮亮，顾佳琪，等.基于自适应网格多目标量子遗传算法的轧制规程优化[J].塑性工程学报，2016，23(6):79-86.(CHE Haijun，WANG Liangliang，GU Jiaqi，et al.Rolling schedule optimization based on adaptive grid multi-objective quantum genetic algorithm [J].Journal of Plasticity Engineering，2016，23(6):79-86.(in Chinese))

[19]张葛祥，金炜东.量子遗传算法的改进及其应用[J].西南交通大学学报，2003，38(6):717-722.(ZHANG Gexiang，JIN Weidong.Improvement of quantum genetic algorithm and its application [J].Journal of Southwest Jiaotong University，2003，38(6):717-722.(in Chinese))

[20]MOSTAGHIM S，TEICH J.Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO)[M].Piscataway:IEEE Press,2003.

[21]ZITZLER E，DEB K，THIELE L.Comparison of multiobjective evolutionary algorithms:empirical results[J].Evolutionary Computation，2000，8(2)，173-195.

[22]孙才志，吴永杰，刘文新.基于熵权TOPSIS法的大连市水贫困评价及障碍因子分析[J].水资源保护，2017，33(4):1-8.(SUN Caizhi,WU Yongjie,LIU Wenxin.Application of TOPSIS method based on entropy weight to water poverty evaluation and obstacle indicator diagnoses for Dalian City[J].Water Resources Protection，2017，33(4):1-8.(in Chinese))