黄河流域Budyko方程参数n演变规律及其归因研究

王卫光，陆文君，邢万秋，李进兴，李长妮

(1. 河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2. 河海大学水文水资源学院，江苏 南京 210098；3. 河海大学地球科学与工程学院，江苏 南京 211100)

气候变化和人类活动对水文循环产生的影响一直是水文学家关注的焦点[1-2]。蒸散发作为陆面水循环中最重要的水文过程之一，迄今仍然是研究中的薄弱点[3]。关于蒸散发研究的基础理论较多，其中Budyko框架理论由于原理简单、物理机制明确，在基于气候-土壤-植被系统的气象学、水文学、生态水文学等研究中得到了广泛的应用[4]。自1948年以来，众多关于Budyko框架的经验公式被提出，其中含有参数的经验公式在区域上对 Budyko 曲线的拟合精度较高，运用较广。1979年，崔启武等[5]首次将反映流域下垫面特征的参数n引入到Budyko方程中。目前在国内大多数的研究中，参数n都被当作恒定值来处理[6-8]。但事实上，恒定不变的参数n并不能很好地模拟流域水文状况，因为不仅气候变化会影响参数n，人类对水资源的不断开发利用、城市经济的发展等都会改变n值，影响降雨产汇流过程，进而改变水资源的时空分布格局。因此，研究参数n随时间的演变规律及其驱动机制很有必要。

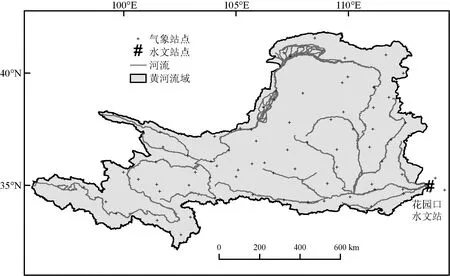
图1 研究区的气象站点和水文站点分布

黄河流域流经不同气候区，流域气候和地貌差异显著[9]，在气候变化和人类活动的共同影响下，参数n变异的情况更复杂，但关于此流域参数n的演变规律和归因分析却未见报道。因此，本文基于花园口控制站以上黄河流域内76个气象站1956—2000年的逐日气象观测资料，和花园口水文站1956—2000年的逐月径流深(图1)，运用移动窗口法将Budyko方程的输入变量进行平滑和滤波处理后推算参数n，并在总结文献研究[10-12]的基础上，筛选出7个代表气候变化的因子：降水量(P)、温度(T)、潜在蒸发量(E0)、逐年最大日降水量(Pmax)、降水季节性指标(SI)、降雨集中度(CI)、气候干旱指数(PDSI)和3个反映人类活动的因子：人口状况(Pop)、生产总值(GGDP)和有效灌溉面积(Airr)，运用多元逐步回归模型、敏感性系数法和贡献评估法，定量评价黄河流域参数n的变化对气候变化和人类活动的响应。

1 研究方法

1.1 Budyko方程

Budyko方程描述了实际蒸发依赖于潜在蒸发量(热能来源)和可利用水量(水量来源)的程度[13]，利用Budyko 框架可以有效评价气候、植被和水文循环之间的相互影响[14]。其中经量纲分析和数学推导并被广泛应用的傅抱璞公式[15]可较好地表达流域内的水热耦合状态。Yang等[16]以傅抱璞公式为基础，对Choudhury公式变换成另一种表达Budyko曲线的方程为

(1)

式中：E为流域实际蒸发量，mm。

本文采用式(1)结合流域水量平衡方程(E=P-R)来推算Budyko方程中的参数n。

1.2 参数n各影响因子及计算方法

1.2.1 参数n各影响因子

a. 潜在蒸发量(E0)。计算潜在蒸发的方法主要可分为综合法、温度法、辐射法和水面蒸发量法，其中Penman-Monteith(PM)法由于具有明确的物理机制而成为FAO唯一推荐的方法[17]。因此，本文选取综合考虑了多种气象要素并经Shuttleworth于1993年修正的Penman-Monteith(PM)公式来计算E0。

(2)

式中：Δ为饱和水汽压曲线斜率，kPa /℃；γ为干湿常数，kPa /℃；Rn为净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；λ为潜热，MJ/kg；U2为2 m高处的风速，m/s；es为平均饱和水汽压，kPa；RH为相对湿度，%。

b. 逐年最大日降水量(Pmax)。根据中国气象数据网上的气象数据统计出流域逐年最大日降水量(Pmax)。

c. 降水季节性指标(SI)。选用Walsh等[18]的公式来计算降水季节性指标：

(3)

式中：SIi是第i年的SI；Ri为第i年的降水量，mm；Xin代表第i年n月份的降水量，mm。

对公式(3)求得的逐年SI取多年平均值即可得到本文所需的降水季节性指标。

d. 降雨集中度(CI)。采用Martin-vide[19]于2004年提出的计算降雨集中度方法，此方法用于研究区域的降水极值情况更直观，且简单易行[20]。根据降雨集中度的定义，累积降水量百分比(Y)和累积降水天数百分比(X)呈负的指数分布，即符合洛伦兹曲线分布：

Y=aXexp(bX)

(4)

式中的a、b是可用最小二乘法率定得到的系数。则

(5)

e. 气候干旱指数(PDSI)。气候干旱指数采用帕尔默干旱指数(Palmer drought severity index，PDSI)代表。PDSI是一个常用的干旱指标，不仅考虑当时的水分条件，而且考虑前期水分状况、持续时间，是个定量描述旱情的较好的指标，在水文、 气象、农业等领域广泛应用。

f. 人口状况(Pop，万人)、生产总值(GGDP，亿元)和有效灌溉面积(Airr，103hm2)。数据整理时，首先根据统计局官网年报整理得黄河流域流经各省的人口状况Pop、生产总值GGDP和有效灌溉面积Airr。将这些数据分别除以各省的行政区域面积即得各省的Pop密度、GGDP密度和Airr密度，然后乘以黄河流域在各省份分布的面积，最后将所得结果相加就可以得到黄河流域的人口状况(Pop)、生产总值(GGDP)和有效灌溉面积(Airr)。

1.2.2 影响关系的研究方法

a. 流域气象要素空间插值。黄河流域的降水(P)、平均气温(T)、最高气温、最低气温、相对湿度、平均风速和日照时数采用气象站点相应的气象数据通过插值方法获得。具体计算方法如下：①将研究区划分成10 km×10 km大小的网格；②根据网格内气象站点的数据通过反距离权重法得到每个网格的各气象要素值；③对覆盖整个研究区的所有网格的各气象要素值分别求平均，即可得到该研究区的气象要素值。

b. 平滑与滤波处理。移动窗口法(moving window)是简单且有效的平滑随机变化方法，被广泛应用于处理非平稳序列数据。在本文中，考虑到Budyko水热耦合平衡方程适用于多年平均尺度(一般多于10年)，该尺度下的流域蓄水变化几乎为0，并且受自然气候变化的影响小，因此将移动窗口定为11年，以1961年代表1956—1966年段，以此类推，2000年代表1995年以后的时段，然后对Budyko水热耦合平衡方程中的变量及各影响因子进行滑动平均。

c. 多元逐步回归模型(MSR)。为确定各影响因子对Budyko水热耦合平衡方程中参数n变化的影响，选用MSR模型来建立代表气候变化(P、E0、T、Pmax、SI、CI、PDSI)和人类活动(Pop、GGDP、Airr)的各因子对参数n的响应关系。

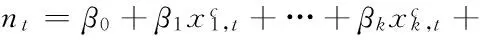
(6)

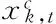
d. 敏感性系数法。为识别各因子对Budyko方程参数n变化的贡献，选用敏感性系数法来估算参数n的变化对各因子的敏感程度，计算公式为

(7)

式中：xi代表第i个自变量；S(xi)为参数n的变化对变量xi的敏感性系数；Δxi为第i个自变量的变化值；Δn为参数n的变化值。

e. 贡献评估法。数学上，对于函数y=f(x1,x2,…)，t时间序列的因变量y的变化可用微分方程表示：

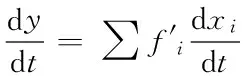
(8)

令

分别代表y和xi的长期序列的坡度值，式(8)可转换为

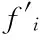
(9)

其中

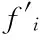
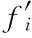
2 结果与分析

2.1 参数n的变化趋势

以P、R和E0的11年滑动平均值作为Budyko水热耦合平衡方程(式(1))的输入数据推算参数n。图2(a)为变化的参数n值序列与恒定n值(用实测P、R和E0的1956—2000年均值通过Budyko计算得到恒定n值)的比较。从图2(a)可以看出，从20世纪70年代初期到80年代中期滑动平均的参数n值在恒定n值上下波动，而20世纪70年代初期以前和80年代中期以后滑动平均的参数n值分别明显小于和大于恒定n值。滑动平均的参数n值在1961—2000年间呈现显著的上升趋势。

整个研究时段中变参数n的最大值为2.746，最小值为1.783，分别出现在1964年和1999年。将它们分别代入式(1)，计算得蒸发率(E/P)相对于干旱指数(E0/P)的分布(图2(b))。从图2(b)可以看出，在相同的干旱指数下，随着水热耦合状态改变(n的提升)，流域的蒸发率越大，即在降水量不变的条件下，黄河流域的n越大，蒸发越大，根据流域水量平衡方程(E=P-R)可知，径流越小，意味着整个流域越来越干旱。

(a) 恒定n值与滑动平均n值的比较

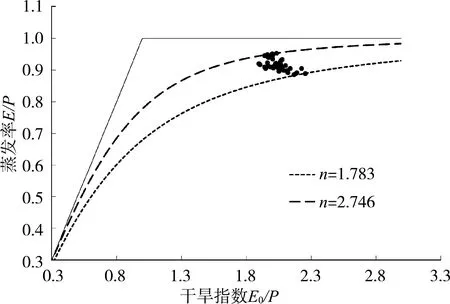
(b) 蒸发率(E/P)相对于干旱指数(E0/P)的分布

表1 黄河流域上反映气候变化和人类活动的10个因子的变化趋势及其显著性特征

注：“*”代表显著性通过0.05显著性检验。

此外，将滑动平均的参数n值与恒定n值分别代入到Budyko方程中计算的E与根据水量平衡(E=P-R)用实测P和R的滑动平均值计算的E进行比较，并选用纳西系数(NSEC)和平均相对误差(RE)来评价模型的模拟效果(图3)。由滑动平均的参数n计算的E与实测滑动平均值计算的E基本吻合，RE为0，NSEC达到1。而由恒定参数n计算的滑动平均窗口的E与实测滑动平均值计算的E有较大差距，RE为-0.031，NSEC为0.683。这说明恒定不变的Budyko水热耦合平衡方程参数n在模拟流域水文状况时效果较差，证实了研究变参数n的必要性。

2.2 参数n各影响因子的演变趋势

表1为黄河流域代表气候变化和人类活动特征的因子的变化趋势及其显著性检验。由表1可知，黄河流域1956—2000年的R、E0和PDSI呈现显著下降趋势，并且MK检验和T检验的结果一致。对于T，T检验结果显示其呈显著上升趋势，而MK检验结果并不显著。在其他代表气候变化的因子中，除了P呈非显著下降趋势外，Pmax、SI和CI均呈现非显著上升趋势。表明虽然黄河流域降水量在过去几十年有微弱的下降，但降水极值(Pmax、CI等)变化却愈发剧烈。

图4展示了各水文气象变量的时间序列以及11年滑动平均值。从图4可以看出，花园口水文站R从1985年开始持续下降，流域E0在1985年之后由下降趋势转为轻微的上升趋势，流域T则在1987年之后上升趋势更为明显，SI在1990年之后呈现明显的增加趋势,PDSI呈现持续下降的趋势，其他因子变化较为平缓。

图5为黄河流域反映人类活动特征的因子的变化趋势。结合表1可知流域Pop、GGDP和Airr均呈显著上升趋势(均通过MK检验和T检验)。流域Pop基本呈现线性增加趋势，GGDP在1985年之后迅速增加，而Airr则从20世纪80年代初增长变缓。

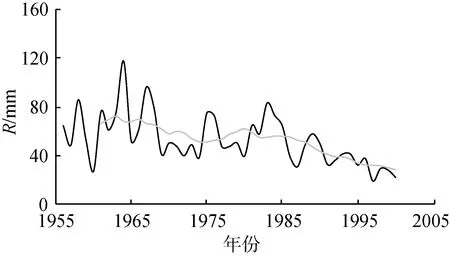
(a) 径流

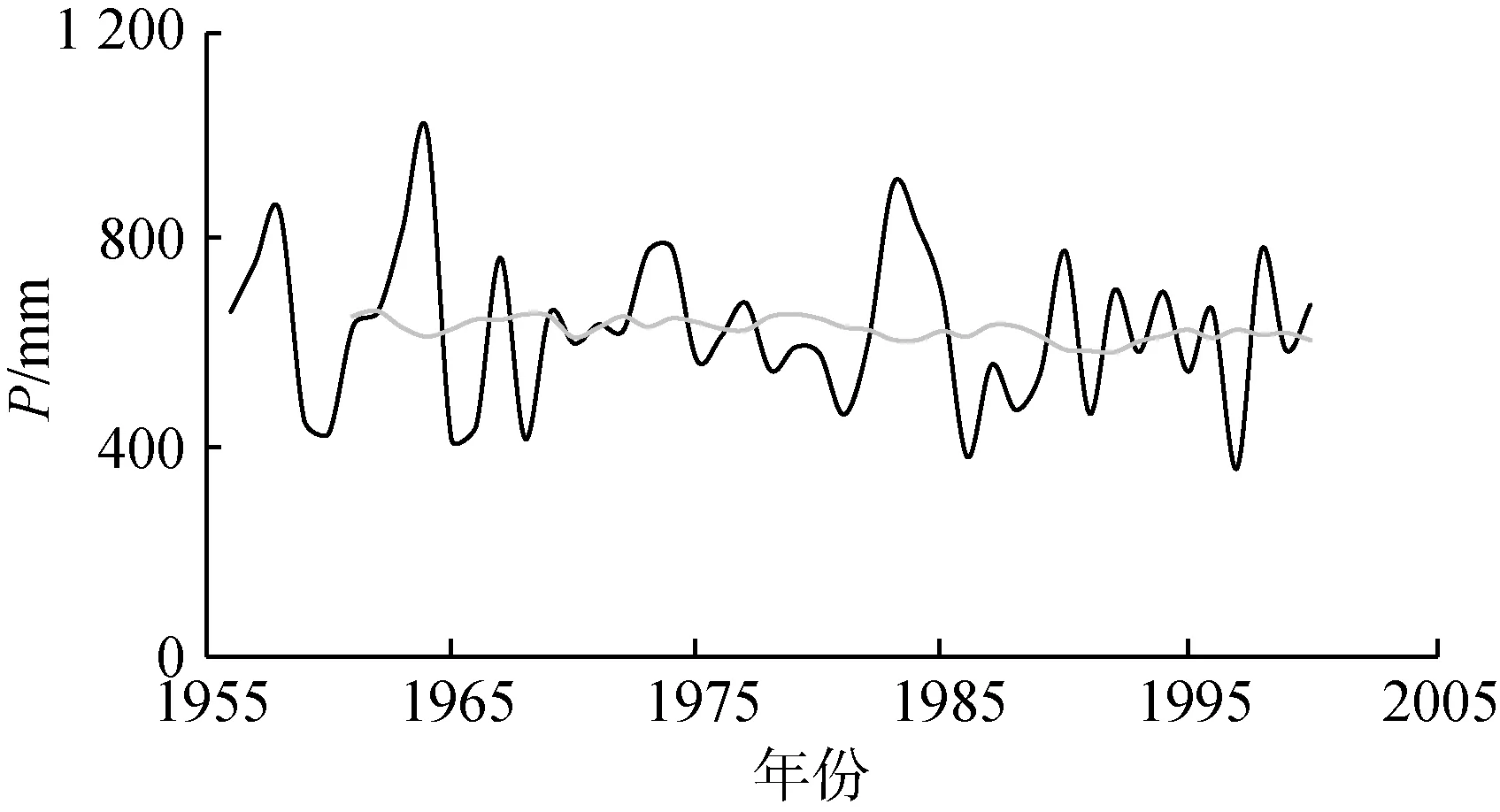
(b) 降水

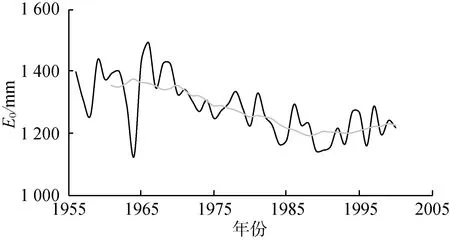
(c) 潜在蒸发

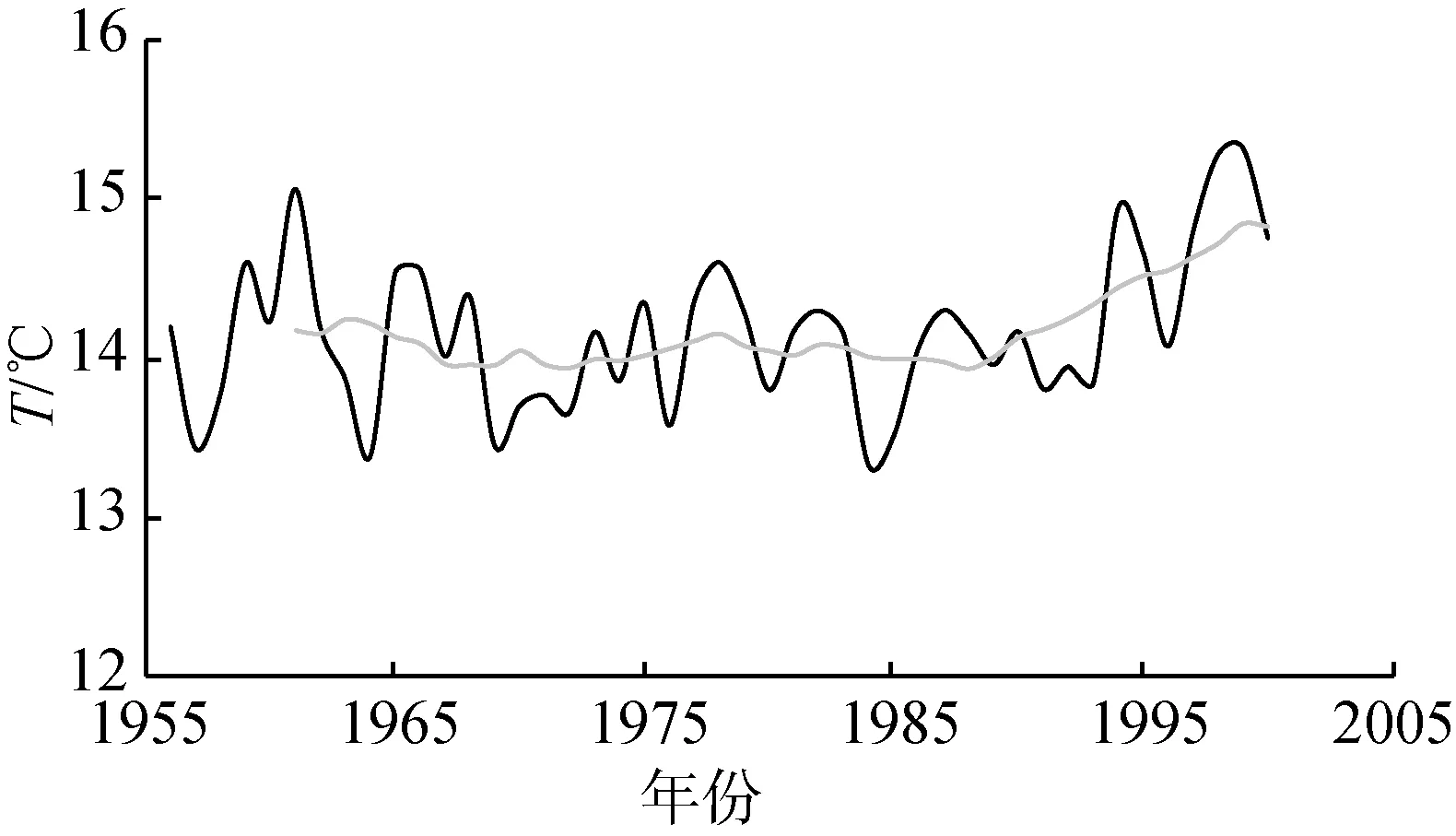
(d) 温度

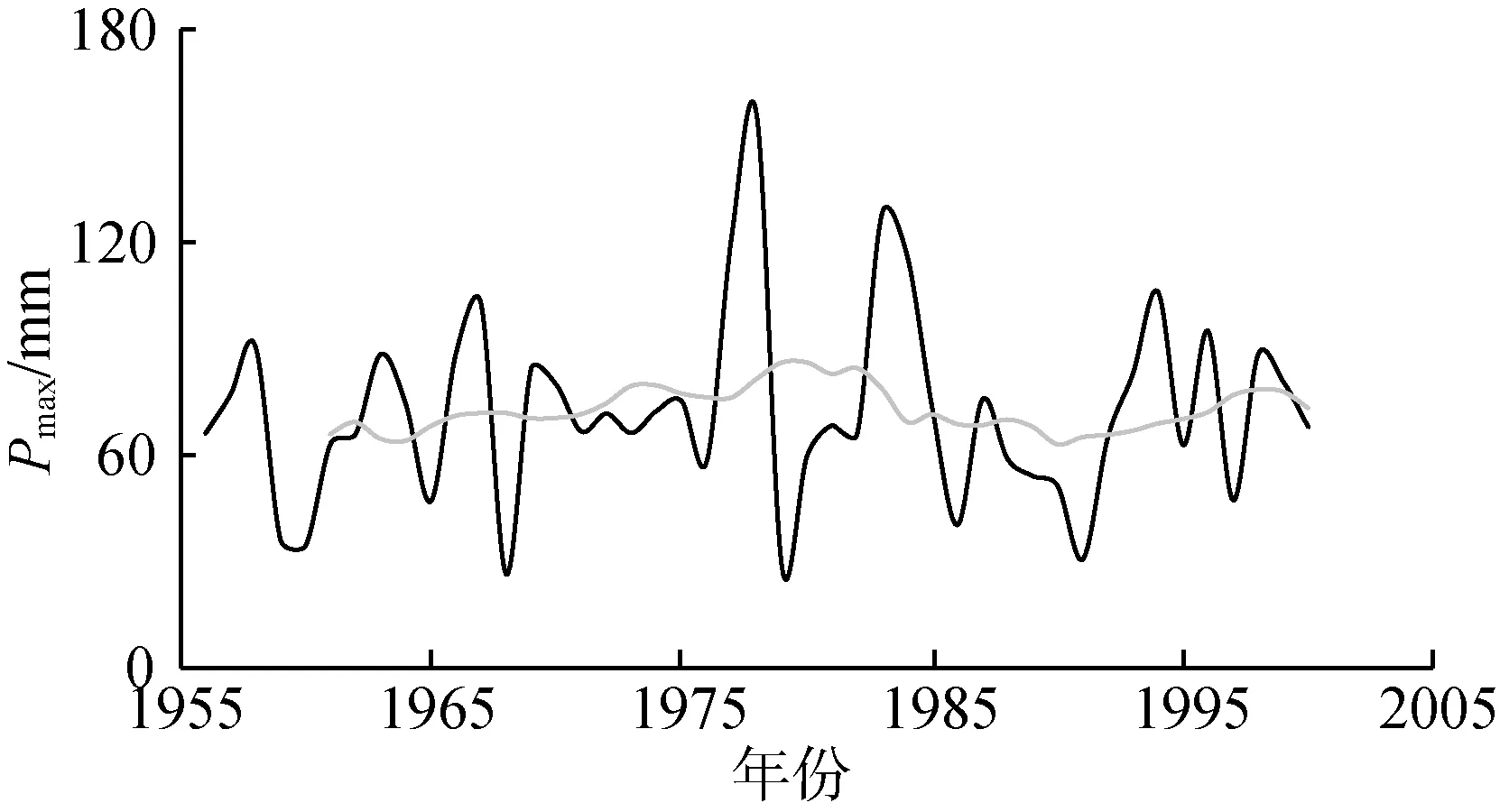
(e) 逐年最大日降水量

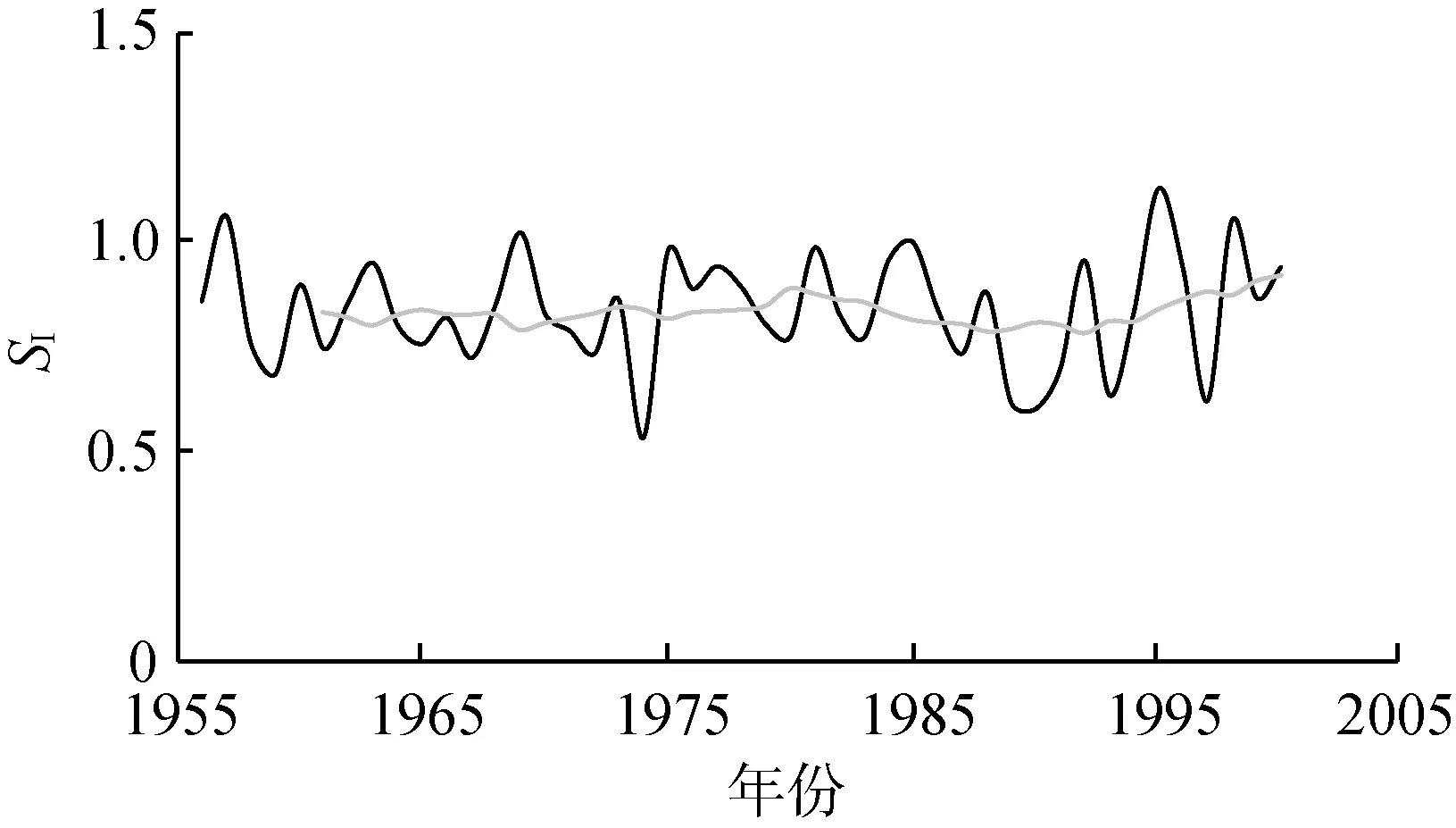
(f) 降水季节性指标

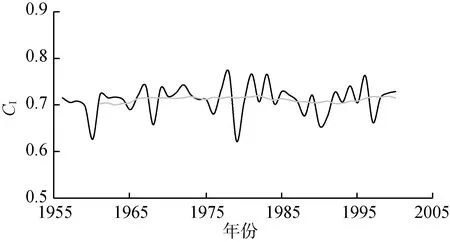
(g) 降雨集中度

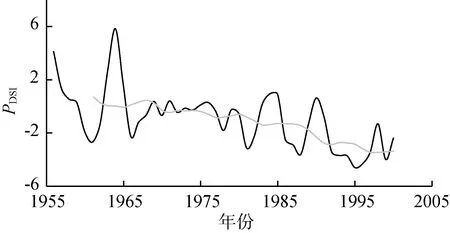
(h) 帕尔默干旱指数

(a) 人口

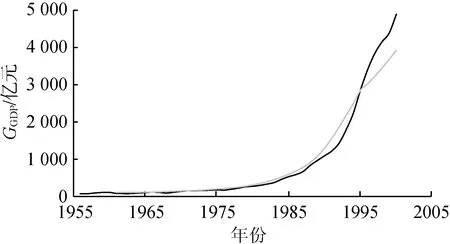
(b) 国民生产总值

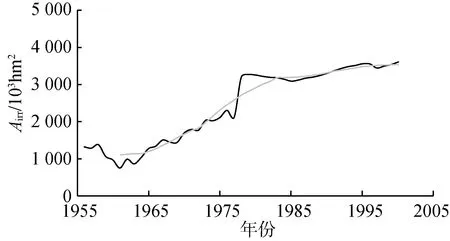
(c) 有效灌溉面积

2.3 参数n变化对各影响因素的响应关系

为进一步研究各变量对参数n变化的影响，运用MSR模型将代表气候变化的因子和人类活动的因子分别作为模型的自变量，参数n为因变量进行回归模拟。结果如下：

n=-1.886+0.00 416P+0.000 248Pop+
0.000 088 6GGDP-0.00 013Airr

(10)

由式(10)可知，与参数n变化最为相关的变量分别为P、Pop、GGDP和Airr。用实测P、Pop、GGDP和Airr代入公式(10)模拟的参数n和滑动参数n的结果见图6。从图6可以看出MSR模型对n值模拟效果较好，趋势线y=1.02x-0.06，R2为0.98，同时说明参数n确实受P、Pop、GGDP和Airr的影响较大。

图6 MSR模型模拟n值和滑动n值的比较

2.4 影响因子变化对参数n的影响评估

依据研究区MSR模型结果(式(10))进行敏感性系数和贡献率的计算，结果见表2。由表2可知，Budyko方程参数n的变化对P最为敏感，敏感性系数值达到1.169；而对Pop、GGDP和Airr的敏感性系数值分别为0.795、0.038和-0.152。表2同时列出了这4个因子对参数n变化的贡献率，Pop和GGDP对参数n的增加起到促进作用，并且Pop的贡献最大，贡献率为128.7%。P和Airr对参数n值的增加起到抑制作用，贡献率分别为-20.2%和-44.3%。总之，气候变化和人类活动对参数n值变化的贡献分别为-20.2%和120.2%，气候变化中P抑制了Budyko方程参数n值的增加，而人类活动的加剧促进了参数n的增加。

表2 P、Pop、GGDP、Airr对参数n变化的敏感性系数和贡献率

3 结 论

a. 黄河流域的Budyko方程参数n在1956—2000年间呈现增加的趋势，相应地，蒸散发也增加，从而出现了黄河流域的径流在1956—2000年间减小的现象。

b. 黄河流域Budyko方程参数n的变化与气候变化和人类活动均相关。P的变化对参数n的影响最大，对参数n的升高起到反作用。人类活动(Pop、GGDP和Airr)对参数n的变化也较为敏感，人类活动的加剧对参数n的增加起到促进作用。

c. 在黄河流域，人类活动对Budyko方程中参数n变化的贡献率比气候变化的贡献率更大，而在气候因子中，降水和潜在蒸发对参数n变化的贡献率最大。

[1]李洋洋，白洁芳，周维博，等.灞河流域气候因子对水沙变化的影响[J].水资源保护，2017，33(5):98-105.(LI Yangyang,BAI Jiefang,ZHOU Weibo,et al.Impact of climate factors on variations of water and sediment in Bahe River Basin [J].Water Resources Protection,2017,33(5):98-105.(in Chinese))

[2]郭巧玲，韩振英，丁斌，等.窟野河流域径流变化及其影响因素研究[J].水资源保护，2017，33(5):75-80.(GUO Qiaoling,HAN Zhenying,DING Bin,et al.Study of runoff variation characteristics and influence factors in Kuye River [J].Water Resources Protection,2017,33(5):75-80.(in Chinese))

[3]ZHANG Yongqiang,LIU Changming,TANG Yanhong,et al.Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau [J].Journal of Geophysical Research:Atmospheres,2007,112(D12):1103-1118.

[4]ZHANG Lu,POTTER N,HICKEL K,et al.Water balance modeling over variable time scales based on the Budyko framework-Model development and testing [J].Journal of Hydrology,2008,360(1/2/3/4):117-131.

[5]崔启武，孙延俊.论水热平衡联系方程[J].地理学报，1979，34(2):9-17.(CUI Qiwu,SUN Yanjun.On the correlative equation of the heat and water balance [J].Acta Geographica Sinica,1979,34(2):9-17.(in Chinese))

[6]栗铭，陈喜.基于Budyko假设的海河流域蒸散发量和径流量估算研究[J].中国农村水利水电，2014(6):107-111.(LI Ming,CHEN Xi.Research on the estimation of the evaporation and the runoff in the Haihe River Based on Budyko hypothesis [J].China Rural Water and Hydropower,2014(6):107-111.(in Chinese))

[7]郭生练，郭家力，侯雨坤，等.基于Budyko假设预测长江流域未来径流量变化[J].水科学进展，2015，26(2):151-160.(GUO Shenglian,GUO Jiali,HOU Yukun,et al.Prediction of future runoff change based on Budyko hypothesis in Yangtze River basin [J].Advances in Water Science,2015,26(2):151-160.(in Chinese))

[8]许珊珊，金亦，刘金涛，等.Budyko理论在水文气候分区中的应用研究[J].中国农村水利水电，2017(3):17-20.(XU Shanshan,JIN Yi,LIU Jintao,et al.The application of Budyko theory to hydro-climatic classification [J].China Rural Water and Hydropower,2017(3):17-20.(in Chinese))

[9]韩艳利，娄广艳，葛雷，等.黄河流域与水有关生态补偿框架的探讨[J].水资源保护，2016，32(6):142-150.(HAN Yanli,LOU Guangyan,GE Lei,et al.Discussion of water-related ecological compensation framework for Yellow River Basin [J].Water Resources Protection,2016,32(6):142-150.(in Chinese))

[10]YANG Dawen,SUN Fubao,LIU Zhiyu,et al.Analyzing spatial and temporal variability of annual water-energy balance in nonhumid regions of China using the Budyko hypothesis [J].Water Resources Research,2007,43(4):436-451.

[11]SHAO Quanxi,TRAYLEN A,ZHANG Lu.Nonparametric method for estimating the effects of climatic and catchment characteristics on mean annual evapotranspiration [J].Water Resources Research,2012,48(3):949-960.

[12]WILLIAMS C A,REICHSTEIN M,BUCHMANN N,et al.Climate and vegetation controls on the surface water balance:synthesis of evapotranspiration measured across a global network of flux towers [J].Water Resources Research,2012,48(6):327-40.

[13]BUDYKO M I.Climate and life [M].New York：Academic Press,1974.

[14]DONOHUE R J,RODERICK M L,MCVICAR T R.On the importance of including vegetation dynamics in Budyko's hydrological model [J].Hydrology and Earth System Sciences,2006,11(2):983-995.

[15]傅抱璞.论陆面蒸发的计算[J].大气科学,1981,5(1):23-31.(FU Baopu.Calculation on land surface evaporation [J].Scientia Atmospherica Sinica,1981,5(1):23-31.(in Chinese))

[16]YANG Hanbo,YANG Dawen,LEI Zhidong,et al.New analytical derivation of the mean annual water-energy balance equation [J].Water Resources Research,2008,44(3):893-897.

[17]ALLEN R G,PEREIRA L S,RAES D,et al.Crop evapotranspiration guidelines for computing crop water requirements [M].Rome:Fao Irrigation and Drainage Paper,1998:56.

[18]WALSH R P D,LAWLER D M.Rainfall seasonality:description,spatial patterns and change through time [J].Weather,1981,36(7):201-208.

[19]MARTIN-VIDE J.Spatial distribution of a daily precipitation concentration index in peninsular Spain [J].International Journal of Climatology,2004,2(8):2709-2729.

[20]邢万秋，王卫光，吴杨青，等.淮河流域降雨集中度的时空演变规律分析[J].水电能源科学，2011，29(5):1-5.(XING Wanqiu,WANG Weiguang,WU Yangqing,et al.Change properties of precipitation concentration in Huaihe River Basin [J].Water Resource and Power,2011,29(5):1-5.(in Chinese))