冗余驱动两轴电液角振动台控制方法研究
关广丰, 熊 伟, 王海涛
(大连海事大学 机械工程系,辽宁 大连 116026)
振动模拟实验通过在实验室中再现环境振动条件,检验结构或试件的可靠性[1-2]。地震模拟实验中,通过对缩尺模型的振动测试,分析建筑物的抗震性能。受模型尺寸效应及动力相似性条件限制,很难根据缩尺模型实验结果确定原结构的动力反应特性[3-4]。为满足大型复杂结构足尺模型振动实验的需求,研制大型振动台成为振动环境模拟的主要发展方向[5-6]。日本防灾科学技术研究所于2005年建成了世界上最大的三轴六自由度E-defense振动台,承载能力达1 200 t[7]。
大型振动台多采用冗余驱动结构,以增强系统抗倾覆力矩的能力,改善振动台的加速度均匀度及横向分量指标[8]。但冗余驱动结构增加了控制系统的复杂性,如果控制策略选取不当,将使系统中各激振器间出现较大的内力耦合,过多消耗能量,严重时可导致振动台无法运动[9]。
冗余驱动多轴电液振动台控制系统主要由加速度控制回路和内力协调控制回路组成。传统加速度控制回路中,利用合成矩阵将铰点空间内的单缸信号转换为工作空间内的自由度信号[10]。受零位线性化假设条件的限制,振动台在大角度运动时,信号转换之间将出现较大偏差。基于运动学分析的控制方法,有利于提高系统在大位移条件下的控制精度[11]。
对于冗余驱动机构的内力协调控制问题,文献[12-13]提出基于逆动力学模型进行冗余驱动系统的内力协调。文献[14]基于台阵系统的传递函数模型设计内力协调控制器。受模型精度影响,上述方法工程实现比较困难。文献[15]提出基于零位线性化方法求取冗余力变换矩阵,调节内环力控制器参数。由于冗余力变换矩阵为常值,与实际工况相比存在偏差[16]。
本文首先对冗余驱动振动台进行运动学分析,利用位姿正解及Jacobian矩阵实现铰点空间信号与工作空间信号的转换,设计加速度控制回路。然后基于振动台动力学方程,设计内力协调控制回路。最后通过实验检验控制器的效果。
1 冗余驱动电液振动台控制系统结构
本文以两轴电液角振动台为研究对象,设计控制系统。图1所示为初始状态下振动台结构示意图,表1给出了振动台主要技术参数。
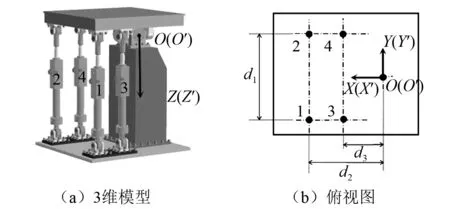
图1 冗余驱动角振动台结构示意图Fig.1 Redundantly driven angle shaking table structure

参数数值平台质量/kg300平台转动惯量/(kg·m2)[283561]油源压力/MPa10液压缸行程/m±0.075最大加速度/g±2d1/m0.8d2/m0.7d3/m0.4中位时液压缸上下铰点间的距离/m1.072大虎克铰中心到液压缸上铰点平面的垂直距离/m0.025
如图1所示,大虎克铰的中心为振动台的转动中心。振动台有rx(绕X轴)和ry(绕Y轴)两个转动自由度,由4个液压缸驱动,属于冗余驱动机构。振动台控制系统结构如图2所示。
控制系统主要由加速度控制回路①和内力协调控制回路②两部分组成。加速度控制回路由三状态控制器和运动学分析组成,使得振动台系统能够按照指令加速度运动。内力协调控制回路用于削弱系统中各缸间的内力耦合。图中Kact为单缸增益向量,用于微调各缸动态特性使其保持基本一致。下面详细叙述加速度回路及内力协调回路的原理及实现方式。
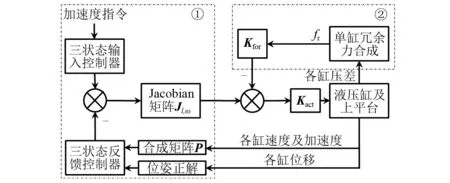
图2 冗余驱动电液振动台控制系统结构Fig.2 Control structure of the redundantlyactuated electro-hydraulic shaking table
2 加速度控制回路设计
基于并联机构学理论,对冗余振动台进行运动学分析,实现铰点空间信号与工作空间信号之间的变换。
位姿正解是由液压缸位移求取平台位姿的过程。如图1所示,分别建立静坐标系OXYZ和体坐标系O′X′Y′Z′,两个坐标系的原点均位于在大虎克铰的中心。静坐标系静止不动,体坐标系随上平台一起运动。初始状态时,两个坐标系重合。
定义R为体坐标系到静坐标系的3×3旋转变换矩阵;Ai(i=1,…,4)为4个液压缸上铰点在坐标系O′X′Y′Z′中的坐标,Bi为4个液压缸下铰点在坐标系OXYZ中的坐标;Li为液压缸长度向量。由空间向量关系可得
Li=RAi-Bi
(1)
式(1)可整理为
(2)
式中:li为第i号液压缸的长度;q为平台位姿。采用Newton-Raphson方法迭代求解式(2)所示的非线性方程组[17]
(3)
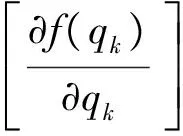
(4)
式中:Ln为液压缸单位方向向量组成的矩阵。
对于冗余驱动振动台,Jl,ω非方阵,其广义逆不唯一,导致利用式(4)及其导数求得的上平台速度及加速度的解不唯一。
电液振动台大多工作在中位附近,Jacobian矩阵在运动过程中变化较小,其导数可近似为零[19]。进一步综合考虑传感器及信号调理电路的信噪比、算法的执行周期等因素,实际控制系统中多采用自由度合成矩阵将单缸速度/加速度转换为平台的角速度/角加速度[20]。由图1,可得自由度合成矩阵P为
(5)
除上述分析的位姿运动学正解及Jacobian矩阵外,图2所示加速度控制回路中的三状态控制器,是电液振动台经典控制策略,主要用于实现振动台各自由度加速度指令的再现,相应控制器设计理论及实现方式可参考文献[7],此处不再赘述。
3 内力协调控制回路设计
基于并联机构学理论,采用牛顿欧拉法可得冗余驱动多轴振动台动力学方程为
(6)
式中:fa为铰点空间液压缸驱动力向量;fq为工作空间驱动力向量。
由冗余驱动系统分析可知,fa由两部分组成
fa=fy+fr
(7)
式中:fy为驱动平台产生刚体位移的力;fr为冗余力,使平台产生变形位移。
将式(7)代入式(6)中,有
(8)
式中:fy和fr可分别看作非齐次线性方程组的特解和通解。由于通解fr对外不做功,所以有
(9)
式(9)为齐次线性方程组,结合实际振动台系统,可取fr为
(10)
式中:上标“+”为矩阵的Moore-Penrose伪逆。式(10)用于在线计算各缸冗余力。取内力协调回路的控制器为比例控制器,协调系统内力,如图2所示。图中的Kfor即为比例控制单缸增益调节向量,用于保证内力协调回路的稳定性。
4 实验研究
实验系统如图3所示。冗余驱动电液振动台控制系统基于Matlab/XPC控制模式架构。状态监测系统基于Labview平台开发,运行于通用PC机上。实时控制系统基于Matlab/Simulink平台开发,运行于研华IPC-610L工控机上。两个系统之间通过TCP/IP进行实时通讯。利用PCL816AD卡采集由信号调理单元输出的各液压缸位移、速度、加速度及上/下腔压力信号。将伺服阀驱动信号经由PCL726DA卡输出至信号调理单元。分别利用MTS磁致位移传感器、PCB公司加速度传感器、Gems公司压力传感器采集各缸位移/速度、加速度、上/下腔压力信号。
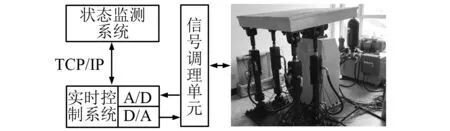
图3 实验系统示意图Fig.3 Experimental setup
基于图3系统,分别进行常值位姿分析、阶跃响应分析、加速度频率特性分析及正弦振动实验分析,检验控制系统的瞬态及稳态特性,并定量分析内力协调控制方法的效果。
表2所示为rx自由度常值位姿控制实验结果。分别采用传统的矩阵控制方法和基于运动学分析的控制方法控制平台运动,利用陀螺仪检测平台实际输出位姿。由表2可知,采用矩阵控制时,误差可达2.4%。采用运动学分析方法,误差可控制在0.22%以内。
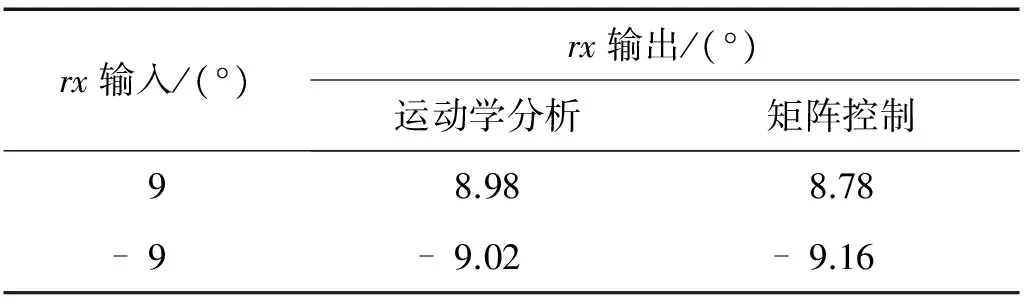
表2 常值位姿控制实验
图4所示为rx及ry两轴阶跃响应曲线。由图可知,两轴阶跃响应峰值时间约20 ms,超调量不超过15%,系统瞬态特性指标满足振动模拟实验系统要求。
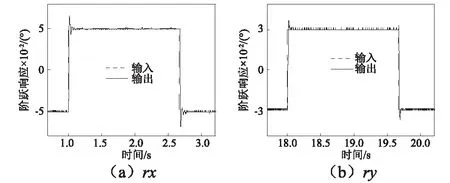
图4 阶跃响应曲线Fig.4 Step response
取5~110 Hz限带加速度随机信号作为输入指令,基于Labview/Frequency Response Function模块在线分析冗余振动台两轴的加速度频率特性,所得结果如图5所示。图中横坐标为频率,单位为Hz,纵坐标为幅频特性,单位为dB。由图可知,振动台各轴向加速度频宽均能达到100 Hz。
图6所示为ry向输入指令为200 °/s2、60 Hz时的正弦加速度跟踪曲线及各液压缸出力、冗余力曲线。由图6(a)可知,加速度响应信号存在较明显的谐波分量信号,但从幅值上看,能够实现对输入指令的跟踪。如果不采用内力协调控制,各缸出力幅值接近15 kN。采用内力协调控制后各缸出力及冗余力如图6(b)、图6(c)所示。内力协调控制明显减小了各缸间的内力耦合。
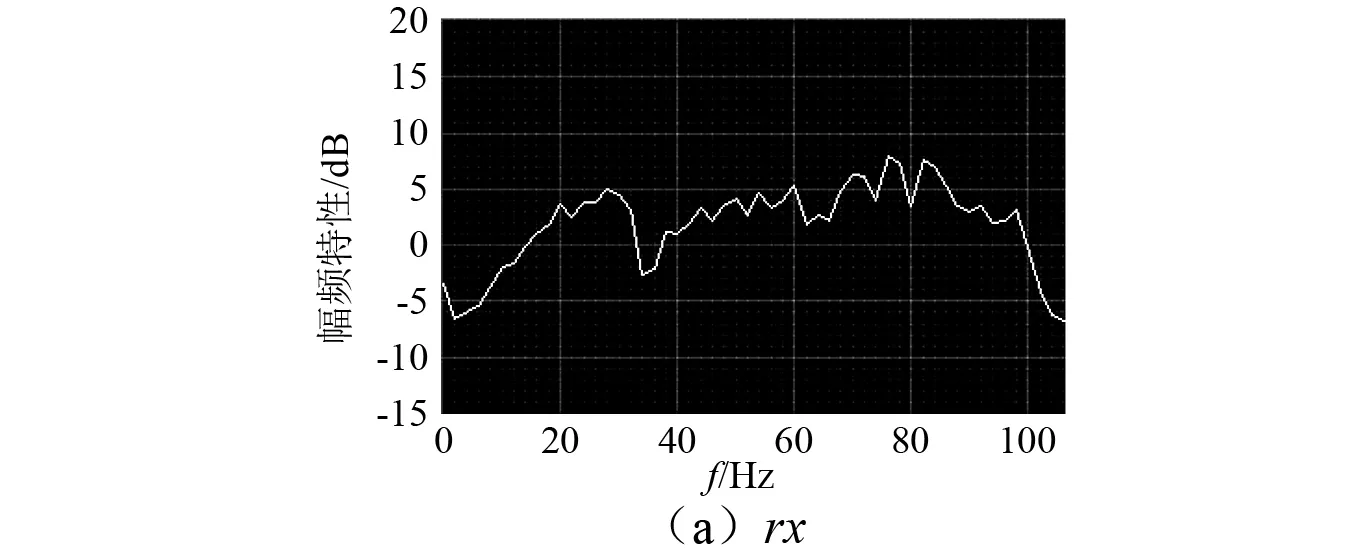
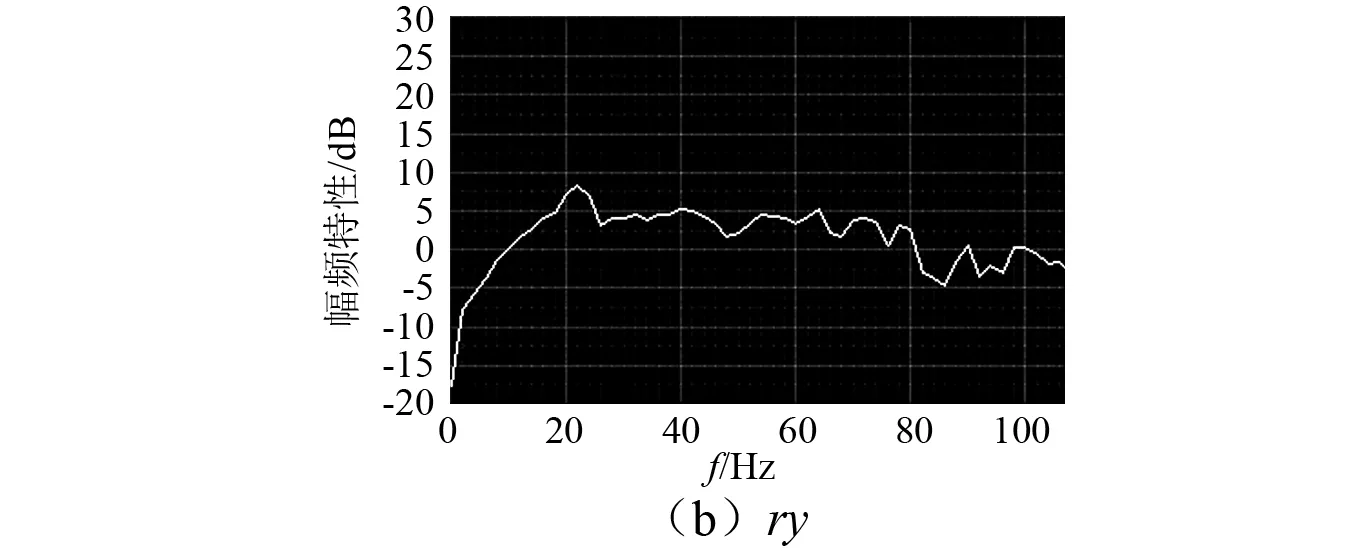
图5 加速度频率特性曲线Fig.5 Acceleration amplitude frequencyresponse characteristics of the shaking table
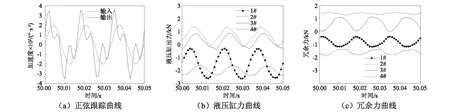
图6 正弦振动实验Fig.6 Sine vibration test
5 结 论
基于对冗余驱动振动台的运动学分析设计加速度控制回路,利用位姿正解代替传统自由度合成矩阵,提高了系统在大位姿条件下的控制精度。基于冗余振动台动力学方程,利用Jacobian矩阵计算各缸冗余力,并设计内力协调控制回路。分别通过位姿控制、阶跃响应、频率特性分析及正弦振动实验验证了控制策略的有效性。本文提出的控制策略,不仅限于角振动台控制系统。对运动学分析及内力协调控制回路进行相应变换,即可将图2所示控制方法推广应用于三轴、六轴等多轴冗余驱动电液振动台。
由图6(a)可知,正弦振动实验中加速度响应信号存在较明显的2次及3次谐波分量,波形失真较大。但图6(b)的液压缸力曲线中相应频率的谐波分量并不明显。分析加速度谐波产生原因,提高正弦振动跟踪精度将是后期工作的主要内容。
[ 1 ] 陈章位, 于慧君. 振动控制技术现状与进展[J]. 振动与冲击, 2009, 28(3): 73-77.
CHEN Zhangwei, YU Huijun. Existing state and development of vibration control technology[J]. Journal of Vibration and Shock, 2009, 28(3): 73-77.
[ 2 ] 闫磊, 李青宁, 尹俊红, 等. 多维地震激励下人字形桥梁地震模拟振动台试验研究[J]. 振动与冲击, 2016, 35(7): 167-176.
YAN Lei, LI Qingning, YIN Junhong, et al. Shaking table tests for Y-shaped bridges under multi-dimensional seismic excitation[J]. Journal of Vibration and Shock, 2016, 35(7): 167-176.
[ 3 ] 高春华, 纪金豹, 闫维明, 等. 地震模拟振动台技术在中国的发展[J]. 土木工程学报, 2014, 47(8): 9-19.
GAO Chunhua, JI Jinbao, YAN Weiming, et al.Developments of shaking table technology in China[J]. China Civil Engineering Journal, 2014, 47(8): 9-19.
[ 4 ] 鲁亮, 江乐, 李鸿, 等. 柱端铰型受控摇摆式钢筋混凝土框架抗震性能的振动台试验研究[J]. 振动与冲击, 2016, 35(4): 193-198.
LU Liang, JIANG Le, LI Hong, et al. Shaking table tests for a seismic performance of a controllable rocking reinforced concrete frame with column-end-hinge joints[J]. Journal of Vibration and Shock, 2016, 35(4): 193-198.
[ 5 ] TOMA I O, ATANASIU G M. Modern trends in experimental earthquake engineering research[J]. The Bulletin of the Polytechnic Institute of Jassy, Construction. Architecture Section, 2010, 56(4): 43.
[ 6 ] 许维炳, 闫维明, 王瑾, 等. 调频型颗粒阻尼器与高架连续梁桥减震控制研究[J]. 振动与冲击, 2013, 32(23): 94-99.
XU Weibing, YAN Weiming, WANG Jin, et al. A tuned particle damper and its application in seismic control of continuous viaducts [J]. Journal of Vibration and Shock, 2013, 32(23): 94-99.
[ 7 ] TAGAWA Y, KAJIWARA K. Controller development for the E-Defense shaking table[J]. Journal of Systems and Control Engineering, 2007, 221: 171-181.
[ 8 ] 沈刚, 朱真才, 李翔, 等. 三轴六自由度电液振动台解耦控制[J]. 振动与冲击, 2015, 34(19): 1-7.
SHEN Gang, ZHU Zhencai, LI Xiang, et al. Decoupling control for a triaxial 6-DOF Electro-hydraulic shaking table[J]. Journal of Vibration and Shock, 2015, 34(19): 1-7.
[ 9 ] PLUMMER A R. Motion control for overconstrained parallel servohydraulic mechanisms[C]∥The 10th Scandinavian International Conference on Fluid Power. Tampere: SICFP, 2007: 1-13.
[10] UNDERWOOD M A , KELLER T. Applying coordinate transformations to multi degree of freedom shaker control[J]. Sound and Vibration, 2006, 40(1): 22-27.
[11] 关广丰. 液压驱动六自由度振动试验系统控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.
[12] CHENG H, YIU Y K, LI Z. Dynamics and control of redundantly actuated parallel manipulators[J]. IEEE/ASME Transactions on Mechatronics, 2003, 8(4): 483-491.
[13] MÜLLER A, HUFNAGEL T. Model-based control of redundantly actuated parallel manipulators in redundant coordinates[J]. Robotics and Autonomous Systems, 2012, 60(4): 563-571.
[14] 张连朋, 杨炽夫, 杨志东, 等. 冗余驱动液驱振动台台阵系统内力分析及其抑制方法研究[J].振动与冲击, 2017, 36(3): 83-92.
ZHANG Lianpeng, YANG Chifu, YANG Zhidong, et al. Inner coupling force analysis and suppression for redundant-drive hydraulic shaking tables[J]. Journal of Vibration and Shock, 2017, 36(3): 83-92.
[15] PLUMMER A R. A general co-ordinate transformation framework for multi-axis motion control with applications in the testing industry[J]. Control Engineering Practice, 2007, 18(6): 598-607.
[16] 何景峰, 李保平, 佟志忠, 等. 液压驱动冗余振动台自由度控制及内力协调[J]. 振动与冲击, 2011, 30(3): 74-
78.
HE Jingfeng, LI Baoping, TONG Zhizhong, et al. DoF control and inner force balancing of hydraulically redundant actuated shaking table[J]. Journal of Vibration and Shock, 2011, 30(3): 74-78.
[17] MERLET J P. Parallel robots[M]. Springer Science & Business Media, 2012.
[18] KOEKEBAKKER S H. Model based control of a flight simulator motion system[D]. Delft: Delft University of Technology, 2001.
[19] JIANG H Z, HE J F, TONG Z Z. Modal space control for a hydraulically driven stewart platform[J]. Journal of Control Engineering and Technology, 2012, 2(3): 106-115.
[20] 付云贵. 冗余驱动电液振动台运动学分析及内力协调控制方法研究[D]. 大连: 大连海事大学, 2017.

