移动边缘计算任务卸载和基站关联协同决策问题研究

于博文 蒲凌君,2 谢玉婷 徐敬东 张建忠

1(南开大学计算机与控制工程学院 天津 300071) 2 (广东省大数据分析与处理重点实验室(中山大学) 广州 510006) (bowenyu@mail.nankai.edu.cn)

随着无线通信技术的发展以及传感器种类的丰富，诸如智能汽车、手机等IoT设备可以通过蜂窝网络、低功耗广域网等方式接入互联网，并能使用装备的传感器感知周围环境的状态.在这一背景下，众多IoT应用应运而生，例如群智感知、智能监控、车联网应用等.在这类应用中，IoT设备会周期性地采集指定的数据，本地处理或上传到云端服务器进行分析，产生相应知识或模式，为人们的生活和工作提供便利.随着IoT应用的类型不断丰富、功能日益强大，它们对计算能力和响应延时提出了更高的要求.例如在车联网和增强现实等领域，这些应用要求实时处理采集到的视频信息并将结果反馈给用户.大量的密集型计算任务势必会加快IoT设备的能源消耗，缩短其使用寿命.目前，IoT设备与云端相结合是IoT应用的主要模式.然而IoT设备和远程云平台间长距离通信存在网络传输延时不稳定的问题，这将会导致IoT应用的延时过长，无法满足对延时有明确要求的应用.

作为一种很有前景的解决方案，移动边缘计算能够有效地解决传统移动云计算的不足.移动网络运营商和云服务提供商以合作的形式在网络边缘提供丰富的通信和计算资源，IoT设备可以通过高速无线接入网络在蜂窝网络边缘近距离地获取所需的计算资源和服务[1-2].随着万物互联和大数据时代的到来，IoT设备的数量和移动数据流量得到了飞速提升.根据Cisco的报告[3]，移动数据流量将在未来的5年中增长7倍，到2021年将达到每月49艾字节(exabyte，EB)(1 EB=106TB)，同时全球IoT设备数量将从目前的80亿增长到120亿.这将使其接入网络获取移动边缘服务器的计算资源变得困难.目前的网络架构将很难应对未来大规模设备接入网络的需求.为应对海量的设备连接和数据流量，5G架构下的多基站协作服务场景如超密集网络(ultra-dense networks， UDN)逐渐成为移动网络运营商广泛接受的模式[4-5].在UDN网络中，移动网络运营商会部署大量微基站和宏基站为移动设备提供接入服务，这必然会导致蜂窝网络的能耗显著提升，使运营成本大幅度提高.因此如何降低UDN网络的能耗是目前蜂窝网络研究关注的核心问题[6].本文希望通过对IoT设备的计算卸载、设备-基站关联以及基站睡眠的合理调度，提高IoT设备的计算能力，同时尽可能减少IoT设备和蜂窝基站的能源开销.

结合5G的移动边缘计算的能耗问题近年来得到了工业界和学术界的广泛关注[7-10].文献[11-13]研究了多设备的计算卸载的最优能耗问题.文献[14-16]对计算卸载与移动边缘服务器资源联合调度展开了研究，解决了移动设备和服务器整体能耗或能源效率最优化的问题.然而这些研究工作通常只考虑单一基站(即宏基站)为IoT设备提供接入服务，没有解决未来5G环境下的多基站协作服务场景下的IoT设备、基站和边缘服务器联合调度的问题.

本文提出了一个基于超密集网络的移动边缘计算框架(computing offloading framework based on MEC and UDN, COMED).与以往研究工作不同的是:COMED框架实现了超密集网络中高效的计算卸载、基站睡眠以及IoT设备-基站关联三者的调度.框架的示意图如图1所示，其中包括IoT设备、微基站、宏基站以及边缘服务器.IoT设备通过自身的传感器采集数据.宏基站负责调度IoT设备与最合适的基站进行关联并令没有关联IoT设备的基站进入睡眠状态以节约能量；同时负责调度IoT设备本地处理任务或将任务卸载到边缘服务器上进行处理.服务器根据定制的服务计划为IoT设备上传的任务分配计算资源.当IoT设备的任务在本地或边缘服务器上处理完毕之后，结果将会被传送到互联网上.例如车联网应用中的危险预警系统需要使用高清摄像头、超声波和激光雷达周期性地采集道路上的视频和数据信息，分析当前道路上是否存在异常状况，进而为人们的生命财产安全提供保障.在COMED框架中，车辆可以本地处理采集到的视频和数据，也可以通过相关调度利用移动边缘计算提供的丰富的计算资源处理任务.为了让COMED框架在实际中能够对IoT应用提供高效的计算卸载支持，它需要满足3个要求：

1) COMED框架需要在保证IoT应用的服务质量(如延时)的前提下尽可能做到高效节能.降低IoT设备和基站的能源消耗，对延长IoT设备的使用寿命、提高设备和基站的能源利用率具有十分重要的现实意义.

2) COMED框架需要在线运行.由于蜂窝网络状态、IoT设备移动性以及边缘云可用资源均随时间动态变化，准确预测未来系统信息比较困难，因此这就要求COMED框架能够仅使用当前系统信息进行任务卸载、基站开关和设备-基站关联决策.

3) COMED框架需要具有可伸缩性.由于在城市环境中会部署大规模的IoT设备，因此要求COMED框架设计的任务卸载、基站开关和关联决策具有较低时间复杂度，从而能为更多的设备和应用提供服务.

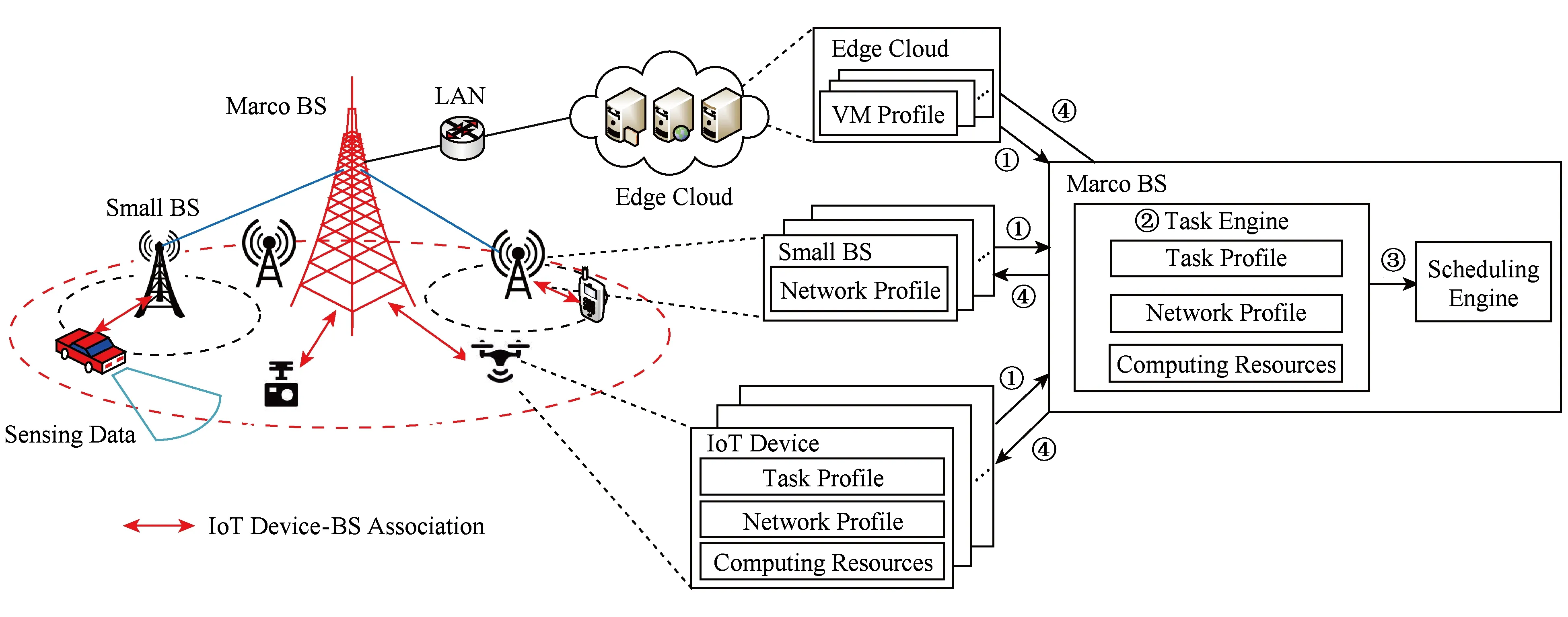
Fig. 1 The framework of task offloading for COMED图1 COMED任务卸载框架示意图

基于上述要求，本文首先对COMED框架进行系统建模，包括IoT设备资源模型、边缘服务器模型、IoT应用和负载排队模型、设备和基站能耗模型等.在此基础上，本文提出并形式化了一个针对全网络的任务负载调度、IoT设备-基站关联以及基站睡眠调度的联合任务卸载问题，旨在最小化时间平均意义下COMED框架的能耗(即IoT设备和基站的能耗之和)，同时兼顾应用任务的延时要求(第2节).针对优化问题，本文根据李雅普诺夫优化理论提出了联合计算卸载、基站睡眠和用户-基站关联(joint computing offloading,BS sleeping and user-BS assoication, JOSA)的在线任务卸载算法.作为该算法的核心模块，本文提出了一个基于松弛-对偶理论的SlotCtrl算法，该算法仅根据当前时间片内的系统信息进行调度.通过数学证明可知，本文提出的在线JOSA算法与线下理论最优算法的节能效果十分接近(第3节).大量模拟实验结果不但证实了理论分析结果，而且与设备本地处理相比，系统整体节能30%以上(第4节).

1 相关工作

为了节约IoT设备的能量，同时有效地利用边缘服务器的计算资源，近年来许多研究者开展了针对移动边缘计算中计算卸载与服务器资源联合调度问题的研究.其中，文献[14]将移动边缘计算与无线充电技术相结合，研究了可无线充电的IoT设备的计算卸载问题，提出了基于李雅普诺夫优化的在线调度策略;文献[15]假设云端服务器为每个IoT设备分配一台虚拟机，研究了多设备任务卸载开销最小化的问题，提出了高效的资源分配策略;文献[16]研究了车载云计算场景中最大化数据传输和计算的能源效率问题，在最小的传输率、最大的延时和时延抖动的情况下，满足应用的服务质量要求;文献[17]假设IoT设备共享有限的无线带宽和服务器资源，研究了同时满足无线带宽和服务器资源限制条件下最大化计算卸载执行收益的优化问题.通过对问题进行解耦分析，该文提出了高效的设备无线传输功率设置及服务器资源分配策略.然而上述这些研究工作只针对单一蜂窝基站场景，难以适用于未来5G架构下的UDN网络.

针对UDN网络的移动边缘计算卸载问题，文献[18]开展了基于MIMO的多蜂窝基站场景下多设备任务执行能耗最小化的研究；文献[19]解决了C-RAN网络架构中多设备任务执行能耗最小化问题.然而这些工作只关注设备任务执行能耗最优，并没有涉及5G架构下蜂窝基站睡眠、设备与蜂窝基站关联[20]等关键问题.

在这些研究的基础上，本文重点研究了5G超密集网络中移动边缘计算的计算卸载、IoT设备-基站关联及基站睡眠调度的联合优化问题，提出了IoT设备与基站能源最优的调度方案，同时保证了任务的延迟约束.

2 系统模型与问题形式化

本文提出的COMED框架如图1所示，其中包括一个基站集合M={1,2,…,m}和一个IoT设备集合N={1,2,…,n}.在基站集合M中存在一个宏基站以及m-1个微基站.IoT设备可以通过无线网络接入基站，获得处于边缘云服务器的资源.IoT设备的任务可以通过调度，本地执行或卸载到边缘云服务器上执行.本文考虑框架内的每个IoT设备用户在边缘云服务提供商处购买计算资源，用来处理IoT设备卸载到边缘云的任务.

类似于UDN以宏基站作为小型基站和微基站的控制器，本文将宏基站作为COMED框架的中央控制器对系统中的任务卸载、基站睡眠以及设备-基站关联进行调度，在宏基站中执行一个任务引擎进程.任务引擎负责收集IoT设备本地及边缘服务器端待完成的任务信息、计算资源信息以及IoT设备和基站的网络状况信息.这些信息可以用于估计当前任务在每个IoT设备和边缘服务器上的执行时间和能耗，对于框架的调度至关重要.COMED需要访问这些配置文件，以便更好地对任务卸载、基站睡眠以及设备-基站关联进行调度.

本文考虑COMED框架以时间片为单位运行.单位时间片t∈{1,2,3,…}的长度由IoT应用的服务提供商决定.对每个时间片，IoT设备和边缘服务器需要向宏基站提供当前未完成的任务量和可用的计算资源，IoT设备和基站需要提供当前的网络状况(如图1步骤①).宏基站收到当前任务量和网络状况后，由任务引擎构建完整的任务信息、网络信息以及计算资源信息(如图1步骤②).这些信息将用于决定任务卸载、基站睡眠以及设备-基站关联的调度.接下来，任务引擎将启动一个负责当前时间片任务卸载、基站睡眠以及设备-基站关联调度的调度器(如图1步骤③).调度器利用当前时间片的任务信息、网络信息以及计算资源信息来估计如何更好地对任务卸载、基站睡眠以及设备-基站关联进行调度.为此，调度引擎需要确定调度策略.目前COMED使用在满足任务平均延时的前提下尽可能降低执行任务能耗的策略.在调度器计算得到该时间片的调度结果之后，调度结果会通过网络传给IoT设备、基站和边缘服务器(如图1步骤④).任务引擎会通知IoT设备关联到哪个基站、本地执行和卸载到边缘服务器的任务量；通知基站是否开启以及关联哪些IoT设备；通知边缘服务器为相应IoT设备的虚拟机提供服务.

2.1 IoT设备资源模型

本文假设IoT设备搭载单核CPU，按照FIFO顺序处理IoT应用的任务.目前主流处理器有许多不同的工作模式，比如根据工作负载通过动态电压频率调节CPU频率(DVFS)的按需模式、以最高CPU频率运行的性能模式以及以最低CPU频率运行的节能模式等.令si(t)为单位时间片IoT设备i的CPU周期数，其值可通过稳定CPU工作频率得到[21].令pi(si(t))为CPU单位时间片周期数所对应的功率.

定义0-1控制变量ai j(t)为IoT设备-基站关联变量.当ai j(t)=1时表示IoT设备i与基站j关联；否则ai j(t)=0.对于IoT设备i，本文定义其上传功率为pi.当IoT设备i与基站j关联时，IoT设备i与基站j的上行链路SINRΓi j(t)可以通过IoT设备i以及i周围的其他IoT设备的上行传输链路的准静态衰落信道增益预估得到.本文假设IoT设备只有在当前上行链路SINRΓi j(t)大于目标SINRγi j时才能与相应的基站建立关联.对于给定的IoT设备i的上行链路SINRΓi j(t)，如果不等式Γi j(t)≥γi j成立，本文将IoT设备i与基站j的上传链路的速度定义为[19,22]

ri j=Blog(1+γi j),

其中,B为链路带宽.

对于IoT设备的传输模型，有约束条件：

(1)

(2)

(3)

式(1)表示每个IoT设备在同一时间片至多与1个基站进行关联；式(2)表示对于任意基站j，同一时刻最多可关联hj个IoT设备；式(3)表示IoT设备i只有在上行链路SINRΓi j(t)大于目标SINRγi j时才能与基站j建立关联.此外为了方便起见，本文定义IoT设备i在时间片t的上传速度为

出于对IoT设备的安全和隐私考虑，本文不考虑宏基站对IoT设备的CPU频率进行控制.同时为了不增加现有蜂窝网络调度的开销，本文不考虑控制IoT设备的上传功率.为方便读者阅读，本文只对问题的约束条件以及重要的公式加以编号.

① 本节只考虑了IoT设备和基站的能耗，对于边缘服务器能耗在3.2节中讨论.

2.2 边缘服务器模型

本文考虑每个IoT设备的用户分别在边缘云服务提供商处购买一台特定的虚拟机.虚拟机每个时间片的计算能力为vi.令0-1控制变量ci(t)表示在时间片t边缘云是否为虚拟机i分配相应的计算资源.如果ci(t)=1，表示边缘云在时间片t为虚拟机i分配计算资源；否则ci(t)=0.边缘云每个时间片分配的计算资源不能超过服务器的物理资源vmax(t)，即存在约束条件:

(4)

2.3 任务模型

本文考虑如下类型的IoT设备应用：应用按照一定频率周期性使用IoT设备的传感器采集信息，并进行处理分析.通常，此类应用的任务被要求在一定延时内处理完毕，如车载计算中绿灯最优速度建议应用、蜂窝IoT应用以及通过IoT设备收集数据的Crowdsourcing应用等.与许多现有工作相同[13,16,23]，COMED框架关注于对IoT应用本地执行与卸载执行的任务工作量调度.

1) 任务模型.在每个时间片t，移动节点i会生成ki(t)比特的任务.本文假设任务的平均到来量为λ，其值可以通过离线统计得到.CPU处理任务需要消耗一定的CPU计算资源.定义任务的处理密度为ρ，即处理1 b任务需要ρ个CPU运行周期.例如识别高清视频一帧中的某一种物体(如车辆、障碍物或行人等)大约需要9.6×104个CPU周期，其任务处理密度大约为50CPU cycles/b[24].

2) 任务队列模型.本文引入任务队列来描述当前IoT设备和边缘服务器中尚未处理的任务量.定义Qi(t)为IoT设备i的任务队列，其值为IoT设备i在时间片t时的本地任务残余量.Qi(t)在下一个时间片的更新规则：

Qi(t+1)=Qi(t)+ki(t)-xi(t)-yi(t),

其中，控制变量xi(t)为时间片t时的本地任务执行量，控制变量yi(t)为时间片t时的卸载任务量.这里包含约束条件：

xi(t)≤si(t)/ρ,

(5)

yi(t)≤ri(t),

(6)

xi(t)+yi(t)≤Qi(t)+ki(t).

(7)

式(5)表示IoT设备每个时间片本地处理的任务量不能超过其计算能力；式(6)表示IoT设备每个时间片卸载的任务量不能超过其传输能力；式(7)表示IoT设备每个时间片本地处理的任务量和卸载的任务量之和不能超过其任务队列中的任务残余量.

定义Li(t)为IoT设备i在边缘云虚拟机的任务队列，其值为虚拟机i在时间片t时的任务残余量.Li(t)在下个时间片的更新规则为

Li(t+1)=Li(t)+yi(t)-ci(t) min (vi/ρ,Li(t)),

其中,ci(t) min (vi/ρ,Li(t))表示虚拟机i在一个时间片内处理的任务量.

2.4 能耗模型

在COMED框架中，本文考虑的能耗包括IoT设备和基站的能耗①.在IoT设备的能耗模型中，IoT设备能耗由本地计算的能耗和卸载任务的能耗组成.本文假设IoT设备本地计算与卸载任务产生的能耗分别与其计算和传输的时间成正比.因此IoT设备的能耗可以表示ei(t)为

等式右侧前一部分为IoT设备i本地处理xi(t)比特任务的能耗，后一部分为卸载yi(t)比特任务的能耗.

基站的功耗可由一个基础功耗加一个动态功耗表示[25].为了方便起见，本文将基站的功耗Pj定义为其基础功耗的β倍，β可通过对基站能耗的统计得到.在UDN中基站可以通过睡眠调度节省能量.本文定义0-1控制变量bj(t)为基站睡眠调度变量.当bj(t)=1时，表示基站j处于工作模式；否则bj(t)=0.框架内作为调度服务器的宏基站需要一直处于工作状态.基站j的能耗可表示为

Ej(t)=bj(t)Pj.

0-1控制变量bj(t)有约束条件：

ai j(t)≤bj(t),

(8)

即IoT设备i只有在基站j处于工作模式时，才能与j进行关联.

2.5 延 时

IoT设备在运行应用时，通过传感器采集到的数据应在有限的延时dmax内被执行.为了满足应用的延时要求，同时考虑未来5G网络环境下大规模的IoT设备，根据利特尔法则[26]，本文定义在全局意义上的任务平均延时为

(9)

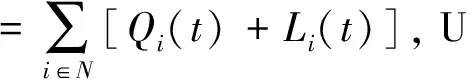
根据任务队列模型，通过迭代可以得到:

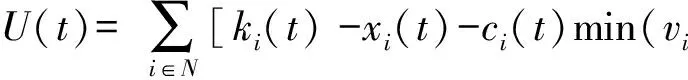
2.6 问题形式化

本文通过对IoT设备任务、基站资源以及边缘服务器资源的分配，旨在最小化系统整体的能量开销，同时从长远角度满足应用的平均延时.本文制定出优化问题：

s.t. 式(1)～(9)成立.

3 算法设计

李雅普诺夫优化[27]对于解决具有时间平均意义下的目标函数和约束条件的优化问题是非常有效的.通过调用李雅普诺夫drift-plus-penalty方法，本文设计了一个利用每个时间片当前系统信息的任务卸载、基站睡眠和IoT设备-基站关联调度的在线算法JOSA对问题P进行求解.

3.1 问题转化

为了满足应用延时的约束条件，本文引入虚队列B：

B(t+1)=[B(t)-nλdmax]++U(t),

其中,[x]+=max(0,x)，U(t)为虚队列B每个时间片的任务到来量，nλdmax为相应的离开量.虚队列B用来描述当前系统整体待完成任务的堆积情况.本文规定虚队列B的初始值为0.

本文采用李雅普诺夫优化框架对目标函数进行优化，同时保证虚队列和实队列的稳定性.定义如下的二次李雅普诺夫方程：

其中,向量Θ(t)=[Q1(t),Q2(t),…,Qn(t),L1(t),L2(t),…,Ln(t),B(t)]T为框架中所有队列的剩余量.本文定义每个时间片的drift-plus-penalty方程为

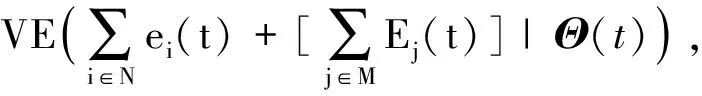
其中,ΔY(Θ(t))=E[Y(Θ(t+1))-Y(Θ(t))]，V是目标函数最优性和队列稳定性之间的权衡参数.根据李雅普诺夫drift-plus-penalty方程，本文将问题P转化为

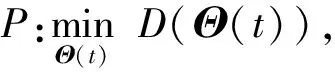
s.t. 式(1)～式(8)成立.

因为新的目标函数包含难以解决的二次项，所以本文将在最小化引理1中给出目标函数的上限(即下面引理1中式(10)的右边).

引理1. 对于任意Θ(t)，李雅普诺夫drift-plus-penalty方程D(Θ(t))满足：

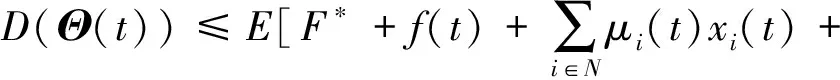
(10)

其中:

F*是常量，f(t)是不包含控制变量的部分.

证明. 根据Qi和Li(t)的更新规则，可以得到

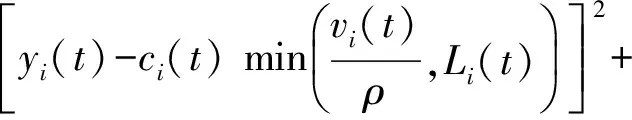
根据B(t)的更新规则以及事实([a-b]++c)2≤a2+b2+c2+2a(c-b)可以得到:

B(t+1)2≤B(t)2+(Nλdmax)2+U(t)2+
2B(t)[U(t)-Nλdmax].

将上述等式和不等式代入李雅普诺夫drift-plus-penalty方程D(Θ(t))可以得到:

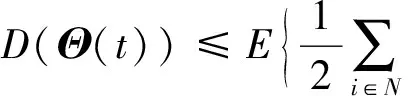
整理得到:

其中:

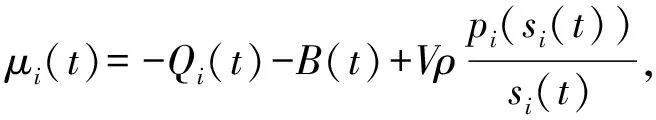
我们假设ki(t)≤kmax,xi(t)≤xmax,yi(t)≤ymax,min(vi/ρ,Li(t))≤zmax，整理得到:

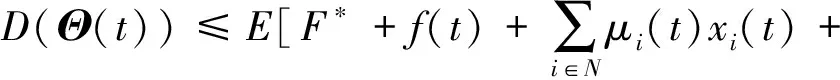
其中:

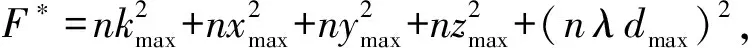
证毕.

由于F*是常量，f(t)中不包含控制变量，因此本文在求解drift-plus-penalty方程D(Θ(t))上界的过程中不考虑F*和f(t).那么最小化drift-plus-penalty方程D(Θ(t))上界的问题可以表示为

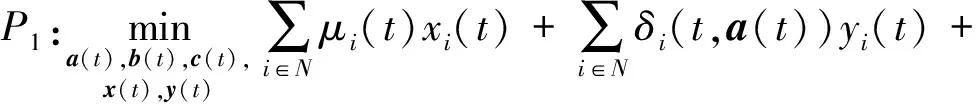
s.t. 式(1)～(8)成立.

在此情况下，最小化drift-plus-penalty方程D(Θ(t))的上限能使原问题P有良好的表现是可以被证明的(见3.5节定理1).

3.2 JOSA算法

本文提出一个在线算法JOSA用来最小化drift-plus-penalty方程D(Θ(t))的上限.

1) 找到每个IoT设备中的任务队列的最佳工作负载分配、IoT设备-基站关联以及基站睡眠调度：

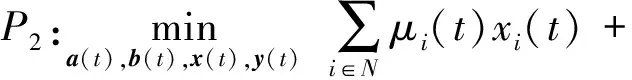
s.t. 式(1)～(3)，式(5)～(8)成立.

2) 找到边缘服务器资源的最佳分配：

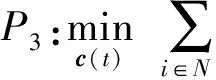
s.t. 式(4)成立.

3) 根据步骤1和步骤2的结果，更新框架中的实队列和虚队列.

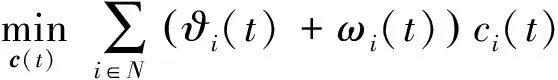
3.3 求解P2的SlotCtrl算法实现

问题P2是在线优化算法JOSA需要求解的核心问题.P2的控制变量中包含2个0-1整数变量和2个连续变量，因此P2是典型的混合整数规划问题，通常是NP难问题.为了能够高效地对P2进行求解，本文提出了一个基于松弛-对偶理论的SlotCtrl算法作为在线优化算法JOSA的核心模块.其核心思路如图2所示.首先算法将P2中的0-1整数控制变量松弛至[0,1]，使问题转化为P4.其次通过给定控制变量b(t)，x(t)和y(t)，将P4转化为P5.问题P5是一个较难求解的分数规划问题，因此算法引入与P5具有相同最优解的线性规划(LP)问题P6.通过引入拉格朗日乘子得到P6的对偶问题Dual-P6，并使用次梯度法获得对偶问题的优化方案.在给定引入拉格朗日乘子的前提下，求解LP问题P7得到a(t).在此基础上，SlotCtrl算法使用次梯度法对控制变量b(t)和y(t)进行优化，即P8.求解LP问题P9得到x(t).最后算法通过迭代(P5至P9)，直至控制变量a(t),b(t)，x(t)和y(t)收敛，得到问题P4的最优解.通过分析，可以证明经由上述步骤得到的问题P4的解是整数解，即P2与P4具有相同的最优解.

Fig. 2 Schematic diagram of SlotCtrl algorithm图2 SlotCtrl算法流程示意图

1) 松弛0-1整数控制变量a(t)和b(t).

通过将变量ai j(t)和bj(t)松弛至[0,1]，P2转化为P4.

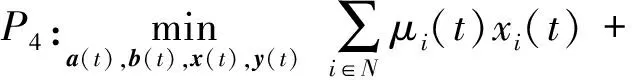
s.t. 式(1)～(3)、式(5)～(8)成立，且0≤ai j(t),bj(t)≤1.

在P4目标函数的第2项中，包含控制变量ai j(t)的分数与控制变量yi(t)相乘的部分.同时在P4的约束条件式(6)中，ai j(t)和yi(t)也耦合在一起.这使问题P4很难直接求解.因此本文将P4分解为2个子问题：首先，对于给定的控制变量b(t)，x(t)和y(t)，对P4进行求解(问题P5～P9)；然后根据之前的结果，使用次梯度法对b(t)和y(t)进行优化(问题P8)，最后求解LP问题P9得到x(t).

2) 对于给定的b(t)，x(t)和y(t)，求解P4.

通过给定b(t)，x(t)和y(t)，P4转化为问题P5.

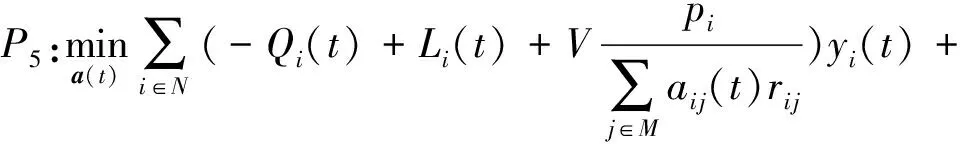
s.t. 式(1)～(3)、式(6)、式(8)成立，且0≤ai j(t)≤1.

P5是关于控制变量a(t)的分数规划.由于其目标函数中除了ai j(t)之外的参数都是定值且ai j(t)只存在于目标函数第1项的分母部分，因此可以通过求解与P5具有相同最优解的LP问题P6获得P5的最优解.

s.t. 式(1)～(3)、式(6)、式(8)成立，且0≤ai j(t)≤1.

通过引入拉格朗日乘子θ和φ，可以得到P6的对偶问题Dual-P6.

其中:

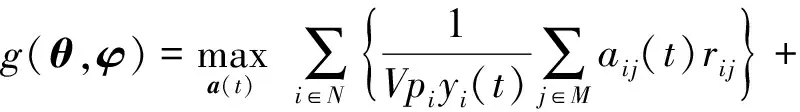
(11)

Dual-P6的优化方案可以通过次梯度法获得[28]:

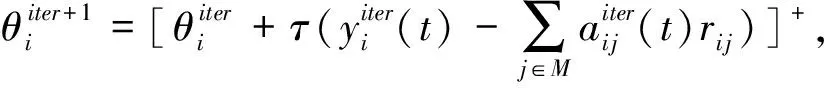
(12)

其中,τ为每次迭代的步长，iter为迭代次数.

通过给定θ,φ,b(t)和y(t)，最大化式(11)是一个标准的LP问题，可以表示为

P7:g(θ,φ)

s.t. 式(1)～(3)成立，且0≤ai j(t)≤1.

P7可以通过单纯形法等算法有效地进行求解.虽然ai j(t)被松弛为0～1的小数，但通过P7求得的ai j(t)中的最优解仍然是整数.这部分的证明详见本节引理2的证明.

3) 优化b(t)，x(t)和y(t).

由于问题P6的目标函数和约束条件都是线性的，因此P6是一个凸优化问题.同时，由于P6是具有线性约束条件的LP问题，因此P6满足Slater条件.根据Slater定理，P6具有强对偶性，P6和其对偶问题Dual-P6的对偶间隙为0.

令f(a(t))为在给定a(t)的前提下，问题P6的目标函数.b(t)和y(t)的优化可以通过求解问题P8得到:

P8可以通过次梯度法求解:

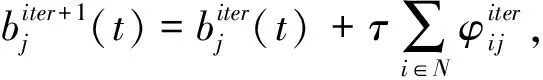
(13)

令f′(a(t),b(t),y(t))为在给定a(t),b(t),y(t)的前提下，问题P5的目标函数.x(t)的优化可以通过求解问题P9得到:

s.t. 式(5)、式(7)成立.

问题P9是一个标准的LP问题，可以通过单纯形法等算法有效地进行求解.

算法1. SlotCtrl算法.

输入：框架中所有队列的剩余量Θ(t)；

输出：a(t)，b(t)，x(t)和y(t).

① 初始化θ，φ，a(t)，b(t)，x(t)和y(t)；

② do{

③ do{

④ 用LP solver求解P7得到a(t)；

⑤ 根据式(12)更新θ和φ；}

⑥ while(P7的目标函数最大值未收敛)；

⑦ 根据式(13)更新b(t)和y(t)；

⑧ 用LP solver求解P9得到x(t)}

⑨ while (P5的目标函数最小值未收敛)；

4) SlotCtrl算法分析

性质1. 令A为完全单模矩阵，b为整数向量，则多面体P{x|Ax≤b}的顶点为整数[29].

性质2. 如果一个LP问题具有最优解，则至少有一个最优解在由约束条件定义的多面体的顶点处[30].

引理2.P7的最优解是整数解.

证明. 为了分析P7的性质，本文定义一个新向量a′(t)，a′(t)将a(t)中所有的列整合在一起：

a′(t)=[a1,1(t),a1,2(t),…,a1,m(t),a2,1(t),
a2,2(t),…,a2,m(t),…,an,1(t),
an,2(t),…,an,m(t)]T.

然后将P7改写为标准形式:

s.t.Aa′(t)≤b，

其中,约束矩阵A和向量b为

b≐[h1,h2,…,hm,1,1,…,1]T.

显然向量b是一个整数向量.本文需要证明约束矩阵A为完全单模矩阵.将矩阵A分块:

其中,Wj∈M是m×n的矩阵，其第j行元素全为1，其余元素全为0；Ij∈M是n×n的单位矩阵.令Gk为约束矩阵A的任意k×k的子方阵，det(Gk)为Gk的行列式的值.当k=1时，det(Gk)={0,1}.当k≥2时，会有2种情况：

情况1.Gk是Wj,Ij或0的子方阵.如果Gk是Wj的子方阵，由于Gk至少有一行元素全为0，因此det(Gk)=0.如果Gk是Ij的子方阵，由于Ij是单位矩阵，因此det(Gk)={0,1}.

如果Δv*=0，则第v*列的元素全为0，因此det(Gk)=0.

如果Δv*=1，则det(Gk)=det(Gk-1)={0,±1}.

如果Δv*=2，则Gk的每列都正好有2个元素为1，其中一个来自Wj,另一个来自Ij.由于Wj和Ij中元素1的个数相等，因此可以通过变化使Gk的一行全为0.因此det(Gk)=0.

所以，约束矩阵A的任意子方阵的行列式值为0或1.根据完全单模矩阵的定义，约束矩阵A为完全单模矩阵.最后，通过性质1和性质2可以得到P7的最优解一定是整数解.

证毕.

引理3. 算法1的结果是P2的最优解.

证明. 根据引理2可以得到对于任意可行的b(t)，x(t),y(t),θ和φ，P4的最优解中控制变量ai j(t)是取值为0或1的整数.因此通过算法1得到的最优解中，ai j(t)也是取值为0或1的整数.

对于b(t)，根据约束式(8)，即ai j(t) ≤bj(t)，如果存在任意i使得ai j(t)=1，则bj(t)=1.而如果∀i∈N，ai j(t)=0，则相应的bj(t)=0.这是因为P4的目标函数中bj(t)的系数σj(t)是非负的.

综上所述，根据算法1求得的最优解中，ai j(t)和bj(t)都是取值为0或1的整数，可以确定算法1的最优解即为P2的最优解.

证毕.

3.4 求解P3的算法实现

P3是一个0-1整数规划问题，可以通过与P2类似的方法进行求解.本文将P3中的0-1控制变量c(t)松弛至[0,1]，则P3转化为P10.

s.t. 式(4)成立，且0≤ci(t)≤1.

通过引入拉格朗日乘子η，可以得到P10的对偶问题Dual-P10.

其中:

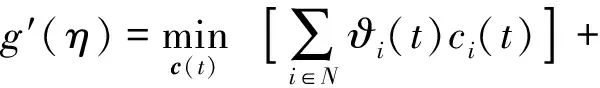
(14)

Dual-P10的优化方案可以通过次梯度法获得:

其中,τ为每次迭代的步长，iter为迭代次数.通过给定η，最大化式(14)是一个标准的LP问题，可以表示为

P11:g′(η)，

s.t. 式(4)成立，且0≤ci(t)≤1.

证明c(t)的最优解为整数的过程与引理2相同.

3.5 性能分析

定理1表明框架在时间平均意义下的最小能耗期望值的范围，以及框架内实队列和虚队列剩余量在时间平均意义下的积压范围.

定理1. 对于任意IoT设备i，假设平均工作负载到来量λi严格在系统处理能力范围内(例如λi+ε≤Ω)，那么可以通过推导得到:

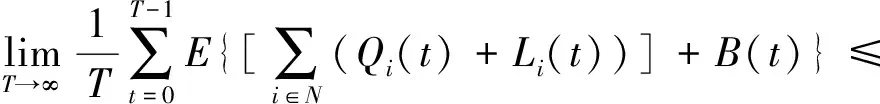
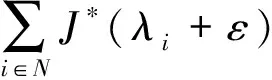
证明. 设通过离线优化得到的最佳调度策略为Φ*(t)={x*(t),y*(t),a*(t),b*(t),c*(t))，它满足:

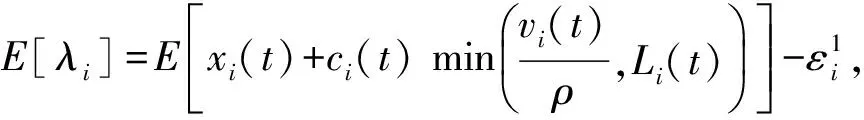
首先证明平均队列的上限.由于JOSA算法可以得到每个时间片的最优解，因此对于李雅普诺夫drift-plus-penalty方程有:

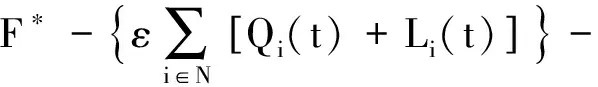
通过对不等式两边取期望并对t=0,1,2,…,T-1进行累加，可以得到:

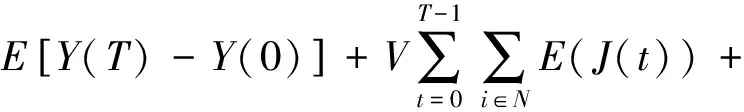
(15)

又因为Y(0)=0,Y(T)≥0,J(T)≥0，式(15)两边分别除以εT可以得到:

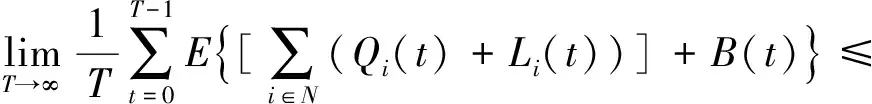
接下来证明平均能量的上限.对于式(15)，由于:

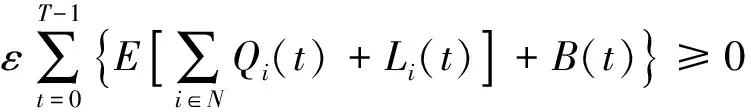
不等式两边同时除以TV，并令T→∞得到：

综上所述，系统的任务队列的堆积量和能量的上限得证.

证毕.

定理1表明，JOSA算法可以在V增加时近似实现离线最优化.同时，框架中的所有实队列和虚队列在时间平均意义下都是稳定的.

4 仿真评估

本文采用芬兰阿尔托大学和德国慕尼黑大学开发的机会网络模拟器ONE[31]，结合模拟器自带的虚拟城市区域场景对提出的JOSA算法进行了仿真评估.本文将宏基站设置在场景的中心，30台微基站随机分布在场景内，宏基站和微基站分别可同时关联50个和20个IoT设备.本文将微基站的功耗设置为190 W，由于宏基站需要一直开启，因此在仿真评估中不计算宏基站的能耗.对于IoT设备每个时间片的本地计算资源，本文考虑IoT设备CPU的工作频率为1.0 GHz.IoT设备的CPU和传输功率分别设置为60W和3W.IoT设备与基站之间的传输带宽为10 MHz，并采用文献[32]中的pass-loss和SINR模型.对于每个IoT设备在边缘服务器中的虚拟机资源，本文将每个设备的虚拟机CPU设置为单核1.5 GHz，所有用户共享20台16核物理CPU的服务器.IoT应用的平均到来量为1.5×106bps，任务处理密度为1 CPU cycles/b，延时为1个单位时间片长度.在仿真模拟执行过程中，IoT设备在场景内沿着道路按照WorkingDay移动模型移动.仿真模拟实验执行3 600个时间片.

4.1 仿真结果

Fig. 3 The impact of IoT devices number on the COMED system (V=1)图3 IoT设备的数量对系统的影响(V=1)

1) IoT设备数量对系统的影响.IoT设备的数量对系统整体的影响如图3所示.我们发现随着框架中IoT设备的增多，系统整体能耗与本地执行任务相比，有稳定在30%左右的整体节能率.随着IoT设备数量的逐渐增加，系统会开启更多的基站为设备提供服务.本地执行任务的比率相应上升，而卸载执行的任务比例下降.这是因为这组仿真中我们设置了只有1个时间片的严格的任务延时约束，即任务最多在系统中停留1个时间片.而当IoT设备增多时，服务器为每个用户提供服务的平均时间会减少，因此在严格的任务延时设置的条件下，IoT设备不得不选择本地处理未完成的任务，以满足应用的QoS要求.

2)V值对系统的影响.图4展示了不同的V值对于系统性能的影响.在李雅普诺夫优化理论中，V是权衡目标函数最优性和队列稳定性之间的参数.在COMED框架中，V用来权衡系统能耗与队列的稳定性.V值越大，代表系统更多关注于能量的节约，而更少关注队列的堆积状况.本文通过设置不同的V值，评估其对系统的能耗和队列堆积的影响.实验结果与理论相符，随着V的增大，系统的能量开销变少，更加节能.这是因为，当V较小时，系统会倾向于即时处理到来的任务，这种方式可能不是最节能的任务执行方式；而当V较大时，在延时允许的情况下，任务在系统中会不断堆积，等待最佳的执行任务的时机，例如IoT设备在本地积累一定的任务量，然后在某一个时间片将所积累的任务卸载到服务器上执行.

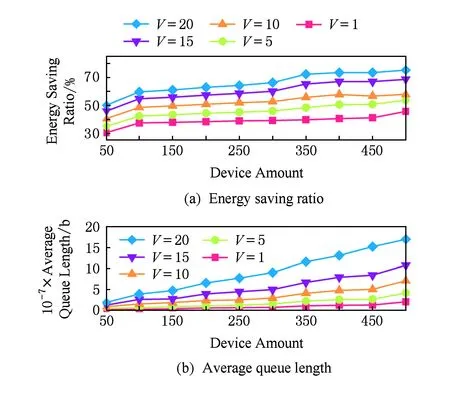
Fig. 4 The impact of V on the COMED system (dmax=5)图4 V对系统的影响(dmax=5)

3) 任务延时对系统的影响.不同的任务延时dmax设置对系统的影响结果如图5所示.dmax主要影响系统中队列堆积的上限.dmax设置的越长，系统中队列所能堆积的任务数量越多.与V对系统的影响类似，系统会为队列中堆积的任务寻找最佳的执行时机和方式，因此较长的任务延时设置将会节省更多的能量.

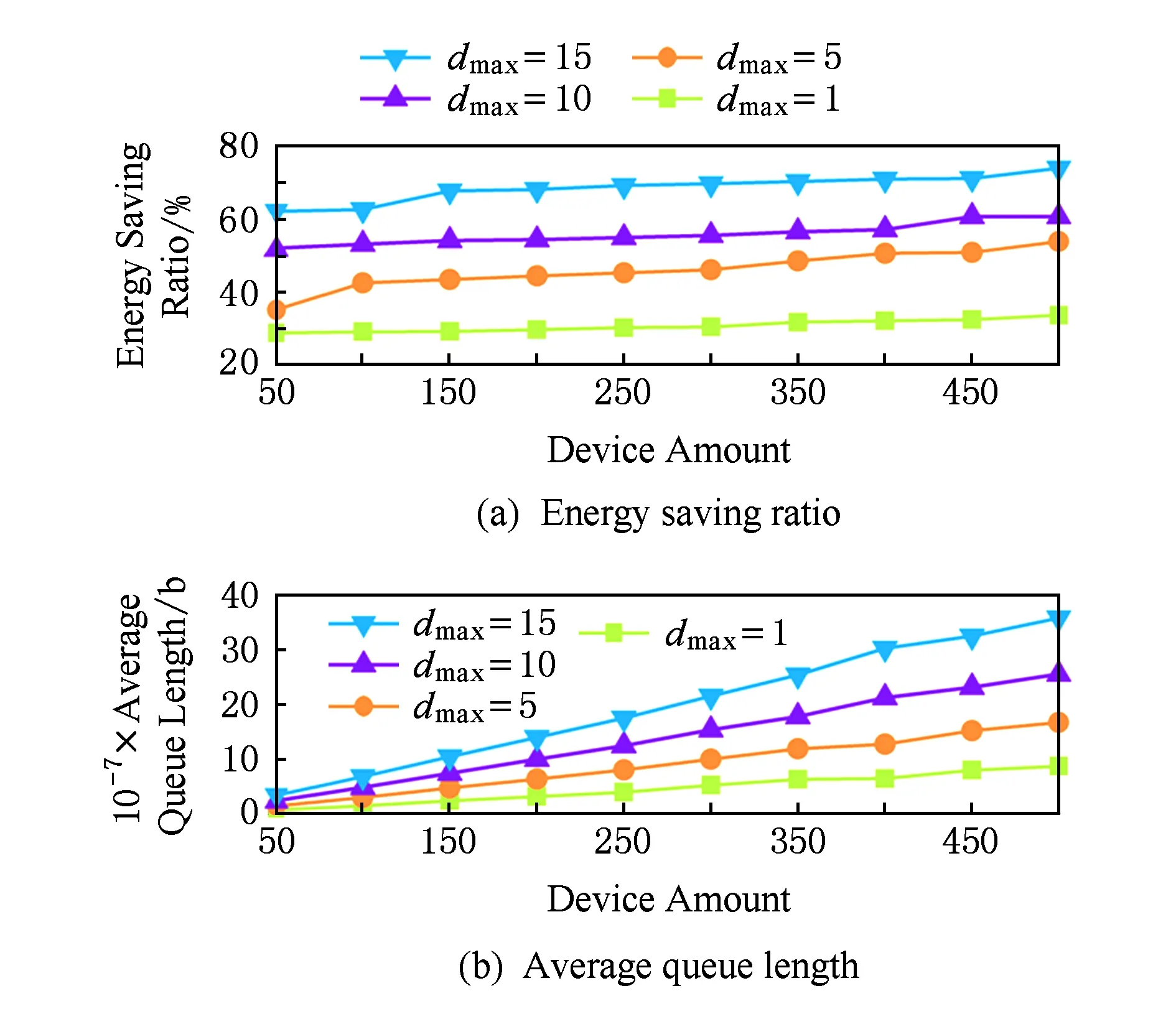
Fig. 5 The impact of the task delay on the COMED system (V=1)图5 任务延时设置对系统的影响(V=1)

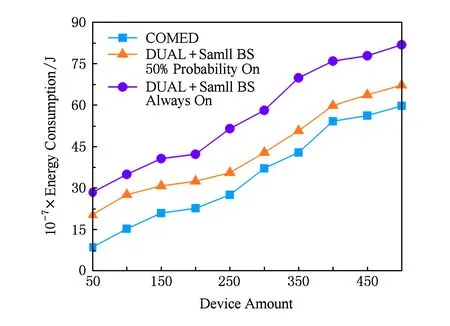
Fig. 6 System energy consumption versus DualControl algorithm图6 与DualControl算法的比较

4) 性能比较.由于目前很少有研究涉及任务卸载、基站睡眠与车辆-基站关联协同调度的研究，因此本文考虑使用目前已有的任务卸载策略与不同的基站调度策略相结合的方式与COMED框架进行比较.本文与2种方法进行了比较：①DualControl +微基站以50%的概率随机开启.DualControl[15]是一种用户-运营商协作任务调度策略，在假设云端服务器为每个移动设备分配一台虚拟机的前提下，通过用户调整CPU速度以及运营商将云资源分配给用户虚拟机最大化两者的整体效用；②DualControl+微基站一直开启.对于这2种策略，本文考虑其在调度过程中根据需求使用网络资源，但不考虑基站能耗对于调度策略的影响.图6展示了COMED框架与这2种方法的能量开销的比较结果.结果说明，任务卸载、设备-基站关联以及基站睡眠调度对框架的整体能耗起着至关重要的作用.换句话说，COMED框架将三者结合起来，对于系统整体的节能是有意义的.

5) 算法执行时间.本文在不同微基站数量的情况下，评估了IoT设备节点的数量对JOSA算法执行时间的影响.本文使用了一台处理器为Intel Core i5-2400 Processor@3.1 GHz的台式机对算法的执行时间进行了评估，结果如图7所示.JOSA算法有2个主要的步骤，步骤1用来调度IoT设备的任务执行和卸载量、设备基站-关联与基站睡眠，步骤2用来求解移动边缘服务器的任务调度.可以看到随着IoT设备的数量的增加，算法的2个步骤执行时间的增长都近似呈线性.在步骤1中，微基站数量和用户数量共同影响算法的执行时间.而在步骤2中，微基站的数量对算法的执行时间几乎没有影响.

Fig. 7 The execution time of the JOSA algorithm图7 JOSA算法执行时间

5 结束语

本文提出了一个基于超密集网络的移动边缘计算框架COMED.IoT设备通过与最适合的基站进行关联可以将任务卸载到移动边缘云服务器上执行，服务器根据定制的服务计划为每个IoT设备分配计算资源，在处理完设备卸载的任务后将结果传到互联网上.为了实现COMED框架，本文制定了一个任务卸载问题，通过对任务负载调度、设备-基站关联以及基站睡眠调度，旨在最小化IoT设备和基站的能耗，同时满足任务的延时限制.针对这一优化问题，本文提出了JOSA在线任务卸载算法，并通过理论分析和仿真实验证实了COMED框架的性能适用于IoT应用.

[1] Mach P, Becvar Z. Mobile edge computing: A survey on architecture and computation offloading[J]. IEEE Communi-cations Surveys & Tutorials, 2017, 19(3): 1628-1656

[2] Zhang Ke, Mao Yuming, Leng S, et al. Energy-efficient offloading for mobile edge computing in 5G heterogeneous networks[J]. IEEE Access, 2016, 4: 5896-5907

[3] Cisco. Cisco visual networking index: Global mobile data traffic forecast update, 2016—2021[OL]. [2017-09-23]. http://www.cisco.com/c/en/us/solutions/collateral/service-provider/visual-networking-index-vni/mobile-white-paper-c11-520862.html

[4] Wu Jun, Zhang Zhifeng, Hong Yu, et al. Cloud radio access network (C-RAN): A primer[J]. IEEE Network, 2015, 29(1): 35-41

[5] Ge Xiaohu, Tu Song, Mao Guoqiang, et al. 5G ultra-dense cellular networks[J]. IEEE Wireless Communications, 2016, 23(1): 72-79

[6] Wu Jingjin, Zhang Yujing, Zukerman M, et al. Energy-efficient base-stations sleep-mode techniques in green cellular networks: A survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 803-826

[7] Hu Yunchao, Patel M, Sabella D, et al. Mobile edge computing—A key technology towards 5G[OL]. [2017-09-23]. http://www.etsi.org/images/files/ETSIWhitePapers/etsi_wp11_mec_a_key_technology_towards_5g.pdf

[8] Brown G. Mobile edge computing use cases & deployment options[OL]. [2017-09-18]. https://www.juniper.net/assets/us/en/local/pdf/whitepapers/2000642-en.pdf

[9] Atreyam S. Mobile edge computing—A gateway to 5G era[OL]. [2017-09-18] http://carrier.huawei.com/～/media/CNBG/Downloads/track/mec-whitepaper.pdf

[10] Intel®Builders. Real-world impact of mobile edge computing (MEC)[OL]. [2017-09-18]. https://builders.intel.com/docs/networkbuilders/Real-world-impact-of-mobile-edge-computing-MEC.pdf

[11] Chen Xu. Decentralized computation offloading game for mobile cloud computing[J]. IEEE Trans on Parallel and Distributed Systems, 2015, 26(4): 974-983

[12] Chen Xu, Jiao Lie, Li Wenzhong, et al. Efficient multi-user computation offloading for mobile-edge cloud computing[J]. IEEE/ACM Trans on Networking, 2016, 24(5): 2795-2808

[13] You Changsheng, Huang Kaibin, et al. Energy-efficient resource allocation for mobile-edge computation offloading[J]. IEEE Trans on Wireless Communications, 2017, 16(3): 1397-1411

[14] Mao Yuyi, Zhang Jun, Letaief K B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3590-3605

[15] Kim Y, Kwak J, Chong S. Dual-side dynamic controls for cost minimization in mobile cloud computing systems[C] //Proc of the 13th IEEE Int Symp on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks. Piscataway, NJ: IEEE, 2015: 443-450

[16] Shojafar M, Cordeschi N, Baccarelli E. Energy-efficient adaptive resource management for real-time vehicular cloud services[OL]. [2017-09-01]. http://ieeexplore.ieee.org/document/7448886/

[17] Lyu X, Tian H, Sengul C, et al. Multiuser joint task offloading and resource optimization in proximate clouds[J]. IEEE Trans on Vehicular Technology, 2017, 66(4): 3435-3447

[18] Sardellitti S, Scutari G, Barbarossa S. Joint optimization of radio and computational resources for multicell mobile-edge computing[J]. IEEE Trans on Signal and Information Processing over Networks, 2015, 1(2): 89-103

[19] Cheng Jinkun, Shi Yuanming, Bai Bo, et al. Computation offloading in cloud-RAN based mobile cloud computing system[C] //Proc of the 17th IEEE Int Conf on Communications. Piscataway, NJ: IEEE, 2016

[20] Liu Dantong, Wang Lifeng, Chen Yue, et al. User association in 5G networks: A survey and an outlook[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1018-1044

[21] Kim J M, Kim Y G, Chung S W. Stabilizing CPU frequency and voltage for temperature-aware DVFS in mobile devices[J]. IEEE Trans on Computers, 2015, 64(1): 286-292

[22] Lin Yicheng, Bao Wei, Yu Wei, et al. Optimizing user association and spectrum allocation in HetNets: A utility perspective[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(6): 1025-1039

[23] Kwak J, Kim Y, Lee J, et al. DREAM: Dynamic resource and task allocation for energy minimization in mobile cloud systems[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(12): 2510-2523

[24] Han Siyang, Wang Xiao, Xu Linhai, et al. Frontal object perception for Intelligent Vehicles based on radar and camera fusion[C] //Proc of the 35th IEEE Chinese Control Conf. Piscataway, NJ: IEEE, 2016: 4003-4008

[25] Yan Ming, Chan C A, Li Wenwen, et al. Network energy consumption assessment of conventional mobile services and over-the-top instant messaging applications[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3168-3180

[26] Little J D C, Graves S C. Little’s law[G] //Building Intuition. Berlin: Springer, 2008: 81-100

[27] Neely M J. Stochastic network optimization with application to communication and queueing systems[J]. Synthesis Lectures on Communication Networks, 2010, 3(1): 1-211

[28] Fisher M L. The Lagrangian relaxation method for solving integer programming problems[J]. Management Science, 1981, 27(1): 1861-1871

[29] Schrijver A. Theory of Linear and Integer Programming[M]. New York: John Wiley & Sons, 1998

[30] Berenstein C A, Gay R. Complex Variables: An Introduction[M]. Berlin: Springer Science & Business Media, 2012

[31] Keränen A, Ott J, Kärkkäinen T. The ONE simulator for DTN protocol evaluation[C] //Proc of the 2nd Int Conf on Simulation Tools and Techniques. New York: ACM, 2009: Article No.55

[32] Bethanabhotla D, Bursalioglu O Y, Papadopoulos H C, et al. User association and load balancing for cellular massive MIMO[C] //Proc of the 5th Information Theory and Applications Workshop. Piscataway, NJ: IEEE, 2014: 1-10