带碰撞角约束的三维有限时间滑模制导律
赵曜,李璞,刘娟,陈喆,刘向东
(1.中国运载火箭技术研究院,北京 100076; 2.国防科学技术大学,长沙 410073;3.北京理工大学 自动化学院,北京 100081)
末制导的首要任务是控制导弹精确命中目标,随着科技的日新月异,现代军事应用对末制导技术的性能要求也日益提高。在某些特定的情况下,为了增强打击的毁伤效果或发挥导弹所携弹头的最大杀伤能力,往往需要导弹从指定的方向、以特定的姿态对目标进行打击,因而产生了带碰撞角度约束的制导问题[1]。
由于形式简单、所需的信息量少,比例制导在实际工程领域得到了广泛的应用[2-4]。然而传统的比例制导方法只能够实现末端脱靶量为零,对于碰撞角约束要求无法满足。为了解决上述问题,学者们提出了多种改进的比例制导方法[5-9]。一种较为典型的方法是偏置的比例制导。这类方法是在传统的比例制导律的基础上添加一个时变偏置项以消除碰撞角误差[5-6]。然而,偏置的比例制导在对目标进行追尾打击时性能会急剧下降[9]。另一种改进的比例制导方法是通过在线更新比例系数得到的。文献[7]针对高超声速滑翔飞行器打击地面静止目标提出了一种自适应三维末制导律,该制导律的比例系数以特定的闭环形式进行连续更新,使得导弹的弹道倾角和偏角末值均满足期望要求。然而在初始指向误差较大的情况下,文献[7]的方法会给制导初段带来巨大的诱导阻力并导致较长的飞行时间。为了解决该问题,Ratnoo和 Ghose[8]在制导初始段设计了一种定向制导,该制导律也是比例系数随时间变化的比例制导。文献[9]进一步对该方法进行了扩展,使其能够打击常值速度目标。然而文献[8-9]中提出的制导方法仅能应用于二维平面。
作为一种变结构控制方法,滑模控制对模型不确定性和外部扰动有着较强的鲁棒性,因而在末制导系统设计中得到了广泛的应用。周荻等[10]针对寻的导弹提出了一种自适应滑模制导律,并分别通过理论分析和数值仿真验证了制导律对参数摄动的鲁棒性。然而,该制导律并未考虑碰撞角约束。Shima[11]基于滑模控制提出了一种拦截角度约束制导律,该制导律能够应用于对目标进行迎头打击、尾追打击和弹头追踪打击等情形。文献[12]进一步考虑了时变的加速度边界约束,对 Shima[11]的制导律进行了扩展研究。但是该制导方法并未考虑导弹的气动特性。Hou和Duan[13]基于自适应滑模控制方法设计了整合的制导控制策略,并通过非线性导弹模型对制导律的有效性进行了验证。但是该制导律仅研究了弹目在同一二维平面的情形,并且可实现的碰撞角范围非常有限。因此,需要进一步研究可实现碰撞角范围较广且能应用于三维空间的滑模制导方法。
彭双春等[14]结合微分几何和李群方法的优点,设计了一种三维制导律,但是该方法精度对制导参数的优化结果较为敏感。文献[15]利用变结构控制方法设计了鲁棒制导律,然而该方法设计时忽略了导弹的动态特性。基于非线性最优控制理论,文献[16]提出了一种模型预测静态规划三维制导律,该制导方法不仅能够满足期望的终端约束,也能使制导指令最小化。然而,应用该方法需要首先提供指令初解,然后通过在线优化得到实际制导指令,且优化的收敛速度与初解精度直接相关。文献[17]基于状态相关黎卡提方程方法设计了带碰撞角约束的三维制导律,该方法虽然不需要提供初解信息,但是仍需在线求解状态相关黎卡提方程,计算量较大,不利于弹上计算机求解。
本文基于导弹的非线性运动学和动力学模型提出了一种三维有限时间滑模制导方法,实现了以期望的碰撞角对地面静止目标的打击要求。首先根据终端约束条件设计了滑模函数,然后利用Lyapunov方法得到了解析的制导律并证明了闭环系统的稳定性。本文提出的制导方法具有以下优势:①无需对模型作解耦或线性化处理;②纵向和侧向平面碰撞角约束均能满足且可实现的碰撞角范围较大;③得到了解析的制导指令,在线计算量小;④闭环系统对外界扰动和参数不确定性不敏感。
1 系统模型
导弹三维质点运动学模型[17]为

式中:(x,y,z)为导弹质心位置坐标;V、γ和 χ分别为导弹的速度、弹道倾角和弹道偏角;D为阻力;g为重力加速度;m为导弹质量;ay和az分别为导弹法向和侧向加速度,与导弹速度矢量垂直,因而只改变导弹的速度方向,不改变速度大小。令(xf,yf,zf)为目标的位置坐标,γf和 χf分别为纵向和侧向期望的碰撞角末值。带碰撞角约束的三维末制导问题可描述为:设计制导律,使得脱靶量和碰撞角误差在导弹落地时刻同时收敛为0,即设计ay,az,使得下式成立:

2 制导律设计
首先,构造2个新变量 λ1和 ξ1,具体形式如下所示:

式中:Y=y0-y,y0为导弹初始高度值;因为Y仅与高度信息相关,因此称其为“伪高度变量”;Yf为Y的末值。
以Y为自变量对式(3)求微分,可得
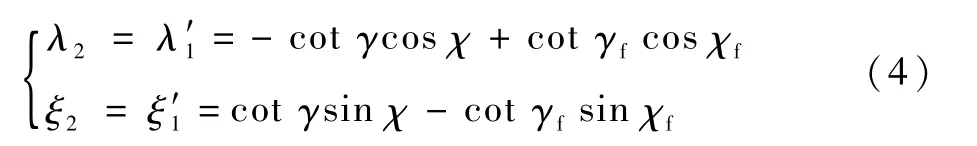
由式(3)和式(4)容易得到以下结论:如果λ1、ξ1、λ2和 ξ24个变量在Y→Yf时(即y→yf时)同时收敛为 0,则有x=xf,z=zf,γ=γf,χ=χf,期望的设计指标(见式(2))也就得到了满足。
基于上述结论进行带碰撞角约束的有限时间滑模制导律设计,首先给出以下定理:
定理1考虑一变量 σ1,将其对Y求导得到σ2。如果将σ2作为控制量,且其具有如下形式:

则σ1和σ2将会在Y=Yf时同时收敛为0。
证明由式(5),可得到如下等式关系:
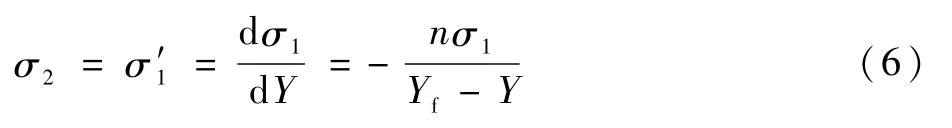
通过调整变量位置,可将式(6)整理成如下形式:
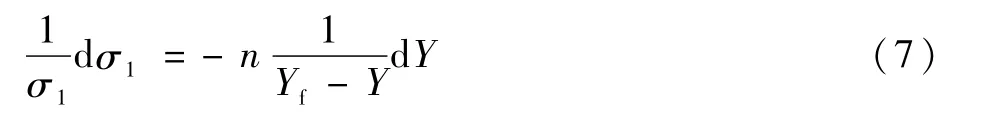
假设式(7)的初始状态为(Yb,σ1b)。则将式(7)从(Yb,σ1b)积分到未来某状态点(Y,σ1)可得

由式(8)可推得
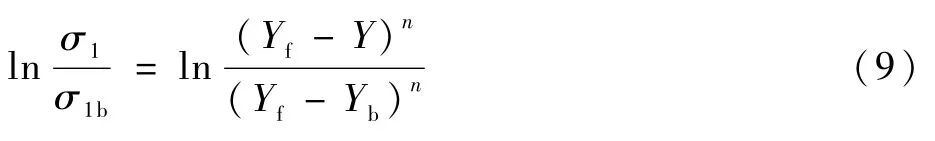
将式(9)两边取指数运算,即可得到 σ1的解析表达式如下:

再将式(10)对Y求微分,可进一步得到 σ2的解析表达式:

由式(10)和式(11)可以看出,如果n>1成立,则在Y=Yf时σ1和σ2将会同时收敛到0。
通过以上定理可以发现,式(5)给出了 σ2的一条合理的变化轨迹,即如果σ2按照式(5)定义的轨迹变化,则σ1和σ2将会在Y=Yf时同时收敛为0。因此,制导律的设计目标可以转化为通过设计控制器使得λ2和 ξ2均按照式(5)定义的轨迹变化来实现。
设计有限时间滑模控制器来实现上述指标要求。首先对 λ2和 ξ2再求一次微分,可以得到如下等式:

令式(12)中的 γ′,χ′为辅助控制量,实际控制量ay,az可由辅助控制量求得。利用式(3)和式(4)中的变量 λ1,ξ1,λ2,ξ2,设计如下的滑模函数:

令式(14)和式(15)均等于 0,联立求解可得到如下等效控制:

选取如下形式的控制量:

式中:等效控制量 γ′eq和 χ′eq由式(16)给出;γ′dis和χ′dis为切换控制量。
将式(19)代入式(18),经整理可得

根据 Lyapunov稳定性理论,若V′1≤0且V′2≤0,则闭环系统稳定。因此,可令
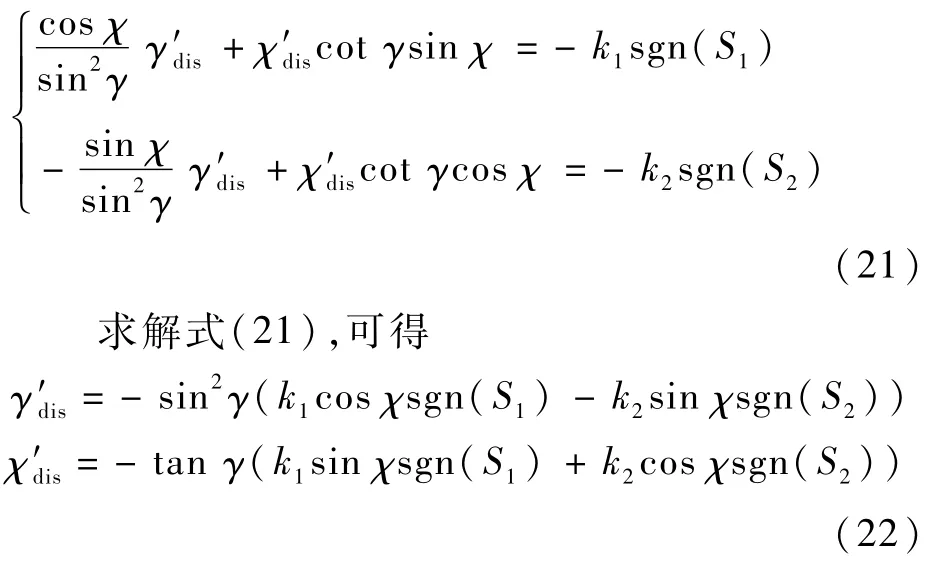
式中:k1、k2为切换增益。将式(16)和式(22)代入式(19)即可得到辅助控制量为

进一步将式(23)结果代入式(14)和式(15),可得

从式(24)可以看出,参数k1和k2的物理意义分别为滑模函数S1和S2接近滑模面的速率。因此,可将切换增益设计如下:

其中:Yb=pYf,p∈(0,1),因此有Yb<Yf。滑模函数S1和S2将在Y=Yb时收敛到零,即Y∈[Yb,Yf]时,有S1=S2=0。由上述结论可知,设计的控制律式(23)可使得 λ2和 ξ2在Y∈[Yb,Yf]时均按照式(5)定义的轨迹变化。进而由定理 1可知 λ1、ξ1、λ2和 ξ24个变量在Y=Yf时同时收敛为 0,将式(3)和式(4)代入求解,易得即满足了期望的设计指标式(2)。因此,可得到结论:在控制律式(23)作用下,导弹能以期望的弹道倾角和弹道偏角对目标进行精确打击。
结合式(1)和式(23),可得到如下带碰撞角约束的三维制导律:

在制导律式(26)作用下,系统状态在达到滑模面之后会沿着滑模面继续滑动,此时控制律中的切换函数会引起抖振现象。为了抑制抖振,采用了饱和函数法,即用连续的饱和函数sat(S)去近似切换函数sgn(S)。饱和函数选择为如下形式:

式中:ε为边界层厚度,其值需要折中选择。边界层厚度越大,对抖振的抑制效果也越好,但是相应的静态误差也会越大;边界层厚度越小,对抖振抑制效果越弱,但是相应的静态误差也会越小。
3 数值仿真
本节通过数值仿真验证本文所提制导律的有效性,导弹气动数据取自文献[18]。导弹在三维空间中的初始位置坐标为(x0,y0,z0)=(0,3,3)km,初始速度为V0=600m/s,目标位置坐标为(xf,yf,zf)=(10,0,1)km。制导参数选择为n=3,p=0.3,ε=0.001。需要指出本节所有的仿真算例均考虑了一阶自动驾驶仪滞后特性,滞后时间选为0.3 s。仿真结束条件设定为y=0m,即导弹落地时刻。
首先选择了不同的初始发射角进行仿真。其中,发射角(γ0,χ0)分别选为(-5°,0°),(-15°,30°)和(-30°,-30°),碰撞角(γf,χf)选择为(-60°,30°)。仿真结果如图 1所示。
从以上结果可以看出,虽然导弹的初始发射方向不同,但最终均能以期望的碰撞角对目标实现精确打击。对于(γ0,χ0)为(-15°,30°)和(-30°,-30°)的算例,由于初始指向误差较大,因此在初始时刻通过较大的法向和侧向过载对导弹的指向进行了修正。当导弹的弹道倾角和弹道偏角进入合理的范围内时,过载幅值也下降到较小的范围。此外,通过滑模函数变化曲线可以发现,虽然到达滑模面的时间不同,但是只要在碰撞时刻之前到达滑模面,期望的终端约束就能得到满足。
然后通过蒙特卡罗仿真验证有限时间滑模制导律对外界扰动和参数不确定性的鲁棒性。导弹的初始发射角(γ0,χ0)和期望的碰撞角(γf,χf)分别选择为(-5°,10°)和(-70°,60°)。仿真中,在制导指令输入端加入范围为±20%指令幅值的随机干扰作为外部扰动。此外,参数不确定性通过施加范围为大气密度标称值±5%的随机噪声来实现。进行1 000次的蒙特卡罗仿真,得到结果如图2所示。

图1 不同发射角条件下仿真结果Fig.1 Simulation results with different launch angles
由于仿真结束条件设定为y=0,因此,脱靶量可由x坐标和z坐标的末值分布来体现。图2(a)给出了脱靶量的蒙特卡罗仿真结果,可以看出1 000次蒙特卡罗仿真碰撞点的x坐标和z坐标范围分别在(9 999.94,10 000.06)m和(999.997,1000.003)m之间,说明脱靶量非常小。碰撞角的蒙特卡罗仿真结果可参见图2(b)。从该结果可以看出,弹道倾角和弹道偏角的末值范围分别在(-70.2°,-69.8°)和(59.2°,60.9°)之间,因此,碰撞角误差也非常小。该组仿真结果验证了本文所提制导方法能够保证较高的终端精度。
为了进一步验证本方法的鲁棒性优势,图3中给出了应用文献[17]制导律得到的蒙特卡罗仿真结果。对比图2和图3可以发现,相较于文献[17]的方法,本文方法对外部扰动和模型不确定性具有更强的鲁棒性。
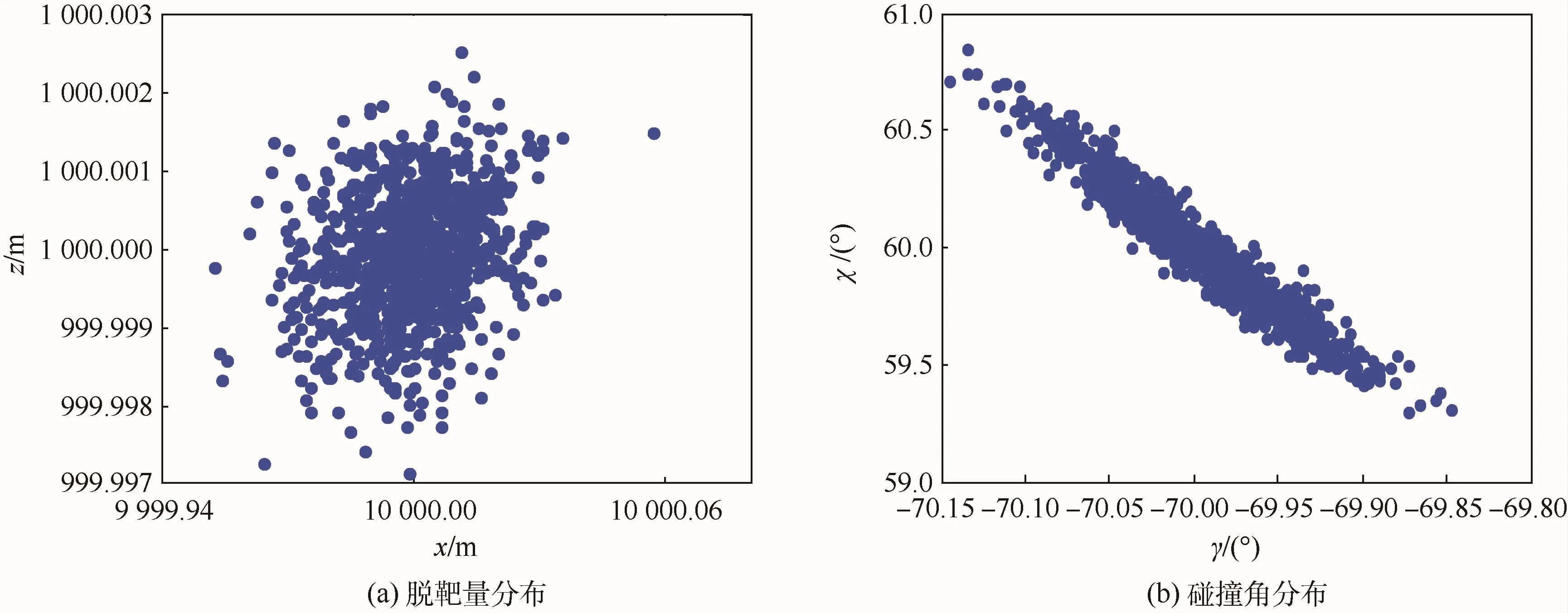
图2 本文制导律蒙特卡罗仿真结果Fig.2 Results of Monte Carlo simulation with proposed guidance law
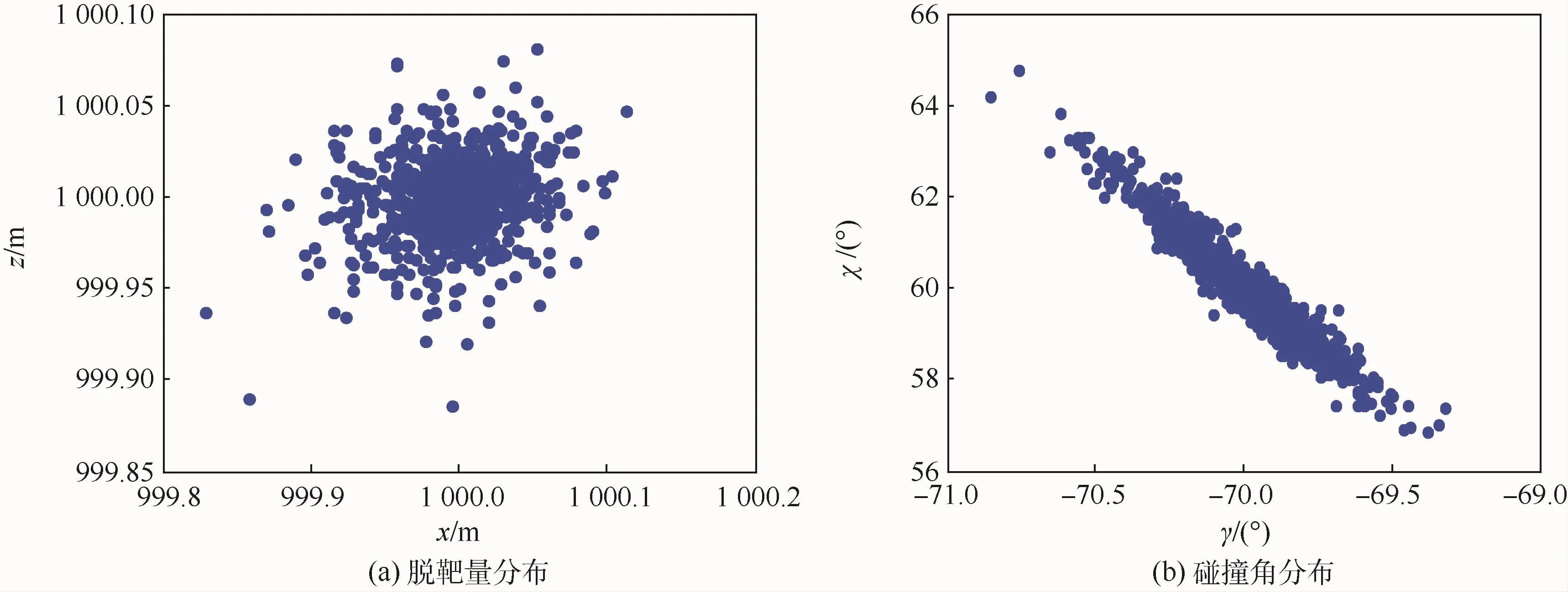
图3 文献[17]制导律蒙特卡罗仿真结果Fig.3 Results of Monte Carlo simulation with guidance law in Ref.[17]
4 结 论
本文提出了一种三维有限时间滑模制导律,不仅实现了导弹对地面静止目标的精确打击,也实现了对纵向和侧向碰撞角的约束。该制导方法无需对系统模型进行解耦或线性化处理,制导律形式简单且需求信息量较少。数值仿真结果验证了该制导律能保证很高的终端精度,且对初始指向误差、外界扰动及参数不确定性具有较强的鲁棒性。在今后研究中,还需将该制导方法扩展到打击机动目标的情形。
(References)
[1]KIM M,GRIDER K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859.
[2]SIOURISG M.Missile guidance and control systems[M].Berlin:Springer,2003.
[3]ZARCHAN P.Tactical and strategic missile guidance[M].4 th ed.Rest on:AIAA,2002.
[4]GHAW S N,GHOSE D.Pure proportional navigation against time-varying target maneuvers[J].IEEE Transactions on Aerospace and Electronic Systems,1996,32(3):1336-1346.
[5]KIM B S,LEE JG,HAN H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
[6]JEONG S K,CHO S J,KIM E G.Angle constraint biased PNG[C]∥Proceedings of 5 th Asian Control Conference.Piscataway,NJ:IEEE Press,2004:1849-1854.
[7]LU P,DOMAN D B,SCHIERMAN JD.Adaptive terminal guidance for hypervelocity impact in specified direction[J].Journal of Guidance,Control,and Dynamics,2006,29(2):269-278.
[8]RATNOO A,GHOSE D.Impact angle constrained interception of stationary targets[J].Journal of Guidance,Control,and Dynamics,2008,31(6):1816-1821.
[9] RATNOO A,GHOSE D.Impact angle constrained guidance against non stationary non maneuvering targets[J].Journal of Guidance,Control,and Dynamics,2010,33(1):269-275.
[10]ZHOU D,MU C D,XUW L.Adaptive sliding-mode guidance of a homing missile[J].Journal of Guidance,Control,and Dynamics,1999,22(4):589-594.
[11] SHIMA T.Intercept-angle guidance[J].Journal of Guidance,Control,and Dynamics,2011,34(2):484-492.
[12]TAUB I,SHIMA T.Intercept angle missile guidance under time varying acceleration bounds[J].Journal of Guidance,Control,and Dynamics,2013,36(3):686-699.
[13]HOU M Z,DUAN G R.Integrated guidance and control of homing missiles against ground fixed targets[J].Chinese Journal of Aeronautics,2008,21(2):162-168.
[14]彭双春,潘亮,韩大鹏,等.一种新型三维制导律设计的非线性方法[J].航空学报,2010,31(10):2018-2025.PENG S C,PAN L,HAN D P,et al.A new 3D guidance law based on nonlinear method[J].Acta Aeronautica et Astronautica Sinca,2010,31(10):2018-2025(in Chinese).
[15]佘文学,周凤岐.三维非线性变结构寻的制导律[J].宇航学报,2004,25(6):681-685.SHE W X,ZHOU F Q.High precision 3-D nonlinear variable structure guidance law for homingmissile[J].Journal of Astronautics,2004,25(6):681-685(in Chinese).
[16]OZA H B,PADHIR.Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles[J].Journal of Guidance,Control,and Dynamics,2012,35(1):153-164.
[17]RATNOO A,GHOSE D.State-dependent Riccati-equationbased guidance law for impact-angle-constrained trajectories[J].Journal of Guidance,Control,and Dynamics,2009,32(1):320-325.
[18]IMADO F,KURODA T,TAHK M J.A new missile guidance algorithm against a maneuvering target[C]∥Proceedings of the AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,1998:145-153.

