南方典型毛竹经营区土壤养分空间变异特征1)——以福建省南平市顺昌县毛竹林经营区为例

赖壮杰 刘健 余坤勇 俞欣妍 陈樟昊

(福建农林大学，福州，350002)

土壤是植物生长繁育的基质，土壤养分是土壤重要属性之一[1]。在不同成土因素的综合影响下土壤理化性质存在明显的空间异质性[2]。土壤随空间位置发生变异的规律是土地管理和现代农业经营的重要依据。土壤养分空间异质性是土壤属性空间异质性的重要方面，直接调控植被的分布和植物群落的组成[3-4]。因此，研究土壤养分空间异质性对分析土壤养分与植物空间分布的关系具有重要意义_bookmark5。

国内外许多学者对于土壤特性空间变异性规律的研究最早可追溯到20世纪50年代[5]。近年来，土壤空间异质性成为土壤科学研究的重要内容，对土壤属性空间异质性研究开始由定性描述转向定量。Webster et al.[6]将地统计学理论成功与土壤的空间分布相结合,推动了土壤领域的研究进展。早期主要应用于土壤中氮、磷、钾等土壤养分的相关性研究，近年来国内许多学者从多角度、多尺度对土壤养分空间变异进行了大量研究[7-10]。由于土壤养分分布的空间异质性受不同地形、不同母质、多种植被类型等结构性因素和采样、测量误差等随机因素的影响，且土壤受人为强烈干扰，不同地域的土壤性质存在着差异性[11]。

竹类资源是我国森林资源重要的组成部分[12]。毛竹(Phyllostachysheterocyclacv．Pubescens)是我国面积最大，分布最广的笋材两用竹种，在我国林业生产中占有重要的地位[13-14]。当前，毛竹科学经营水平普遍较低，毛竹的生产效率和质量不高的状况仍很普遍，提高毛竹的产量与经营水平就成为了当务之急[15]。顺昌县是我国的毛竹之乡，现有竹林面积30 000 hm2，占有林地面积21.2%，农村户均竹林0.91 hm2，人均0.18 hm2，毛竹为该县的优势资源[16-17]。随着市场经济的发展，竹农经营竹林使用大量的化学肥料，造成不合理的施肥和浪费，导致竹林生态系统失衡，甚至退化[18-20]。为了科学经营竹林，合理利用土地，明确土壤养分在空间上的变异及分布[21]。以顺昌县典型毛竹经营区为对象，运用地统计学与GIS的空间分布技术等相关方法，分析研究区域毛竹林土壤养分空间异质性，以期为竹林的有效经营提供科学依据。

1 研究区概况

研究区位于福建省南平市顺昌县西北部(117°30′～118°14′E，26°39′～29°12′N)，属亚热带季风气候，年平均降水量1 752 mm，年平均日照时间1 700 h，年平均气温为16.3 ℃，极端温度最高为37 ℃，最低为-4 ℃。研究区森林资源丰富，森林覆盖率为75.6%，林业用地占土地总面积的78.8%，主要优势树种有杉木(Cunninghamialanceolata)、毛竹等，土壤类型为红壤和黄壤。

2 研究方法

2.1 土壤样本的采集与处理

在顺昌县大干镇开展数据采集工作，根据毛竹林的分布，采用分散布点与定点集中测量相结合的方法，选取59个点为采样点，每个样地用2台GPS进行定位，要求显示的坐标误差小于10 m。样地毛竹长势良好、叶量充足、叶片健康，每个采样点分三层取土，即：0～20、>20～40、>40～60 cm土壤层，每层取1个环刀进行理化性质的测定。

将土样带回实验室进行风干、研磨以及过筛(2.00、1.00、0.25 mm)。土壤全氮数据采用VARIO MAX碳氮元素分析仪进行测定。水解氮采用扩散法、速效钾采用乙酸铵火焰光度计法、有效磷采用双酸浸提法、有机质采用重铬酸钾容量法[22]。

2.2 数据分析

地统计学分析：本文主要运用地统计学的半方差函数理论。半方差分析是运用半方差函数，对采样数据进行空间相关分析，理论模型主要包括高斯指数和球面模型，包括通常选择使用测量数据估计实验变异函数。半方差变异函数(λ(h))的每个样点计算使用方程如下：

式中:h表示步长，也称为样本距；λ(h)表示样本距为h的土壤变量半方差变异函数；Z(xi)和Z(xi+h)分别表示变量Z在空间位置xi与xi+h上的取值；N(h)表示样本距离为h时的样点对数。

在这项研究中，高斯模型(G)、指数模型(E)和球面模型(S)被用来探索土壤分布的空间连续性和各种土壤元素含量的分布结结构，其最佳模式是根据最大的决定系数(R2)和最小的残差平方和(RSS)[23-24]。土壤性质的空间变异采用地统计学的半方差函数拟合，块金值、基台值、块基比、有效变程的参数对拟合范围内的未知点进行估值。

克里格插值:克里格法是在结构分析和变异函数的理论基础上，对空间局部进行插值或进行无偏估计的方法，可根据拟合的模型结构和已知空间坐标的原始数据对区域范围内的未知点进行最优无偏估值。本文主要采用普通克里格方法，克里格插值是以地统计学为基础，以观测值对位置点进行估算，将得到的变量放入空间分布中表现出来。其本质是进行局部估计的加权平均值，即已知的数据点估测未知的分布于图上的点，表达式如下：

式中:Z(x0)为位置点x0的估算值，Z(xi)为x0点附近的若干观测值，λi为第i个样本点的权重，n为样本的个数。

全局趋势分析：全局趋势分析主要是反映物体在空间区域的总体变化趋势，从宏观层面揭示研究区的总体规律，并忽略局部的变异。本研究的林地土壤化学指标空间分布趋势，将通过全局趋势分析进行说明。趋势分析主要是运用GIS软件的趋势面分析功能，将研究区内抽样得到的样点属性值作为依据，拟合一个数学曲面，用该曲面反映研究区抽样点属性值，以及整体研究区某一属性值的空间分布情况。为了使模拟的短程随机变异更精确，使全局趋势对局部半方差变异分析过程中产生的影响减少，各土壤养分趋势分析可采用趋势面分析。

3 结果与分析

3.1 毛竹林地土壤养分统计分析

从表1可知，土壤pH值的变动范围是4.09～5.57，速效钾、有效磷、水解氮等速效养分质量分数的变动范围分别为28.35～186.38、0.71～4.90、21.81～276.77 mg/kg；有机质、全氮质量分数的变动范围分别是4.37～105.19 g/kg、0.05%～0.48%。变异系数的大小能够反映土壤特性空间变异性强弱，一般变异系数小于10%时被认为变异性弱，变异系数在10%～100%范围内被认为是中等变异，当变异系数大于100%时，被认为具有强烈的变异性[25]。变异程度按照强到弱的排序为：水解氮、速效钾、全氮、有效磷、有机质，其中速效钾(42.48%)、有效磷(36.61%)、水解氮(53.56%)、有机质(54.35%)、全氮(42.28%)均属于中等变异，pH值(6.49%)属于变异性弱，说明研究区土壤pH值相对稳定。

表1 毛竹林林地土壤养分指标数据统计特征值

3.2 半方差函数拟合

由表2可知，土壤全氮、有效磷、水解氮的决定系数分别为0.950、0.921、0.888，均大于0.8，表明具有很好的半方差结构，说明理论模型能够较好的反映其空间分布特征；有机质的决定系数为0.620，有较好的半方差结构，拟合程度中等；速效钾与pH值的决定系数较小，分别为0.412、0.433，拟合程度相对较差，表明速效钾与pH的空间自相关性不太明显。

由表2可知，pH值的有效变程为1 220 m，水解氮的有效变程为920 m，全氮、有机质、速效钾的有效变程较小，分别为640、390、430 m，表明全氮、有机质、速效钾等指标的自相关距离较小，而有效磷指标的有效变程达到了8 720 m，表明其指标具有很大的自相关距离，空间连续性很强。

各养分与pH值的基台值均为正值，是由实验误差与采样失误导致的基底效应所致。块基比为基底效应，表示样本间的变异特征，随机因素会引起块基比值的变化，比值越大表明样本之间的变异越多。通过块基比的大小可以看出，随机因素由多至少的排序为：有效磷、全氮、速效钾、水解氮、pH、有机质。因此，说明土壤有效磷的分布包含更多的随机因素，有机质的分布则随机因素最少。同时，空间相关性的强弱也可以由块基比反映，块基比的数值越小，代表空间相关性越强。一般认为块基比值小于25%，变量具有强烈的空间相关性；块基比值在25%～75%，变量具有中等空间相关性；块基比值大于75%，变量的空间相关性较弱[26]。由此可知，有机质、全氮、pH、水解氮、速效钾的块基比值均小于25%，表明各因素具有强烈的空间相关关系，有效磷的块基比数值为30.42%，介于25%～75%，其空间分布为中等相关关系。

表2 土壤速效养分空间变异的理论模型与相应参数

注：E表示指数模型，S表示球状模型，G表示高斯模型。

3.3 土壤养分的空间分布趋势

由图1可知，土壤速效钾养分在东至西方向较为平滑，自西向东略有下降趋势，研究区采样数据在南北方向具有明显的“倒U型”趋势，中部方向速效钾质量分数高于研究区南北方向；土壤有效磷养分在西南至东北方向具有明显的“U型”趋势，中部有效磷质量分数低于西南、东北方位，有效磷自西北至东南方向，质量分数总体呈现上升趋势，西南至中部有效磷质量分数上升趋势明显，研究区中部至东南方向趋于稳定，略有下降；水解氮自西向东总体趋势为上升趋势，研究区西部至中部上升趋势明显，中部至东部总体趋势稳定，略有下降，南北方向水解氮分布具有明显的“U型”趋势，中部水解氮质量分数明显低于研究区北部与南部；有机质在东西方向的分布与水解氮相似，都是自西向东总体趋势为上升趋势，研究区西部至中部上升趋势明显，中部至东部总体趋势稳定，略有下降，而南北方向则与水解氮相反，呈“倒U型”，中部有机质质量分数明显高于研究区北部与南部；全氮在东西方向的分布与有机质变化规律相似，自西向东总体呈现上升趋势，自西向东呈现缓慢上升趋势。pH在研究区西部至东部较为平稳，西部至研究区中部有略微下降，中部至研究区东部具有微弱的上升趋势，pH在南北方向具有明显的“U型”趋势，中部土壤偏酸性，北部与南部的土壤酸碱度较为适宜。

每根竖线代表一个样点的属性值，平面坐标表示样点的投影；Z轴表示土壤养分质量分数及pH的数值；速效钾、水解氮、有机质、全氮以及pH的X轴正向表示正东方向，Y轴正向表示正北方向；有效磷X轴正向表示东北方向，Y轴正向表示西北方向。

图1研究区内各土壤养分指标的自然分布状况

3.4 毛竹林地土壤养分空间插值分析

由表3可知，标准平均值均较小，趋近于0；均方根预测误差与平均标准误差较为接近，只有水解氮例外；标准均方根预测误差趋近于1，即各养分与pH的指标插值精度较高，可以用于土壤养分空间分布的预测。

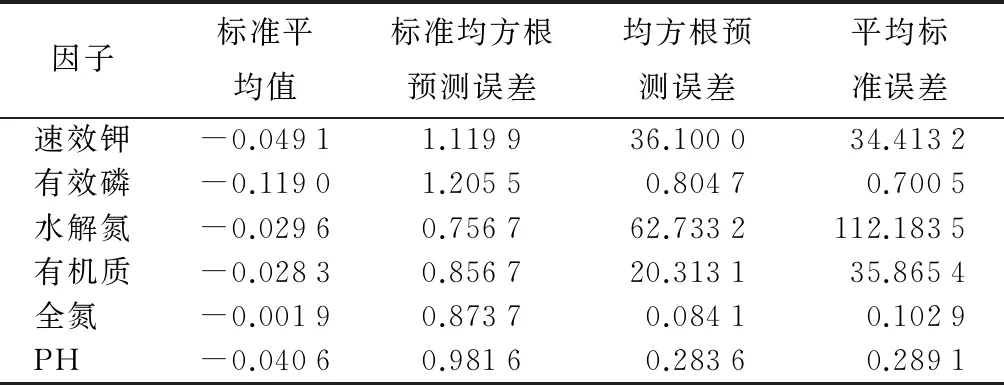
表3 插值精度验证参数

由图2可知，速效钾质量分数在研究区内分布较为平均，西部高于东部，中部高于两侧；水解氮东部颜色深于西部，中部颜色深于四周，表明研究区中部土壤水解氮质量分数优于四周，且研究区东部土壤水解氮质量分数大于西部；有效磷在研究区内东北部极其缺乏，南部土壤有效磷质量分数多于其他地方，其次是西部有效磷质量分数高于北部；有机质含量在研究区内分布较集中，且质量分数较高，研究区中部的有机质质量分数高于四周，中部偏东地区有机质丰富；土壤中全氮的质量分数东部高于西部，南部高于北部，中部偏南地区土壤全氮质量分数最高；pH值四周颜色较深，中部颜色最浅，北部颜色深于南部，表示研究区中部土壤酸性强与四周，北部土壤酸碱度较适宜毛竹林的种植。可见，克里格插值得到的土壤养分分布图结果与土壤养分空间趋势图基本吻合。

图2 毛竹林土壤养分含量空间分布

4 结论与讨论

在研究区域内，除pH值属于弱变异性外，速效钾、有效磷、水解氮、有机质、全氮均属于中等变异，说明研究区土壤pH值相对稳定。对于采样点的设置，土壤养分的自相关距离具有指导意义，可采用地统计学对在自相关距离以内的采样点进行分析[27]，因为土壤养分的空间自相关范围的测度受其变程的影响，所以在土壤养分取样设计时，其变程具有一定的指导作用[28]。通过研究分析，6种土壤养分的空间相关范围较大(390～8 720 m)，速效钾的变程最小(430 m)，有效磷指标的有效变程最大，有效变程达到了8 720 m。全氮、有机质、速效钾有效变程较小(430～640 m)，说明影响土壤全氮、有机质、速效钾的生态过程基本在相同的尺度上起作用。

通过克里格插值图交叉检验可见，水解氮、有机质、pH值及全氮的含量东边高于西边，速效钾则是西边高于东边，而速效钾中部高于两边，西边也相对高于东边。从研究区总体看，土壤的pH值为(4.82±0.31)，土壤呈酸性，pH值的变异系数为6.49%属于弱变异性，pH在研究区西部至东部较为平稳，西部至研究区中部有略微下降，中部至研究区东部具有微弱的上升趋势，pH在南北方向具有明显的“U型”趋势，中部土壤偏酸性，北部与南部的土壤酸碱度较为适宜。土壤中速效钾、水解氮、全氮与有机质的含量充分，可以满足毛竹生长对养分的需求，但有效磷质量分数仅为(2.37±0.87)mg/kg，质量分数低于正常范围，这是由于调查区位于中国南部，大部分土壤为黄壤与红壤，土壤中普遍缺少磷元素，此调查结果与林振清[29]在建瓯市的调查结果相近，与郭晓敏[30]研究的结果相似。但在毛竹生长过程中，虽然对磷元素的需求量没有氮元素高，但磷元素的缺乏也将严重影响毛竹林分的生长[31]。研究区中部土壤水解氮质量分数优于四周，且研究区东部土壤水解氮质量分数高于西部；有效磷在研究区内东北部极其缺乏，南部土壤有效磷质量分数高于其他地方，其次是西部有效磷质量分数高于北部；在研究区内，有机质分布较集中且质量分数较高，研究区中部的有机质质量分数高于四周，中部偏东地区有机质丰富；土壤中全氮质量分数东部高于西部，南部高于北部，中部偏南地区土壤全氮质量分数最高。因此，了解不同土壤养分之间的影响因素及其空间联系，对指导毛竹林经营措施，实现毛竹高产具有重要作用。

[1] 程先富,史学正,于东升,等.江西省兴国县土壤全氮和有机质的空间变异及其分布格局[J].应用与环境生物学报,2004,10(1)：64-67.

[2] 孙志虎,王庆成.水曲柳人工林土壤养分的空间异质性研究[J].水土保持学报,2007,21(2)：81-84.

[3] 杜洪业,徐程扬,张添咏.阔叶红松林土壤养分空间异质性地统计学分析[J].东北林业大学学报,2013，41(10)：98-102.

[4] FAGROUDA M, VAN MEIRVENNE M. Accounting for soil apatial auto-correlation in the design of experimental trials[J]. Soil Science,2000,66(4)：1134-1142.

[5] 李艳,史舟,徐建明,等.地统计学在土壤科学中的应用及展望[J].水土保持学报,2003,17(1)：178-182.

[6] WEBSTER R. Quantitative spatial analysis of soil in the field[M]//Springer New York. Advances in Soil Sciences. New York: Springer New York,1985：1-70.

[7] ROBERTSON G P. Geostatistics in ecology： interpolating with known variance[J]. Ecology,1987,68(3)：744-748.

[8] WEBSTER R, OLIVER M A. Optimal interpolation and isarithmic mapping of soil properties. VI. Disjunctive kriging and mapping the conditional porbability[J]. European Journal of Soil Science,1989,40(3)：497-512.

[9] YOST R S, UEHARA G, FOX R L. Geostatistical analysis of soil chemical properties of large land areas．II．Kriging[J]. Soil Science Society of America Journal,1982,46(5)：1033-1037.

[10] 王其兵,李凌浩,刘先华,等.内蒙古锡林河流域草原土壤有机碳及氮素的空间异质性分析[J].植物生态学报,1998,22(5)：409-414.

[11] 刘璐,曾馥平,宋同清,等.喀斯特木论自然保护区土壤养分的空间变异特征[J].应用生态学报,2010,21(7)：1667-1673.

[12] 范少辉,赵建诚,苏文会,等.不同密度毛竹林土壤质量综合评价[J].林业科学,2015,51(10)：1-9.

[13] 郭晓敏,牛德奎,陈防,等.毛竹林平衡施肥与营养管理[M].北京：科学出版社,2013.

[14] 陈冲.海子坪天然毛竹无性系种群地下茎系统研究[D].昆明：西南林学院,2008.

[15] 黄启堂,陈爱玲,贺军.不同毛竹林林地土壤理化性质特征比较[J].福建林学院学报,2006,26(4)：299-302.

[16] 范鲁安,刘萌.对福建省生物防火林带建设的调查与思考[J].森林防火,2015(3)：45-47.

[17] 李宝银.福建省生态公益林经营方案编制技术的研究[J].华东森林经理,2003,17(3)：1-5.

[18] 刘丽,陈双林.有机材料林地覆盖对雷竹林生态系统的负面影响研究综述[J].广西植物,2009,29(3):327-330.

[19] 刘丽,陈双林,李艳红.基于林分结构和竹笋产量的有机材料覆盖雷竹林退化程度评价[J].浙江林学院学报,2010,27(1)：15-21.

[20] 郭子武,陈双林,杨清平,等.雷竹林土壤和叶片N、P化学计量特征对林地覆盖的响应[J].生态学报,2012,32(20)：6361-6368.

[21] 吕真真,刘广明,杨劲松,等.环渤海沿海区域土壤养分空间变异及分布格局[J].土壤学报,2014，51(5):944-952.

[22] 张万儒,杨光滢,屠星南,等.森林土壤分析方法[M].北京：中国标准出版社,2000.

[23] 张文敏,姜小三,吴明,等.杭州湾南岸土壤有机碳空间异质性研究[J].土壤学报,2014,51(5)：1087-1095.

[24] 苏松锦,刘金福,何中声,等.格氏栲天然林土壤养分空间异质性[J].生态学报,2012,32(18)：5673-5682.

[25] 王绍强,朱松丽,成虎.中国土壤土层厚度的空间变异性特征[J].地理研究,2001,20(2)：161-169.

[26] LI H, REYNOLDS J F. On definition and quantification of heteroge-neity[J]. Oikos,1995,73：280-284.

[27] 王军,傅伯杰,邱扬,等.黄土高原小流域土壤养分的空间异质性[J].生态学报,2002,22(8)：1173-1178.

[28] LEGENDRE P, FORTIN M J. Spatial pattern and ecological analysis[J]. Vegetatio,1989,80(2)：107-138.

[29] 林振清.建瓯市毛竹林土壤速效氮磷钾含量及空间分布[J].福建林业科技,2011,38(2)：17-21.

[30] 郭晓敏.毛竹林平衡施肥及营养管理研究[D].南京：南京林业大学,2003.

[31] 曹永慧,萧江华,陈双林,等.竹阔混交林阔叶树下土壤养分对毛竹生长的影响[J].南京林业大学学报(自然科学版),2007,31(6)：43-47.