一类两个自由度Hamilton系统的重整化群方程

孙 宁, 宫万家， 宋 莹

(吉林大学 数学学院, 长春 130012)

0 引 言

重整化理论广泛应用于量子场论和统计物理中, 文献[1-2]通过对电荷、 质量、 耦合常数以及波函数等进行重整化, 巧妙地克服了传统摄动方法的局限性, 把复杂奇异摄动问题的求解转化为一类简单方程----重整化方程的求解问题. 文献[3-5]建立并发展了摄动重整化群方法, 在给出几类重要奇异摄动问题的一致有效渐近展开式的同时, 探讨了重整化群方法与经典奇摄动技巧之间的关系. 目前, 重整化群方法已广泛应用于微分方程等领域, 并取得一系列的成果[6-7].

文献[8-10]利用重整化群方法研究了一类两个自由度的Hamilton系统, 证明了: 如果Hamilton系统的二阶重整群方程是Hamilton系统, 则原Hamilton系统和重整化群方程都是可积的. 文献[8-10]考虑的Hamilton系统为

(1)

其中:ε是小参数; 势能函数V(q1,q2)是q1和q2二次或三次齐次多项式, 得到如下结果:

定理1[8-10]如果Hamilton系统(1)的二阶重整化群方程是Hamilton系统, 则Hamilton系统(1)及其重整化群方程都是可积的.

定理2[11]Hamilton系统(1)的二阶重整化群方程是Hamilton系统当且仅当Hamilton系统(1)是可分的, 即V(q1,q2)关于q1和q2是可分的. 其中: 势能V(q1,q2)是解析函数, 且只含有的q1和q2的偶次项.

本文运用重整化群方法研究一类更一般的两个自由度Hamilton系统, 得出其O(ε)阶重整化群方程, 并证明了该重整化群方程也是Hamilton系统.

1 主要结果

考虑如下两个自由度的Hamilton系统:

其中势能函数V(q1,q2,p1,p2)是解析函数. 与H对应的运动方程组为

(2)

首先, 用求解重整化群方法求方程组(2)的一致有效近似展开式, 主要分如下两步.

1) 求直接摄动展开式.

假设

(3)

将式(3)代入方程组(2)中, 对比等式两端ε的同次幂系数, 得

解式(4)得

(6)

其中B1,B2,C1,C2是任意常数. 由式(5),(6)得

(7)

为求解式(7), 将Uj(q10,q20,p10,p20)和Vj(q10,q20,p10,p20)做Fourier展开, 得

(8)

其中

(9)

将式(8)代入式(7)得

(10)

解式(10)得

(11)

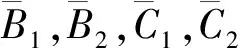
于是, 可得方程组(2)的一阶直接展开式:

(12)

2) 导出重整化群方程.

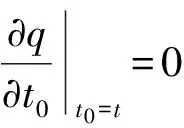
因此, 方程组(2)的O(ε)阶重整化群方程为

(13)

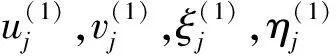
重整化群方程(13)是Hamilton系统. 事实上, 令

直接计算得

综上, 可得:

定理3Hamilton系统(2)的O(ε)阶重整化群方程为

(14)

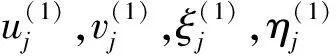
[1] Wilson K G, Kogut J B. The Renormalization Group and the Epsilon Expansion [J]. Phys Rept, 1974, 12(2): 75-200.

[2] Wilson K G. The Renormalization Group: Critical Phenomena and the Kondo Problem [J]. Rev Modern Phys, 1975, 47(4): 773-840.

[3] Goldenfeld N, Martin O, Oono Y. Asymptotics of Partial Differential Equations and the Renormalisation Group [J]. NATO Adv Sci Inst Ser B Phys, 1991, 284: 375-383.

[4] CHEN Linyuan, Goldenfeld N, Oono Y. Renormalization Group Theory for Global Asymptotic Analysis [J]. Phys Rev Lett, 1994, 73(10): 1311-1315.

[5] CHEN Linyuan, Goldenfeld N, Oono Y. Renormalization Group and Singular Perturbations: Multiple Scales, Boundary Layers, and Reductive Perturbation Theory [J]. Phys Rev E, 1996, 54(1): 376-394.

[6] Deville R E L, Harkin A, Holzer M, et al. Analysis of a Renormalization Group Method and Normal Form Theory for Perturbed Ordinary Differential Equations [J]. Phys D, 2008, 237(8): 1029-1052.

[7] 田华, 赵昕, 孙久静. 一类非线性系统的中心流形与重整化群方法 [J]. 吉林大学学报(理学版), 2015, 53(6): 1189-1192. (TIAN Hua, ZHAO Xin, SUN Jiujing. Center Manifold of a Class of Nonlinear Dynamical System and Renormalization Group Method [J]. Journal of Jilin University (Science Edition), 2015, 53(6): 1189-1192.)

[8] Yamaguchi Y Y, Nambu Y. Renormalization Group Equations and Integrability in Hamiltonian Systems [J]. Prog Theor Phys, 1998, 100(1): 199-204.

[9] Yamaguchi Y Y. Second Order Phase Transition in a Highly Chaotic Hamiltonian System with Many Degrees of Freedom [J]. Int J Bif Chaos, 1997, 7(4): 839-847.

[10] Yamaguchi Y Y, Konishi T. A Geometrical Model for Stagnant Motions in Hamiltonian Systems with Many Degrees of Freedom [J]. Prog Theor Phys, 1998, 99(1): 139-144.

[11] Yoshiyuki Y, Yamaguchi Y Y, Nambu Y. Canonical Structure of Renormalization Group Equations and Integrability of Hamiltonian Systems [J/OL]. Physics, 1998-10-07. http://arxiv:chao-dyn/9810010v1.

[12] Kunihiro T. A Geometrical Formulation of the Renormalization Group Method for Global Analysis [J]. Prog Theor Phys, 1995, 94(4): 503-514.