LSTM网络和ARMA模型对惯性器件随机误差预测适应性分析

杨 其， 陈水忠， 沈淑梅， 朱振华

(1.火箭军工程大学,a.士官学院，山东 青州 262500；b.初级指挥学院，西安 710025；2.中国航空工业集团公司洛阳电光设备研究所，河南 洛阳 471000)

0 引言

惯性器件可以在不借助外部信息的孤立系统中直接测量比力和角速率值，因此在飞行器、舰船、智能设备等众多领域得到了广泛应用，同时作为一种自推算制导方式，惯性制导本身也不可避免地存在缺陷，其误差会随时间不断累积并放大。依靠地面静态环境建立误差模型并标定系数，可以在一定程度上对误差进行补偿。但地面标定环境总是与实际工作的动态环境存在一定差别，误差模型也难以对真实误差完全补偿，一般将两者的差距归入随机误差。

造成惯性器件产生随机误差有众多因素[1-5]，按照目前已知的物理原因一般将其分为量化噪声、零偏不稳定性、角度随机游走、速率斜坡等。解决随机误差的最根本方法是对误差来源的物理机制深入研究，提高制造工艺消除误差，但这样的做法不仅导致费效比较高，而且目前对某些惯性器件随机误差成因并未形成统一的结论。例如,惯性器件的零偏不稳定性多认为由电子元件的闪烁噪声导致，但对闪烁噪声形成机理和分析方法仍未形成确定性共识[6-7]。因此，目前对随机误差的补偿方法多基于将各种噪声作为滤波项加入系统方程进行在线实时滤波[8-9]，但滤波方法本质上是一种信号融合工具，需要建立在对实际系统描述基本准确的基础上，不加任何验证直接对滤波系统方程进行扩展极易导致对实际系统的欠拟合，使滤波难以收敛，这也是大量改进形式滤波算法难以实际应用的重要原因。

本文研究主要针对惯性器件随机误差预测问题，对比了成熟的基于时间序列的自回归-滑动平均(Auto-Regressive and Moving Average Model，ARMA)建模方法和流行的深度学习的长短时记忆(Long Short-Term Memory，LSTM)网络在该问题上的适用性和实时预测效率。

1 随机误差ARMA模型拟合局限性分析

按照时间先后顺序记录的一系列惯性器件输出的数据可以作为一个时间序列。由于惯性器件受到各种不确定因素的作用，输出的时间序列中包含各种随机误差，同时惯性器件作为实际存在的物理系统，相邻时间点上的输出会存在状态延续性，可以认为时间序列反映了系统的内在规律，并通过拟合序列建模的方法来预测系统进一步的输出。在无实时性要求情况下，常用方法为建立ARMA模型，即认为惯性器件时间序列y(n)包含了以下分解项

y(n)=f(n)+s(n)+x(n)

(1)

式中,f(n)，s(n)，x(n)分别表示趋势项、周期项和随机项。其中，趋势项提取可采用差分法或最小二乘法，对周期项亦可通过功率谱密度分析并差分去除。ARMA模型主要针对随机项x(n)，并认为当前时刻的测量值与之前的p个测量值、白噪声w(n)以及之前的q个时间平移白噪声w(n-1)，w(n-2)，…，w(n-q)相关，即

(2)

但在工程应用中,惯性器件误差输出最为突出的特征表现为性能可重复性差，即存在一次通电误差和逐次通电误差，因此必须获取足够长的时间样本才能够真实反映惯性器件的特性。假设时间序列样本服从AR(1)模型且时间序列长度为N，可以根据式(2)构建N-1个方程，即

(3)

式中：a1为AR(1)模型参数;w(n)为白噪声。

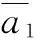
(4)

对式(4)中部分参数进行近似，令

(5)

(6)

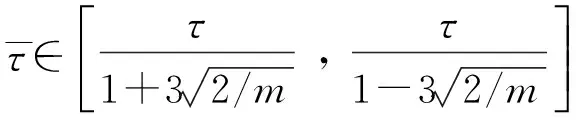
(7)

以某陀螺仪上电输出为例进行时间序列分析，获取长度为500的时间序列(第1组)，如图1所示。

图1 陀螺输出序列样本Fig.1 Original series of gyro output

对获取时间序列逐步回归提取趋势项，其趋势项表达式为

f(t)=59.365 2+68.711 5t-8.375 2t-2-766.356 4t1/2+
667.456 8t-1/2+86.265 7e-t+675.354lnt。

(8)

提取趋势项后的样本序列如图2所示。

图2 提取趋势项后序列样本Fig.2 Time series after extracting the trend term

经功率谱检验，序列中存在的周期项并不显著。对其进行ARMA建模，分别求解自相关函数和偏自相关函数，如图3所示。

图3 自相关和偏自相关函数(第1组)Fig.3 Autocorrelation function and the partial autocorrelation function (Group 1)

时间序列应识别为一阶MA模型，参数估计值为b1=0.731 8。

在同样试验条件下，对同一个陀螺再次上电获取长度为500的时间序列(第2组)，提取趋势项为

f(t)=65.341 5+67.253 4t-6.674 3t-2-638.236 4t1/2+

681.259 1t-1/2+90.300 2e-t+585.567 3lnt

(9)

其自相关函数和偏自相关函数如图4所示。

时间序列识别为一阶MA模型，参数估计值为b1=0.567 1。

两组时间序列拟合后的残差均近似为白噪声，对比如图5所示。

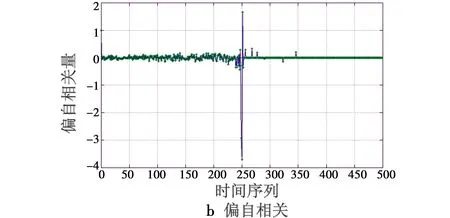
图4 自相关和偏自相关函数(第2组)Fig.4 Autocorrelation function and the partial autocorrelation function (Group 2)

图5 拟合残差(第1组和第2组)Fig.5 The fitting residuals (Group 1 and Group 2)

通过算例对比可以看到，依据不同样本序列对同一个惯性器件建立的ARMA模型在趋势项和模型参数上仍差别较大。由于算例直接获取的时间序列并不长，有可能导致周期性误差未能完全体现，但算例对比足以说明在惯性器件逐次通电误差影响下，即使ARMA模型构建的十分精确，使用该模型对另一组数据的预测效果也并不理想，同时,模型建立的时间序列数据在静态环境中获取，用其拟合动态环境激励出的随机误差结果将更不理想。

2 随机误差预测LSTM网络构建

通过分析可以看到，由于惯性器件本身存在逐次通电误差，时间序列样本相当于在随机过程中提取了一个片段，而且该随机过程的平稳性和遍历性无法确定，对“片段数据”进行高精度的ARMA建模极易导致过拟合，使模型泛化能力下降。而提高预测精度需要付出巨大的时间成本，并集中体现在时间序列样本获取长度上，因此难以应用于实时性要求高的场合。但借鉴其思路，如果能够将建立具体的预测模型替代为建立深度学习网络，事先利用大量的标签数据对其进行训练，不仅可以解决ARMA模型泛化能力不够的问题，而且训练完善的网络在实际使用时具有较高的实时性。

惯性器件作为实际物理系统，当前时刻输出与相邻时刻的输出必然存在一定的相关性，变化规律并不像公共场合客流数据一样存在无穷方参与博弈，出现无规则跳变，因此对惯性器件输出序列的预测采用LSTM网络是一种合适的构建形式，其基本组成单元如图6所示。

图6 LSTM网络基本单元Fig.6 Basic unit of LSTM network

LSTM网络是循环神经网络(RNN)的一种[10-11]，每个基本单元输入xn与前一个单元输出hn-1连接后通过线性单元σ(Sigmoid函数运算)转化为区间[0,1]之间的系数fn，同样tanh单元表示将数值映射到区间[-1,1]之间，这一部分的特征映射表达式为

(10)

式中,Wf,bf,Wi,bi,Wc,bc为待训权重。

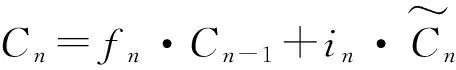
(11)

式(11)实际上包含了“遗忘门”的设计，通过线性叠加确定本次输入信息的权重和对之前信息的遗忘比例[12-14]。遗忘门控单元的设计主要用于控制数据长期依赖性信息的流动，近似于滑动平均的思想：可令αhn-1+(1-α)hn→hn，如果α接近于1,则可以记忆久远地传递信息，而α接近于0,则完全遗忘，防止训练中出现由长期依赖性导致的梯度消失。

基本单元的输出向外的传递系数Cn再次经过一个遗忘门并向同层和其他层传递，即

(12)

将基本单元按照问题的规模和预测输出的长度连接为拓扑结构即可完成网络主要部分的搭建。

3 LSTM网络预测效果对比

LSTM网络实现采用Keras序贯模型(Sequential)，增加多个LSTM网络层接收输入信息并作为隐藏层训练。针对随机误差实时估计，深度学习网络设计目的在于对同一型号的惯性器件能够根据在线敏感到的数据，依靠训练完成的神经网络实时估算即将出现的随机误差，因此在LSTM网络输出时，应根据需要估算的随机误差序列长度的规模设计一个全连接层(Dense)来连接隐藏层和输出层[15-18]。

首先对某陀螺仪获取1000组序列长度为420个时序点的标签样本，在这些样本中既包含多次通电获取到的序列，也包含在一次通电过程中对陀螺仪输出截取获得的序列样本。保留样本的后10组作为预测数据，前990组作为训练样本，首先设计5层LSTM网络进行训练，输入数据按照Keras三维格式组织并全部标准化为区间[0,1]之间数值，选择平均绝对误差百分比(Mean Absolute Percentage Error，MAPE)作为误差比较值。

训练完成后对预测数据的MAPE值为0.270 8，拟合结果与实际数据对比如图7所示。

图7 预测拟合效果对比(5层网络)Fig.7 Comparison of the predicted results of LSTM (5 layers) networks

LSTM网络如需满足惯性器件在线预测的要求，必须具备较高的实时性并能依据较短时间序列完成预测的能力。为了验证网络的实时性，对网络输入输出规模修改后进行在线预测仿真，训练完成后预测结果与实际数据对比如图8所示。

图8 在线实时预测效果对比(5层网络)Fig.8 Online predicted results of LSTM(5 layers) networks

可以看到,由于样本序列缩短却需要预测更远的数据输出，LSTM预测能力出现退化而且预测结果存在延迟。为了改善结果，尝试构建更深的隐藏层，进一步增加LSTM层数至15层，引入Dropout机制概率为0.1，多次对超参数进行调整后，网络对测试样本的拟合以及在线预测结果如图9所示。

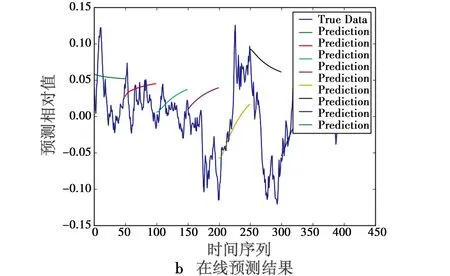
图9 15层LSTM网络预测效果Fig.9 Predicted results of LSTM(15 layers) networks

可以看到,在采用更多LSTM层数时，拟合和预测精度得到了一定的改善。但在线预测过程中由于时间序列规模缩小，预测准确率下降明显,当然准确率下降的原因仍有训练样本不够庞大和参数设置的原因。但通过观察图8、图9，可以看到预测对噪声变化趋势仍保证相当的契合度，仍可以将这个结果作为有色噪声范围对滤波算法进行优化设计。

4 结论

对惯性器件实际应用环境而言，ARMA建模可以提取出惯性器件输出变化的趋势项、周期项并建立其中随机变化部分的自回归滑动平均模型，但需要较长的时间样本和一定规模的计算复杂度，因此方法多应用于不计时效比和实时性的设计、精度验证和工艺提高阶段；而深度学习的LSTM网络通过训练,在样本拟合预测中同样可以达到较好的效果，而且减少了ARMA方法中趋势项和周期项判断，在线实时预测中LSTM网络预测能力会随着时间序列的缩短出现较大的退化，但可以通过叠加更多层LSTM并减小预测输出的规模使预测更为精准，再根据其输出对控制系统的滤波算法进一步优化设计。

[2] MICHAEL A,BLENDER,HEIDI W.Flight dynamics of a hypersonic vehicle during inlet un-start[C]//The 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference,2009:AIAA-2009-7292.

[3] BO W,ZHI H D,CHENG L,et al.Estimation of information sharing error by dynamic deformation between inertial navigation system [J].IEEE Transactions on Industrial Electronics,2014,61(4):2015-2023.

[4] SAVAGE P G.Analytical modeling of sensor quantization in strapdown inertial navigation error equations[J].Journal of Guidance,Control and Dynamics,2002,25(5):833-842.

[5] 张瑞民，杨其，魏诗卉，等.捷联惯测组合标定及误差补偿技术[M].北京：国防工业出版社，2017.

[6] STHAL F,DEVEL M,IMBAUD J,et al.Study on the origin of 1/fnoise in quartz resonators[J].Journal of Statistical Mechanics Theory & Experiment,2016(5):054025.

[7] JONES B K.Electrical noise as a measure of quality and reliability in electronic devices.[J] Advances in Electronics and Electron Physics,1993,87(1):201-257.

[8] BROWN R G,HWANG P Y C.Introduction to random signals and applied Kalman filtering[M].3rd ed.New York:John Wiley & Sons,Inc.,1997.

[9] 韩松来.GPS和捷联惯导组合导航新方法及系统误差补偿方案研究[D].长沙：国防科学技术大学,2010.

[10] HOCHREITER S,SCHMIDHUBER.J.Long short-term memory[J].Neural Computation,1997,9(8):1735-1780.

[11] GERS F A,SCHMIDHUBER J,CUMMINS F.Learning to forget:continual prediction with LSTM[J].Neural Computation,2000,12(10):2451-2471.

[12] HOCHREITER S,BENGIO Y,FRASCONI P.Gradient flow in recurrent nets:the difficulty of learning long-term dependencies[J].Field Guide to Dynamical Recurrent Networks,2001,28(2):237-243.

[13] BENGIO S,BENGIO Y.Taking on the curse of dimensionality in joint distributions using neural networks[J].IEEE Transactions on Neural Networks,Special Issue on Data Mining and Knowledge Discovery,2000,11(3):550-557.

[14] SUTSKEVER I,VINYALS O,LE Q V.Sequence to sequence learning with neural networks[J].Computer Science，2014(4):310-311.

[15] LIPTON Z C,BERKOWITZ J.A critical review of recurrent neural networks for sequence learning[J].Computer Science，2015(1):104-112.

[16] HASIM S,ANDREW S,FRANCOISE B.Long short-term memory current neural networks architecture for large scale acoustic modeling[C]//Proceeding of Interspeech, ISCA,2014:338-342.

[17] GRAVE A.Generating sequences with recurrent neural networks[J].Computer Science,2013(1):234-243.

[18] PALANGI H,DENG L,SHEN Y,et al.Deep sentence embedding using long short-term memory networks:analysis and application to information retrieval[J].IEEE/ACM Transactions on Audio Speech & Language Processing, 2015,24(4):694-707.