基于神经网络的烈度衰减融合模型研究
胡 旺,张 建,陈维锋,胡 斌,郭红梅
(1.电子科技大学计算机科学与工程学院 成都 611731;2.四川省地震局 成都 610041)
地震是造成我国人员死亡最多的自然灾害。地震对某地区地面及建筑屋的破坏程度通常以地震烈度表示,而地震烈度衰减关系在地震灾情分析和震后损失快速评估中起着重要的作用。一次破坏性地震发生后,根据地震三要素即地震发生时间、震级、震中的经纬度在地图上快速定位,并标定地震烈度等震线,确定受灾范围的大小[1]。确定地震烈度等震线的关键要素有3个:震中位置、长轴的方向(与发震断层的破裂方向密切相关)、各烈度圈长轴和短轴半径长度[2]。
川滇地区是我国地震频发区,近年来发生的一些地震,如2008年汶川8.0级地震、2013年芦山7.0级地震、2014年鲁甸6.5级地震,造成的人员损失以及经济损失巨大。因此,对于川滇地区的地震烈度衰减关系的研究具有重大意义。许多专家学者针对我国不同地区建立了不同的地震烈度衰减关系。文献[3]统计了256个地震资料,将中国分为东西部并分别拟合出了烈度衰减关系;文献[4]统计了华北地区37次地震的89条等震线数据,得到了华北地区的烈度衰减关系;文献[5]对新疆地区的103个地震进行统计分析,得到了新疆地区烈度衰减关系。这些烈度衰减关系在一定程度上反映了各地区的烈度衰减关系,但同时也存在着问题。文献[1]用震级M≥6.0的地震事件,以传统烈度衰减模型预测的震害面积与实际观测震害面积比较时发现:在高烈度区,模型预测的震害面积往往比实际观测的震害面积偏小;而在低烈度区,模型预测的震害面积往往比实际观测的震害面积偏大。为此文献[1]对地震烈度衰减模型进行了改进,建立了地震烈度衰减的矩阵模型,该模型在预测精度上有较好的提升。本文在整理分析川滇地区地震等震线资料时,利用中国西部烈度衰减关系[3](M1)和矩阵烈度衰减关系[1](M2)分别预测出收集到的20个地震案例(40条等震线)对应的长轴长度和短轴长度,并计算了每条预测等震线长短轴长度与实际观测等震线长短轴长度的相对误差,在长轴方向上,M2的预测效果好于M1,而在短轴方向上,M1的预测效果则好于M2。文献[3]在建立统计回归的烈度衰减关系M1时,将地震案例数据按照地域进行了分区,考虑了中国东部和西部不同的地质构造和断裂分布的差异。而文献[1]建立的M2则是从地震案例数据的震级因素建立分段统计回归的烈度衰减关系,没有考虑不同地区的地质构造对预测结果造成的影响。因此,本文尝试通过人工神经网络(artificial neural network, ANN)的方法来学习融合M1和M2的优点,从而建立一个具有更好精度的地震烈度衰减融合预测模型。
不同地区的烈度衰减关系存在一定的差异性[3,6,8],而这种差异一般在该地区的历史地震数据中得到体现。M1和M2对川滇地区的烈度衰减关系具有一般的适用性。为发挥两种烈度衰减模型的各自优势特征,本文收集了川滇及邻区110个地震(共250条等震线),利用BP神经网络将两种不同的烈度衰减模型对地震案例预测结果进行学习融合,其中用于烈度衰减融合模型学习的地震案例有101个(共233条等震线),用于烈度衰减融合模型测试验证的地震案例数为9个(共17条等震线)。仿真结果表明,本文建立的地震烈度衰减融合预测模型的准确性在总体上优于中国西部烈度衰减关系和矩阵烈度衰减关系。
1 烈度衰减模型
1.1 中国西部烈度衰减关系
对于我国烈度衰减关系的研究,文献[3]利用我国丰富的地震烈度等震线资料,大致以东经105°将我国烈度衰减关系分为东西部,并采用椭圆长、短轴联合衰减模型[7]回归分析了我国东西部适用的烈度衰减关系。其中,中国西部烈度衰减模型的长轴公式和短轴公式分别为:
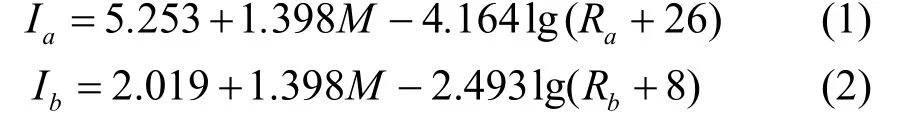
式中,I为地震烈度;M为震级;R为震中距(km);下标a和b分别代表长轴和短轴。式(1)和式(2)的标准差σ=0.632。该模型早已被广泛应用于工程抗震设防研究。
1.2 矩阵衰减模型
为了进一步提高烈度衰减模型预测的精确性,文献[1]认为每一条等震线都仅由衰减公式中的3个系数确定,彼此之间互相耦合,不可避免的缩小了高烈度区面积,放大了低烈度区面积。为此对椭圆衰减模型进行了改进,建立了等震线长轴半径和短轴半径长度矩阵,称之为地震烈度衰减矩阵模型,如表1所示,表中M为震级。
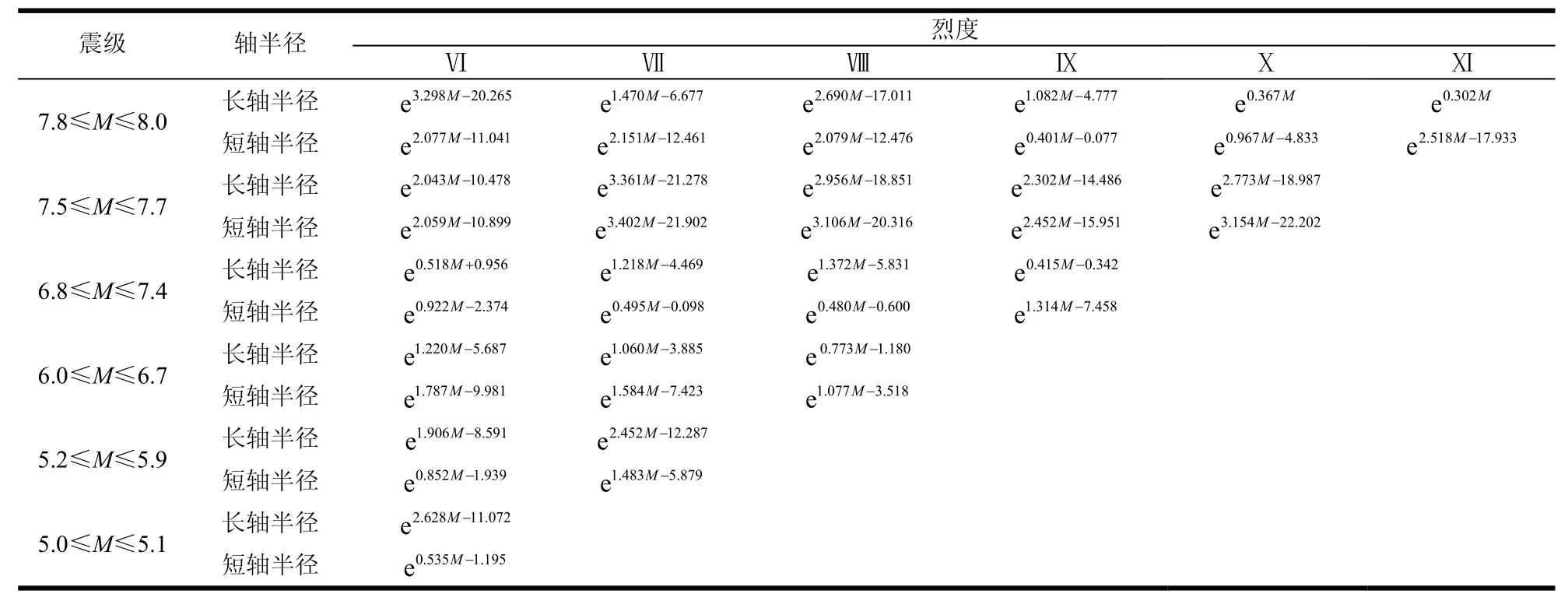
表1 等震线长短轴初始值
2 数据来源及分布
本文所使用数据选取自《中国震例》(1966~1975年,1976~1980年,1981~1985年,1986~1988年,1989~1991年,1992~1994年,1995~199 6年,1997~1999年)、《中国大陆地震灾害损失评估汇编》(1996~2000年,2001~2005年)、2005年以后的相关地震资料及已发表论文中的地震数据[8-13]。2013年后的数据获取方式为:根据国家地震局发布的地震烈度图,将烈度图在ArcMap上地理配准,选取各烈度圈上距离最远的两点连线为长轴,利用地图测量工具及比例尺计算长轴长度;选取各烈度圈垂直于长轴方向的两点连线为短轴,同理计算短轴长度。在以上数据来源中选取川滇地区5.0级以上且震中烈度大于等于6度的地震共107个,243条等震线,其中9个地震共17条等震线用于测试神经网络融合预测模型。由于篇幅限制,表2仅列举川滇及邻区部分地震案例数据。地震案例震级的统计分布如表3所示。
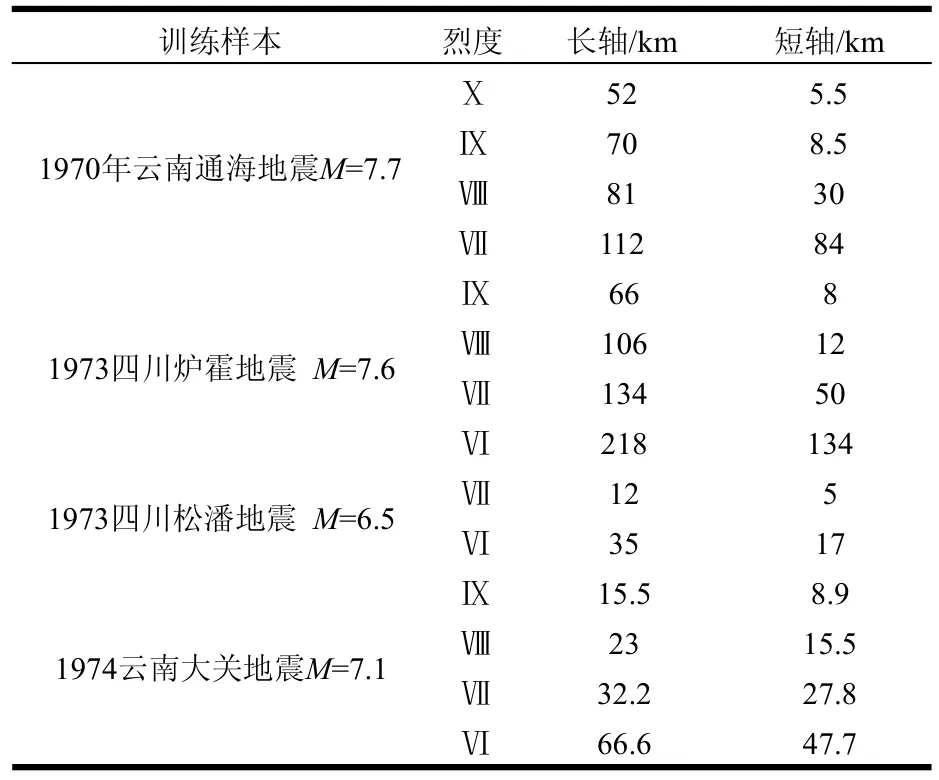
表2 川滇及邻区部分地震案例数据

表3 地震震级分布表
3 基于BP神经网络的融合模型
BP神经网络是一种按信息正向传播和误差反向传播算法训练的多层前馈网络,由Rumelhart和McCelland为首的科学家小组于1986年首次提出,是目前应用最广泛的神经网络模型。BP神经网络采用的学习规则是最快下降法,通过误差的反向传播不断地调整网络的权值和阀值,从而使网络的误差平方和最小[14]。BP神经网络是一个分层拓扑结构,可以分为输入层(input layer)、隐含层(hide layer)和输出层(output layer)。一个3层的BP神经网络可以完成任意n维到m维的函数映射。
本文采用3层BP神经网络建立川滇地区适用的地震烈度衰减融合预测模型(M3)。由于本文的目的是学习融合地震烈度衰减模型M1和M2的优点,并且地震等烈度线的长轴和短轴之间相互关联,因此训练网络时将M1和M2的长轴长度和短轴长度放在同一个神经网络中进行学习训练。本文以地震震级、烈度、M1的长轴和短轴预测值、M2的长轴和短轴预测值作为6个输入节点,以神经网络融合烈度预测模型的长轴长度和短轴长度作为2个输出节点。
在BP神经网络中,输入层和输出层的节点个数都是确定的,而隐含层节点个数不确定。隐层节点数的多少对网络性能的影响较大。当隐层节点太多时,会导致网络学习时间过长,造成过训练[15-16];而当隐层节点数过小时,网络的训练和预测精度较差。本文按照如下思路选取确定神经网络参数:首先根据经验规则确定出隐含层节点数的取值范围,然后在该取值范围内采用试探方法逐一训练网络,最后网络训练误差选定网络效果最好的隐含层节点参数值。本文中隐层节点数取值范围采用经验公式(n2为隐层节点数,n3为输出层节点数,确定,可以估算出隐层节点数为3~12。根据对本文案例数据实际学习训练过程中的误差变化情况,将隐层节点数目确定为12。学习速率的大小对收敛速度和训练结果影响很大。如果学习速率太小,收敛速度变慢;如果学习速率太大,可能导致震荡或发散。综合考虑收敛速度和训练误差,取学习速率lr=0.05;而对于训练精度,取goal=0.000 1,学习训练最大迭代次数tr=1 000次。为了消除输入输出数据量纲不同、数据差异太大带来的影响,对待输入数据进行了归一化处理。根据预处理后的数据范围,网络隐含层神经元变换函数采用tansig函数,输出层采用logsig函数。在网络初始化阶段,采用二进制遗传算法优化初值权值和阀值,使得神经网络比随机初始化方法具有更好的初始状态,遗传算法的参数设置如下:种群规模为100,最大进化代数为1 000,交叉概率为0.75,变异概率为0.01。在迭代学习阶段,需要通过计算神经网络误差来迭代调整所有连接权值和阀值,使得式(3)中系统的平均误差达到最小:
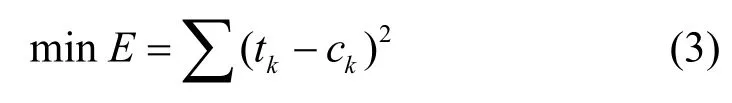
式中,E为误差平方和;tk为计算的输出量;ck为实际的输出量;m为样本数,k=1,2,…,m[20]。
Levenberg-Marquardt(L-M)算法[19]是介于牛顿法与梯度下降法之间的一种非线性优化方法,它通过自适应调整阻尼因子来达到收敛特性,具有更高的迭代收敛速度,综合了梯度下降法和高斯-牛顿方法的优点,具有高斯-牛顿法的局部收敛性和梯度下降法的全局特性,在一定程度上克服了BP神经网络收敛速度慢和容易陷入局部最小点等问题,因此本文采用L-M算法作为神经网络误差迭代优化方法。为了避免过度拟合,在训练时采用随时终止法,即误差达到要求时终止网络训练。
本文建立的BP神经网络模型结构如图1所示,基于BP神经网络的烈度衰减融合预测方法如算法1所示。
算法1:基于神经网络的地震烈度衰减融合算法
1)利用所有的等震线数据,通过式(1)和式(2)计算出M1的每条等震线长轴和短轴预测值;
2)利用所用的等震线数据,通过表1计算出M2的每条等震线长轴和短轴预测值;
3)对所有等震线的震级、烈度以及M1、M2对应的长轴和短轴预测值进行归一化处理;
4)利用遗传算法优化网络初始权值和阀值;
5)For 所有训练样本
计算隐层和输出层的输出;
计算各层的误差值;
按式(3)修正各层的权值和阀值;
计算神经网络的全局误差E;
若E小于goal或训练次数大于tr,则终止训练;End For
本文从地域分布和震级大小分布角度考虑,抽取了9个未用于学习训练的地震案例样本(17条等震线)测试验证训练后的神经网络融合模型的预测效果。将17组仿真样本数据分别用M1和M2对应的公式求出每组样本的长轴和短轴长度,并代入训练好的神经网络中,得到M3相对应的长轴和短轴长度值。3种模型的长轴和短轴预测值及相对误差如表4和表5所示。可以看出,3种模型预测值的相对误差都比较大,这是由地震作用的不确定性以及离散性较大造成的。地震的不确定性决定了比较各个模型的优劣时,不能单独比较各个模型的误差,而应该从样本整体出发,计算仿真样本的总体误差。为了验证各个模型的有效性,选择式(4)中的平均相对误差作为评价指标体系:
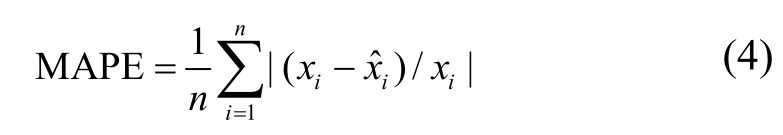
为了更进一步观察分析3种模型预测值误差的分布,M1、M2和M3在9个验证测试地震案例上的相对误差箱形图如图2所示。
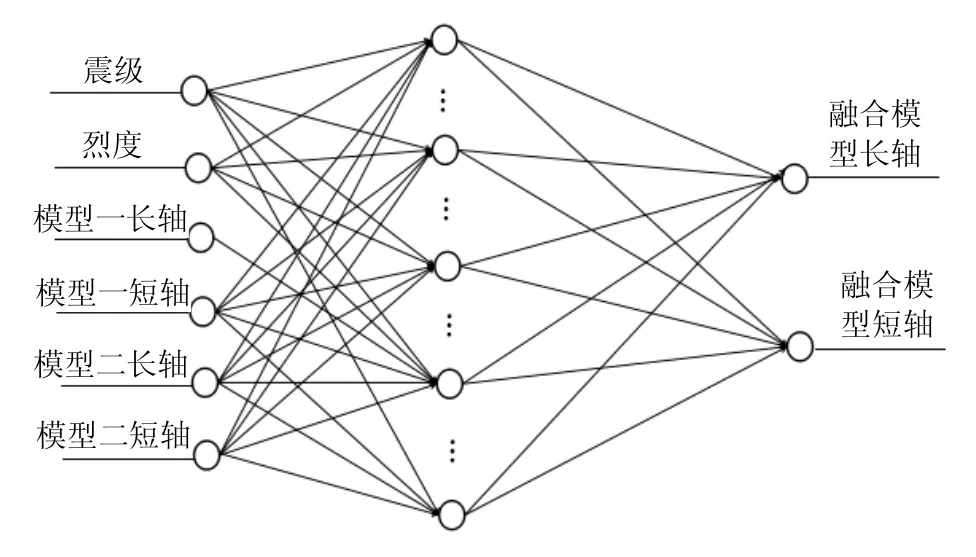
图1 融合预测模型的BP神经网络模型结构
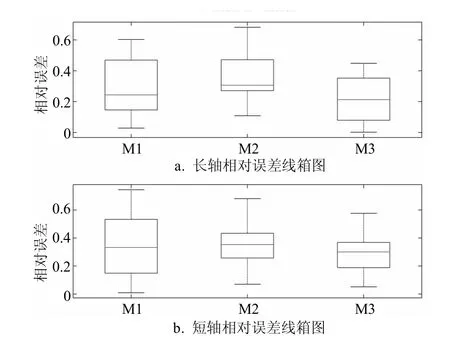
图2 相对误差箱形图
根据表5和图2,从地震烈度衰减模型预测平均误差角度分析,M1在长轴和短轴上的平均预测误差分别为28.77%和34.47%,M2在长轴和短轴上的平均预测误差分别为36.85%和34.49%, 而神经网络融合预测模型M3在长轴和短轴上的平均预测误差分别为20.90%和28.85%。M3在长轴上的平均预测精度分别比M1和M2提升了7.87%和15.95%,M3在短轴上的平均预测精度分别比M1和M2提升了5.62%和5.64%。因此,无论在长轴或短轴方向上的平均预测误差,M3的预测效果总体上要优于M1和M2。

表4 3种模型的长轴预测值和相对误差
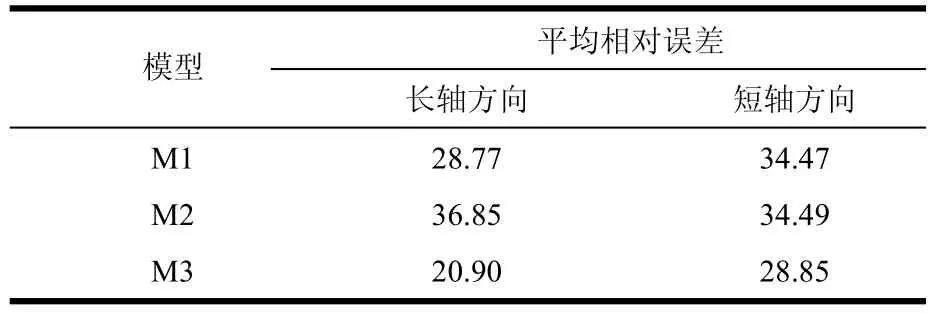
表5 3种模型的相对误差
4 结束语
本文收集了川滇及邻区的101个地震案例(233条等震线),利用BP神经网络将M1与M2进行了学习融合,得到的融合预测模型对川滇地区的椭圆烈度衰减模型长短轴的计算具有一定的参考价值。仿真测试结果表明,融合预测模型的预测精确度在总体上优于M1和M2。利用BP神经网络得到的融合预测模型提高了地震烈度衰减预测值的精确度。但神经网络在地震案例数据覆盖区域内具有较好的预测效果,而对地震案例未覆盖区域的预测则效果欠佳。下一步的工作是收集更广泛且有仪器记录的地震案例,利用数理统计的方法选取覆盖范围广和分布均匀的地震案例用于神经网络的融合学习,从而进一步提高神经网络融合预测模型的预测精度。
[1]许卫晓.烈度分布快速评估方法研究[D].哈尔滨: 中国地震局工程力学研究所, 2011.XU Wei-xiao.The study of methods for rapid assessment of seismic intensity distribution[D].Harbin: Institute of Engineering Mechanics, China Earthquake Administration,2011.
[3]王景来, 宋志峰.地震灾害快速评估模型[J].地震研究,2001, 24(2): 162-167.WANG Jing-lai, SONG Zhi-feng.Model for fast seismic disaster assessment[J].Journal of Seismological Research,2001, 24(2): 162-167.
[3]汪素云, 俞言祥, 高阿甲.中国分区地震动衰减关系的确定[J].中国地震, 2000, 16(2): 99-106.WANG Su-yun, YU Yan-xiang, GAO A-jia.Development of attenuation relations for ground motion in China[J].Earthquake Research in China, 2000, 16(2): 99-106.
[4]崔鑫, 苗庆杰.华北地区地震烈度衰减模型的建立[J].华北地震科学, 2010, 28(6): 18-21.CUI Xin, MIAO Qing-jie.Model of the seismic intensity attenuation for north China[J].North China Earthquake Sciences, 2010, 28(6):18-21.
[5]TAN Ming, LI Shuai, SUN Jing, et al.Parameter fitting of seismic intensity attenuation model in Xinjiang[J].Earthquake Research in China, 2013, 27(2): 261-268.
[6]白仙富, 戴雨芡, 赵恒.地震影响场应急评估方法研究[J].自然灾害学报, 2014, 23(4): 91-102.BAI Xian-fu, DAI Yu-qian, ZHAO Heng.Study on the emergency evaluation of earthquake influence field[J].Journal of Natural Disasters, 2014, 23(4): 91-102.
[7]陈达生, 刘汉生.地震烈度椭圆衰减关系[J].华北地震科学, 1989, 7(3): 31-42.CHEN Da-sheng, LIU Han-sheng.Elliptical attenuation relationship of earthquake intensity[J].North China Earthquake Sciences, 1989, 7(3): 31-42.
[8]孙继浩.川滇及邻区中强地震烈度衰减关系的适用性研究[D].北京: 中国地震局地震预测研究所, 2011.SUN Ji-hao.Study of moderate-strong seismic intensity attenuation relations in sichuan-yunnan and its adjacent areas[D].Beijing: Institute of Earthquake Science China Earthquake Administration, 2011.
[9]常银辉.基于断层距的地震烈度衰减关系研究[D].哈尔滨: 中国地震局工程力学研究所, 2012.CHANG Yin-hui.Research on attenuation relationship of seismic intensity based on fault distance[D].Harbin:Institute of Engineering Mechanics, China Earthquake Administration, 2012.
[10]周中红, 何少林.甘肃省地震烈度衰减关系研究[J].西北地震学报, 2010, 32(1): 72-75.ZHOU Zhong-hong, HE Shao-lin.Study on the attenuation relationship of seismic intensity in gansu province[J].Northwestern Seismological Journal, 2010, 32(1): 72-75.
[11]肖亮, 俞言祥.中国西部地区地震烈度衰减关系[J].赈灾防御技术, 2011, 6(4): 358-371.XIAO Liang, YU Yan-xiang.Earthquake intensity attenuation relationship in western China[J].Technology for Earthquake Disaster Prevention, 2011, 6(4): 358-371.
[12]龙德雄, 吴今生, 王松.2005年8月5日云南省会泽-四川省会东5.3级地震四川震区地震烈度宏观考察[J].四川地震, 2006, 1(1): 1-8.LONG De-xiong, WU Jin-sheng, WANG-Song.The macro disaster investigating on the Ms5.3 Huize-Huidong earthquake on 5 august 8 2005[J].Earthquake Research in Sichuan, 2006, 1(1): 1-8.
[13]常祖峰, 张艳凤, 周青云.2013年洱源Ms5.5地震烈度分布及震区活动构造背景研究[J].中国地震, 2014, 30(4):560-570.CHANG Zu-feng, ZHANG Yang-feng, ZHOU Qin-yun.Intensity distribution characteristics and active tectonic background in area of the 2013 Eryuan Ms5.5 earthquake[J].Earthquake Research in China, 2014, 30(4):560-570.
[14]戴超杰, 刘媛华.基于改进的BP神经网络库存预测模型研究[J].物流科技, 2015(11): 26-30.DAI Chao-jie, LIU Yuan-hua.Research on inventory forecasting model based on improved BP neural network[J].Logistics Sci-Tech, 2015(11): 26-30.
[15]SUN Jian-ye.Learning algorithm and hidden node selection scheme for local coupled feedforward neural network classifier[J].Neurocomputing, 2012, 79: 158-163.
[16]CHOI B, LEE J H, KIM D H.Solving local minima problem with large number of hidden nodes on two-layered feed-forward artificial neural networks[J].Neurocomputing,2008, 71(16-18): 3640-3643.
[17]高大启.有教师的线性基本函数前向三层神经网络结构研究[J].计算机学报, 1998, 21(1): 80-86.GAO Da-qi.On structures of supervised liner basis function feed-forward three-layered neural networks[J].Chinese Journal of Computers, 1998, 21(1): 80-86.
[18]MIRCHANDANI G, WEI C.On hidden nodes for neural nets[J].IEEE Trans on Circuits and Systems, 1992, 36(5):661-664.
[19]MCKEOWN J J, STELLA F, HALL G.Some numerical aspects of the training problem for feed-forward neural nets[J].Neural Networks, 1997, 10(9): 1455-1463.
[20]胡旺, 李志蜀.基于回归和神经网络的NdFeB磁性能融合预测模型[J].四川大学学报(工程科学版), 2004, 36(6):66-69.HU Wang, LI Zhi-shu.A fusion prediction model based on regression and neural network for nano-composite NdFeB permanent magnet alloy[J].Journal of Sichuan University(Engineering Science Edition), 2004, 36(6): 66-69.
[21]李静文, 刘刚.基于BP神经网络的景气预测模型[J].统计与决策, 2015(32): 70-74.LI Jing-wen, LIU Gang.Boom forecasting model based on BP neural network[J].Statistics and Decision, 2015(32):70-74.

