有色金属国际期货市场价格联动效应演化分析——以铜、铝、锌为例

董晓娟，安海岗，董志良

(河北地质大学管理科学与工程学院，石家庄 050031)

0 引言

从全球来看，中国是有色金属的最大生产国和消费国。在中国，铜、铝、锌等有色金属应用十分广泛，尤其是涉及交通运输、电力、建筑等基础行业，也是期货投资的一大热点。而近几年有色金属价格的强烈波动给有色金属的投资带来了巨大的影响，加大了其交易风险。为了降低有色金属投资风险，有必要进行分散投资。而降低风险的成效如何，与分散投资的期货品种组合选择有很大关系。期货品种组合不同，其价格联动关系的差异会直接导致其对风险降低的效果的不同。因此，本文以铜、铝、锌3种最主要的有色金属为例，分析3种有色金属两两之间的关系，通过引入复杂网络建模方法，对时间序列上3种有色金属价格两两关联的联动效应随时间演化的特征进行分析，最终提出铜、铝、锌3种有色金属价格联动效应的演化规律，并对有色金属的期货投资提出了建议。

1 相关研究综述

以往多个学者虽然提出了各种建网方法，但在基于两个以上时间序列变量建网的过程中为了建网的方便，大多忽略了时间序列之间关系的部分细节，如可视图方法、粗粒化方法。而基于回归模型建网的方法对于从细节上分析时间序列之间的关系模式有很大帮助。因此，本文拟基于回归模型建立复杂网络，进而分析时间序列之间波动相关关系细节。

2 数据和方法

2.1 数据

本文选取的数据来自Wind数据库，选取2008年1月3日至2018年9月18日的伦敦金属交易所(LME)的铜、铝、锌3个月期货收盘价作为样本数据，获取2 707组数据作为样本。通过相关性分析发现，铜、铝的Pearson相关系数为0.777，在0.01水平上显著相关；铜、锌的Pearson相关系数为0.340，在0.01水平上显著相关；铝、锌的Pearson相关系数为0.366，在0.01水平上显著相关。

2.2 数据处理

2.2.1 平稳性检验

首先，对铜、铝、锌3个月期货价格时间序列数据取对数后进行平稳性检验。设变量x、y、z分别为对铜、铝、锌3个月期货收盘价取其自然对数的时间序列变量。

分别对x、y、z使用ADF(Augmented Dickey-Fuller)检验进行平稳性检验，结果如表1所示。其中，x1、y1、z1分别表示x、y、z的一阶差分变量。x、y、z为不平稳时间序列，而其一阶差分时间序列为平稳时间序列。

表1 时间序列x, y, z的ADF检验结果

接下来对x、y、z使用PP(Phillips-Perron)检验再次进行平稳性检验，结果如表2所示。

表2 时间序列变量x, y, z 的PP检验结果

对比ADF检验结果和PP检验结果，x、y、z均为一阶单整时间序列。

2.2.2 协整检验

运用Johansen Cointegration Test进行协整检验。检验结果如下：x和y“不存在协整关系”的假设P值为0.011 6，小于0.05的显著性水平，说明x和y两个时间序列存在协整关系；x和z“不存在协整关系”的假设P值为0.131 3，大于0.1的显著性水平，说明两个时间序列x和z不存在协整关系；y和z“不存在协整关系”的假设P值为0.000 6，小于0.05的显著性水平，说明时间序列y和z存在协整关系。这说明铜和铝、铝和锌期货价格之间存在长期稳定的均衡关系和相互影响。

2.2.3 格兰杰因果检验。

建立x和y的VAR(向量自回归)模型，确定最优滞后阶数为7。然后进行格兰杰因果检验，对于原假设“y不是x的格兰杰原因”，P值为0.005 5，在0.05的显著性水平上，拒绝原假设；对于原假设“x不是y的格兰杰原因”，P值为0.005 3，在0.05显著性水平上拒绝原假设，因此x和y互为格兰杰因果。

建立y和z的VAR(向量自回归)模型，确定最优滞后阶数为7。然后进行格兰杰因果检验，对于原假设“z不是y的格兰杰原因”，P值为0.083 6，在0.05的显著性水平上，接受原假设；对于原假设“y不是z的格兰杰原因”，P值为9×10-7，在0.05显著性水平上拒绝原假设，因此选择y作为解释变量，z为被解释变量。为测算方便，在后面建立回归模型时，都选择y作为解释变量。

2.2.4 建立回归模型

首先，分别建立铜和铝、铝和锌价格对数的差分时间序列x1、y1、z1的回归模型。模型方程为

xt=cx+αyt+μt

(1)

zt=cz+βyt+εt

(2)

其中，xt为铜价格对数的差分时间序列，yt为铝价格对数的差分时间序列，zt为锌价格对数的差分时间序列。α、β为回归系数，cx、cz为常数项，其中回归系数更能代表两个时间序列之间的关系，因此选择回归系数作为关系模式的标志。

(3)

(4)

因为选择的是3个月期货收盘价，因此设滑动时间窗长度为δ，其阈值为[5,75]，5代表每周的交易天数，75为3个月的交易天数。以区间[5,75]内所有值分别依次作为滑动时间窗长度，以步长为1，对时间序列进行回归估计，铜和铝期货价格回归分析示意图如图1所示，铝和锌期货价格回归分析示意图如图2所示。

图1 铜和铝期货价格回归分析示意图

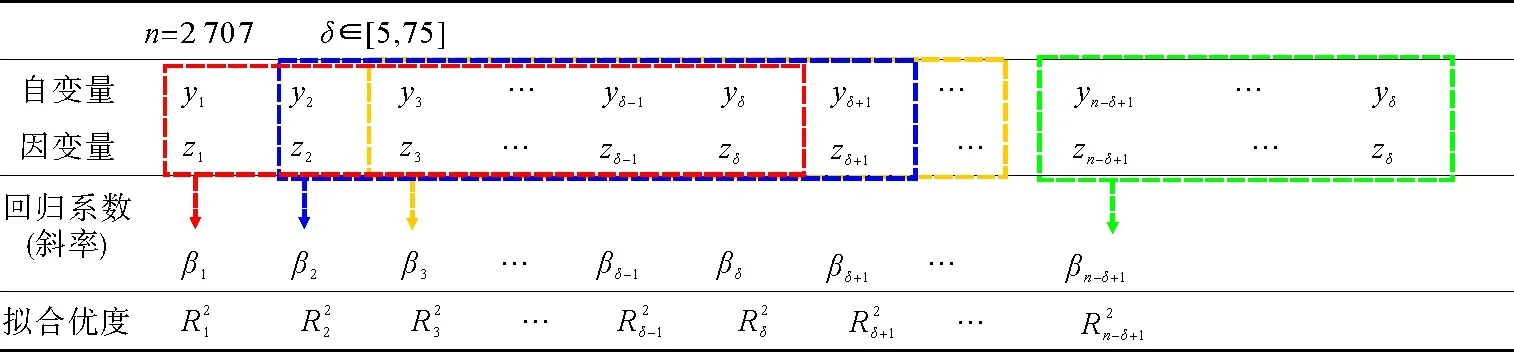
图2 铝和锌期货价格回归分析示意图

接下来，进行最佳时间窗长度的选择和显著性检验。

1)选择最优时间窗长度。

比较铜和铝期货价格所有回归系数的拟合优度的中位数，拟合优度比较图如图3所示。选择其中取值最大的拟合优度中位数对应的δ值作为滑动时间窗长度。因此将拟合优度中位数最大值对应的滑动时间窗长度δ暂定为68。

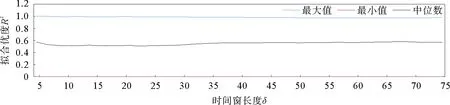
图3 铜和铝期货价格回归分析拟合优度比较图

然后比较铝和锌期货价格所有回归系数的拟合优度的中位数，拟合优度比较图如图4所示。选择其中取值最大的拟合优度中位数对应的δ值作为滑动时间窗长度。将拟合优度中位数最大值对应的滑动时间窗长度δ暂定为5。

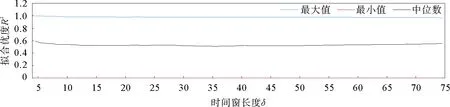
图4 铝和锌期货价格回归分析拟合优度比较图

2)显著性检验

分别对铜和铝时间序列、铝和锌时间序列所有的回归系数进行显著性检验。

对于参数α，在2 686个P值中，有605个P值大于0.05，占总数的22.52%，而小于0.05的P值占比77.48%，大多数回归方程回归系数α通过显著性检验，绘制散点图如图5。

对于参数，在2 704个P值中，有1 798个P值大于0.05，占总数的66.49%，而小于0.05的P值占比33.51%，大多数回归方程回归系数未通过显著性检验。调整时间窗长度δ按拟合优度中位数从大到小的标准依次进行回归系数显著性检验，直到找到显著性检验结果较好的时间窗长度δ。δ依次取值6、7、75，当δ取值6和7时，结果均是1 550个P值大于0.05，超过半数的回归方程回归系数β未通过显著性检验。当δ取值75时，2 633个P值中，有227个P值大于0.05，仅占比8.62%，最后选定时间窗长度δ为75，绘制散点图如图6。

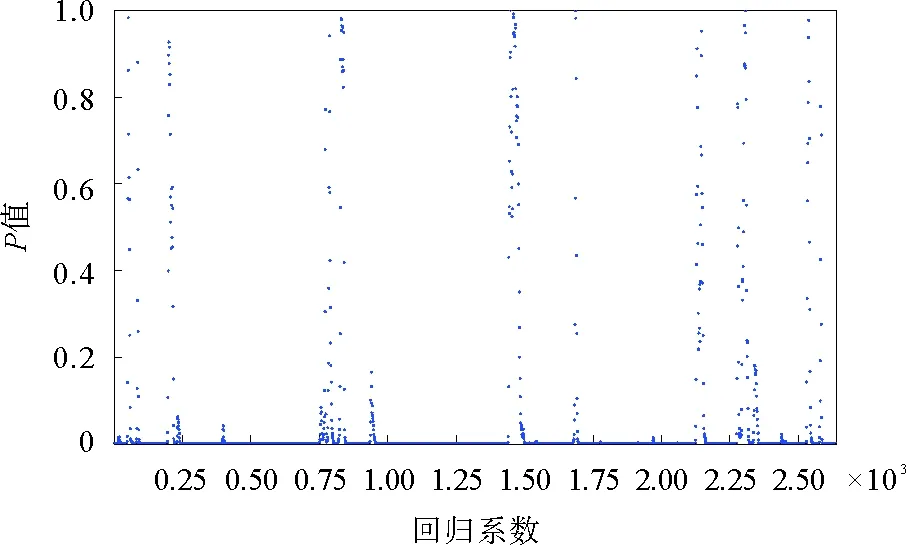
图5 回归系数α显著性检验结果

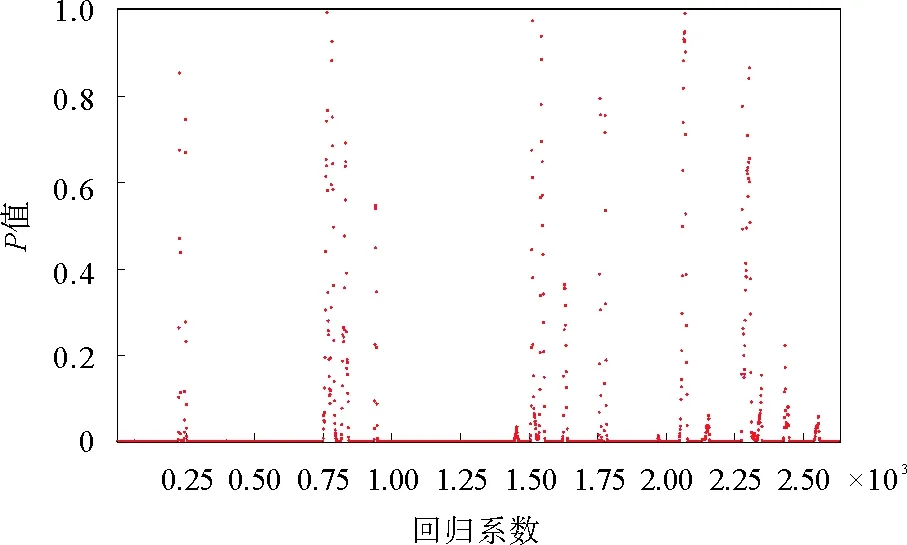
图6 回归系数β显著性检验结果

2.2.5 构建复杂网络模型

对回归系数进行处理。由于回归系数α,β分别代表铜和铝、铝和锌的直接关系，因此其值的高低反映了一种有色金属的波动对另一种有色金属波动的影响。将α以0.1作为区间长度，取其区间长度作为复杂网络中的节点，如[0.6,0.7)，代表铜和铝期货价格时间序列的一种关联模态，网络中的节点数代表了关联模态的总数，即在这种区间划分方法下铜和铝之间的关系类别数。以模态和模态之间的转换作为复杂网络中的边，如[0.7,0.8)→[0.6,0.7)。构建复杂网络如图7。

将同样以0.1作为区间长度，取其区间长度作为复杂网络中的节点，即铝和锌的一种关联模态，网络中的节点数代表了关联模态的总数，即在这种区间划分方法下铝和锌之间的关系类别数。同样以模态和模态之间的转换作为复杂网络中的边。构建复杂网络如图8。

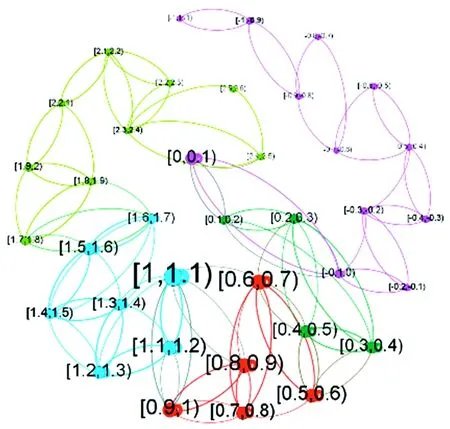
图7 铜和铝期货价格波动关联网络

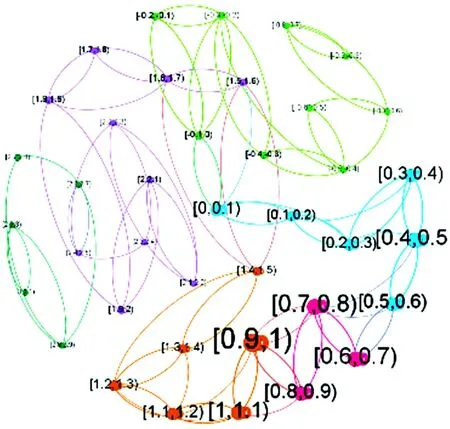
图8 铝和锌期货价格波动相关网络

3 结果

在对时间序列之间的关系进行分析的方法中，直接使用相关系数分析也是较为常见的方法。相关系数分析对于分析时间序列变量之间的整体关联性较为有效，但是在较长时间，两个时间序列之间的关系模式会随着时间发生演化。在分析时间序列之间随时间演化的动力学特征方面，复杂网络方法更为有效。而以往常用的粗粒化方法在反映时间序列之间的关系时，忽略了二者真正关系的细节，而复杂网络和线性回归相结合的方法可以从细节上分析时间序列关系演化的动力学特征。

通过网络分析发现，铜和铝价格波动相关网络节点数为37个，共有143条边。铜铝期货价格波动相关网络中的节点代表铜和铝在时间序列上的关系模式，说明铜和铝在滑动窗长度取68时共有37种关系模式。边代表一种关系模式向另一种关系模式的转换类型数，即铜和铝关系模式之间的转换类型共有143种。该复杂网络为有向加权网络，网络直径为23，平均路径长度为6.676。平均路径长度代表网络中所有节点对之间的平均最短距离。由于建网时滑动时间窗步长设为1天，因此节点到节点的距离即一种关系模式到另一种模式的转换天数。节点对的距离即铜和铝的两种关系模式的转换天数，因此铜和铝关系模式的平均最短转换天数是6～7天。网络直径是所有节点的最大距离，即代表铜和铝的关系模式最长的转换天数为23天。

经过分析发现，铝和锌价格波动相关网络节点数为39个，共有123条边。这说明铝和锌在滑动窗长度取75时共有39种关系模式。而铝和锌关系模式之间的转换类型共有123种。网络直径为25，平均路径长度为8.19。铝和锌关系模式的平均最短转换天数是8～9天。铝和锌关系模式最长的转换天数为25天。

经过对比发现，铜和铝的关系模式种类略少于铝和锌的关系模式，但关系模式之间的转换类型数却多于铝和锌的关系模式转换类型，因此铜和铝的关系模式转换略频繁于铝和锌的关系模式转换，从平均转换天数和最长转换天数也可以从另一个侧面印证这一结论。

3.1 度分布分析

对于有向网络，出度代表某一节点指向其他节点的边数，也代表期货关系模式向另一种模式转换的次数。无论是在铜铝期货价格波动相关网络中还是铝锌期货价格波动相关网络中，除了第一个节点和最后一个节点外，其他节点的出度和入度是相同的，因此以出度为例进行分析。铜和铝、铝和锌期货价格波动相关网络均为有向加权网络，边的权重设为aij，代表一种关系模式到另一种特定关系模式重复转换的次数。设i,j分别为网络中任意一个节点，n为网络中的节点数，aij表示节点i到j的边权。其加权出度p(k)定义为

(5)

分别对铜铝、铝锌期货价格波动相关网络的节点加权出度累积分布进行分析，结果如图9和图10所示。

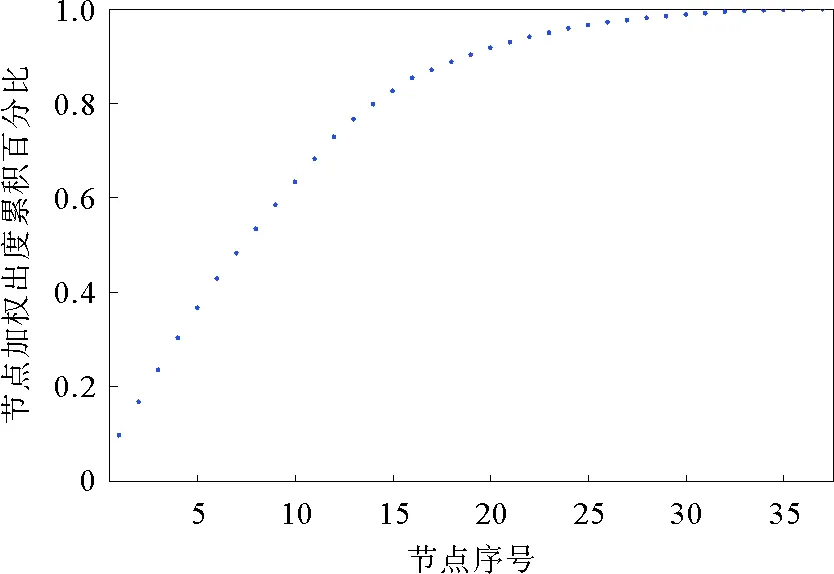
图9 铜铝期货价格波动相关网络节点加权出度累积分布

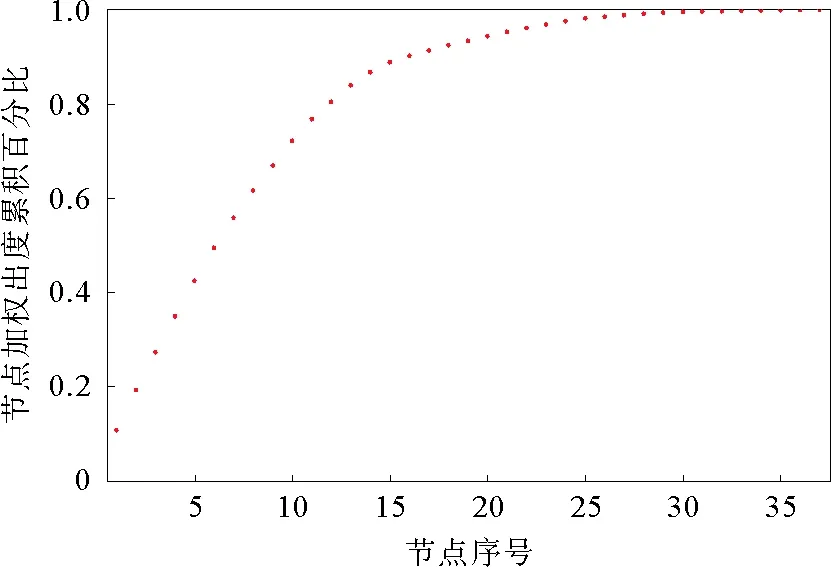
图10 铝锌期货价格波动相关网络节点加权出度累积分布

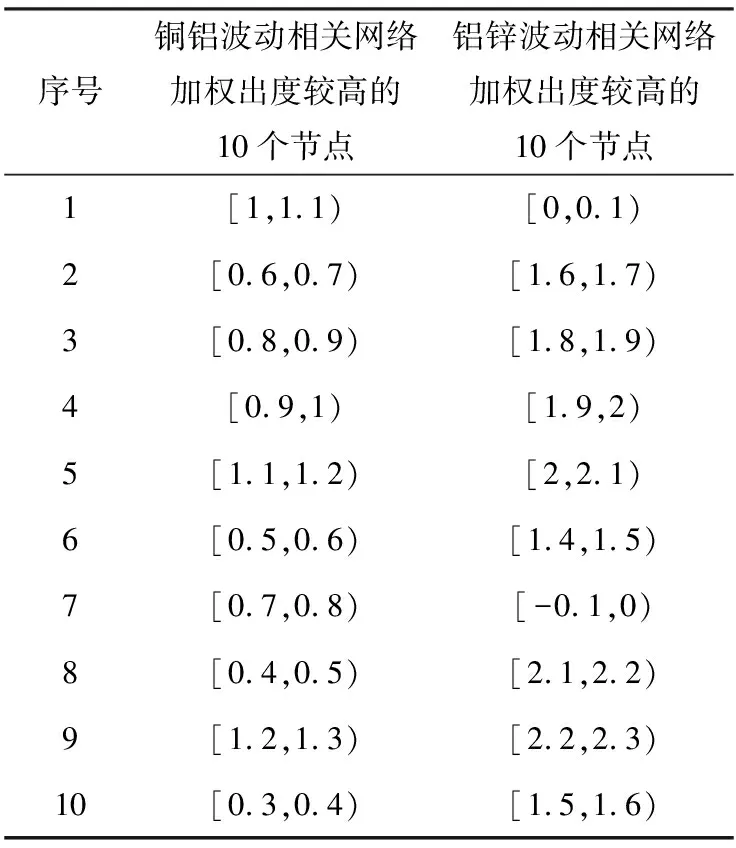
表3 加权出度较高的节点

图9中加权出度较高的10个节点，占总节点数的27.03%，而加权出度累积百分比占总加权出度的63.30%，可以称其为关键节点，如表3所示。这说明对于铜铝波动相关网络的关系模式中较常出现的是这10种模式。图10中加权出度较高的10个节点，占总节点数的25.64%，加权出度累积百分比占总加权出度的66.84%，可以称之为关键节点，如表3所示。这说明铝锌波动相关网络的关系模式中较常出现的是这10种模式。通过对比发现，铝锌期货价格波动相关网络中的关键节点虽然占比不高，但出现的频率相对于铝锌期货价格波动相关网络更高。

加权出度越高，说明该节点在网络中的重要程度越高。除了网络中的第一个和最后一个节点，其他节点的加权出度和加权入度是相等的。由于网络中的节点即铜铝、铝锌期货价格波动相关的一种关系模式，因此，加权出度高，说明该关系模式出现的几率很大，且该关系模式存在较大向其他关系模式转换的可能。该关系模式的出现，表明关系模式极有可能近期发生变化。

3.2 边权分布分析

在铜铝、铝锌期货价格波动相关网络中，模态转换关系表现为复杂网络中的连边，根据边的权重可以确定该类模式转换发生的次数，从边权分布情况可以确定最常发生的关键模式转换类型。

铜铝期货价格波动相关网络中共有143条连边，而铝锌期货价格波动相关网络中有123条连边，将所有的连边按照边权从大到小的顺序排序，设aij表示任意节点i到任意节点j的边权，计算每一条边的边权占所有连边边权之和的比重p(aij)。

(6)

结果表明，在众多连边中，出现了源节点和目标节点相同的情况，我们把其定义为节点的自我转换。铜铝期货价格波动相关网络中自我转换的边有35条，共占比24.48%，而边的权重占比73.98%，这说明关系模式具有很高的稳定性。而铝锌期货价格波动相关网络中自我转换的边有32条，占比26.02%，而边权占比79.08%。从自我转换的连边的情况来看，两个网络区别并不大。边权越高说明该关系模式转换越经常发生，也意味着一种期现货价格关系模式总是倾向于转向某一种关系模式，因此，边权较高的关系模式转换往往意味着较为常见和稳定发生的价格关系转换。

在两个网络中边权占比较高的前10种关键转换模式全部为自我转换，而边权占比的情况有一定差别，铜铝波动相关网络的前10种关键转换模式的边权占比49.22%，而铝锌波动相关网络中该数值为58.65%。这说明两个网络的关键模态都十分稳定，一旦出现以上关键模式，一般会持续一段时间。可以得出大部分时期铜和铝、铝和锌价格波动关系会保持较长时间的稳定而不会轻易改变的结论。同时，还可以发现两个网络相比较，铝锌的价格波动关系更为稳定。

3.3 中介中心度

在铜铝、铝锌期货价格波动相关网络中，中介中心度代表某个关系模式作为关系模式转换媒介出现的次数，即对铜铝、铝锌价格波动相关性关系模式转换的推动能力。节点中介中心度高，则证明该关系模式对铜铝、铝锌价格波动相关性关系模式转换的推动能力越强，我们可以将其称为媒介能力更强。而拥有较强媒介能力的节点的出现可能是市场发生变动的信号。因此，中介中心度较高的节点拥有更强的媒介能力，在网络演化中起着重要的推动作用。

在铜铝期货价格波动相关网络中，节点[-0.1,0)、[-0.3,-0.2)、[-0.5,-0.4)、[1.6,1.7)、[0.7,0.8)有较高的中介中心性，我们可以将其称为关键媒介节点，此类节点推动着铜铝价格波动相关网络的演化。而关键媒介节点所代表的关系模式的出现，往往意味着铜铝期货价格波动相关关系模式拥有更高的转换可能，铜、铝价格波动处于明显的趋势中。而在铝锌期货价格波动相关网络中，关键媒介节点有[0,0.1)、[1.6,1.7)、[1.8,1.9)、[1.9,2)、[2,2.1)。经过对比发现，铜铝价格波动相关网络中的关键媒介模态大部分为铜价和铝价处于反向关系，而铝锌价格波动相关网络则没有出现这一特征。

如图11所示，色带上各种彩色色条代表5个关键媒介节点的出现，铜铝相关网络用蓝色色带表示，铝锌相关网络用红色色带表示。颜色越深，该节点的中介中心度越高。铜铝相关网络的关键媒介节点出现较为分散，而铝锌相关网络的关键媒介节点出现较为集中。从图11还可以看出，两个网络上的关键媒介节点同时集中出现的一段时间铜、铝、锌的价格波动状态往往有较大差异。如左边第一个框中，铜的期货价格急速下跌，但铝和锌的期货价格下跌并不明显。第二个框中，铜的期货价格出现较大波动，但铝和锌则比较平稳。第三个框中，三者均处于平盘趋势，但铜则出现了更为明显的波动。在第四个框中，与第三个框相同，铜价的波动剧烈程度与另外两种有色金属相比更加明显。铜期货价格波动幅度明显大于另外两种有色金属。另外，通过分析图11还可以发现，关键媒介节点集中出现还可以作为3种有色金属关系模式发生较大转变的信号，而且往往也预示着价格趋势在近期会发生变化，可以作为价格预警的一种信号。而下跌趋势中，铜价的变化幅度往往高于铝和锌，因此当市场下行趋势中，铝和锌有更小的风险。

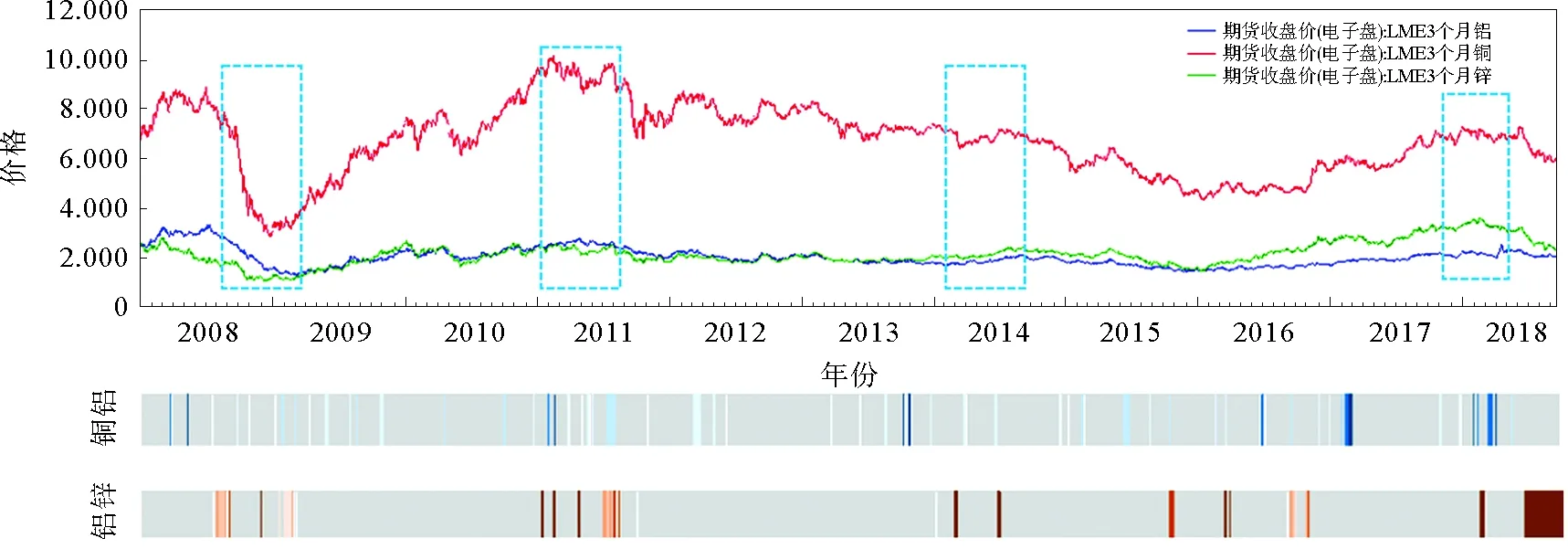
图11 铜铝锌价格波动相关网络关键媒介节点出现时间

3.4 接近中心度

接近中心度较高的节点，即距离其他节点都较近的节点，即其他节点向此类节点的转换历时较短。选取5个接近中心度较高的节点，在铜铝波动相关网络中选取节点[2.4,2.5)、[1.2,1.3)、[1.3,1.4)、[2.3,2.4)、[1.6,1.7)，在铝锌波动相关网络中选取节点[1.5,1.6)、[1.6,1.7)、[1.4,1.5)、[1.2,1.3)、[1.3,1.4)。在图12中，蓝色色带上的色条代表铜铝波动相关网络接近中心度高的5个节点的出现，而红色色带上的色条代表铝锌波动相关网络接近中心度较高的5个节点的出现。无论是蓝色色带还是红色色带，颜色越深，代表节点接近中心度越高。同时，这也表明在网络演化过程中，各个关系模式有较高的可能性转向这几种关系模式。

图12中的虚线框表示两个网络接近中心度较高的节点的同时出现。除了左边第一个和第三个框，其余虚线框所表示的接近中心度较频繁出现的时间，从短期看铜、铝和锌期货价格的波动情况差异不大且市场趋势并不明显，处于横盘状态。因此，在横盘趋势中，铜、铝、锌波动幅度相似，这也意味着期货品种组合投资对控制风险的意义相对于市场上行或下行时要小一些。

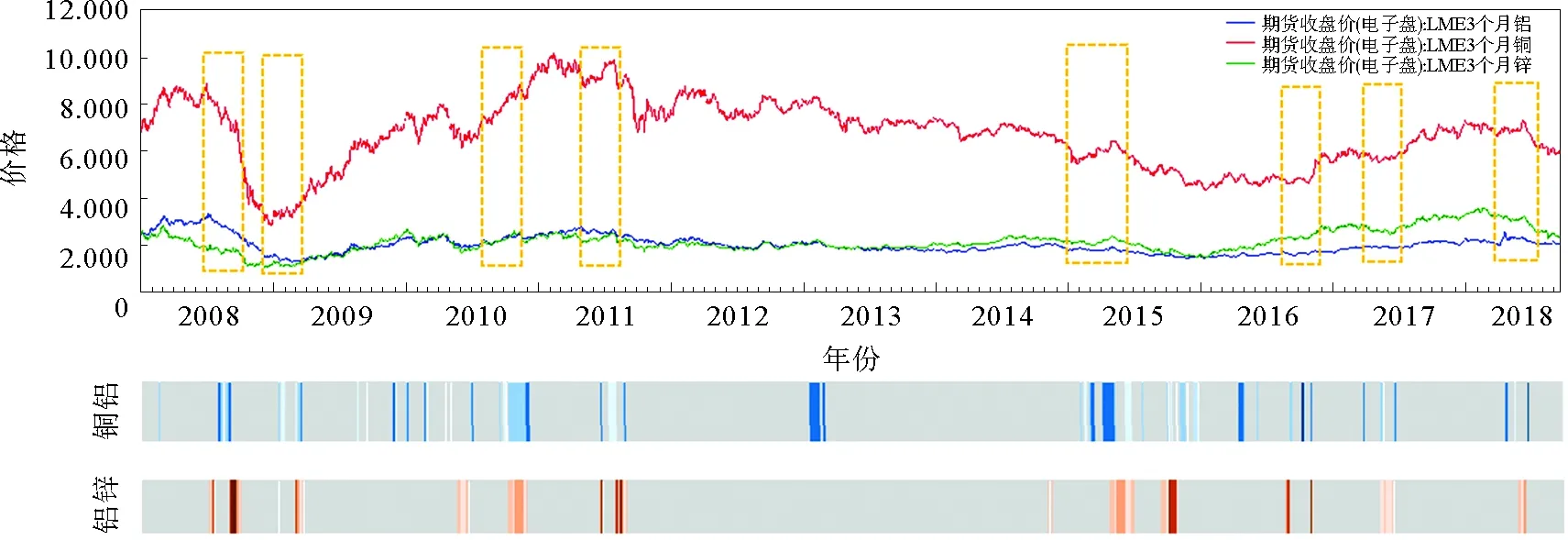
图12 铜铝锌价格波动相关网络接近中心度较高节点出现时间

4 结论

本文基于铜、铝、锌期货价格数据，通过分别对铜和铝、铝和锌价格时间序列进行回归分析，构建了两个基于时间序列的波动相关关系复杂网络，并通过研究其网络拓扑结构发现了其联动效应的潜在规律。通过研究发现，铜和铝价格波动相关关系模式的转换更为活跃，两个网络中均有10种关键关系模式经常出现且存在较大转向其他关系模式的可能，通过对边权分布的分析发现两个网络的关键模式都十分稳定，而通过分析发现中介中心度较高的节点出现可能意味着价格趋势的转变，而3种有色金属价格波动相关关系模式也将发生较大变化。

以往的研究更加注重时间序列之间整体的关联，但对于较长时期的时间序列的关系的研究，尤其在瞬息万变的期货市场，其现实意义将大打折扣。而本文提出了利用复杂网络方法分析时间序列之间短期随时间演化的关系模式的动力学特征，从短期来分析时间序列之间的波动状态及波动状态的演化规律，这对于从细节理解铜铝锌期货价格波动联动效应有很大现实意义。

两个网络中各个节点的α值和β值的变动能够反映一段时间内铜铝锌期货价格联动关系的变化情况，因此不同节点即不同模式之间的连边表明不同模式的转换关系，也意味着联动关系的变化。因此，拥有不同α值和β值的节点之间的连边是联动关系变化的标志，应该尤其注意。

运用节点中介中心度分析可以帮助投资者识别联动关系变化的时间点，提高价格预警的准确性，投资者可以根据关键媒介节点的集中出现帮助更有效识别价格趋势转变的信号，从而帮助规避市场风险，实现套期保值，降低采购成本，提高利润率。

接近中心度较高节点的出现可以帮助识别铜铝锌价格联动趋势与市场趋势。接近中心度较高节点频繁出现的时间段往往是市场处于横盘且铜、铝、锌价格波动幅度与状态相似的阶段，期货组合投资对降低风险的意义会稍微有所降低。

由于节点自我转换的边权占比较高，α值和β值保持不变的关键模式转换也占有较大比例，因此铜铝锌价格联动关系模式倾向于保持较长时期的稳定，可以较准确预测出铜铝锌价格联动关系的关系模式。对于投资者来说，这将给其套利带来帮助。

本文将铜、铝、锌3个时间序列中的铜和铝和、铝和锌分别进行回归分析构建了复杂网络，并通过分析其网络结构分析了其关系模式的演化规律，这种方法的应用可以扩展至多个领域，如股票市场、国际贸易等。但是，时间和篇幅所限，本方法只是对3个时间序列进行了分析，虽然可以帮助理解价格趋势，但模型中没有考虑现实中的其他因素，如产业链状况、供求情况等。进一步研究的方向将是将现实中的其他影响因素在建模中予以考虑。