几种堆石料双曲线模型参数整理方法的比较

侯伟亚，张兆省，张幸幸，皇甫泽华，邓 刚，温彦锋

(1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100048；2.河南省前坪水库建设管理局，河南 郑州 450003)

0 引 言

双曲线模型是土石坝应力变形分析中应用较广的一类本构模型。1963年，康德等[1]提出用双曲线拟合土体常规三轴试验中偏差应力和轴向应变的关系，即

(1)

式中，a、b为试验常数；(σ1-σ3)为偏差应力；εa为轴向应变。

邓肯等[2-3]在此双曲线关系的基础上提出了目前广泛应用的邓肯-张E-v及邓肯E-B增量弹性模型。沈珠江等[4]建议的双屈服面模型中，仍建议用双曲线来拟合常规三轴试验条件下的(σ1-σ3)～εa关系。高莲士等[5]建议在非线性解耦K-G模型中，假定常规三轴剪切试验中应力比与剪应变之间存在双曲线关系。以上几种本构模型可统称为双曲线模型。双曲线模型的显著优点是参数可以通过常规三轴试验测定，物理意义明确，易于接受，因而在国内外土石坝的静力变形分析中得到广泛采用[6]。

合理确定本构模型参数对土石坝应力变形分析结果的合理性有着至关重要的影响[7]，许多研究[8-11]都围绕合理确定土石坝筑坝材料的本构模型参数展开。在土石坝工程实践中，常用的双曲线模型参数a、b的整理方法主要有两种：一种是直线拟合法，将纵坐标轴变换为εa/(σ1-σ3)，对εa/(σ1-σ3)～εa的试验点据进行直线拟合，可得b为直线的斜率，a为直线的截距；另一种是邓肯等[2]提出的两点法，在εa/(σ1-σ3)～εa坐标系中，过偏差应力为70%和95%抗剪强度的数据点做直线，该直线的截距、斜率分别为a、b。SL237—1999《土工试验规程》[12]中建议用后一种方法来推求邓肯E-B模型的参数；DLT 5355—2006《水电水利工程土工试验规程》[13]则未对上述两种方法做倾向性规定。在实践中，对于同一种土石坝筑坝材料，这两种方法求得的双曲线模型参数通常是不同的；国内一些研究者对两种方法进行了比较，对于不同类型的土往往得出不同的结论[14-15]。还有一些研究者提出了新的参数整理方法，如朱俊高等[8]、陈力宏等[16]建议对一组三轴试验结果进行反演，这一方法实际应用难度较高，由于反演策略的不同有时难以求得唯一解，同时，反演得到的参数只代表数值上的最优解，并不一定符合其物理意义[17-18]；刘大康等[19]认为，堆石坝工程中堆石体的实际应变是比较小的，在整理参数时应该更加注重对小应变数据点的拟合，提出将邓肯的两点法中，过偏差应力为70%和95%抗剪强度对应的数据点，改为过偏差应力为50%和70%抗剪强度对应的数据点来做直线。

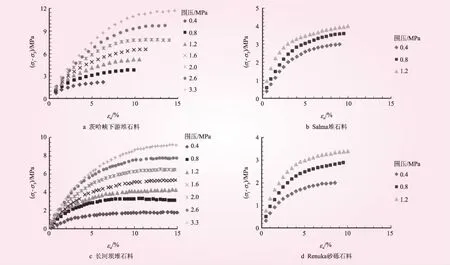
图1 典型堆石料的三轴试验结果

笔者认为，直线拟合法或两点法是限于过去的计算条件、从简便的角度出发提出的，在计算机技术已经非常发达的今天，完全可以采用曲线拟合法，借助有关软件直接对试验点据进行曲线拟合来获取双曲线模型参数的最优解，该方法更为便捷。

本文以邓肯模型为例，采用4种方法(直线拟合法，邓肯等建议的两点法，刘大康等建议的两点法，曲线拟合法)分别整理几种典型堆石料的邓肯-张模型参数K、n、Rf，并比较采用不同参数整理方法时模型预测结果与试验结果的误差。在此基础上，探讨不同双曲线模型参数整理方法优缺点和适应性。

1 分析过程简述

1.1 典型堆石料的试验曲线和强度参数

本文对文献[19-21]中4座典型土石坝工程中坝壳料的典型试验结果(如图1所示)进行分析，其中茨哈峡、Salma和长河坝均为爆破堆石料的试验结果，Renuka坝为砂砾石料的试验结果。

堆石料和砂砾石料的抗剪强度均可用Leps等[22]建议的公式进行描述，即

φ=φ0-Δφ(σ3/pa)

(2)

式中，φ为围压为σ3时的内摩擦角；pa为标准大气压；σ3为围压；φ0和Δφ为非线性强度指标。

4种堆石料的强度指标列于表1。已知强度指标，则可以求得任意围压下σ3的抗剪强度。即

(3)

式中,(σ1-σ3)f、σ3为围压；φ为围压为σ3时的内摩擦角。

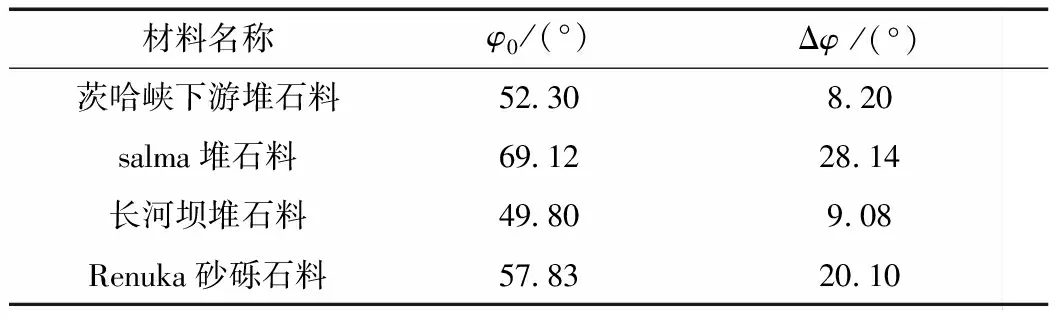
表1 4种堆石料的强度指标

1.2 模型参数的确定

对图1所示的4组试验数据分别通过下述4种方法来整理试验常数a、b。

(1)直线拟合法。将所有试验数据点绘在εa/(σ1-σ3)～εa坐标系中，通过Excel软件进行直线拟合，通过Slope函数求取斜率b，通过Intercept函数求取截距a。

(2)邓肯的两点法。在试验数据系列中，选取偏差应力最接近70%(σ1-σ3)f和95%(σ1-σ3)f的两个试验点据，过这两点做直线，直线的截距为a，斜率为b。

(3)刘大康的两点法。在试验数据系列中，选取偏差应力最接近50%(σ1-σ3)f和70%(σ1-σ3)f的两个试验点据，过这两点做直线，直线的截距为a，斜率为b。

(4)曲线拟合法。在(σ1-σ3)～εa坐标系中，通过Origin软件进行双曲线的曲线拟合，直接确定参数a、b。

求得不同围压下的试验常数a、b后，根据邓肯等建议，通过式(4)、(5)求取不同围压下的初始剪切模量Ei和应力比Rf。即

Ei=1/a

(4)

Rf=b(σ1-σ3)f

(5)

取各个围压下平均的Rf作为该土料的Rf；将不同围压下的Ei/pa和σ3/pa绘制在双对数坐标中进行直线拟合，可以得到直线的斜率对应参数n，截距对应参数K。至此，可以求得邓肯模型的3个重要参数K、n和Rf。

对于本文提到的4种典型堆石料的试验结果，通过4种不同的方法整理参数a、b，进一步求得邓肯模型的参数K、n和Rf，结果列于表2，可知不同的参数整理方法对求得的参数值有显著影响，对于茨哈峡下游堆石料，不同参数整理方法得到的参数K可相差60%以上，n可相差超过100%，Rf的差异稍小，但也接近20%。

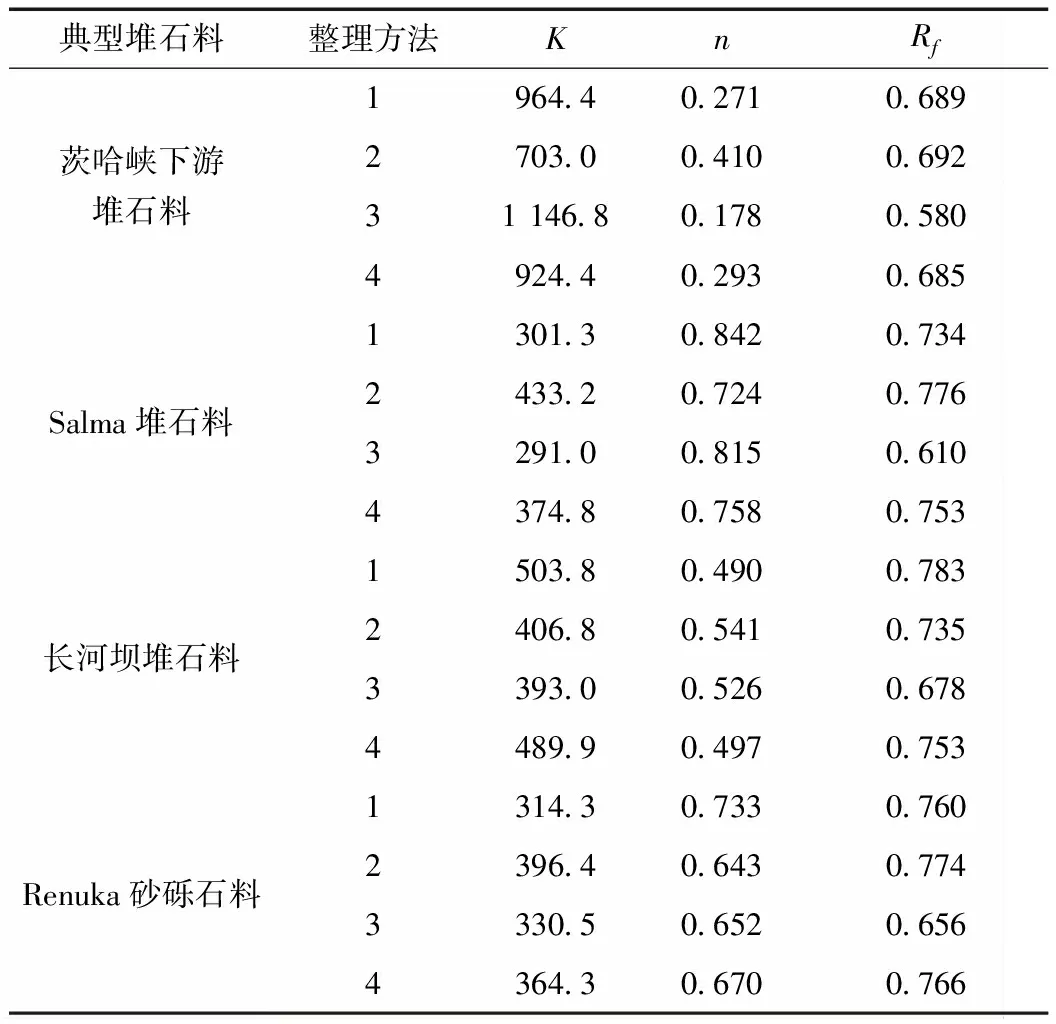
表2 不同方法整理得到的K、n和Rf

1.3 误差分析

求得邓肯模型参数K、n和Rf，可以推算任意围压σ3下堆石料的偏差应力-轴向应变关系曲线，即

(6)

一般情况下，模型表现与试验不可能完全一致，式(6)推算的曲线与试验曲线不可避免的存在一定的偏差。图2给出了采用不同参数整理方法时，茨哈峡下游堆石料试验点据与计算应力应变曲线的对比情况。

为了评价模型推求结果与试验结果之间偏差，定义如下的误差函数

(7)

为了便于分析，将表2所列几种堆石料不同方法求取参数对应的误差函数F以折线图的形式绘制在图3和图4中。由于Renuka砂砾石料的误差函数整体上比堆石料要小一个数量级左右，为了便于观察，将Renuka砂砾石料和其他3种堆石料分开绘制。图3是考虑所有试验点据的条件下，模型推求结果与试验结果之间的误差函数值。大量的计算分析结果表明，堆石坝坝壳的压缩应变很少超过5%，因此图4绘制了只考虑轴向应变小于5%的试验点据时的误差函数F。

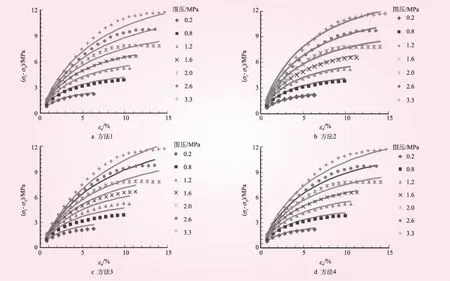
图2 茨哈峡下游堆石料试验和计算应力-应变关系对比

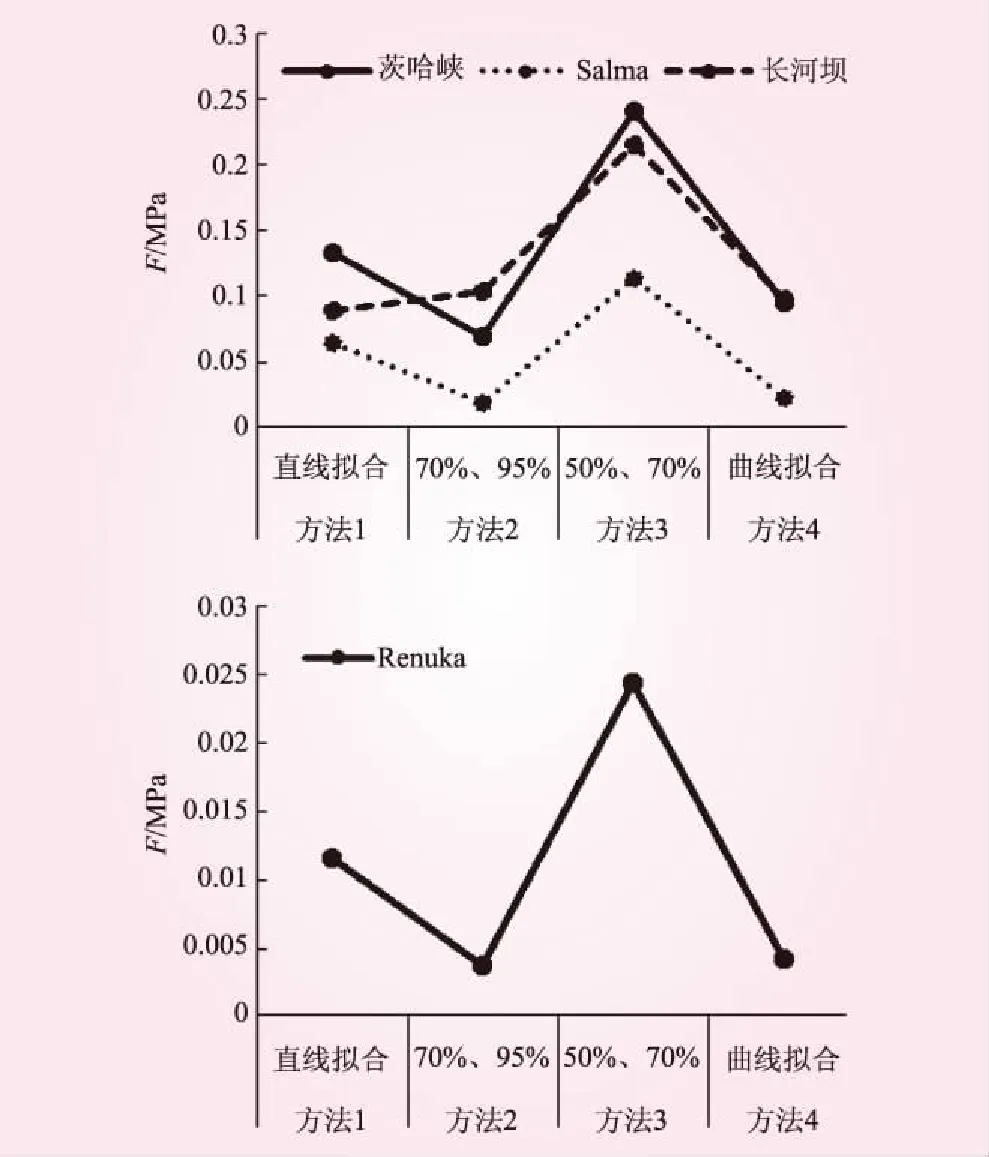
图3 误差函数F与参数整理方法的关系(所有试验点据)

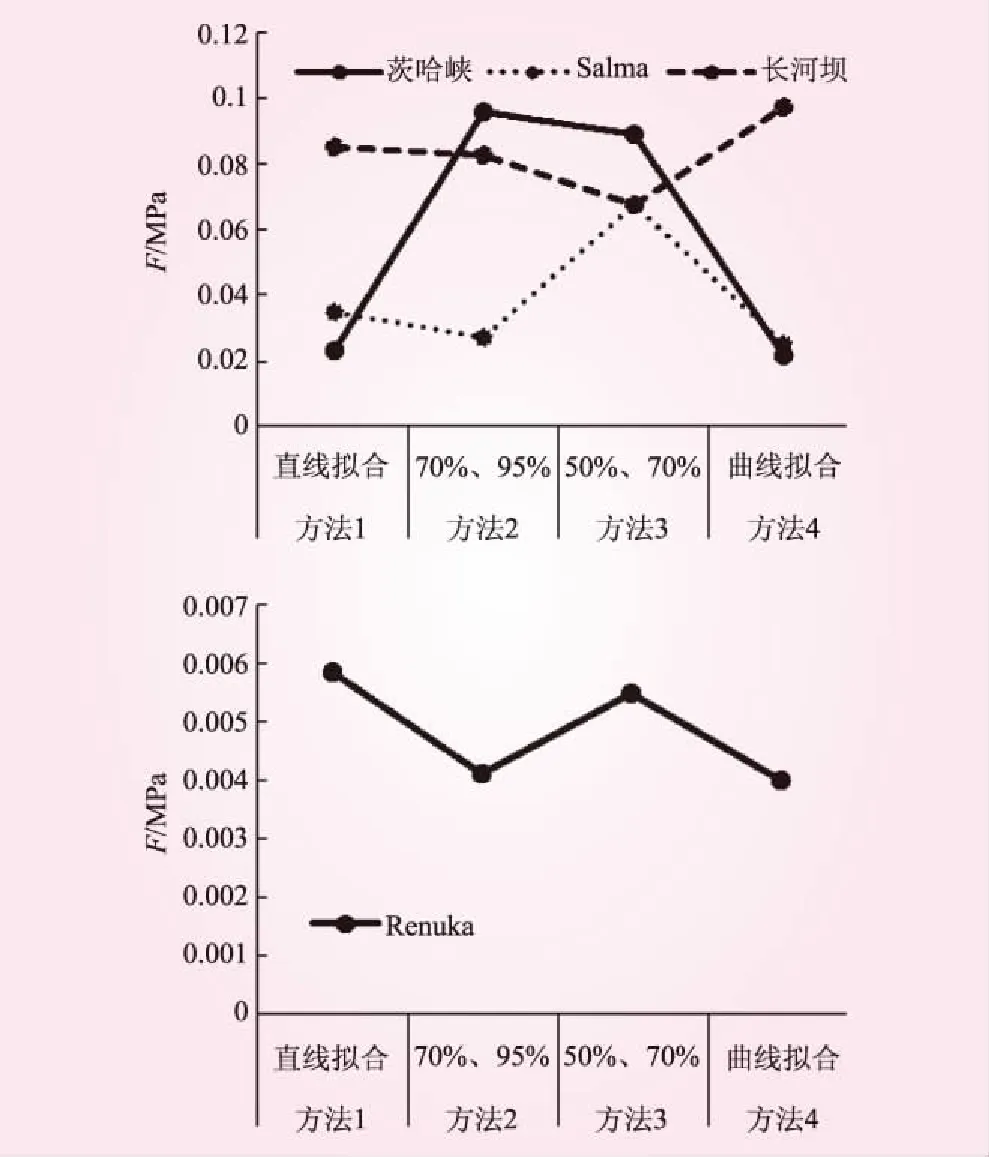
图4 误差函数F与参数整理方法的关系(应变小于5%时)

从图3可以看到，4种材料采用曲线拟合法及邓肯的两点法推求参数的误差函数值F最小；采用刘大康的两点法推求参数的误差函数值F最大。从图4可知，仅考虑轴向应变小于5%的试验点数据时，对不同材料，参数整理方法对误差的影响规律不甚一致。对茨哈峡，邓肯的两点法和刘大康的两点法求得参数的误差函数值F明显大于直线拟合法和曲线拟合法，对Renuka砂砾石料，采用直线拟合法和刘大康的两点法整理参数的误差稍大。综合来看，采用曲线拟合法整理参数的误差较小。

2 讨 论

2.1 模型预测与试验数据之间误差的来源

本文中误差函数F表征了模型预测曲线与试验点据之间的偏差，这与一般曲线拟合误差的含义不同，实际上包含了两个层面的误差。一是整理试验常数a、b的过程产生的误差，由于曲线拟合本身就是求使得单条曲线误差函数F最小的参数，从理论上即可直接推断“曲线拟合法”的误差最小；二是通过a、b求邓肯模型参数K、n和Rf的过程产生的误差。一般而言，不同围压下求得的Rf并不一致，只能取平均值作为材料的Rf，lg(Ei/pa)和lg(σ3/pa)通常也并不严格地符合直线关系，只能通过直线拟合求得K和n，这一过程会产生新的误差。图5以茨哈峡下游堆石料为例，反映了这一现象。理论上，第二个层面的误差与参数整理方法没有直接联系。在整理本文所述几种堆石料的参数时发现，对于茨哈峡下游堆石料，采用两点法整理参数时，不同围压下确定的Rf差异较大，lg(Ei/pa)和lg(σ3/pa)的关系偏离直线关系也较明显(如图5和图6所示)；对于其他3种堆石料，4种整理方法在第二个层面的误差上没有显著差别。

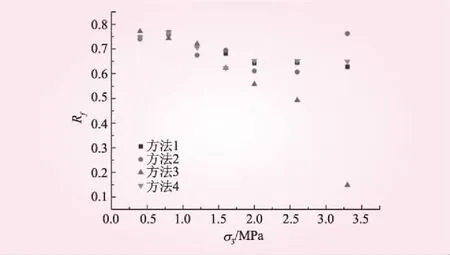
图5 茨哈峡下游堆石料Rf与 σ3和参数整理方法的关系

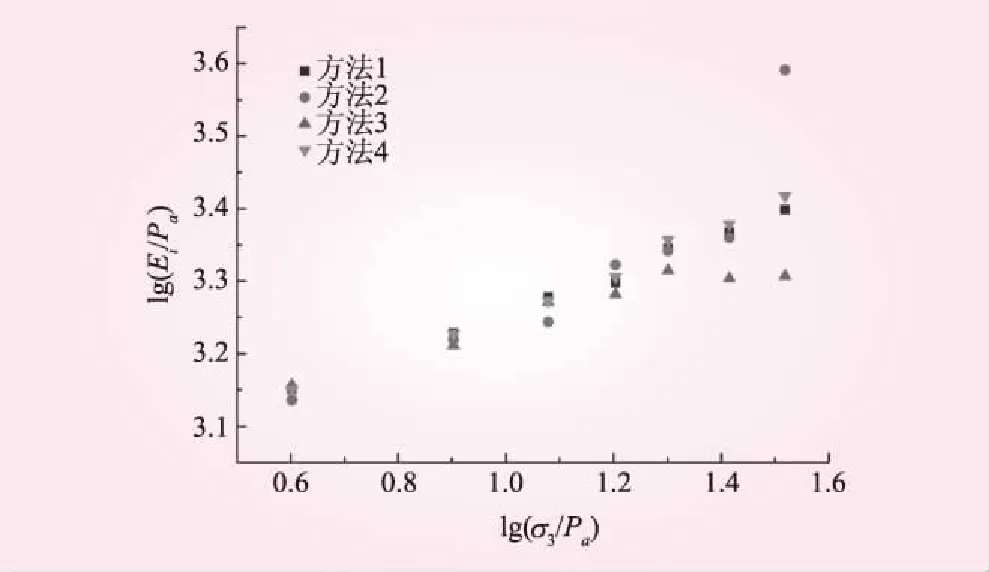
图6 茨哈峡下游堆石料lg(Ei/pa)与lg(σ3/pa)和参数整理方法的关系

2.2 直线拟合法和两点法的对比

在求取堆石料双曲线模型参数的实践中，小应变条件下εa/(σ1-σ3)～εa点据偏离直线段，是一种比较常见的现象，此时，如果对所有的数据点进行直线拟合，则拟合直线受起始段数据点的影响较大，偏离试验曲线的直线段。因此，邓肯等建议采用偏差应力为70%(σ1-σ3)f和95%(σ1-σ3)f的两个试验点据的连线来代替拟合直线，该方法能较好的回避试验曲线起始段偏离直线段的问题。一些研究者提出改变这两个点的位置，取偏差应力更小的数据点(如偏差应力为抗剪强度的50%和70%)来做直线，以期提高对小应变条件下应力应变关系的拟合精度。从本文的误差分析结果来看，这种方法收效不佳。图7以Salma堆石料为例做出说明。对于0.4 MPa围压下的试验点据，由于起始段偏差较明显，拟合直线偏离试验曲线的直线段；偏差应力为70%(σ1-σ3)f和95%(σ1-σ3)f的两个试验点据的连线与试验曲线的直线段符合较好；偏差应力为50%(σ1-σ3)f和70%(σ1-σ3)f的两个试验点据恰好跨越试验曲线的拐点，过这两点的直线与试验曲线有较大程度的偏离。

图7 Salma堆石料的参数整理方法对比

2.3 曲线拟合法的优势

对本文讨论的4种堆石料而言，采用邓肯等建议的两点法或者曲线拟合法整理双曲线模型参数，均可使邓肯模型的预测值与试验值的误差较小。但对一些特殊问题，曲线拟合的灵活性更强。

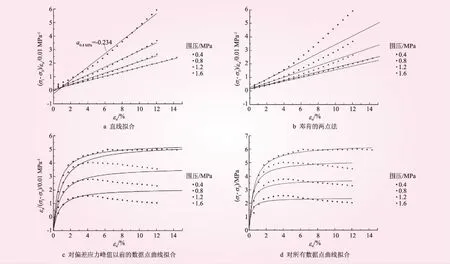
图8 九甸峡垫层料的三轴试验结果和参数整理方法对比

图8给出了一种细堆石料(九甸峡面板堆石坝垫层料)的一组三轴试验结果，在εa/(σ1-σ3)～εa坐标系中部分试验右端上翘的趋势。对于这种情况，如果对所有数据点进行直线拟合，则可能会出现截距(初始模量的倒数)为负的情况；如果仅对偏差应力峰值以前的数据点进行直线拟合或采用两点法，则会出现不同围压下拟合直线截距非常接近(此时n≈0，即材料几乎没有压硬性)、拟合直线偏离大部分试验数据点的情况。无论哪种情况，均与邓肯模型参数的物理意义不甚相符。曲线拟合可以根据需要，仅对峰值以前的数据点拟合(图8c)或者对整条试验曲线进行拟合(图8d)。结合一些研究者的建议，模型参数确定应更注重对小应变下堆石料的应力应变数据的拟合，也可采用曲线拟合法来处理，自定义拟合数据点的范围。

3 结 论

本文对双曲线模型参数整理方法进行了探讨。结合4种典型堆石料的三轴试验结果，比较了采用4种不同的参数整理方法时，模型预测结果与试验结果之间的误差。在此基础上，对不同参数整理方法的优缺点进行了分析，得到主要结论如下：

(1)对于对应力-应变规律与双曲线符合较好的堆石料而言，采用邓肯的两点法或曲线拟合法都可使邓肯模型预测结果与试验结果之间的误差较小；采用直线拟合法或刘大康的两点法时，参数整理结果易受到试验曲线起始段偏离直线关系的影响，导致模型预测结果与试验结果之间的误差较大。

(2)仅从堆石料模型预测和试验结果的误差而言，邓肯的两点法和曲线拟合法都可以较好的控制误差，但曲线拟合方法具有更好的适应性和灵活性，对于一些特殊情况，传统方法受到较大限制时，曲线拟合也可较好地解决问题。