基于Exponentiated Weibull 湍流模型的OFDM光链路性能分析

张 韵,王 翔,赵尚弘,蒙 文,赵 静,刘 韵,丁西峰

(空军工程大学信息与导航学院,陕西 西安 710077)

1 引 言

激光通信由于具有带宽容量大、抗干扰能力强、部署快速简便等优点,被视为突破射频通信限制、提供高速无线通信能力的最佳候选方案之一[1-2]。因此,利用激光链路建立Gbit/s量级的航空通信骨干链路构建空天地一体信息网络,能够充分发挥航空信息网络在信息获取、传输、处理和分发领域的得天独厚优势,成为空间信息领域研究的热点[3-4]。

然而,航空激光通信链路极易受到云、雨、雾等大气效应以及平台振动的影响,导致接收端光强的起伏,严重影响到机载激光通信链路的性能。因此,平台位置不稳定以及大气湍流效应对机载激光通信链路性能的影响成为机载激光通信亟需解决的问题。正交频分复用(OFDM)是一种多载波调制方式,将多个独立的数据流通过频率不同的多个副载波进行调制,具有良好的抗频率选择性衰落,抗窄带干扰及信道利用率高的特性。文献[5]采用Gamma-Gamma大气湍流分布模型,在FSO中引入OFDM方案,分析了M-QAM调制下OFDM链路的平均误码率；文献[6]采用Lognormal分布的弱大气湍流模型,在OOK调制方式下对非对称限幅光OFDM系统误码性能进行了研究；文献[7]基于Gamma-Gamma大气湍流模型,进行实验验证了FSO-OFDM通信系统具有较好的抗码间串扰性能,误码率低于单载波调制系统。上述研究工作只考虑大气湍流效应,没有考虑平台不稳定性对激光通信链路性能的影响。另外,大气湍流模型采用适用范围受限的Lognormal分布模型或者Gamma-Gamma分布模型。2012年,Barrios R和Dios F提出了适用于弱到强湍流及孔径平均条件下的新型Exponentiated Weibull大气湍流模型[8-9]。因此,本文针对航空激光通信特点,基于Exponentiated Weibull 分布大气湍流模型,联合指向误差对采取M-QAM调制方式的OFDM系统性能进行研究。

本文首先给出Exponentiated Weibull 分布大气湍流衰减模型及OFDM链路模型,分别仅考虑大气湍流影响及综合大气湍流和指向误差对误码率的影响,利用MeijierG函数推导出OFDM链路平均误码率的闭合表达式,最后通过闭合表达式进行仿真,分析了不同参数与误码率的关系。

2 OFDM链路模型

OFDM是一种多载波调制传输方式,将高速的数据流划分为并行的低速数据流通过若干窄带副载波进行传输。副载波的调制方式为PSK或QAM,调制后在子信道中进行高频传输。传输中严格选择副载波间距,使副载波之间相互正交。信道之间的相互干扰可忽略,发送端通过快速逆傅里叶变换(IFFT)产生多个相互正交的副载波,接收端无需使用均衡技术通过傅里叶变换(FFT)从正交信号中恢复原信号[10]。

假设OFDM信号包含N个副载波,通过上变换至载波频率fc,公式表达为[5]:

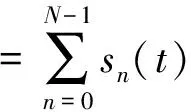
(1)

式中,{wn=2πn/Ts,n=0,1,…,N-1}为一组正交载波频率,Ts为OFDM符号持续时间,Xn=an+ibn为第n个副载波的复数据信号,an和bn分别为同相和正交调制符号, 原始数据依据数据速率通过不同的调制方式(PSK或QAM)进行映射,这里设置保护间隔为0；因此OFDM信号周期Ts与傅里叶分析窗口运行时间一致。由于频率选择性,窄带副载波在不同信道的增益可忽略。

SOFDM(t)信号用来调制LD的光强度,忽略LD的非线性因素,LD的光功率输出P(t)公式表示为[5]:

(2)

式中,Pt为平均发送光功率；mn为第n个子载波的光调制系数(OMI),总的光调制系数mtotal表示为[5]:

(3)

经过大气传播损耗、大气湍流和指向误差的影响,接收端光检测器的接收光功率公式表示为[5]:

Pr(t)=P(t)Lαh+N(t)

(4)

式中,Lα为大气传播损耗,包括了雨及能见度减少等引起的损耗;N(t)为信道噪声功率；大气湍流影响因子ht和指向误差因子hp两部分组成信道衰减因子h,即:

h=hthp

(5)

信道噪声经过光电检测器滤波后被滤除,接收端处光电检测器输出光电流i(t,h)表示为:

(6)

式中，I0=ρLαhPt;ρ为光电检测器的响应度；n0(t)是探测器引入的噪声,包含热噪声、 散粒噪声、相对强度噪声RIN,总的噪声功率定义如下[3]:

(7)

式中,Tabs为噪声热力学温度;KB为玻尔兹曼常量;RL为PD的负载阻抗;q为单位电子的电荷量。

为简化运算假设所有副载波的调制系数相同[5]:

(8)

副载波在频率为wn的信号功率为[3]:

(9)

接收端每一个副载波的载波噪声比(CNRn)定义为信号光功率C与噪声功率N0/Ts的比值[5]:

(10)

3 链路性能

OFDM信号包含N个副载波,采用M-QAM调制方式。每个副载波误码率表示为Pe,n,公式表示为[5,11-13]:

(11)

其中,A=3/2(M-1);erfc(·)为误差补函数。

当副载波数量很大时,OFDM链路的总平均误码率为[5,11-13]:

(12)

式中,M为调制阶数;M=2k,k是偶数;erfc(·)为误差补函数。

根据信道衰减因子h的联合概率密度函数,OFDM链路总平均误码率Pe,av可计算为[5,11-13]:

(13)

将式(13)中的erfc(·)用Meijer G函数[14]表示为:

(14)

3.1 仅大气湍流作用下平均误码率

现有的激光链路的大气湍流模型大多基于Lognormal分布模型和Gamma-gamma分布模型。但上述两种模型的适用范围不同,Lognormal模型适用于弱湍流条件下,Gamma-Gamma模型适用于中强湍流条件下。2012年,Barrios R和Dios F提出了全新的适用于弱到强湍流及孔径平均下的Exponentiated Weibull分布模型,故本文采用Exponentiated Weibull分布模型[8]：

(15)

其中,α>0,β>0；η为与光强有关的参数,且η>0,通过曲线拟合的方法得到经验公式:

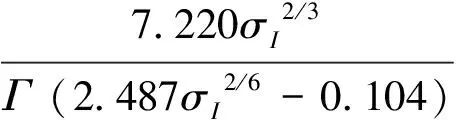
(16)

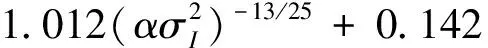
(17)

(18)

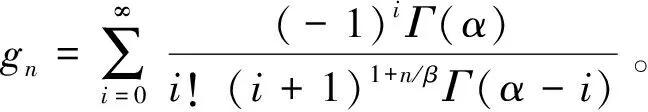
仅考虑大气湍流对误码率的影响,将式(10)、(15)代入式(13),利用Meijer G函数的性质[14],可推导出总平均误码率Pe,av闭合表达式为:

(19)

式中,Δ(K,A)=A/K,A+1/K,…,A+K-1/K,l和k为满足l/k=β/2的整数。

3.2 大气湍流与指向误差联合作用下平均误码率

系统中大气湍流与链路指向误差共同影响接收光信号的强度,由指向误差理论得光链路指向误差因子hp的概率密度函数可表示为[15]:

(20)

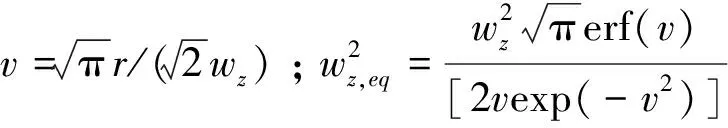
信道衰减因子h=hthp的联合概率密度函数可计算为[15]:

(21)

利用Meijer G函数的性质[11]推导得信道衰减因子h的联合概率密度函数的闭合表达式为:

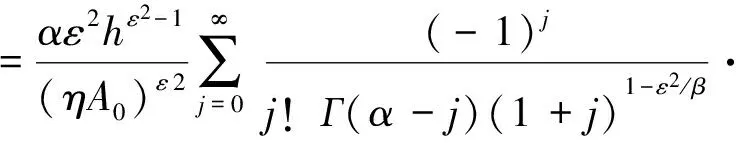
(22)

综合考虑大气湍流及指向误差对误码率的影响,将式(10)、(22)代入式(13),利用Meijer G函数的性质[14],可推导出总平均误码率Pe闭合表达式为:

(23)

式中,Δ(K,A)=A/K,A+1/K,…，A+K-1/K,l和k为满足l/k=β/2的整数。

4 仿真结果分析

为了研究不同参数对系统平均误码率的影响,根据推导的闭合表达式(22)和(23)进行仿真分析。表1为系统设置参数。文中取OFDM信号副载波数N=1000,每一副载波调制系数均为mn=0.002。

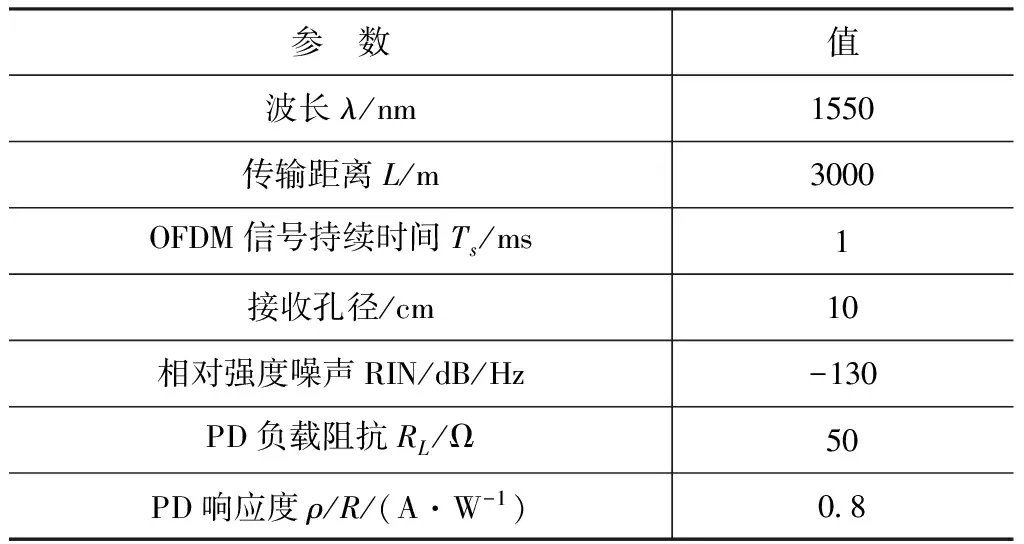
表1 仿真参数

4.1 仅大气湍流下平均误码率仿真分析

图1为M=4,即副载波采用4-MQAM调制方式,不同大气湍流强度下,误码率随发射功率的变化关系。由图可知,同一湍流强度下,发射功率增大,误码率降低；同一发射功率下,湍流强度增大,误码率增加。在中,弱湍流下,误码率随发射功率的增加有显著的改善,而在强湍流条件下,随着发射功率的增加,误码率改善缓慢。在相同误码率要求下,弱湍流所需发射功率最小。

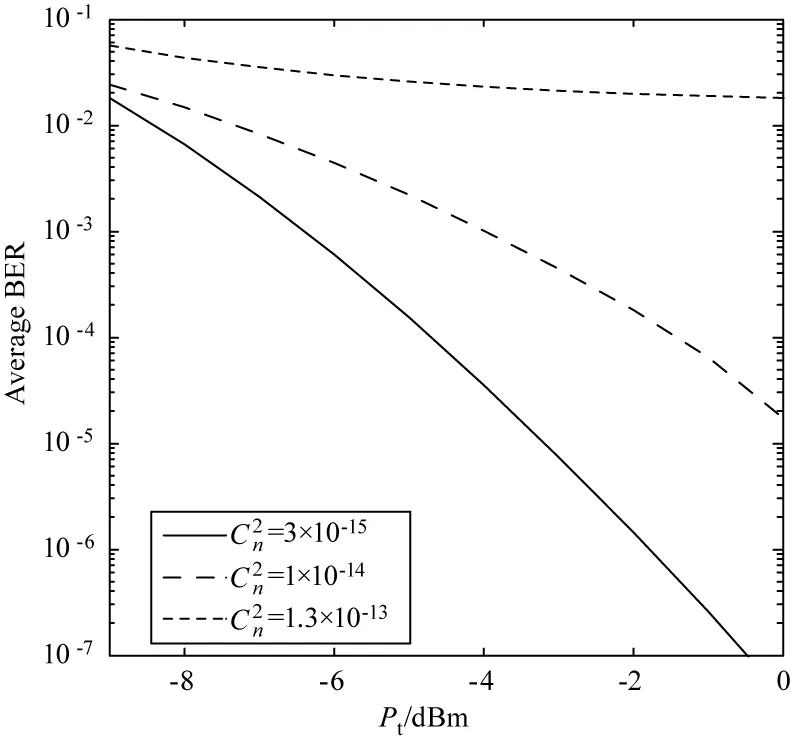
图1 M=4,不同大气湍流强度下,误码率随发射功率变化关系

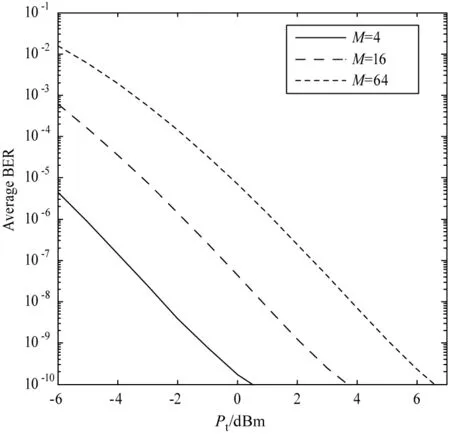
图2 当Cn2=1×10-14时,不同调制阶数下误码率与发射功率的关系

4.2 大气湍流联合指向误差影响下平均误码率仿真

图3为M=4,即副载波采用4-MQAM调制方式,σs/r=0.5,wz/r=1时,不同大气湍流强度下,误码率随发射功率的变化关系。由图可知,在弱湍流时,Pt=-9 dBm,Pe=3.091×10-2；Pt=-4 dBm,Pe=1.732×10-4；Pt=1 dBm,Pe=6.251×10-6。可知发射功率每增加5 dBm,误码率降低了两个数量级。在中湍流时,Pt=-9 dBm,Pe=9.86×10-3；Pt=-4 dBm,Pe=7.469×10-4；Pt=1 dBm,Pe=2.868×10-5。可知发射功率每增加5 dBm,误码率降低一个数量级。同一发射功率,湍流越小,系统性能越好。同时与图1相比,图3中要达到与图1相同的误码率,所需的发射功率增加,这说明了指向误差对系统性能造成了不利影响。

图4仿真了中湍流强度Cn2=1×10-14,σs/r=0.5,wz/r=1,时,不同调制阶数M=4,16,64下,误码率随发射功率的变化关系。图4与图2类似,同一调制阶数下,误码率随着发射功率的增加而降低；同一发射功率下,误码率随着调制阶数的减小而降低,副载波采用不同调制阶数进行调制时,发射功率对链路误码率影响程度近似。M=16时,Pt=-9 dBm,Pe=9.86×10-3；Pt=-4 dBm,Pe=7.469×10-4；Pt=1 dBm,Pe=2.868×10-5。发射功率每增加5 dBm,误码率降低1个量级,与未加指向误差的图2中发射功率每增加5 dBm,误码率降低4个量级相比,发射功率的增加对误码率对误码率改善的程度较低。

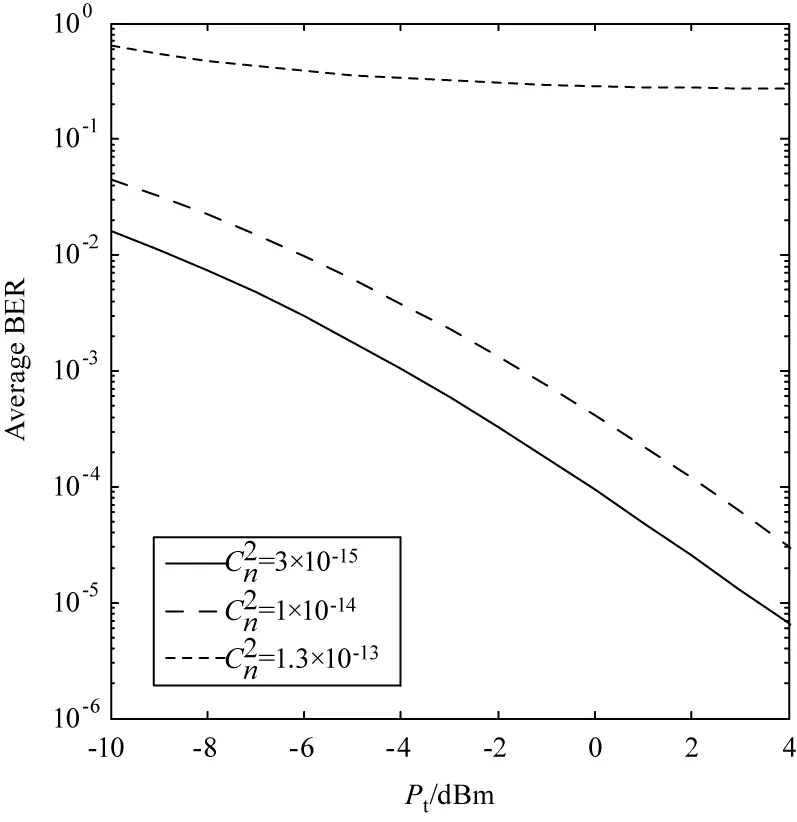
图3 当M=4,σs/r=0.5,wz/r=1时,不同湍流强度下的平均误码率与发射功率的关系

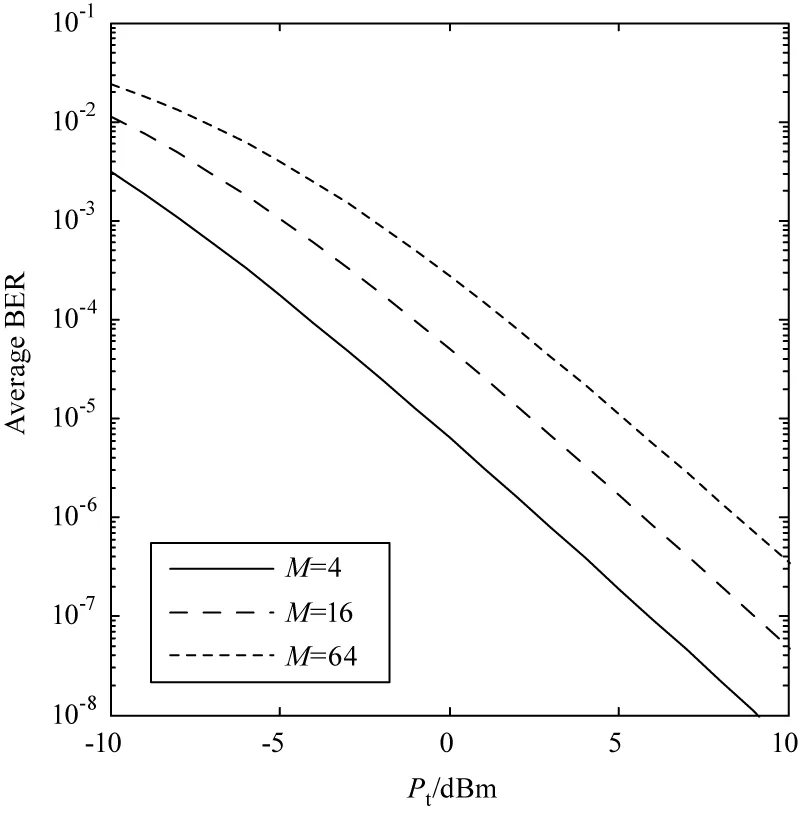
图4 当Cn2=1×10-14,σs/r=0.5,wz/r=1时,副载波不同

图5为在中湍流强度Cn2=1×10-14,调制阶数M=4,接收端处波束宽度与接收机半径比值为wz/r=1时,在不同接收端处抖动标准差与接收机半径的比值σs/r条件下,OFDM链路平均误码率与发射功率的关系。从图中可以看出,随着接收端处抖动标准差与接收机半径的比值σs/r增大误码率增大,这是由于σs/r的增大表明指向误差对链路的影响越强,故误码率越大。在Pt=0 dBm的条件下,当σs/r=0.5时,链路的平均误码率为6.385×10-6,当σs/r=0.7,Pe=1.020×10-3增加了三个量级,当σs/r=1,Pe=1.989×10-2,增加了一个量级。所以采取一定的措施减少指向误差对链路的影响,可提高系统的通信性能。由图可知,同一σs/r值下,误码率随着发射功率的增大而减小。当σs/r=0.5时增大发射功率对降低链路平均误码率较为明显,发射功率每增加5 dBm,误码率降低1.5个量级。

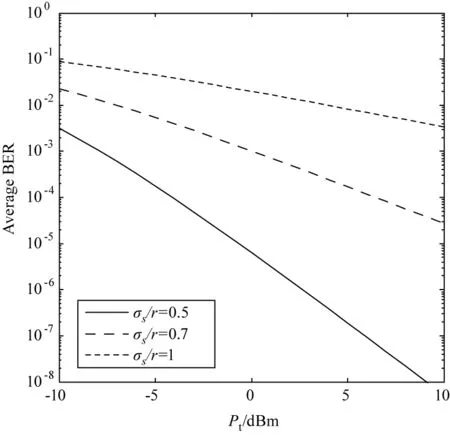
图5 当Cn2=1×10-14,M=4,wz/r=1时,不同σ/r比值下的平均误码率与发射功率的关系

图6为在中湍流强度Cn2=1×10-14,调制阶数M=4,σs/r=0.5条件下,不同接收端处波束宽度与接收机比值wz/r时OFDM链路平均误码率与发射功率的关系。由图可知,随着wz/r增大即几何传播损耗增大,链路误码率增加。增大发射功率可以补偿几何传播损耗对链路性能造成的影响,降低链路平均误码率。当Pt>-4 dBm时,wz/r=1,wz/r=1.5条件下功率增大对误码率的影响效果近似相同。wz/r=0.5时,发射功率增加对误码率改善效果显著,发射功率每增加5 dBm,误码率性能改善两个量级。

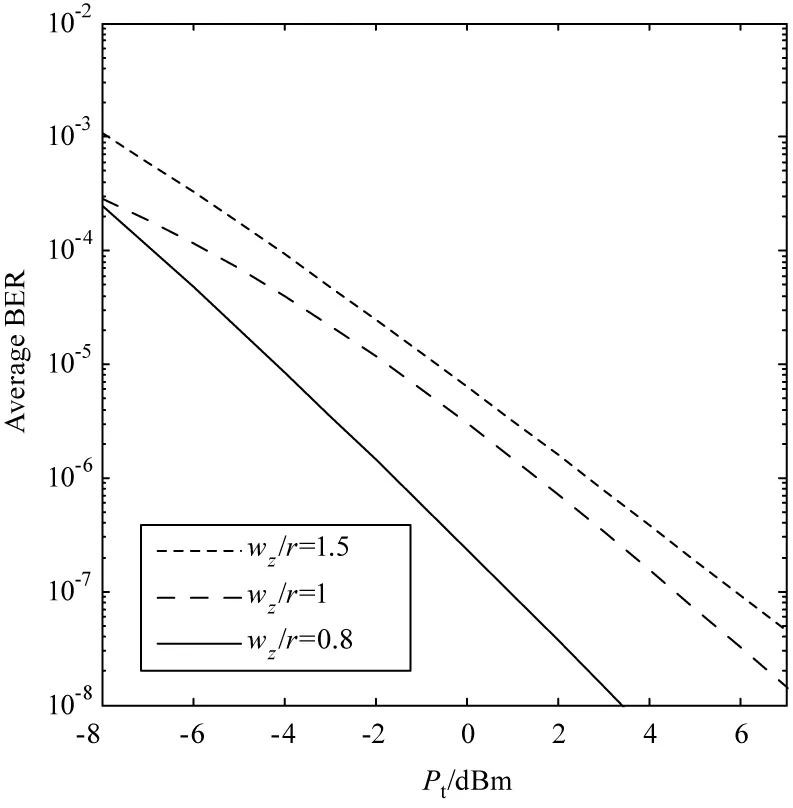
图6 当Cn2=1×10-14,M=4,σs/r=0.5时,不同wz/r比值下的平均误码率与发射功率的关系

5 结 论

本文以Exponentiated Weibull 分布为大气湍流衰减模型,联合指向误差及大气衰减因素推导出M-QAM调制下OFDM链路的平均误码率的闭合表达式,并根据表达式分别进行仿真分析了仅考虑大气湍流影响和联合考虑大气湍流及指向误差影响下不同性能参数对误码率的影响。由仿真分析可知,随着湍流强度加强、QAM调制阶数增大、接收端处波束宽度与接收机半径比值上升、接收端处波束宽度与接收机比值的增加,误码率随之增加,系统性能不断恶化。且指向误差对系统性能有明显的恶化作用,不考虑指向误差时发射功率对误码率的改善比考虑指向误差时提高了3个量级。在实际应用中,可以利用推导的性能闭合表达式,估计系统性能,为航空激光通信系统的设计提供参考。

[1] HU Hefei,LIU Yuanan.Application of high data-rate space laser communication system in aerospace information networks[J].Journal of Applied Optics,2011,32(6):1270-1290.(in Chinese)

胡鹤飞,刘元安.高速空间激光通信系统在空天信息网中的应用[J].应用光学,2011,32(6):1270-1290.

[2] LIU Hongjun.Overview of U.S.military airborne RFand FSO hybrid communication[J].Telecommunication Engineering,2014,54(12):1711-1716.(in Chinese)

刘红军.美军机载射频与FSO混合通信发展评述[J].电讯技术,2014,54(12):1711-1716.

[3] JIANG Huilin,AN yan,ZHANG Yalin,et al.Analysis of the status quo,development trend and key technologies of space laser communication[J].Journal of Spacecraft TT&C Technology,2015,34(3):207-217.(in Chinese)

姜会林,安岩,张雅林,等.空间激光通信现状、发展趋势及关键技术分析[J].飞行器测控学报,2015,34(3):207-217.

[4] Stotts L B,Plasson N,Martin T W,et al.Progress towards reliable free-space optical networks[C].Military Communications Conference,2011 - Milcom.IEEE,2011:1720-1726.

[5] Abdelmoula Bekkali,Chedlia Ben Naila,Kamugisha Kazaura,et al.Transmission analysis of OFDM-based wireless services over turbulent Radio-on-FSO links modeled by Gamma-Gamma distribution[J].IEEE photonics journal,2010,2(3):510-520.

[6] WANG Yong,CAO Jianian.Performance analysis of atmospheric laser communication system based on asymmetrically clipped optical orthogonal frequency division multiplexing intensity modulation[J].Acta Photonica Sinica,2011,40(1):36-40.(in Chinese)

王勇,曹家年.大气激光通信非对称限幅光正交频分复用技术[J].光子学报,2011,40(1):36-40.

[7] KE Xizheng,LEI Si Chen,LI Beilie.Experimental study on free space optical orthogonal frequency division multiplexing system [J].Chinese Journal of Lasers,2015,42(12):1205003-1-1205003-9.(in Chinese)

柯熙政,雷思琛,李蓓蕾.无线光正交频分复用系统的实验研究[J].中国激光,2015,42(12):1205003-1 - 1205003-9.

[8] Barris,R.and Dios,F.,Exponentiated Weibull distribution family under aperture averaging for Gaussian beam waves[J].Opt.Express,2012,20(12):719-721.

[9] Barris,R.and Dios,F.,Exponentiated Weibull model for the irradiance probability density function of a laser beam propagating through atmospheric turbulence[J].Optics & Laser Technology,2013,45(1):13-20.

[10] Mostafa A,Hranilovic S.In-field demonstration of OFDM-Over-FSO[J].IEEE Photonics Technology Letters,2012,24(8):709-711.

[11] Nistazakis H E,Stassinakis A N,Muhammad S S.et al.BER estimation for multi hop RoFSO QAM or PSK OFDM communication systems over Gamma-Gamma or exponentially modeled turbulence channels [J].Optics & Laser Technology,2014,(64):106-112.

[12] Ninositol M P,Nistazakis H E,Stassinakis A N,et al.Estimation of BER for a PSK OFDM RoFSO link with relays over exponentially modeled turbulence channels with pointing errors [C].3rd Pan-Hellenuic Conference on Electronics and Telecommunications,2015.

[13] Ninos M P,Nistazakis H E,Stassinakis A N,et al.BER estimation for a PSK OFDM RoFSO serially relayed link with pointing errors over gamma gamma turbulence channels [C].2nd International Conference on Electrical Engineering and Applications,2015.

[14] Adamchik V S,Marichev O I.The algorithm for calculating integrals of hypergeometric type functions and its realization in reduce system [C].International Conference on Symbolic and Algebraic Computation,1990:212-224.

[15] HAN Liqiang,YOU Yahui.Performance of free space optical communication with combined effects from atmospheric turbulence and pointing errors [J].Acta Optica Sinica,2014,34(11):1-6.(in Chinese)

韩立强,游雅晖.大气湍流及瞄准误差联合效应下自由空间光通信的性能[J].光学学报,2014,34(11):1-6.