规范混凝土材料本构关系扩展及验证
胡世强,卢云军,李江波,钟亚军
(1.浙江省建筑设计研究院,浙江 杭州 310006;2.浙江蓝城建筑设计有限公司,浙江 杭州 310030)
随着计算机技术的发展,有限元越来越多的应用在实际工程的弹塑性分析中,其中通用有限元ABAQUS具有应用广泛,非线性求解能力强的优点,更适于结构动力弹塑性响应分析。但ABAQUS自身的混凝土本构模型为多轴模型,这在非线性分析中会大大增加存储容量,且影响计算效率[1-5]。实际应用中结构体系的梁柱往往可以简化为单轴模型分析,以增加计算效率。本文依据现行规范,开发基于规范更为实用、效率更高的单轴模型,符合非线性分析的要求,并通过与试验数据对比,验证其有效性和准确性。
1 本构模型
1.1 混凝土本构模型
《混凝土结构设计规范(GB 50010—2010)》(以下简称规范)附录C在总结长期研究与试验结果的基础上,给出了混凝土单轴本构关系,本文此处略去规范给出的本构模型表达式。将规范本构模型绘制出图形,见图1和图2。
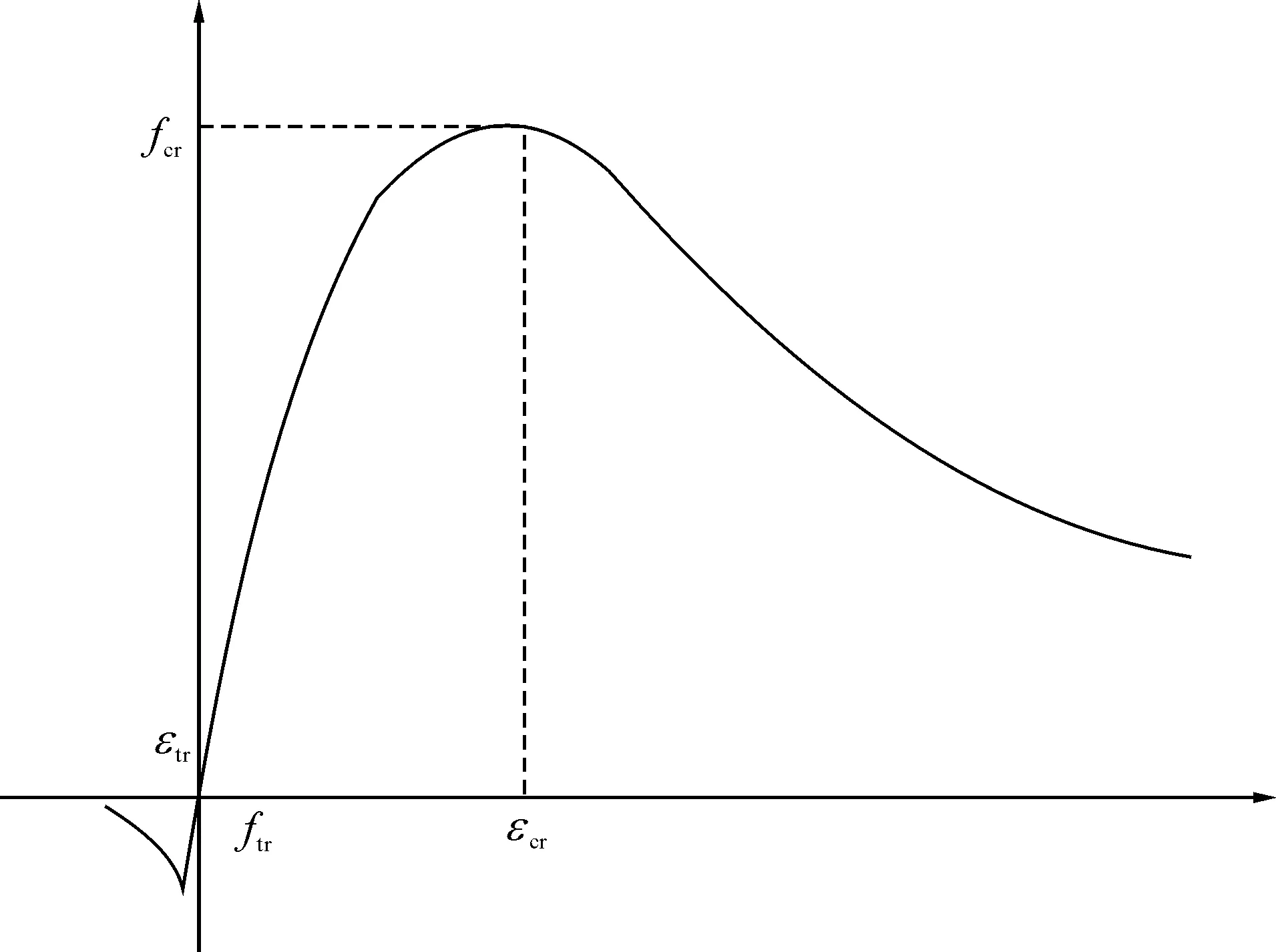
图1 混凝土单轴骨架曲线示意图
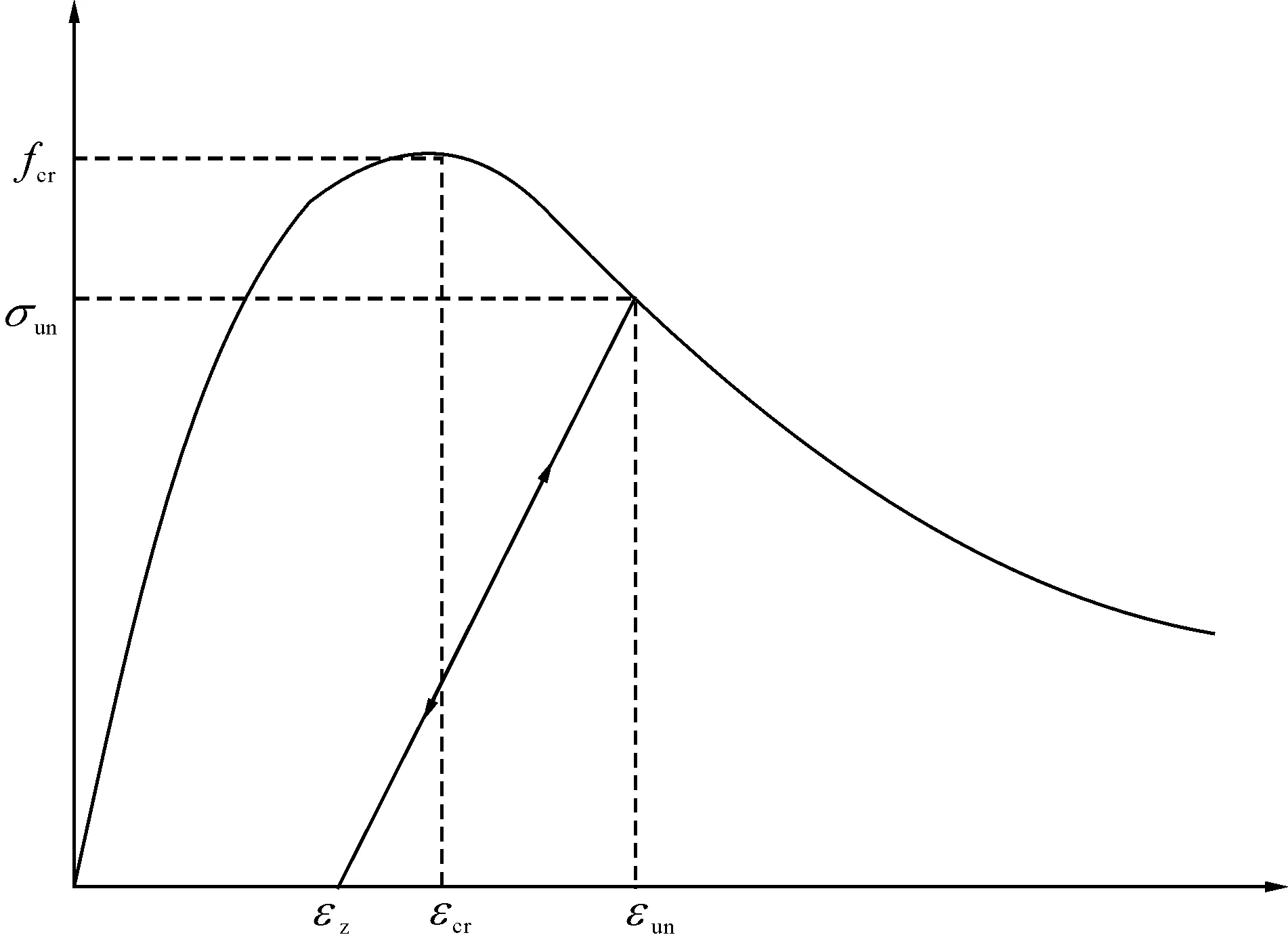
图2 受压混凝土卸载及再加载规则示意图
规范的本构模型没有混凝土受拉的卸载及再加载规则,且规范模型的受拉骨架曲线在拉应变超过峰值后,拉应力不为零。实际情况下混凝土在拉力作用下会产生较大的裂缝,此时混凝土已经丧失了承载力(应力为零)。因此本文模型参考OPENSEES中的Concrete02模型,对受拉下降段和受拉卸载准则进行补充修改,考虑受拉刚度退化和受拉损伤。
修改后模型描述如下:在峰值拉应力以前,曲线为规范建议公式,超过峰值应变后,混凝土开裂,进入线性下降段,斜率为Ets,超过极限应变后应力为零,表达式为式(1)至式(5)。受拉加卸载准则为:初次由A点进入受拉区后,沿骨架曲线加载值峰值点B,然后沿斜率Ets加载至C点,在C点发生卸载,沿CA回到A点再进入受压区。当第二次由A1点进入受拉区时,沿直线A1B1C1加载,此时A1B1与直线CA斜率相同,峰值点B1拉应力与上次卸载点C应力相同[6],受拉混凝土卸载及再加载准则示意图见图3。
受拉骨架曲线为:
εz≤ε<εt,r,σ=(1-dt)Ecε
(1)
dt=1-ρt(1.2-0.2x5)
(2)
(3)
εtr≤ε<εtu,σ=ftr-Ets(ε-εtr)
(4)
ε≥εtu,σ-0
(5)
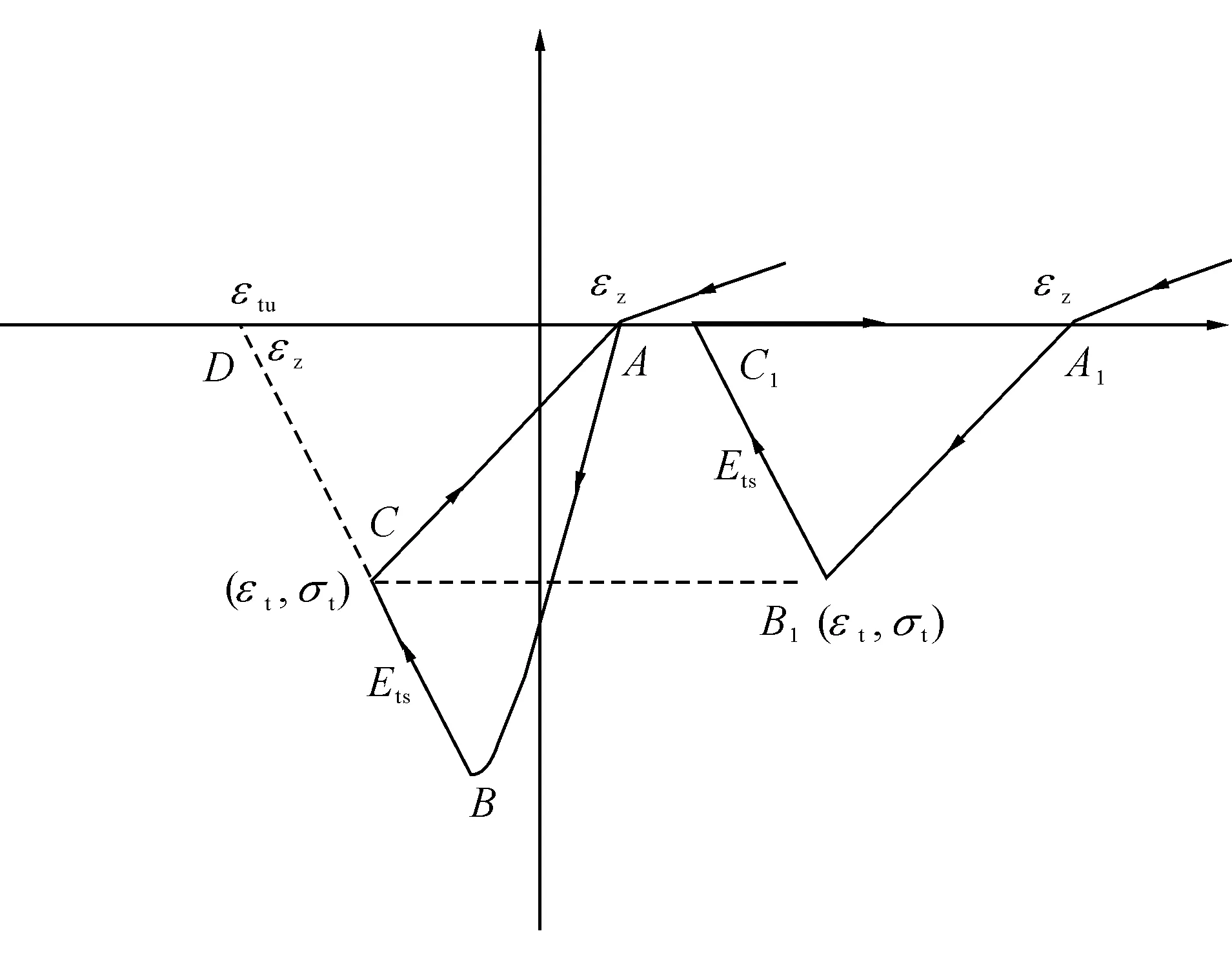
图3 受拉混凝土卸载及再加载规则示意图
本文参考Kent-Scott-Park模型考虑箍筋对混凝土的约束作用,公式可表示为[7]:
(6)
(7)
(8)
(9)
(10)
式中:qs为体积配箍率;
fyh为箍筋屈服强度;
h′为核心混凝土宽度(箍筋外皮之间的距离);
sh为箍筋间距;
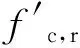
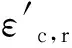
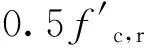
1.2 钢筋本构模型
钢筋的本构模型参考Clough提出的带有再加载刚度退化的双线性滞回模型,加载指向历史最大应变点,如果未屈服则指向屈服点。该模型能够考虑钢筋的硬化和Bauschinger效应。图4为钢筋本构模型的示意图,其加卸载路径为,首先沿初始刚度E0加载至屈服点A,再经过强化段加载至B点,卸载时按照初始刚度卸载至C点,然后反向沿CD加载至D点(D点为反向屈服点),再经过强化段反向加载至L点,沿初始刚度卸载至F点,然后正向加载至最大应变点(初始卸载点)B点,然后在经过强化段加载至G点,第二个循环沿初始刚度卸载至H点,然后反向加载到反向卸载点L(反向最大应变点),再经过强化段反向加载至J点,卸载时按照初始刚度卸载至K点,然后加载时指向最大应变点(G点)加载。
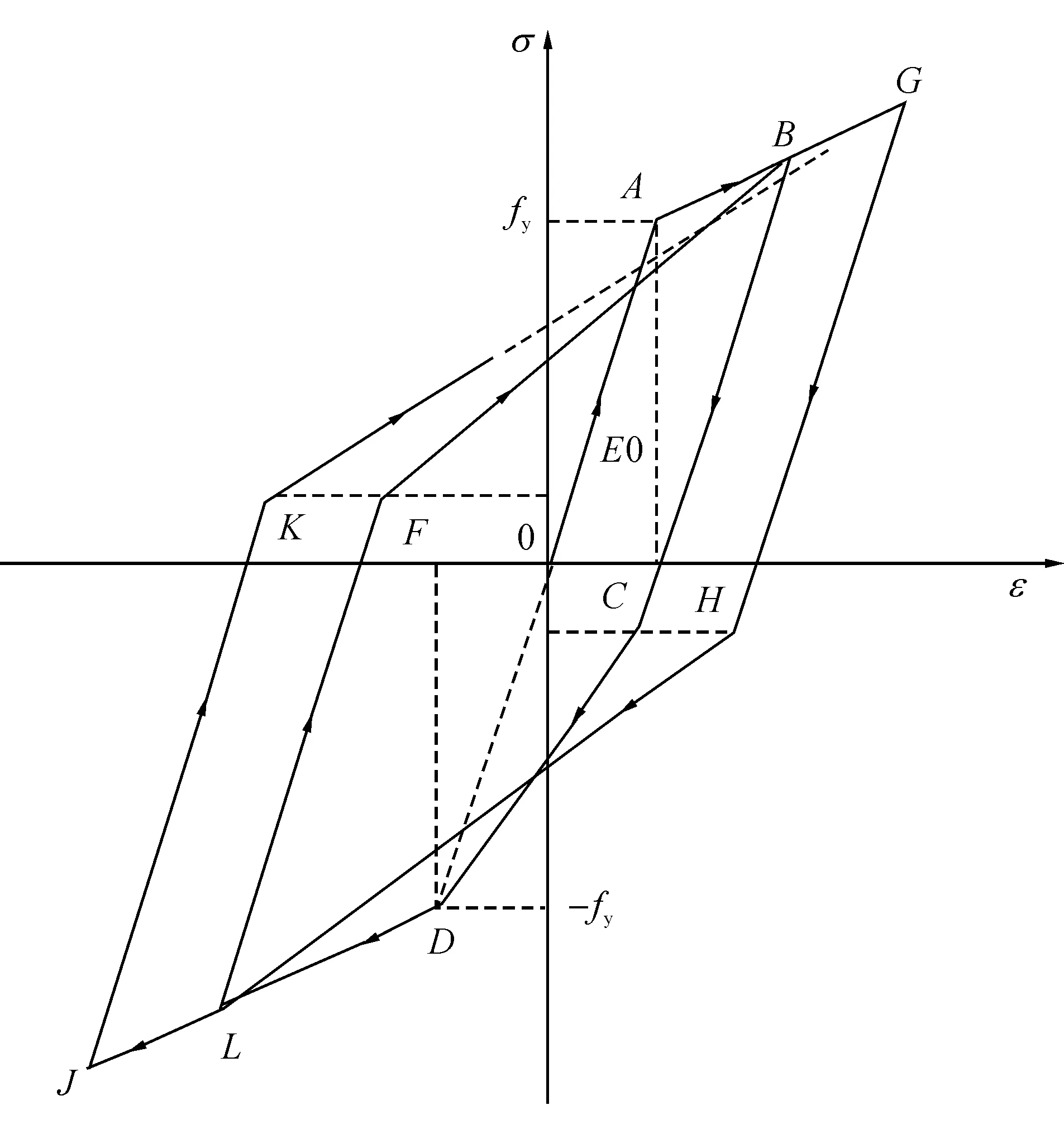
图4 钢筋本构模型示意图
2 单榀框架数值验证
本文采用的试验数据和试验结果均为2011年7月19日清华大学完成的整体框架拟静力倒塌试验分析竞赛公布的数据,它根据规范设计了一个3层4跨钢筋混凝土框架,本文通过ABAQUS建立试验模型,并使用本文编写的材料子程序进行模拟,最终校验本文子程序的准确性和有效性。
2.1 试验材料参数
试验实测得到的混凝土立方体强度平均值为fcu=32.6 MPa。钢筋的材料参数见表1。
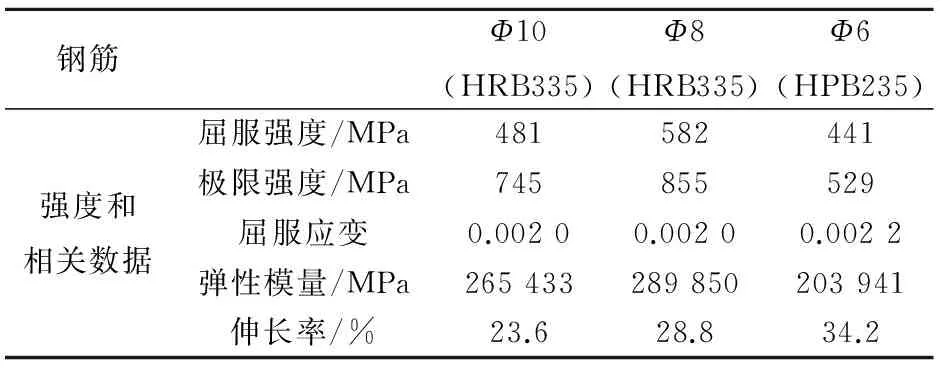
表1 钢筋强度表
2.2 框架试验情况
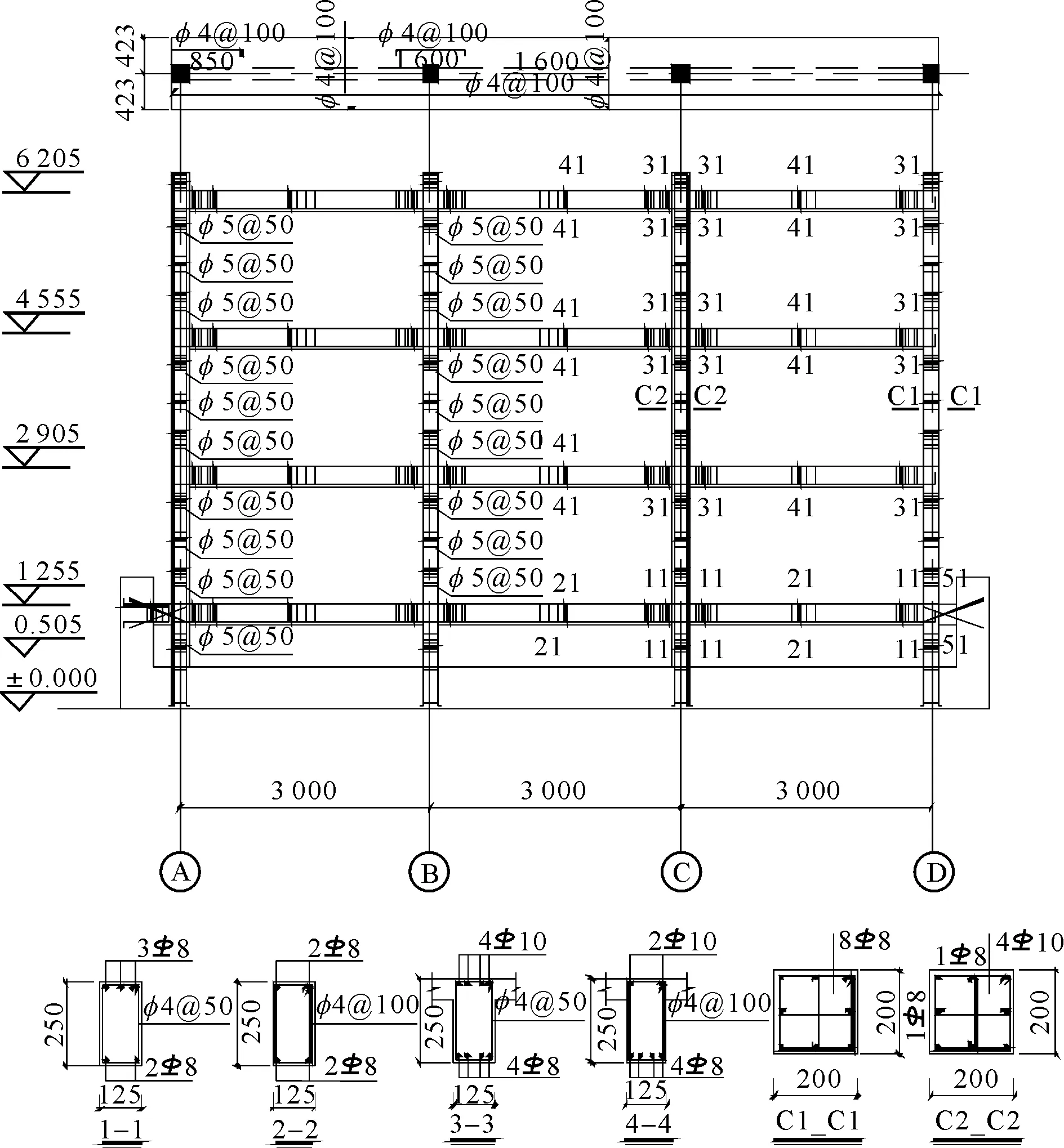
图5 框架尺寸及配筋详图
框架尺寸和配筋见图5,其中框架梁尺寸为125 mm×250 mm,两侧加悬挑板模拟楼板的影响,梁纵筋配筋率为0.7%,支座配筋率为1.1%。柱子尺寸均为200 mm×200 mm,其中中柱纵筋配筋率为1.29%,箍筋配箍率1.57%;边柱纵筋配筋率为1.00%,箍筋配箍率1.57%。试验装置见图6,柱轴力通过顶部的千斤顶施加,通过分配钢梁分配后中柱轴力为326 kN,边柱轴力为163 kN。作动器分别布置在一层二层和三层,图 7给出了加载的位移曲线,试验共进行了41个循环,其中一层最大位移为96 mm,二层最大位移为177 mm,三层最大位移为192 mm,最大层间位移角约为1/24。

图6 框架试验装置
2.3 ABAQUS数值模拟
通过ABAQUS建立框架的数值模型,模型示意图见图7,其中梁和柱单元都采用B31单元模拟,单元材料采用本文编写的VUMAT材料子程序,每个截面划分成5×5根混凝土纤维和16根钢筋纤维。
柱子轴力通过集中力模拟,中柱施加集中力326 kN,边柱施加集中力163 kN,保持集中轴力不变,在一二三层施加位移荷载,施加位移同图7所示,共施加41个循环,三层最大位移192 mm。
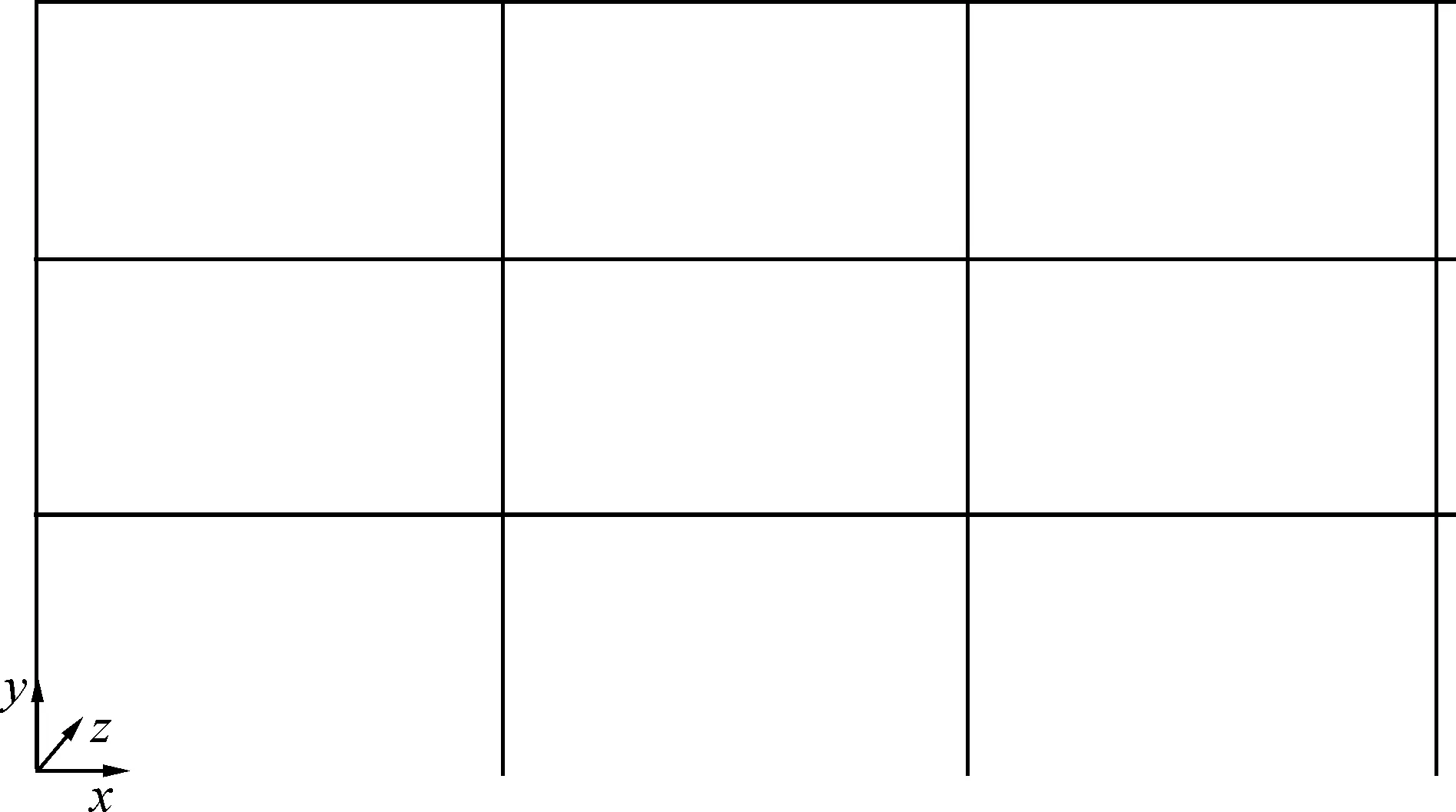
图7 数值模型示意图
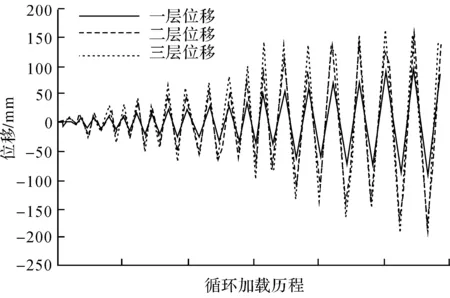
图8 框架加载情况图
根据委员会公布的顶层位移和基底反力数据,将试验数据和模拟结果绘制成顶点位移—基底反力滞回曲线,见图9,绘制骨架曲线见图10。
从图9计算结果和试验结果的对比看,滞回曲线呈现弓形,具有捏拢效应。这是由于框架结构在正向加载过程中构件的剪切变形产生了斜裂缝,在后续的反向加载中只需要较小的力即可使斜裂缝闭合,而在此过程中产生了较大的位移,滞回曲线因受到这样的滑移影响而呈现捏拢效应。从图9中还可以看出,滞回曲线的形状比较饱满,而且计算数值曲线与试验曲线吻合较好,反映出整个框架结构的塑性变形能力比较强,能较好地耗散地震能量。
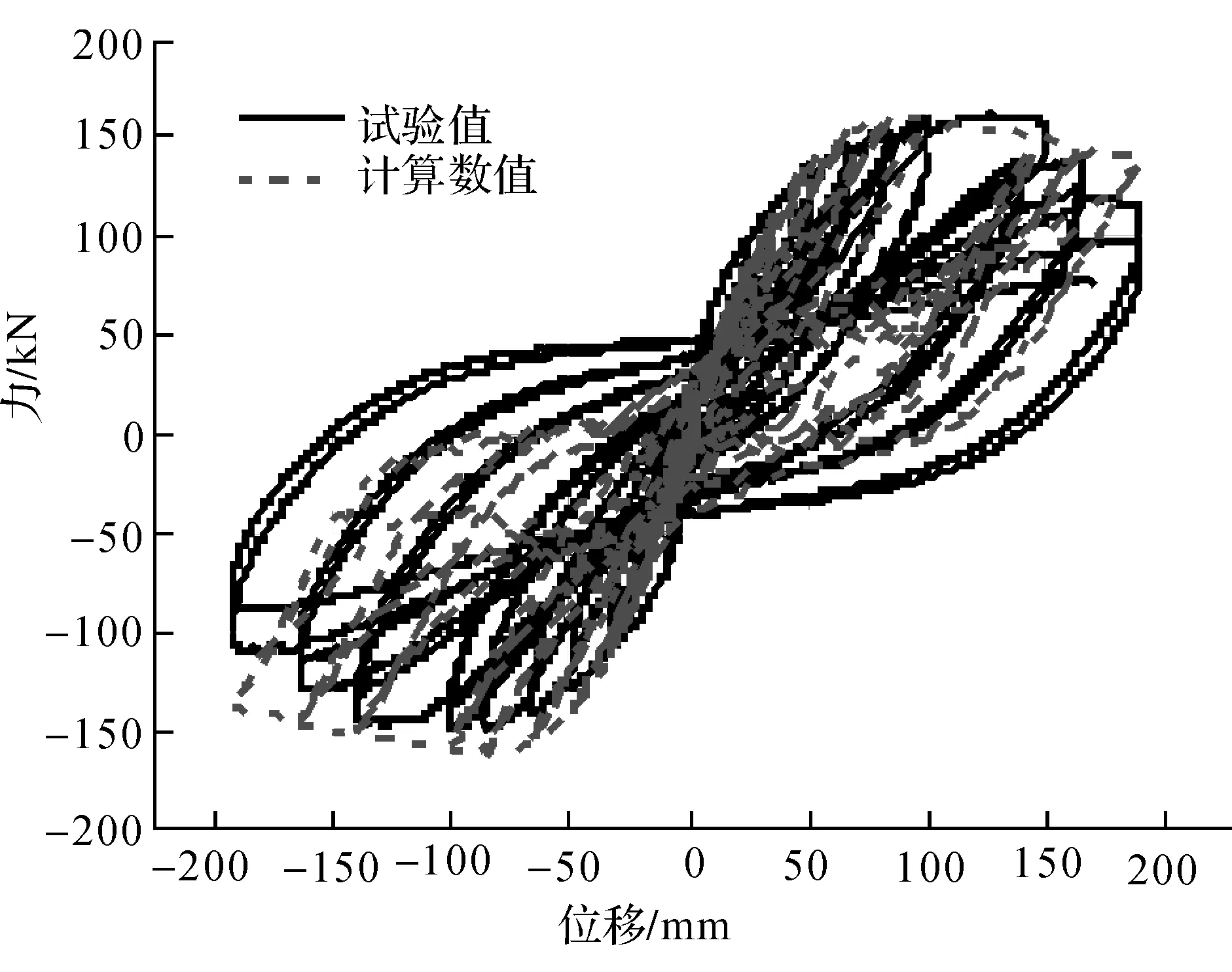
图9 顶点位移—底部反力滞回曲线
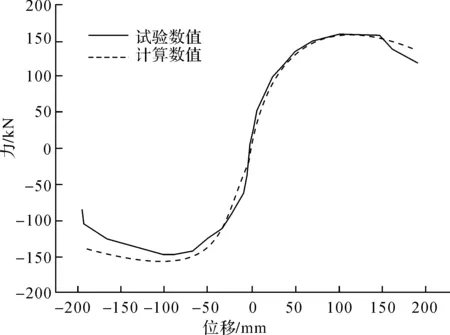
图10 骨架曲线对比图
从图10骨架曲线对比图中可以看出,计算结果与试验结果吻合度较好,在达到极限强度前,两条曲线基本一致;在达到极限强度后,试验曲线相比较曲率大,刚度和承载力下降得快,而模拟结果更为平缓,结构刚度下降速度没有达到试验结果,是后期需要对子程序改进的地方。
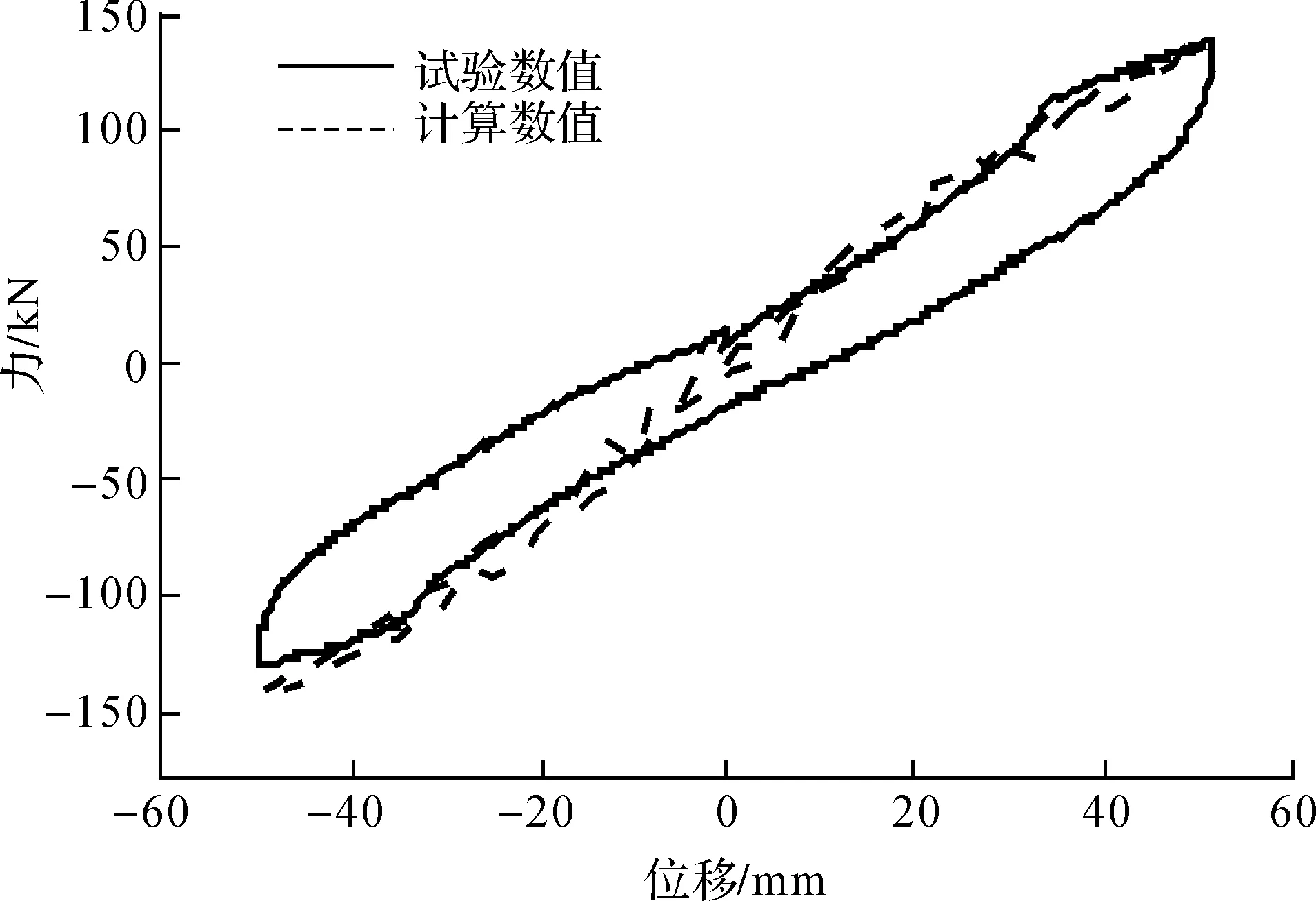
图11 加载至50 mm滞回环对比
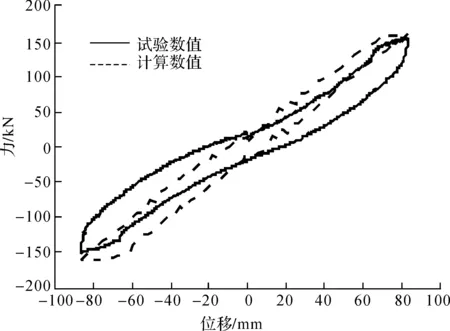
图12 加载至80 mm滞回环对比
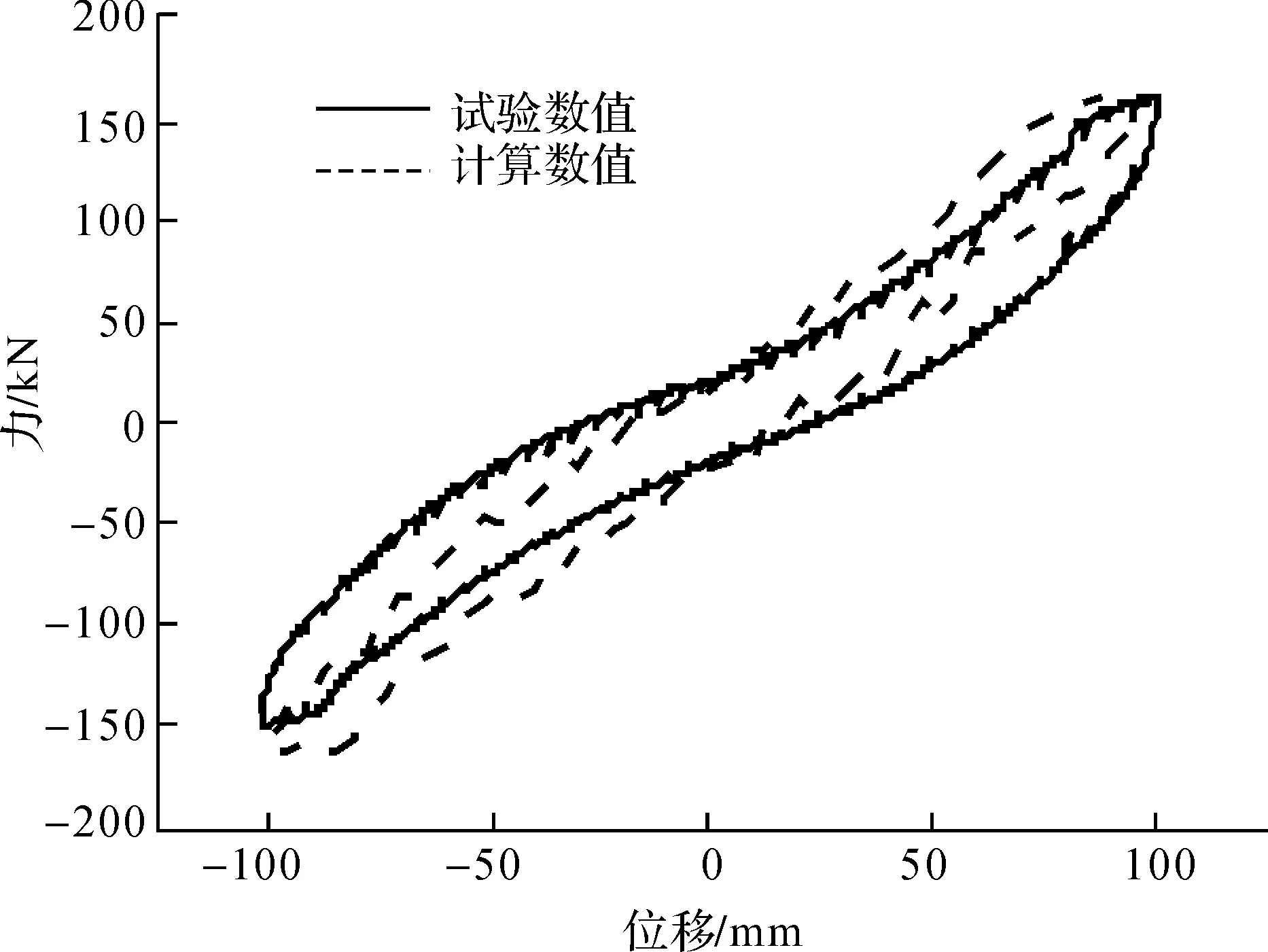
图13 加载至100 mm滞回环对比
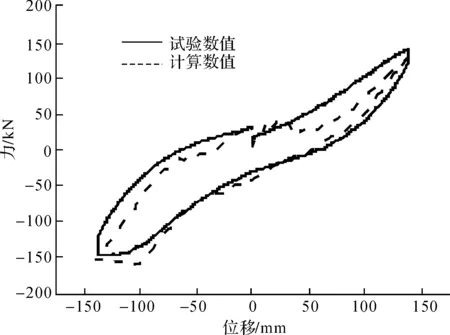
图14 加载至150 mm滞回环对比
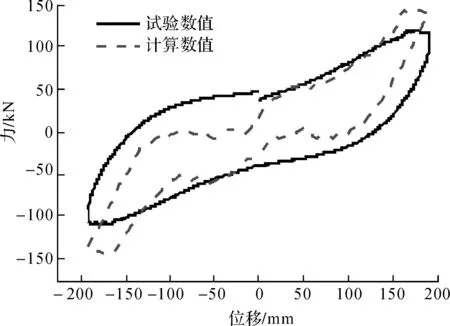
图15 加载至190 mm滞回环对比
图11至图15分别给出了结构在顶点最大位移分别达到50、80、100、150mm和190 mm时单个加载循环下的曲线对比,从这些图中可以看出,当顶点位移达到50 mm时(此时最大层间位移角约1/100),两者曲线相差较大,试验结果较计算结果形状饱满,这是由于材料试验钢筋的屈服应力较大,在顶点位移达到50 mm时只有部分钢筋达到屈服,因此计算结果刚度退化较慢,出现较大差异;当顶点位移达到80 mm和100 mm时(此时最大层间位移角分别约1/66和1/50),随着加载位移的增大,裂缝增大, 梁柱钢筋屈服,滑移影响逐渐明显,两条曲线形状呈现弓形,吻合度高;当位移进一步增大,达到150 mm(最大层间位移角约1/33)曲线的捏拢效应更加明显,两者吻合度较高;当位移增大至190 mm(最大层间位移角约1/20),捏拢效应更加明显,计算结果的承载力较试验值要高。
3 结 语
本文以ABAQUS有限元为平台,基于规范给出的混凝土本构关系,补充并完善加卸载本构模型开发出相应的VUMAT子程序,用于钢筋混凝土框架架构的数值模拟。通过与试验结果对比,本文所开发的材料本构模型能比较准确地模拟钢筋混凝土梁柱在往复荷载下的受力性能,可以用于钢筋混凝土梁柱单元的数值模拟。目前,相关研究人员对混凝土材料刚度退化和钢筋与混凝土之间的粘结滑移研究较少,存在进一步的完善空间。
[1] ABAQUS.ABAQUS user manual version 6.10[M]. Rhone Island:Pawtucket,2010.
[2] 齐虎,李云贵,周新炜.混凝土单轴滞回本构模型及ABAQUS二次开发[J].建筑科学,2014(3):812.
[3] 王强,朱丽丽,李哲,等.用于ABAQUS显式分析梁单元的钢筋本构模型研究[J].土木工程学报,2013,46(增刊):100105.
[4] 李正,朱炳寅,李宁.基于ABAQUS的钢筋混凝土框架结构地震损伤分析[J].建筑结构,2011,41(4):249252.
[5] 中国建筑科学研究院.GB 50010—2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社,2010.
[6] 陈伟.基于Opensees平台开发的混凝土滞回本构模型在结构分析中的应用[D].重庆:重庆大学,2012.
[7] 李安.考虑约束作用及率相关的混凝土单轴塑性损伤本构模型[D].哈尔滨:哈尔滨工业大学,2012.

