基于M atlab的图像信号降噪技术研究∗

宋翠薇 李 恺

（91180部队 大连 116041）

1 引言

图像是对客观事物最真实生动的表现，也是人们获取信息的重要方式，图像与人们的日常生活息息相关，人们已经将图像应用在各种领域中，如：工业监测、地质勘查、医学影像、智能机器人等。视频监控对图像的质量有着更高的要求，清晰的图像能够反映出更多的信息，但是，图像在采集、传输和处理的过程中都有可能被噪声污染。噪声会影响图像的主观视觉效果，降低图像数据层处理的质量和精度，影响人或者机器的判断。图像降噪处理的目的是对给定的图像进行有效的改善，提高图像的质量。本文采用了联合空间域和频域的降噪算法，能够保留图像的边缘信息和纹理信息，获得质量更高的图像。

2 图像噪声

图像的噪声在图像的采集和处理的全过程中都会产生，主要是由于器件的灵敏性，量化过程产生的误差等原因造成的。图像噪声会影响人体器官或者机器的感知系统对图像信息的接收和判断，噪声不仅会使图像的质量大幅度降低，使图像变得模糊，还会忽略图像的细节部分，给图像识别带来一定的困难。图像噪声按照与图像的相关性划分，可以分为加性噪声和乘性噪声。加性噪声与图像信号强度不相关，乘性噪声会随着图像信号的变化而变化。图像噪声按照成因可以分为热噪声、闪烁噪声、发射噪声和有色噪声。

噪声通常情况下是不可预测的，人们经常用概率统计的方法来认识和表示噪声，按照噪声概率密度函数（PDF）对噪声进行分类，噪声可以分为高斯噪声、均匀噪声、脉冲噪声、指数噪声、瑞丽噪声和伽马噪声，本文重点介绍前三种噪声。

2.1 高斯噪声PDF

高斯噪声的概率密度函数服从高斯分布，在数学上比较容易处理，高斯随机x的概率密度函数为

式中，x为像素强度，μ为x均值，σ为x的标准差，σ2为x的方差。

高斯噪声的概率密度函数图像如图1所示。

2.2 均匀噪声PDF

均匀噪声密度经常用作随机数发生器的基础，其灰度值的分布在一定范围内是均衡的，均匀噪声的概率密度函数为

式中：均值为 μ=(a+b)/2，方差 σ2=(b-a)2/12。

均匀噪声的概率密度函数图像如图2所示。

2.3 脉冲噪声PDF

脉冲噪声又称为椒盐噪声，概率密度函数为

式中，x表示像素强度值，a和b表示图像中的极限强度值。

3 图像降噪效果评价标准

图像的降噪效果可以采用主观评价和客观评价两种评价手段，主观评价采用对比观察方法实现对图像降噪效果的评价，客观评价采用客观的评价指标实现对图像降噪效果的评价。主观评价采用人眼观察图像的降噪效果，通过对比滤波后图像与原始图像之间的差异，对比不同的滤波方法图像降噪质量。图像降噪质量评价主要考虑在噪声平滑和细节保护两个方面的效果，注重图像的细节信息，例如尖角、边缘、细小纹理等。

客观评价采用客观的数据标准衡量图像的降噪效果，可以根据需要采用多种评价指标，例如均方误差（Mean Square Error）、归一化均方误差（Nor⁃malized Mean Square Error）、平均绝对误差（Mean Absolute Error）、归一化平均绝对误差（Normal Mean Absolute Error）、峰 值 信 噪 比（Peak sig⁃nal-to-Noise Ratio），本文采用峰值信噪比作为降噪效果的评价标准。

式中，f(i，j)表示原始无噪声图像在(i，j)位置上的灰度值，h(i，j)表示降噪后图像在(i，j)位置上的灰度值，图像的尺寸大小为M*N。

4 常用降噪技术

图像降噪算法主要可以分为空间域和频域两种降噪算法，空间域降噪算法主要是利用图像所处的空间，利用滤波器直接作用于图像本身，降噪过程中，滤波器访问图像中每一个像素点，利用某种规则对像素值进行处理，产生降噪后的图像。常见的空间域图像降噪算法主要包括双边滤波、中值滤波、均值滤波以及维纳滤波。双边滤波采用局部加权平均的方法获得重建后的复原图像像素值，中值滤波基于排序理论，能够对非线性的信号噪声进行滤除，均值滤波属于线性滤波，采用邻域平均值法进行滤波，维纳滤波是基于最小均方误差准则、对平稳过程的最优滤波方法。

频域降噪算法是将空间域转换到频域，可以采用傅里叶变换、小波变换、离散余弦变换等方法，傅里叶变换和小波变换是最常用的频域降噪算法。在频域内，图像的信息可以表现为不同频率分量的组合，图像信息在频域的分布特征表现的非常直观，只要抑制噪声所在的频率能量就能够实现降噪的目的。基于频域的滤波根据消除的频率分量特征可以分为低通滤波、高通滤波和带通滤波。小波算法是一种时频局部化的算法，采用合适的小波基函数对信号进行多层分解，利用阈值量化处理，然后重构图像信号。小波算法可以滤除噪声的同时，保留图像的细节信息。

除了空间域和频域的图像降噪算法，基于高斯滤波和偏微分方程之间的联系，出现了基于偏微分方程的滤波算法，主要可以分为曲率驱动扩张方法、张量及扩散方法和变分法。

5 基于空间域和频域的降噪算法

本文采用了基于空间域和频域相结合的降噪方法，空间域滤波选用双边滤波器，频域采用小波阈值降噪算法。空间域双边滤波算法具有操作简单、易迭代和局部化的特点，能够对滤波后的对象的图像边缘信息很好保存，高斯滤波和维纳滤波对图像细节的保护能力不强，双边滤波属于空间分布的高斯滤波函数，降噪时可以保留图像的边缘信息。频域上，基于小波阈值的降噪算法具有良好的性能，可以根据降噪需要选择不同的阈值，从而达到理想的降噪效果。本文设计的结合空间域和频域的降噪算法流程如图3所示。

双边滤波器属于非线性滤波方法，结合图像空间邻近度和像素值相似度的一种折中化的处理，在图像降噪的过程中综合考虑空间域信息和灰度相似性，能够达到保留边缘信息的目的。在边缘附近，距离较远的像素不会影响边缘的像素值，从而能够很好地保持边缘附近的像素值，通过卷积过程中结合空间域函数和值域函数能够实现边缘保持的目的。

小波阈值降噪中阈值的选取对于降噪效果具有重要的影响，传统的硬阈值、软阈值在图像降噪中都存在着一定的缺陷。硬阈值函数在阈值点不连续，容易在奇异点处出现明显的Pseudo-Gibbs现象。采用软阈值函数对信号进行降噪处理，降噪后的信号同原始信号存在的一定偏差。本文选取一种改进的阈值函数：

式中，n为调节参数，当n=0时，改进的阈值函数可以得到原信号，当n趋近于无穷时，改进阈值趋近于软阈值。随着调节参数选用的不同，改进阈值介于硬阈值和软阈值之间，更好地满足图像降噪的要求。

6 降噪效果对比

为了验证图像降噪效果，本文选取视频监控中的截图检验不同图像降噪算法的降噪效果，对比采用空间域、频域以及空间域和频域相结合的图像降噪算法的效果。原图和降噪后的图像如图4所示。

7 结语

本文重点研究图像噪声的分类、来源，以及常用的图像降噪算法，通过调研发现图像降噪算法中，空间域算法对降噪后的图像内容细节信息保留不好，频域算法对降噪后的图像边缘信息保存不完整。本文结合空间域和频域算法，提出联合降噪算法，进行图像降噪效果的对比，从而验证算法的有效性。

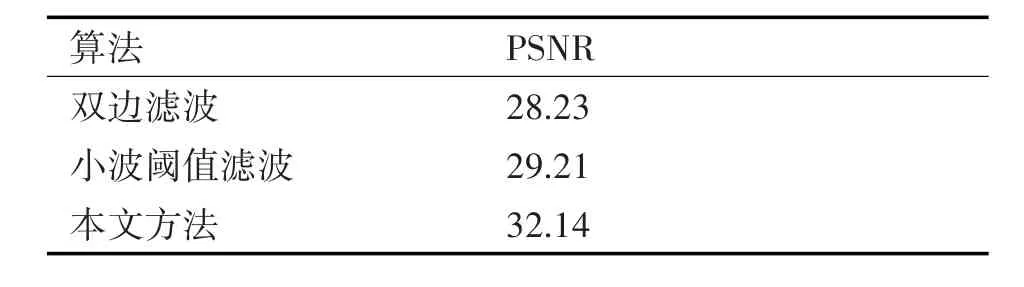
表1 不同方法降噪效果对比

［1］张聚，王陈，程芸.小波与双边滤波的医学超声图像降噪［J］.中国图象图形学报，2014，19（01）：126-132．

［2］于万波.基于MATLAB的图像处理［M］.北京：清华大学出版社，2008：20-62．

［3］刘玉淑.基于多尺度变换的图像降噪及融合算法研究［D］.济南：山东大学，2013．

［4］马国兵.基于小波变换的图像降噪技术研究［D］.杭州：浙江理工大学，2013．

［5］王彬.MATLAB数字信号处理［M］.北京：机械工业出版社，2010：17-53．

［6］林清馨，吕祚坤，梁潇.基于小波收缩的噪声图像恢复新型算法实现与验证［J］.电子设计工程，2011，19（24）：158-160．

［7］林红章，石澄贤.一种自适应双边滤波的超声图像降噪［J］.江南大学学报（自然科学版），2010，9（02）：169-172．

［8］徐长发，李国宽.实用小波方法［M］.武汉：华中科技大学出版社，2009：51-86．

［9］刘贵忠.小波分析及应用［M］.西安：西安电子科技大学出版社，1994：1-55．

［10］袁运能，毛士艺.基于离散小波标架的信号降噪［J］.信号处理，1999，15（3）：204-210．

［11］元海燕.数字图像处理的关键技术及应用［J］.信息系统工程，2017（01）：93-99．

［12］吴国荣.数字图像处理的发展现状与趋势研究［J］.中国新通信，2017（03）：55-62．