多轴载荷下结构细节疲劳强度额定值确定方法
王晓玮,尚德广,熊健
多轴载荷下结构细节疲劳强度额定值确定方法
王晓玮1,尚德广1,熊健1
(北京工业大学 机电学院,北京, 100124)
提出一种在多轴载荷下确定结构细节疲劳强度额定值的方法。基于单轴双点法细节疲劳强度额定值(DFR)确定方法,在多轴载荷下,首先利用高周多轴疲劳损伤模型求出其等效应力幅(等效拉伸应力幅或等效剪应力幅),结合Goodman方程,把等效应力幅转换为应力比=0.06时的最大正应力,最终确定多轴条件下的细节疲劳强度额定值。通过7075-T651铝合金薄壁管进行单轴疲劳试验,确定单轴细节疲劳强度额定值,并进行多轴疲劳试验,包括比例加载和非比例加载。采用该方法预测多轴载荷下的DFR值,对比单轴试验的DFR值,相对误差的绝对值在10%左右。该方法确定多轴条件下的结构细节疲劳强度额定值具有较好的效果。
细节疲劳强度额定值;双点法;多轴疲劳试验;多轴高周疲劳
疲劳失效是飞机零部件失效的主要形式,因此疲劳强度设计也成为了现代飞机设计中不可或缺的重要环节。结构件细节疲劳强度额定值(DFR)是指在应力比=0.06,置信度为95%,可靠度为95%的要求下,结构能承受105次循环所对应的最大名义应力值(疲劳强度),也就是说,DFR值是结构满足上述条件的条件疲劳强度,是材料本身固有的疲劳特性特征值。DFR法不仅设计简单,还兼顾了可靠性和置信度要求,是较好的疲劳寿命预测方法之一。因而,该方法在航空结构疲劳强度与耐久性设计中得到广泛应用。
关于DFR法的理论和应用已有一定的研究[1-5]。由于DFR法是在单轴条件下提出的,相关研究主要集中在单轴疲劳领域。在多轴载荷下,DFR方法的研究比较少。由于结构件形状、受力形式等的影响,实际服役中结构件受力往往是多轴的,因此研究多轴加载条件下的DFR值确定方法具有重要的工程应用价值。
DFR值确定方法有双点法、单点法等,双点法对DFR值估算更加准确。文中在单轴双点法DFR值确定方法的基础上,提出了多轴载荷下DFR值的确定方法。该方法可将现有的高周多轴模型应用于确定多轴载荷下的DFR值。最后采用铝合金7075-T651薄壁管件进行了单轴拉伸和拉-扭多轴疲劳试验,结合高周多轴疲劳模型,利用该方法预测多轴DFR值,并与单轴的DFR试验值进行了比较。
1 多轴DFR确定方法
1.1 基于双点法的单轴DFR确定方法
双点法要求在应力比为=0.06的条件下,分别在=104~105周寿命区间确定一个应力水平1,测定一组寿命数据;在为105~106周寿命区间确定一个应力水平2,测定一组寿命数据。通过如下步骤确定结构件的DFR值:
1)对两个应力水平1和2的两组试验寿命数据分别根据式(1)求得特征寿命β和β:

式中:为特征寿命;为同一试验加载条件组内进行试验的次数;为材料常数,取=4;N为同一试验加载条件组内的第个试验结果寿命。
2)根据两组试验数据的特征寿命12,分别计算可靠度=95%,置信度=95%的寿命95/95:

式中:95/95表示可靠度为95%,置信度为95%的寿命;T为试样系数;R为可靠度系数;C为置信度系数。
3)1条件下的95/95寿命记为1,2条件下的95/95记为2。在双对数坐标下利用两点拟合一条-曲线,寿命为105次循环对应的应力水平即为材料的DFR值,如图1所示。

图1 DFR值确定示意图
1.2 提出的多轴DFR确定方法
现有的高周多轴疲劳模型往往是将多轴载荷转换为应力比=-1的拉伸或者剪切应力幅,而DFR值是应力比=0.06下的轴向最大正应力值。因此,高周多轴模型不能直接求出多轴条件下的等效DFR值。文中提出通过如下应力转化的方法,基于双点法在多轴加载条件下求出DFR值,计算步骤如下。
1)对试验数据利用选取的多轴高周疲劳模型计算等效应力幅eq,a。若多轴疲劳模型求得的是等效拉应力幅eq,a,则:

若多轴疲劳模型求得的是等效剪应力幅eq,a,则需要转换成等效拉应力幅。根据Mises理论,转换公式为:

2)利用Goodman模型,将eq,a转化为=0.06时的最大应力eq,0.06:
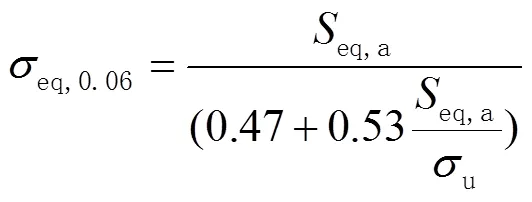
式中:u为材料的拉伸强度。
3)利用1.1节所述单轴双点法确定DFR值。
2 高周多轴疲劳模型
目前,基于不同的方法,研究者提出大量的多轴高周疲劳模型[6-7],主要有基于临界面法模型[8-13]、基于应力不变量法模型[14]和基于细微观法模型[15-16]等。临界面的概念是在疲劳裂纹萌生和扩展机理上建立起来的,具有一定的物理意义。因此,在多轴疲劳研究中,广泛采用基于临界面法的多轴疲劳模型。文中利用基于临界面法的模型[12-13],结合提出的方法,预测多轴DFR值。
2.1 试件应力状态分析
对于光滑薄壁管件,在拉扭复合加载条件下,其应力状态如图2所示,加载的应力向量为:
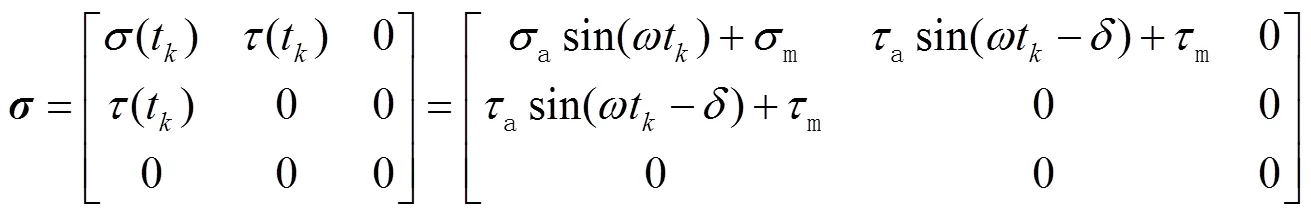
式中:tk为时间点,k=1,2,…,N;σa为加载的轴向应力幅值,MPa;σm为加载的轴向应力均值,MPa;τa为加载的剪切应力幅值,MPa;τm为加载的剪切应力均值,MPa。
如图2所示,对于任意平面,其位置可由角度和表示,即(,)。其中,是平面的法向向量与轴所成的角度,是平面的法向向量在-面上的投影与轴所成的角度。根据斜截面公式,可以求得平面上的剪应力和正应力。
临界面c(c,c)是指裂纹萌生所在面,是平面(,)的特殊情况。在拉扭复合加载下,裂纹在试件表面萌生,即c=±90°。因此,确定临界面c(c,c)的位置就是确定角度c的值。平面(,)的应力可简化为二维应力问题,其应力为:

式中:σ为平面(,)上的正应力;τ为平面(,)上的剪应力。
根据式(7),可以求得最大绝对剪应力和所在面的角度:
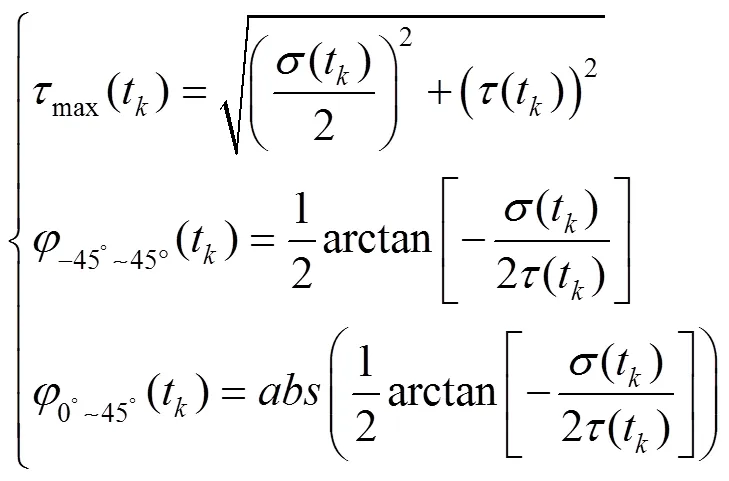
2.2 确定临界面位置
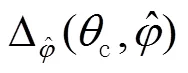
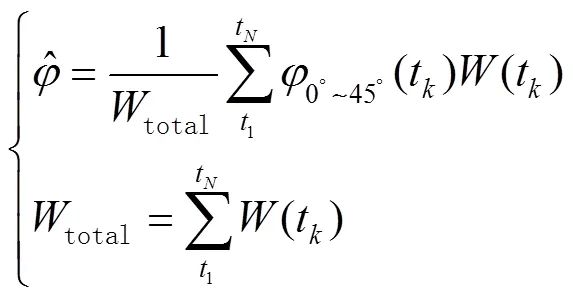

确定临界面位置c(c,c)的具体计算步骤如下所述。


2.3 高周多轴疲劳模型
基于权函数所确定的临界面,本文采用文献[13]的高周多轴疲劳模型:
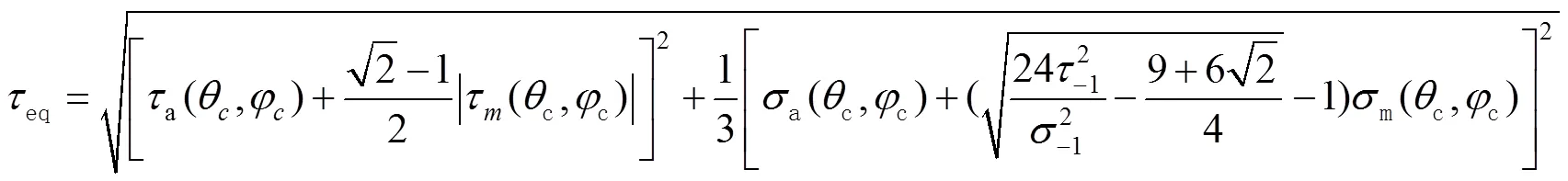
试验研究表明,平均正拉应力减小疲劳寿命,平均正压应力延长疲劳寿命。为了保证平均正应力的有效影响,该模型适用于满足以下条件的材料:

3 疲劳试验
3.1 基本试验条件和材料
试验采用电液伺服MTS858多轴疲劳试验机,试验频率为10 Hz。试验材料选择7075-T651铝合金,该材料具有高强度、轻质量等特性,是目前在航空航天领域得到广泛应用的结构材料。该材料的化学成分和静力学性能分别见表1和表2。材料的拉伸疲劳极限-1和剪切疲劳极限-1分别为207.06,116.77 MPa。

表1 7075-T651铝合金化学成分 %

表2 7075-T651铝合金室温静力学性能
试件形状为薄壁管试件,其中,试验段外壁的直径为12.5 mm,内壁的直径为10.5 mm,试验段的长度为30 mm,壁厚为1 mm。综合考虑试件尺寸和试验设备的要求,试件的形状和具体尺寸如图3所示。

图3 疲劳试件形状及尺寸
3.2 单轴和多轴疲劳试验
在试验中,疲劳载荷的加载波形设定为正弦波。试验是由轴向力和扭矩控制。对于薄壁管试件,可以通过计算求得其轴向应力和试件表面的剪切应力,具体的计算方法为:
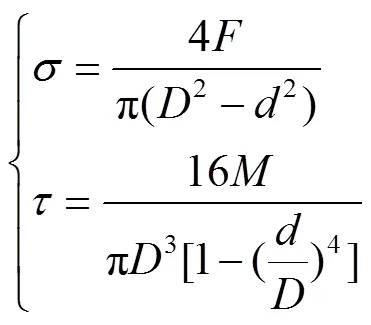
式中:为轴向拉力,N;为扭矩,N·m;为薄壁管试验段外径,该试验中=12.5 mm;为薄壁管试验段内径,该试验中=10.5 mm
单轴疲劳试验是在应力比=0.06条件下进行的。试验选取两个应力水平,一个应力水平进行三组试验,具体试验结果见表3。
拉-扭多轴疲劳试验的拉伸和扭转应力分量的应力比均为=0.06,相同的应力水平也进行三次试验。具体的试验加载参数和试验结果见表4。

表3 单轴试验加载条件及寿命结果

表4 多轴试验加载条件及寿命结果
4 试验结果分析
DFR是基于单轴疲劳提出的,但在实际工程中,服役中的结构件通常都是在多轴应力状态下工作的。在这种情况下,单轴DFR值不能直接应用于工程实际中。
文中提出通过将多轴应力等效为单轴应力的方法,获得多轴加载下等效的单轴DFR值。因此,拉扭复合加载作用下等效的DFR与单轴拉伸作用下的DFR应该相同。以单轴试验的DFR值为基准,验证提出的多轴DFR确定方法的效果。
在该试验中,式(2)中试样系数T取值为1,对铝合金材料可靠度系数R取值为2.1,每组试验件为3根,置信度系数C取值为1.195。采用单轴双点法,利用试验中两组单轴试验数据,可以计算出单轴DFR试验值为DFR=395 MPa。
通过多轴条件下预测的等效单轴DFR值与单轴试验得到的DFR值对比,分析该方法的预测效果。预测结果见表5,其中相对误差计算为:

式中:eq,DFR为预测的多轴DFR值,MPa;DFR为材料的单轴DFR值,DFR=395 MPa。
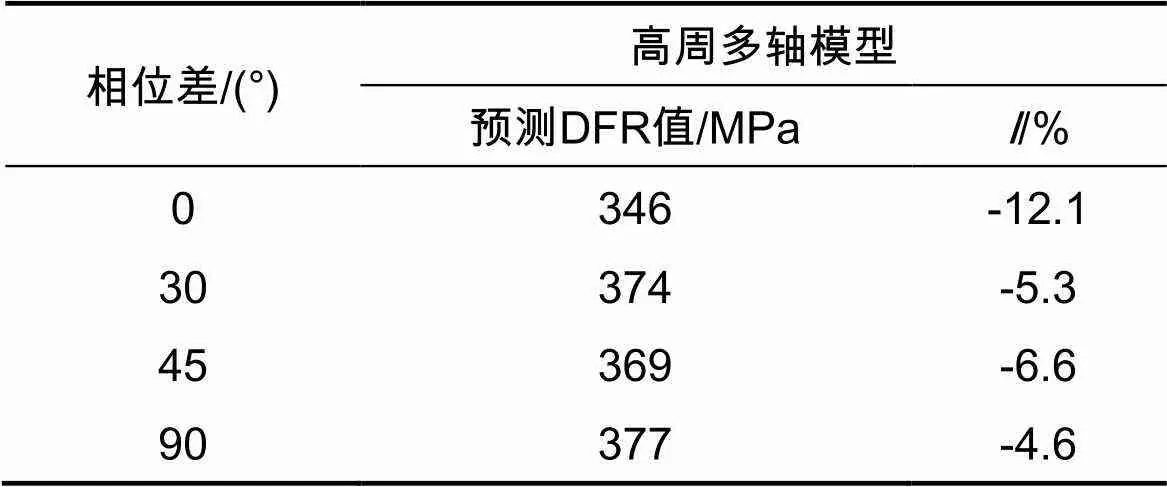
表5 多轴载荷下DFR值预测结果
从表5可以看出,利用文中提出的方法,在多轴条件下预测的DFR值相对于单轴DFR试验值误差绝对值基本在10%左右。从结果可以看出,多轴条件下利用该方法预测材料的DFR值可以取得较好的效果。
5 结论
1)采用7075-T651铝合金进行恒幅单轴和多轴疲劳试验,并通过应力比=0.06的单轴疲劳试验,确定材料的DFR值。
2)基于单轴双点法确定DFR值的方法,文中提出了一种在多轴载荷条件下,材料DFR值确定方法。
3)结合高周多轴疲劳模型,利用文中提出的方法可以预测多轴加载条件下DFR值。通过预测的多轴DFR值和单轴DFR试验值对比,结果表明提出的方法具有较好的预测效果。
[1] HUANG W, WANG T J, GARBATOV Y, et al. DFR Based Fatigue Reliability Assessment of Riveted Lap Joint Accounting for Correlations[J]. International Journal of Fatigue, 2013, 47: 106-114.
[2] 鲍蕊, 张建宇, 郑晓玲, 等. DFR腐蚀影响系数及其试验测定[J]. 北京航空航天大学学报, 2006, 32(6): 639-644.
[3] 郑晓玲, 鲍蕊, 费斌军. 综合环境下民机机身典型长桁接头疲劳分析[J]. 北京航空航天大学学报, 2007, 33(4): 379-382.
[4] 董彦民, 刘文珽, 杨超. 军用飞机结构耐久性设计的细节疲劳额定值方法[J]. 航空学报, 2010, 31(12): 2357-2364.
[5] 董彦民, 贺小帆, 刘文珽. 基于不同寿命分布的DFR值换算关系[J]. 北京航空航天大学, 2011, 37(12): 1525- 1528.
[6] PAPADOPOULOS I V, DAVOLI P, FILIPPINI M, et al. A comparative Study of Multiaxial High-cycle Fatigue Criteria for Metals[J]. International Journal of Fatigue, 1997, 19: 219-235.
[7] PAPUGA J. A Survey on Evaluating the Fatigue Limit under Multiaxial Loading[J]. International Journal of Fatigue, 2011, 33(2): 153-165.
[8] CARPINTERI A, SPAGNOLI A, VANTADORI S. Multiaxial Fatigue Assessment Using a Simplified Critical Plane-based Criterion[J]. International Journal of Fatigue, 2011, 33: 969-976.
[9] CARPINTERI A, RONCHEI C, SPAGNOLI A, et al. Lifetime Estimation in the Low/Medium-cycle Regime Using the Carpinteri-Spagnoli Multiaxial Fatigue Criterion[J]. Theoretical and Applied Fracture Mechanics, 2014, 73: 120-127.
[10] CARPINTERI A, RONCHEI C, SPAGNOLI A, et al. On the Use of the Prismatic Hull Method in a Critical Plane-based Multiaxial Fatigue Criterion[J]. International Journal of Fatigue, 2014, 68: 159-167.
[11] SUSMEL L. Multiaxial Fatigue Limits and Material Sensitivity to Non-zero Mean Stresses Normal to the Critical Planes[J]. Fatigue and Fracture of Engineering Materials and Structures, 2008, 31: 295-309.
[12] WANG X W, SHANG D G. Determination of the Critical Plane by a Weight-function Method Based on the Maximum Shear Stress Plane under Multiaxial High-cycle Loading[J]. International journal of fatigue, 2016, 90: 36-46.
[13] WANG X W, SHANG D G, CHEN H. Multiaxial High-cycle Fatigue Life Prediction Model Considering Mean Shear Stress Effect under Constant and Variable Amplitude Loading[J]. Theoretical and Applied Fracture Mechanics, 2017, 76: 134-143.
[14] CRISTOFORI A, SUSMEL L, TOVO R. A Stress Invariant Based Criterion to Estimate Fatigue Damage under Multiaxial Loading[J]. International Journal of Fatigue, 2008, 30: 1646-1658.
[15] GUERCHAIS R, ROBERT C, MOREL F, et al. Micromechanical Study of the Loading Path Effect in High Cycle Fatigue[J]. International Journal of Fatigue, 2014, 59: 64-75.
[16] ESLAMI R, RIESCH-OPPERMANN H, KRAFT O. Prediction of Multiaxial High Cycle Fatigue at Small Scales Based on a Micro-mechanical Model[J]. International Journal of Fatigue, 2016, 83: 66-74.
Determination of Detail Fatigue Rating of structure under Multiaxial Loading
WANG Xiao-wei, SHANG De-guang, XIONG Jian
(College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China)
To propose a method for determining Detail Fatigue Rating (DFR) of structure under multiaxial loading.Based on the two-point method for uniaxial loading (DFR), the high-cycle multiaxial fatigue test model was adopted to obtainthe equivalent stress (equivalent tensile stress or equivalent shearing strength). The equivalent stress was transferred to the equivalent tension stress under=0.06 through the Goodman equation, to determine the detail fatigue rating under multiaxial loading. The equivalent stress was determined by employing a multiaxial high-cycle fatigue model. According to the uniaxial fatigue tests for 7075-T651 aluminum alloy under=0.06, the DFR for uniaxial loading was determined. Then, the multiaxial fatigue tests were conducted, including the proportional and non-proportional loadings.From the comparisons between the predicted DFR for multiaxial loading and the experimental DFR for uniaixal loading, the absolute value of the relative errors was about 10%.The proposed method, for the determination of the DFR under multiaxial, has a good predictive capability.
detail fatigue rating; two-point method; multiaxial fatigue test; multiaxial high-cycle fatigue
TJ02
A
1672-9242(2018)03-0092-06
10.7643/ issn.1672-9242.2018.03.019
2018-01-15;
2018-02-07
国家自然科学基金(11272019, 51535001, 11572008)
王晓玮(1988—),女,河北人,博士研究生,主要从事高周多轴疲劳、高温疲劳方面的研究。
尚德广(1962—),男,博士,教授,主要从事机械结构耐久性设计、多轴疲劳强度、有限元研究。

