输油管道中缺陷快速定位的应力波技术

刘凯 黄玉玲

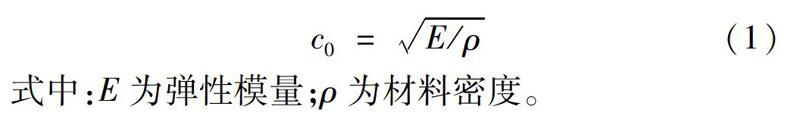
摘要：为解决输油管道中裂纹缺陷难于快速定位的问题，基于应力波的特性研究应力波无损检测技术在管道缺陷检测中的应用。借助ANSYS AUTODYN建立多组动态仿真模型，计算并分析仿真结果数据，对比光滑无裂纹缺陷的管道与含有裂纹缺陷管道的应力波传播规律。经过分析应力波的传播变化过程，得出管道裂纹对应力波的干扰规律，进而得到2种利用应力波进行无损检测的方法：一是沿着管道轴向布置测点的检测方法；二是在管道截面布置测点的检测方法。

关键词：无损检测； 应力波； 管道缺陷； 动态仿真； 结构安全

中图分类号：TE9

文献标志码：B

文章编号：1006-0871（2018）01-0048-07

Abstract： In order to solve the problem that it is difficult to position the oil pipeline defects rapidly， a new nondestructive detection method based on stress wave is studied utilizing the characteristics of stress wave. Many dynamic simulation models are built using ANSYS AUTODYN to calculate and analyze the simulation result data. The stress wave propagation rule is compared between the smooth pipeline without crack defects and the pipeline with crack defects. The propagation and change process of stress wave is analyzed， the interference rule of the pipeline crack in the stress wave is obtained， and the nondestructive detection method using stress wave is obtained： one method is to arrange the measuring points along the pipeline axis， the other is to arrange the measuring points at pipeline cross sections.

Key words： nondestructive detection； stress wave； pipeline defect； dynamic simulation； structural safety

0 引 言

管道結构失效多是由微小缺陷逐渐扩展变大引起的，这些微小缺陷都是细小瑕疵在外界物理或者化学的作用下萌生变化形成的。裂纹按其萌生与扩展机理，可分为许多种类。[1]由于材料本身不可避免地存在一些微小缺陷，这些缺陷在外荷载的作用下扩大、连接、扩展，往往造成管道失效破坏。所以，无损检测对结构的质量控制和安全使用起着举足轻重的作用，各个行业都积极探索使用这一技术。

目前，无损检测方法主要有超声波法、射线透照法、磁粉法、渗透法和管材涡流检测法等。[2-4]尽管无损检测技术发展迅速，但是对大型管道缺陷的初步定位仍存在很大的困难。

根据应力波在介质中的传播特性，若在传播途中遇到气孔、裂纹等缺陷形成的结构不连续处，则会发生反射、折射等传播方式的改变，应力波信号对结构的不连续处有高度的敏感性。王秀彦等[5]利用脉冲回波法发展管道超声导波检测技术，并测试使用中管道的缺陷。该技术在被测构件的某一位置激发出频率和传播方向已知的应力波，利用压电晶片接收传播回来的应力波，然后分析波形特征，计算应力波因子，此因子可以表示脉冲应力波的传播途径和效率。使用这种方法可以检测构件在结构完整性和本构性质上的变化。AZARI等[6]在隧道检测中运用应力波无损检测技术检测混泥土材料的完整性，但局限于小范围检测。SHIOTANI等[7]应用应力波频率分析对混凝土平板上的缺陷进行定位。HUANG等[8]应用应力波检测桩基的完整性。CHEN等[9]通过研究波的频率，将应力波检测技术应用于民用基础设施安全检测。

本文研究应力波在管道中的传播变化规律，采用杆撞击的简单方式进行动态加载产生应力波。由于输油管道的尺寸大、成本高，所以采用计算机仿真技术进行研究。[10-11]对比分析光滑无裂纹管道与含裂纹管道中的应力波变化规律，得出2种大型管道中缺陷裂纹的无损检测方法：一是沿着管道轴向布置测点的检测方法；二是在管道截面布置测点的检测方法。

1 应力波理论与AUTODYN

1.1 应力波理论

波是外部扰动在介质中的传播[12]，扰动所携带的能量在介质中传播，传播的速度叫做波速，通常记作c。根据介质的性质不同，波的传播速度也不同。扰动使得处于静止的质点开始运动，但是由于周围有介质的阻碍，质点并不会流向其他位置，只是在其平衡位置附近运动，运动的速度叫做质点运动速度，记作v。事实证明，质点运动速度远小于波的传播速度。在固体材料中，由于波速非常快，波动现象仅仅在微妙、毫秒级的时间内发生。

质点运动方向与波的传播方向一致的波叫做纵波，如一维杆中的应力波，应力波的波速只与材料本身有关，与应力的大小无关，杆中的应力纵波波速为

在有限长的介质中，应力波的传播必然面临反射、透射问题。在有限长一维弹性杆中，波动方程的一般解为

式（4）表明，右行波应力与质点的速度符号相反，而左行波应力符号与质点的速度符号相同，由此可以分析应力波的反射问题。

相向而行的2个应力波传播示意见图1。由于弹性波的控制为线性方程，所以两波相遇时可以线性疊加。同号应力波相遇后，波形重合部分的应力为2个应力波的和，符号不变，质点速度为两者之差，符号与绝对值较大者相同，见图1a）。如果2个相向的应力波应力符号相反，那么重合部分的应力为2个应力波的差，符号与其中绝对值较大者相同，速度为两者之和，见图1b）。当2个波分离后，各自按照各自的波形继续传播。如果2个相向传播的应力波应力值相同、方向相反，那么两波相遇后应力值为0，其质点速度加倍。由此可以设想：在图1a）的AB截面位置应力加倍、速度为0，就相当于是杆的固定端，而在图1b）的CD截面应力为0、速度加倍，就相当于是杆的自由端。

由以上分析可知：波由固定端反射后，应力会增大至入射波的2倍，质点速度为0，波的性质不变，压缩波反射后仍然是压缩波，拉伸波反射后仍然为拉伸波；波在自由端反射后，应力减小至0，质点速度增大为入射端的2倍，波的性质也会改变，拉伸波反射后为压缩波，压缩波反射后为拉伸波。

1.2 ANSYS AUTODYN仿真技术

随着计算机硬件的不断发展，数值模拟方法和计算机软件不断完善，数值模拟已经成为很多研究的有效途径。目前，动态数值模拟方法主要包括有限差分法、有限单元法、无网格离散元法和边界元法等。众多数值模拟方法各有千秋，有限单元法是应用较广的方法之一。该方法的主要优点是材料界面行为及其历史可得到清晰描述，分析结构的形状变化与有限网格的变化一致，物质不会在单元与单元之间发生流动。但是，用拉格朗日网格算法求解高速冲击或爆炸载荷下的裂纹扩展问题会涉及大变形问题，其有限网格可能产生严重扭曲，不仅需要网格重构，而且会严重影响计算精度。在裂纹动态扩展过程中，裂纹的扩展方向不能事先确定，因此在计算过程中需要不断地重新划分网格以模拟裂纹的动态扩展过程。鉴于拉格朗日数值方法的缺陷，无网格的数值模拟算法得到发展和应用，光滑粒子流体动力学（smoothed particle hydrodynamics， SPH）方法是无网格数值方法中的一种，其计算公式较为简单，计算效率较高，所以被广泛应用于解决工程问题。在SPH方法数值模拟过程中需计算粒子间的相互作用，与网格或单元数目相当的网格方法相比，SPH方法计算时间较长，所以通常将SPH算法与基于网格的算法耦合（在大变形区域应用SPH方法，而在小变形区域应用基于网格的算法）模拟高速冲击等问题。

ANSYS 15.0的AUTODYN分析系统是显式非线性动力分析系统，可以解决高度非线性动力学问题，拥有有限元、有限体积和无网格法等多个求解器，同时包括多种材料模型和参数数据。在AUTODYN中，材料的应力状态可以分成2部分：一部分是由静水压力引起的体积变化；另一部分是由偏应力引起的形状变化。因此，材料的本构模型可以描述为3部分：状态方程、强度方程和失效模型。

状态方程在AUTODYN软件中反映材料的体积变形能力，用来计算体积应力。静水压力、比容和比能之间的关系可以表示为

强度模型可以通过应力和应变的关系描述材料抵抗变形的能力，用以计算偏应力。常用的强度模型有Elastic，von Mises，Johnson-Cook，Drucker-Prager和Johnson-Holmquist等准则。von Mises准则基于试验结果提出，由于静水应力状态对岩石材料的屈服和体积变形有影响，所以该准则对岩石类材料适用性较差。Drucker-Prager准则在von Mises准则条件的基础上提出，Johnson-Cook准则主要用于高速冲击、高温以及一些高度非线性的材料变形。

失效模型用以描述材料的破坏，材料在力的作用下逐渐变形，当达到一定条件时出现材料失效。AUTODYN中有主应力失效、主应变失效、塑性应变失效和Johnson-Cook失效等模型。

2 仿真模型和可靠性分析

2.1 仿真模型

2.1.1 几何模型

按照研究目的，将整体模型分成2部分：一部分是受冲击加载的含裂纹管道，另一部分是形成冲击载荷的冲击部件。冲击部件为实心圆柱体，直径150 mm，长度500 mm；管道外径110 mm，内径100 mm，长度10 000 mm。对于含裂纹的管道，裂纹位置位于距离管道受冲击端4 800 mm的位置，裂纹平面与管道截面平行，裂纹形状类似于圆环的一部分，裂纹两端的夹角为90°，裂纹厚度为1 mm。仿真计算几何模型见图2。

2.1.2 网格划分

网格划分质量对动态有限元分析计算效率影响很大，为确保计算精度和提高计算效率，采用六面体单元网格。网格划分的工具有许多种，例如ICEM，ANSYS Mesh，HyperMesh等。ICEM通过分块映射的方法能够得到理想的网格，但是对于超长管道，操作起来非常困难；ANSYS Mesh可以通过曲线或近似控制的方法快速划分网格，但在很大程度上属于计算机自动控制，很难控制网格的形状；HyperMesh能够很好地处理裂纹尖端形状，控制网格形状、大小等，虽然网格划分操作较繁琐，但网格质量较高。所以，本项目所有仿真模型的网格都采用HyperMesh划分。

2.1.3 初始条件、边界条件和计算控制

冲击杆的冲击部件在一定速度的冲击下产生应力波，管道和冲击部件均采用低碳结构钢，材料密度为7 896 kg/m-3，初始冲击速度为2 m/s，管道的边界为自由边界，管道上等距布置检测点（高斯点）提取对应位置上的物理量，通过这些物理量进行应力波波形分析。

2.2 仿真结果可靠性分析

2.2.1 应力波传播过程

应力波随时间传播过程示意见图3。

在图3a）～3c）中，压缩应力波沿管道向右传播；当应力波到达右端边界的时刻，根据应力波的传播理论，压缩波在右端反射形成同等大小的拉伸波向左传播，即图3d）和3e）。仿真结果中的应力波传播符合理论和实际的应力波传播规律。

2.2.2 应力波波速

应力波波速计算示意见图4。2号测点到18号测点的距离为8 000 mm。从2个测点的应力变化曲线可知，应力波在0.488 ms时刻到达2号测点，在1.959 ms到达18号测点，其间用时为1.471 ms，由此可计算应力波的纵波波速。

为定量分析，计算应力波的传播波速。在实际情况下，根据材料不同，钢的应力纵波波速一般为5 000～6 000 m/s。由图4可知，仿真结果的应力波波速为5 438.48 m/s，符合实际钢材的应力波波速，由此进一步说明前文数值仿真结果的可靠性。

2.2.3 应力波形分析

应力波形示意见图5。选取管道中间位置10号测点的应力波形进行分析。

应力波形首先是压缩的波峰，然后是拉伸的波谷，形成的原因就是冲击形成的压缩波经过自由端反射形成拉伸波。图中实际波形为鋸齿形，这些锯齿是由于冲击杆中也存在应力波的来回反射，是拉伸波到达冲击接触面的时刻引起管道中压缩波的减小导致的。此外，压缩波峰与拉伸波谷的时间差为1.9 ms，已计算得到应力波的波速为5 438.48 m/s，可计算得到应力波的传播矩离为10 333 mm，实际情况是10 000 mm，误差仅为3.33%。以上分析说明，本文的数值仿真模型和计算结果符合实际情况，可作为应力波无损检测技术探索研究的思路。

3 应力波无损检测技术

3.1 含裂纹管道与无裂纹管道上应力波的差异对比

3.1.1 对比分析模型建立

仿真对比模型示意见图6。

2根长度为10 000 mm的管道，其中一根为无裂纹光滑管道，另一根为含裂纹的管道，裂纹位置距离冲击端4 800 mm。冲击端设置相同的冲击杆，冲击速度为0.5 m/s，材料均选用低碳结构钢，由此形成对比模型。选取管道上1、5、9、13、17号测点的应力数据为分析对象，对比分析不同管道应力值的变化。

3.1.2 对比分析结果

分别对不同管道上各测点处的压力、x轴应力、y轴应力和z轴应力进行对比，见图7。

由图7可以看出：在不同管道中，9号测点存在明显差异；在含裂纹的管道中，除9号测点的应力值存在差异外，其他测点波形基本相似。导致9号测点应力波形差异的原因是9号测点位于裂纹附近区域，距离裂纹只有300 mm。这种差异的存在是应力波无损检测的基础，利用这种差异可以推断裂纹所在的位置。

3.1.3 沿着管道轴向布置测点的检测理论

在含裂纹的管道中，靠近裂纹区域的x轴应力和y轴应力相对于其他区域有明显差异，可以利用此特点进行管道裂纹的位置确定。

沿着管道方向等距离布置测点，按照精度要求、材料成本和仪器设备等因素确定测点间距，间距越小裂纹缺陷的定位精度越高，当然材料成本也随之升高，对测量仪器的通道要求也更多。在各个测点粘贴动态应变片，考虑到裂纹方向的随机性，应沿着管道轴向和横向各粘贴应变片，通过轴向动态加载提取测量数据，对比各测点上轴向和横向应力曲线，存在明显差异的曲线对应的测点就是裂纹所在的位置。如果测点密度过低，由于远离裂纹的各个测点上的应力波曲线没有明显差异，那么可能无法判断出裂纹的存在。

3.2 含裂纹管道同一横截面上应力值差异分析

3.2.1 分析模型

建立含裂纹的管道模型，为避免管道边界对应力波的影响，管道长度取20 000 mm，其他初始条件、边界条件和材料等设置与上文对比分析模型相同。沿截面布置测点示意见图8。在距离裂纹7 300 mm位置的横截面上对称设置4个测点，对比4个测点沿轴向和周向的应力。

3.2.2 结果对比

同一截面测点周向和轴向应力对比分别见图9和10。由此可以看出：同一截面测点上周向应力错综复杂，轴向应力在开始阶段基本重合，在区域A出现差异，但是区域A差异出现的起始点不容易确定。为最大化这一差异，以某一个值为基准，计算其他测点相对于基准点的应力值差的绝对值之和，便可以放大差异。例如，以应力的平均值为基准，求应力值差的绝对值之和为

3.2.3 在管道截面布置测点的无损检测理论

在没有裂纹存在时，截面处4个不同测点上的应力值非常接近；在有裂纹存在时，经过裂纹的干扰后返回的应力波在截面不同测点上产生差异。为最大化差异，计算各测点应力值与平均值差值的绝对值之和见图11。由此可以看出，AB区段图形显示十分密集，即是由裂纹干扰引起的差值之和变化频率高的区段。

沿管道的某一截面对称设置观测点，然后沿轴向和横向在测点上粘贴动态应变片，通过轴向动态加载，提取各个测点的应力值；考虑到裂纹方向的随机性，进行扭转加载，同样提取测点应力值。将各点应力值整理，求出其差值的绝对值之和，确定曲线密集区段的起始时刻，即图11中t1时刻，同时可以确定应力波经过截面的初始时刻t0，然后通过式（7）计算得到Δ，即测点布置截面到裂纹的距离，并由此得出裂纹位置。

4 结 论

根据应力波的传播理论，当应力波在结构中传播时，经过裂缝、小孔等不连续处，就会发生反射、折射、散射等波的效应，只要通过探测获取到这些波的变化信息，就能够推导出裂纹的存在及其位置。

基于应力波的特性研究应力波无损检测技术在管道缺陷检测中的应用，得到2种在管道中进行应力波无损检测的方法：一是沿管道轴向布置测点的方法，这种方法优点是能够直观地确定裂纹所在的位置，可检测出多个裂纹，但是耗材较大、成本较高；二是在管道截面布置测点的方法，此方法优点是便捷省材、成本低，缺点是仅能检测出距离测量截面最近的裂纹，后续其他裂纹无法检测。

参考文献：

[1] 项智. 锅炉压力容器压力管道检验中的裂纹问题[J]. 石油和化工设备， 2011， 14（10）： 51-53. DOI： 10.3969/j.issn.1674-8980.2011.10.016.

[2] 贾鹏军， 罗金恒， 刘琰， 等. 石化成品油外输管道泄漏的无损检测[J]. 无损检测， 2016， 38（3）： 11-13. DOI： 10.11973/wsjc201603004.

[3] 刘胜， 骆苏军. 基于超声导波技术的长输管道无损检测[J]. 无损检测， 2015， 37（6）： 40-42. DOI： 10.11973/wsjc201506010.

[4] 徐春广， 王俊峰， 宋剑峰， 等. 油气管道焊接残余应力超聲无损检测与原位调控技术[J]. 石油科学通报， 2016， 1（3）： 442-449. DOI： 10.3969/j.issn. 2096-1693. 2016.03.040.

[5] 王秀彦， 金山， 李涌， 等. 应力波在管道中传播的实验研究[J]. 实验力学， 2004， 19（1）： 97-102. DOI： 10.3969/j.issn.1001-4888.2004.01.018.

[6] AZARI H， NAZARIAN S， YUAN D. A case study on tunnel lining assessment using stress wave-based nondestructive testing methods[C]//Proceedings of Geo-Congress 2014. Atlanta， 2014： 439-452.

[7] SHIOTANI T， OHTSU H， MOMOKI S， et al. Damage evaluation for concrete bridge deck by means of stress wave techniques[J]. Journal of Bridge Engineering， 2012， 17（6）： 847-856. DOI： 10.1061/（ASCE）BE.1943-5592.0000373.

[8] HUANG Y H， NI S H. Experimental study for evaluation of stress wave approaches on a group pile foundation[J]. NDT & E International， 2012， 47（7）： 134-143. DOI： 10.1016/j.ndteint.2012.01.006.

[9] CHEN J， ZHANG L. Health monitoring of civil infrastructure systems-the stress wave approach[C]//Proceedings of 2012 Prognostics and System Health Management（PHM） Conference. Beijing： IEEE， 2012： 1-5. DOI： 10.1109/PHM.2012.6228957.

[10] 陈金龙， 阎军， 卢青针， 等. 深水柔性管道铺设过程的动态仿真[J]. 计算机辅助工程， 2017， 26（4）： 7-13. DOI：10.13340/j.cae.2017.04.002.

[11] 陈健， 雷铮强， 王富祥， 等. 基于有限元法的含凹陷油气管道应变分析[J]. 计算机辅助工程， 2015， 24（5）： 59-62. DOI： 10.13340/j.cae.2015.05.012.

[12] 宁建国. 爆炸与冲击动力学[M]. 国防工业出版社， 2010： 54-63.

（编辑 武晓英）