动车组车体铝型材隔声性能分析

熊剑春，贾尚帅

(中车唐山机车车辆有限公司 产品研发中心，河北 唐山 063035)

0 引言

随着动车组运行速度的提高，噪声干扰问题凸显，尤其是车内噪声对旅客的乘坐舒适性产生较大的影响[1],动车组的低噪声设计首先要完成声学总体指标的制定和验证[2]，其中车体大部件铝型材既是主要承载结构，同时也是车体隔声的关键组成[3- 4].车体铝型材的研究主要集中在隔声量的仿真和试验[5- 6]，文献[7]通过结构分析、振动分析和声学特性分析，对铝型材的减振降噪进行评估和优化.

本文针对动车组车体大部件铝型材结构，使用混合FE-SEA方法、SEA方法，分频段建立隔声仿真模型，进行隔声预测分析，并和试验结果进行对比验证.使用验证后的铝型材隔声仿真模型，对其隔声量的影响参数进行对比，分析面板、筋板的厚度、筋板型式、整体高度对其隔声性能的影响.

1 隔声系统统计能量分析基本理论

1.1 统计能量分析理论

统计能量法是基于能量的观点来求解振动系统的声辐射问题，将研究对象分为若干个子系统，通过各个子系统之间的能量耦合作用，建立能量平衡方程，然后求解各个子系统的平均振动或噪声水平.图1表示了具有两个子系统的能量传递关系，子系统1、子系统2的输入能量可以表示为

P1=Pdiss1+P12

(1)

P2=Pdiss2+P21

(2)

式中,P1、P2为子系统1，2的输入功率；Pdiss1和Pdiss2为子系统1,2的损耗功率；P12为子系统1到子系统2的传递功率；P21为子系统2到子系统1的传递功率.其中，E1和E2分别为子系统1、子系统2中储存的能量；η1和η2为阻尼损失因子.且

P12=-P21=ωη12E1-ωη21E2

(3)

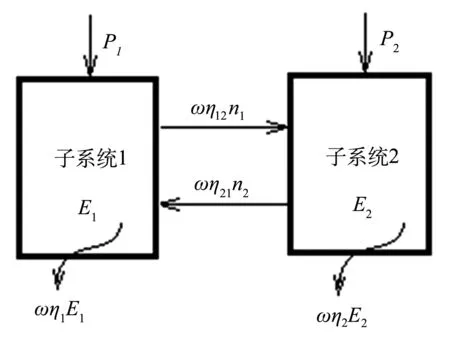
图1 统计能量两个子系统能量递关系

如果系统中存在m个子系统，那么就会产生m个能量平衡方程，其矩阵形式如下

(4)

其中，ω表示分析带宽内的中心频率；ηij表示能量从子系统i传递到子系统j时的耦合损耗因子；ni表示子系统i的模态密度；Ei表示子系统i的能量；Pi表示子系统i时间平均上的输入能量.

式(4)可以简化为:

ω[L][E]=[P]

(5)

其中，[P]为输入能量向量；[L]为关于内损耗因子、耦合损耗因子的矩阵；[E]为子系统的能量向量.

1.2 有限元-统计能量混合分析理论

结构动力有限元方程可以表示为[8- 9]

Dq1=f

(6)

式中,D=-ω2M+iωC+K为结构动力刚度矩阵;M、C、K分别为系统质量、阻尼和刚度矩阵;ω为激励频率;q1为广义位移向量;f为广义载荷.

如果系统中除了用有限单元方程式(6)表示的确定系统外，还存在基于统计分析的不确定性子系统，不确定子系统运动方程可以表示为

(7)

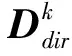
(8)

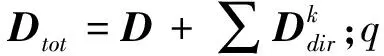
1.3 隔声计算

结构系统在入射声波的作用下产生振动，并将声波传递到结构另一侧，则系统的隔声传递损失表示为

(9)

其中,EI和ER分别为入射声室的声能量和辐射侧声室的声能量，本文在高频段用统计能量法计算得到，中低频段用有限元统计能量混合法计算得到.

2 铝型材有限单元及统计能量分析模型

2.1 铝型材结构截面

动车组车体典型铝型材结构截面如图2所示，铝型材结构包括上板、下板及中间筋板构成，上、下板及筋板中间构成三角形或者梯形的空腔，铝型材各板件厚度及内部腔型对其隔声性能有很大影响.

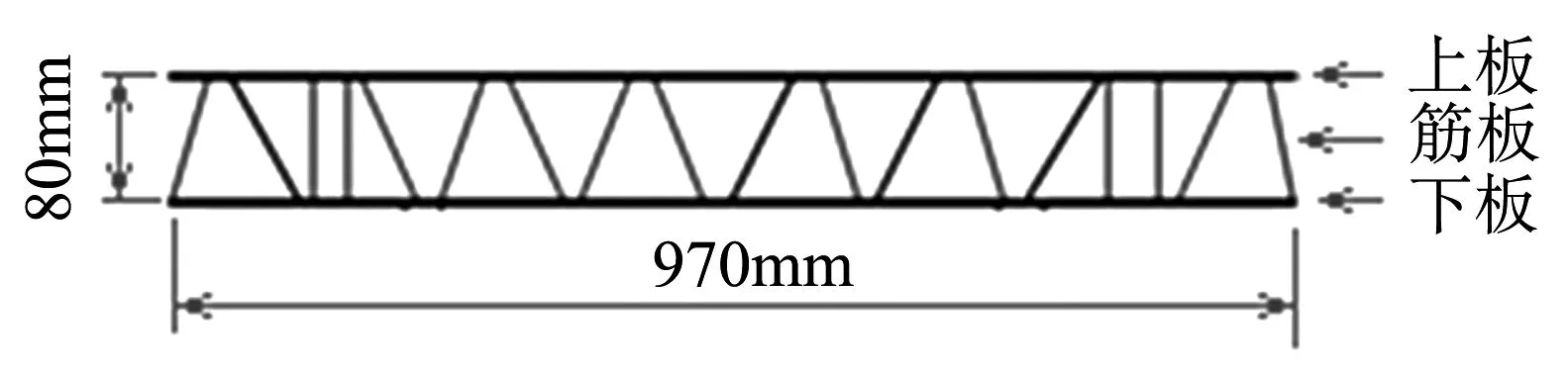
图2 铝型材截面

2.2 铝型材有限单元模型

铝型材有限单元模型如图3所示，将铝型材划分为四边形壳单元，单元尺度20 mm，共划分单元数为23 000.

图3 铝型材有限单元模型

2.3 有限元统计能量混合模型

在铝型材四周的节点上施加固定位移约束，定义材料属性，该有限单元模型即为混合系统中的确定性子系统.在一侧创建混响入射声场，另一侧创建半无限流体，分别用来模拟入射声场和辐射声场，则入射声场和辐射声场即为系统中的不确定子系统.这种基于有限单元统计能量计算铝型材中低频隔声性能的混合模型如图4所示.

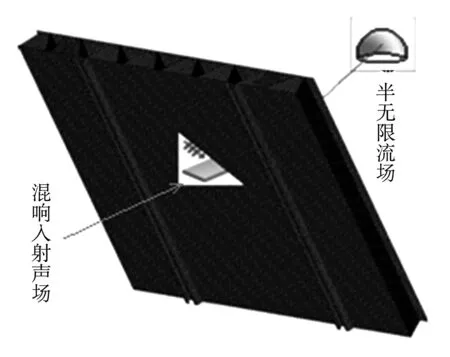
图4 有限元计能量混合模型

2.4 统计能量分析模型

在高频段，用统计能量法进行计算，参考文献[10]中的方法，将图2中的铝型材上板、筋板和下板各划分一个子系统，在铝型材两侧分别建立混响声场子系统，分别用来模拟入射声场和辐射侧声场，用于高频段计算的统计能量分析模型如图5所示.

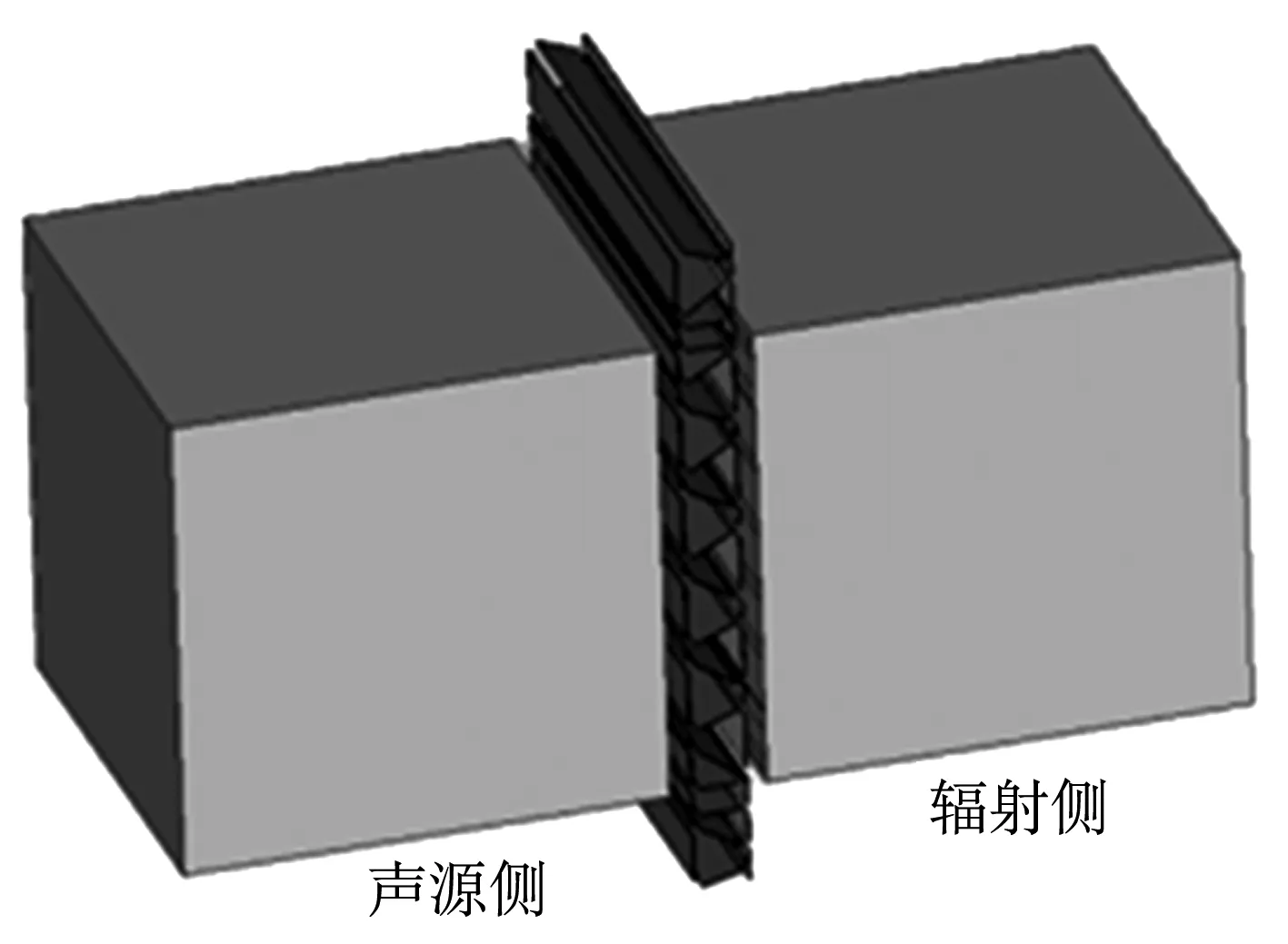
图5 统计能量分析模型

2.5 隔声计算结果

预测的铝型材隔声曲线如图6所示，图6表明该动车组车体大部件铝型材隔声量预测结果为Rw=32.4 dB.隔声曲线在中心频率315 Hz以下的1/3倍频带局部较低.

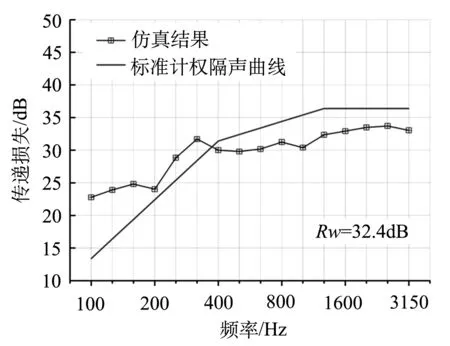
图6 统计能量分析模型

3 铝型材隔声试验

3.1 隔声量测试方法

根据ISO 140-3:1995等相关标准规定，使用混响室-混响室方法测试动车组车体大部件铝型材的隔声量.在发声室使用12面无指向声源输出粉红噪声作为激励，频率范围为中心频率100～3 150 Hz的1/3倍频带.在发声室和受声室内，分别无规则布置6个麦克风，同时测得两个混响室的平均声压级L1和L2.将测试结果代入式(10)，得到试件的频率隔声量R.

(10)

式中,S为试件表面积;T为受声室混响时间;V为受声室容积.

3.2 测试与计算的隔声性能分析

测试的铝型材隔声曲线如图7所示，图7中也给出了仿真计算的隔声曲线，图7表明该铝型材隔声预测结果的频率曲线和试验结果吻合较好，计权隔声量Rw值仅相差0.2 dB.因此，铝型材的隔声预测是有效且准确的.

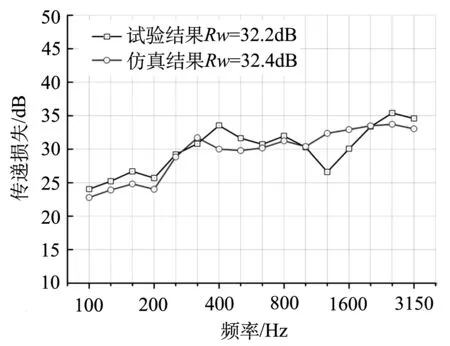
图7 测试及仿真计算的隔声曲线

4 铝型材隔声影响参数分析

4.1 面板、筋板厚度变化对隔声量的影响

图8给出了铝型材下板厚度变化和筋板厚度变化对其隔声性能的影响规律.由图可见，铝型材的隔声量几乎在全频段均随着下板厚度的增加而提高，增加下板厚度对于提高铝型材的隔声具有积极作用.由图可见，铝型材的隔声量在中心频率800 Hz以下的1/3倍频带，基本随着筋板厚度的增加而增加；而在800 Hz以上的1/3倍频带，则基本随着筋板厚度的增加而降低.总体上，铝型材的隔声量随着筋板厚度的增加略有降低趋势.

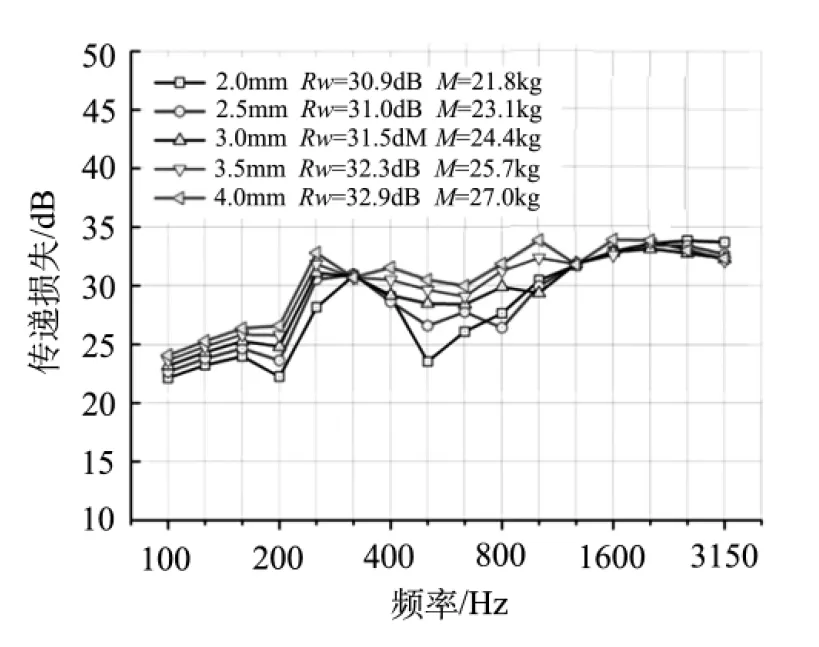
(a) 下板厚度变化对隔声量的影响

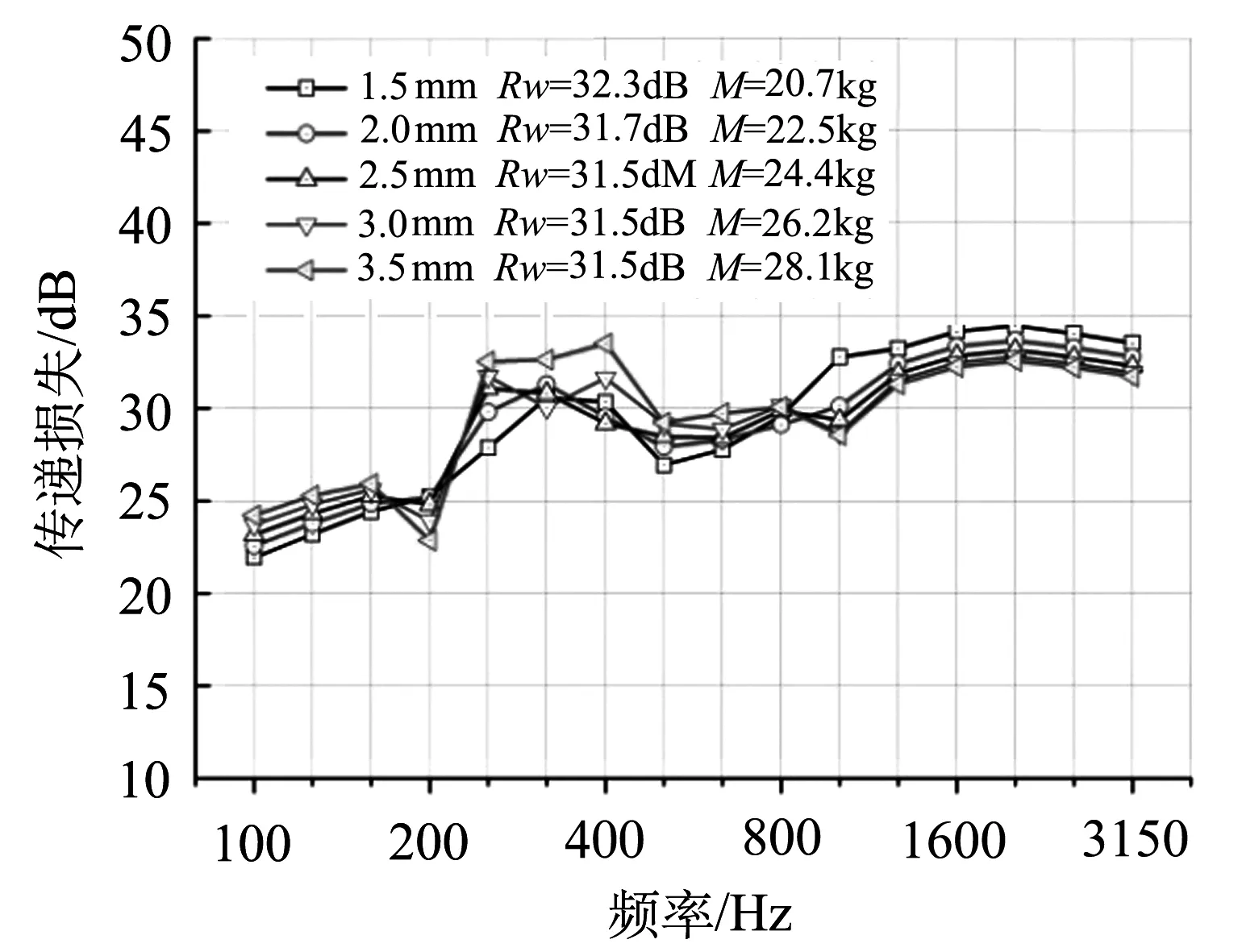
(b) 筋板厚度变化对隔声量的影响

4.2 不同筋板布置形式对隔声量的影响

铝型材主要的筋板型式包括梯形、三角形和矩形三种，如图9所示.由图可见，在中心频率250 Hz以下的1/3倍频带，三角形筋板、梯形筋板、矩形筋板的隔声频率曲线依次降低；在中心频率250～1 000 Hz的1/3倍频带，三角形筋板、矩形筋板的隔声频率曲线明显高于梯形筋板；在中心频率1 000 Hz以上的1/3倍频带，梯形筋板的隔声频率曲线略高于三角形筋板和矩形筋板.

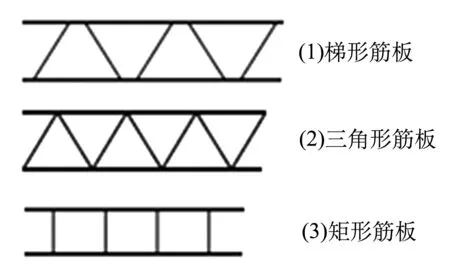
(a) 筋板形式

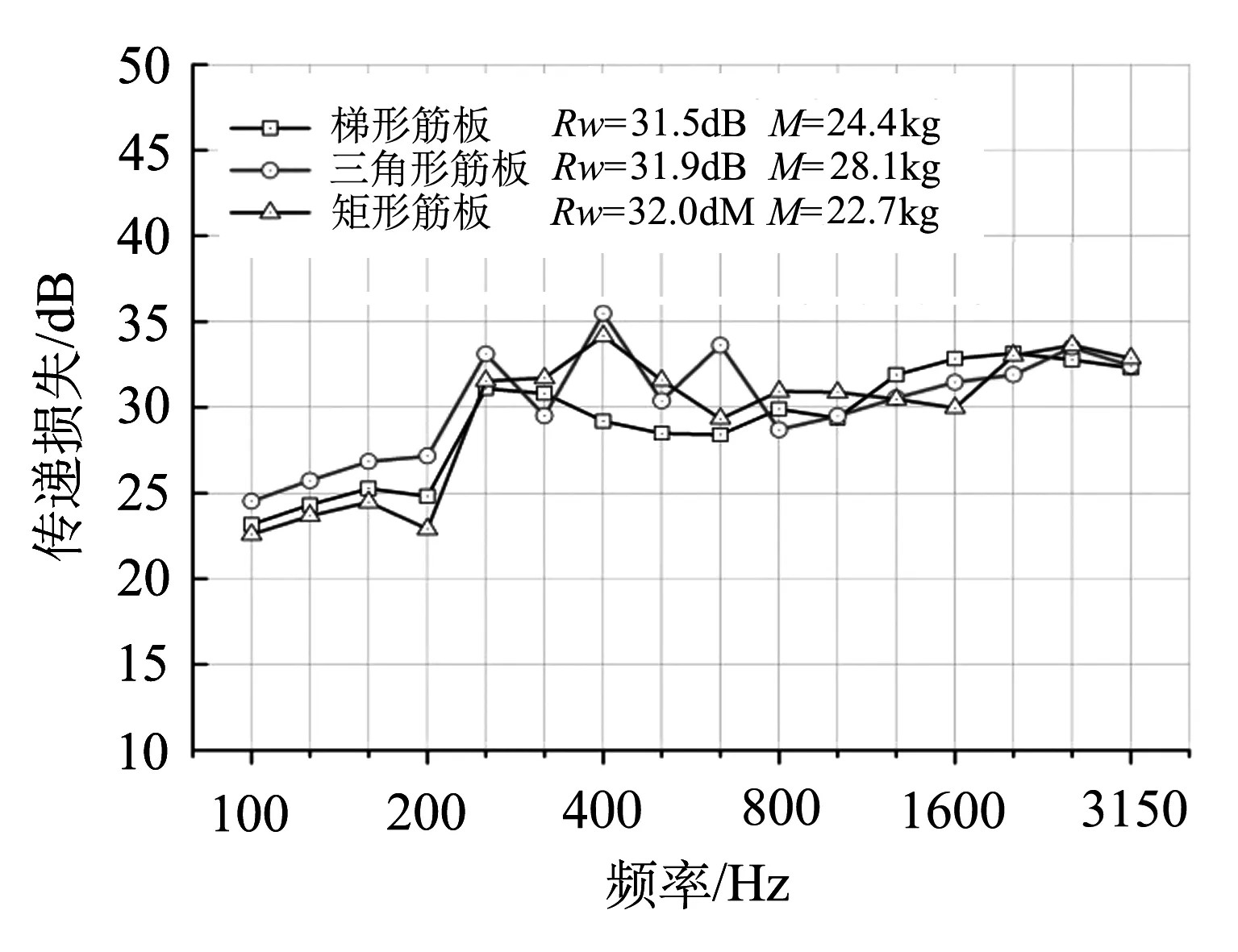
(b) 不同筋板形式隔声曲线

4.3 整体厚度对隔声的影响

铝型材总体厚度是上板和下板之间的距离，如图2所示，初始的铝型材总厚度为80 mm.图10给出了铝型材整体厚度变化对其隔声性能的影响，图10表明，铝型材的隔声量基本上随着高度的增加有提高趋势，在超过300 Hz中高频段，隔声性能随着铝型材总体厚度的增加而增大.

图10 总厚度对隔声性能的影响

5 结论

(1)分频段建立了动车组车体大部件铝型材的隔声仿真模型，在中、低频段采用有限元统计能量混合模型，在高频段采用统计能量分析模型，计算的铝型材隔声曲线与试验结果吻合，计权隔声量误差小于0.2 dB，验证了仿真模型的正确性;

(2)铝型材隔声量随着面板厚度的增加而增加，增加筋板的厚度会使隔声量略有降低;

(3)筋板布置形式在不同的频率段对隔声量的影响不同，在小于800 Hz的低频段，三角形筋板的隔声性能高于梯形筋板和矩形筋板，矩形筋板在低频段隔声性能最差；总体来看，三角形筋板的隔声性能略好于梯形筋板和矩形筋板;

(4)在第一个隔声低谷200 Hz附近，随着铝型材总厚度增加隔声量有所降低，在超过300 Hz中高频段，隔声性能随着铝型材总体厚度的增加而增大，可以看出增加铝型材总厚度有利于控制高频噪声.

[1]张卫华.高速列车顶层设计指标研究[J].铁道学报,2012,34(9):15- 19.

[2]沈艳详，宋雷鸣.动车组车内噪声设计理念研究[J].噪声与振动控制，2010(1):33- 35.

[3]陈燕荣,肖友刚,朱晓燕.动车组用铝合金型材隔声系能优化[J].铁道车辆,2016,54(12):11- 15.

[4]张媛媛,沈火明,肖新标.高速列车铝型材外地板结构振动与隔声量分析[J].重庆理工大学学报,2014,28(1):28- 32.

[5]王瑞乾.高速列车地板结构隔声及隔声提高方法探究[D].成都：西南交通大学，2014.

[6]丁政印.高速列车车体板件声学性能分析及数据库的建立[D].杭州：浙江大学，2015.

[7]周新祥. 噪声控制技术及其新进展[M]. 北京：冶金工业出版社，2007.

[8]杨雄伟,李跃明,耿谦.基于混合FE-SEA法的高温环境飞行器宽频声振特性分析[J].航空学报，2011,32(10):1851- 1859.

[9]SHORTER P J,LANGLEY R S.On the reciprocity relationship between direct field radiation and diffuse reverberant loading[J].Journal of the Acoustical Society of Amrica,2005,117(1):85- 95.

[10]XIE G,THOMPSONB D J,JONES C J C.A modeling approach for the vibroacoustic behaviour of aluminium extrusions used in railway vehicles[J].Journal of Sound and Vibration,2006,293:921- 932.