船舶电缆老化预测研究
吕志立,,
(1.厦门三安集成电路有限公司,福建 厦门 361021;2.集美大学轮机工程学院,福建 厦门 361021)
0 引言
船舶电缆承担整艘船舶电能的传输,是船舶组成中非常重要的角色。海上湿度较大,盐度较高,机舱油雾浓度高,并且电缆线芯在电能和电信号的传输过程中会产生相当大的热量,以及电缆受到不同程度的振动和冲击等,在众多因素的综合作用下电缆绝缘层材料很容易受到损坏,导致绝缘性能下降甚至失效,进而影响船上电气系统的安全和稳定,轻则船舶无法正常运行,重则船毁人亡。船舶电缆与陆上电缆有显著不同,陆上电缆是通过高架线路进行铺设的,而船舶电缆通过电缆托架进行铺设,电缆与电缆托架之间会构成电容器,在海洋环境下,电缆绝缘层易被腐蚀老化,同时伴有短路电弧。目前,关于电缆故障诊断的研究主要针对寿命预测[1-3]和故障位置定位[4-10],然而针对电缆老化预测方面的研究较少[11]。因此,本文提出一种基于卡尔曼滤波器的船舶电缆老化预测方法。
1 船舶电缆老化过程中阻抗和电弧电流有效值变化规律
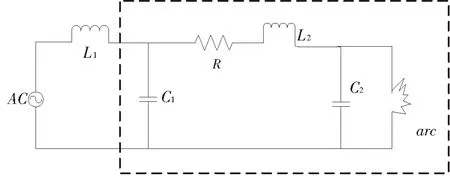
图1 船舶电缆模型Fig.1 The Model of Ship Cable
1.1 船舶电缆老化过程
船舶电缆是均匀传输线路,船舶电缆模型如图1所示。其中:电感L2表示每单位长度电缆具有的电感;R表示每单位长度电缆具有的电阻;C2表示每单位长度电缆具有的电容;C1表示由于电缆老化使电缆与电缆托架之间构成电容器的电容;arc为电缆老化过程中产生的短路电弧;AC是交流电源;L1集中反映交流电流在通过除老化电缆之外的其余电缆线时产生的磁场效应[12]。
电缆老化表现为:绝缘层逐渐被腐蚀,绝缘性越来越差,C1的电介质相对介电常数εr变小,根据C=εrS/(4πkd)(其中:C表示电容量;εr表示相对介电常数;S表示电容器两极板正对面积;d表示两极板的距离;k表示静电常数;π表示圆周率。)可知,C1的电容值也会逐渐变小;当电缆的绝缘层被腐蚀处于临界状态时,C2两端将会产生短路电弧,并且随着绝缘性越来越差,短路电弧的电导率Gs0将逐渐增大。
1.2 阻抗和电弧电流有效值变化规律
图1中电缆模型的阻抗公式为:
Z=(R+jωL2+Zx)(-j(1/(ωC1)))/(R+jωL2+Zx-j(1/(ωC1))。
式中:Z表示船舶电缆的阻抗,C2和短路电弧并联的阻抗Zx=Zarc(-j(1/(ωC2)))/(Zarc-j(1/(ωC2))),Zarc表示短路电弧的阻抗;ω为角频率。
船舶电缆与船舶机舱及机舱的其他电气设备是相互绝缘的,在电缆老化过程中会出现短路电弧,电弧是一种气体导电现象,由于电弧的产生使船舶电缆与船舶机舱及机舱的其他电气设备通过电弧构成回路,产生电弧电流,即短路电流,导致电力系统局部短路,随着电缆老化越来越严重,电弧电导率逐渐变大,产生的电弧电流也会越来越大。电弧电流越大,电力系统局部短路的短路电流也会越大,船舶电力系统的安全性和稳定性也就越差,因此可以用电弧电流的变化反应船舶电力系统的安全性和稳定性。

1.3 阻抗和电弧电流有效值数据采集
在仿真实验中首先搭建船舶电缆模型,通过减小模型中电缆与电缆托架构成的电容器的值,增大短路电弧电导的值,模拟电缆的老化过程,采集电缆老化过程中阻抗值和电弧电流有效值,并且观察它们的变化规律。
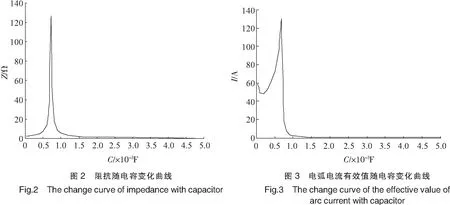
在电缆老化过程中,电容C1逐渐减小,仿真实验中C1的变化范围是5×10-3~2×10-5F[12],阻抗的变化规律如图2所示。由图2可知,在电缆老化过程处于临界时阻抗会发生突变。
在电缆阻抗突变之前,电弧的导电率Gs0几乎不变,仿真实验中Gs0=0.2 S。当电缆阻抗突变之后,电弧的电导率按线性关系增加,仿真试验中电容C1每增加0.0001 F,相应地电导也增加15 S。电弧电流有效值随电容变化的关系如图3所示。由仿真结果可以表明,电缆在老化过程中会产生短路电弧,同时电弧电流有效值会突变,并且之后一直会保持很大的值。
2 基于卡尔曼滤波算法的船舶电缆老化预测方法
2.1 船舶电缆老化预测原理
本文所提出的预测方法是利用卡尔曼滤波算法对电缆老化过程中的阻抗值进行预测,用预测到下一个状态的阻抗值和当前状态阻抗值的残差Wn来表示阻抗的突变,通过残差检测电缆老化产生前期故障的临界状态。
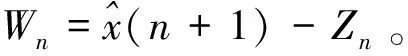
阻抗残差的临界值为H1n,如果Wn>H1n,表明电缆老化产生了前期故障。
电弧电流有效值In的临界状态为H2n,如果电弧电流有效值In>H2n,表明电缆的老化使船舶电力系统的安全性和稳定性受到威胁,需要及时更换电缆。
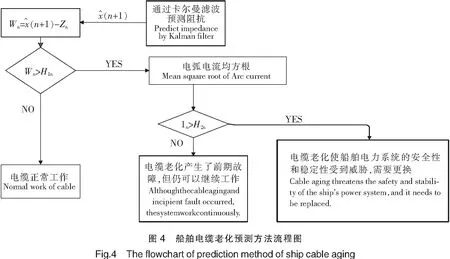
基于此原理,本文提出的船舶电缆老化预测方法流程图如图4所示。
2.2 卡尔曼滤波算法的推导
2.2.1 船舶电缆阻抗动态模型
船舶电缆阻抗离散时间的动态系统由描述状态向量的状态方程和描述观测向量的观测方程共同表示。
1)状态方程
x(n+1)=F(n+1,n)x(n)+G(n+1,n)U(n)+v1(n)。
(1)
式中:M维向量x(n)表示船舶电缆阻抗在离散时间n的状态向量;M×M矩阵F(n+1,n)描述船舶电缆阻抗在时间n的状态到n+1的状态之间的转移过程;M维向量G(n+1,n)描述船舶电缆阻抗在时间n的状态到n+1的状态之间受其他因素的影响;U(n)代表新息;M维向量v1(n)描述研究船舶电缆阻抗过程中因简化或忽略一些因素而产生的误差,假设v1(n)是均值为零的白噪声序列,因此它的最优估计为零。
图1所描述的船舶电缆模型中,电容C1在老化过程中会随着时间逐渐变化,用C1(n-1)和C1n表示C1变化过程中n-1和n两个时刻的状态,n-1时刻电缆模型的阻抗值可由式(2)表示。
Zn-1=(R+jωL2+Zx)(-j(1/(ωC1(n-1))))/(R+jωL2+Zx-j(1/(ωC1(n-1))))。
(2)
在Zn的表达式中,令C1n=C1(n-1)+ΔC,则
Zn= (R+jωL2+Zx)(-j(1/ω(C1(n-1)+ΔC)))/
(R+jωL2+Zx-j(1/(ω(C1(n-1)+ΔC))))。
(3)
把式(2)化简为
Zn=Zn-1+ωΔCj。
(4)
构建船舶电缆阻抗的状态方程,需要把式(4)转换为如式(1)一样的向量形式,动态方程(4)可以改写为
xn=Fxn-1+GU。
(5)
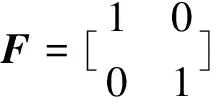
2)观测方程
y(n)=H(n)x(n)+v2(n)。
(6)
式中:N维向量y(n)描述船舶电缆阻抗在时间n的观测向量;N×M矩阵H(n)描述船舶电缆阻抗在离散时间n的状态向量和观测向量之间的关系;N维向量v2(n)描述船舶电缆阻抗在测量过程中存在的误差,假设v2(n)是均值为零的白噪声序列,因此它的最优估计为零。
对于解决这个问题的优化算法,主要有H∞滤波算法和卡尔曼滤波算法[13-15],而可以证明卡尔曼滤波算法比H∞滤波算法在跟踪不平稳系统时具有更优的性能,所以本文利用卡尔曼滤波算法的思想来预测Zn。
鉴于本文的研究重点,对它们之间性能的比较本文不再赘述。
2.2.2 船舶电缆阻抗预测

由观测方程(6)可知,在n+1时刻电缆阻抗观测值y(n+1)的估计值为:
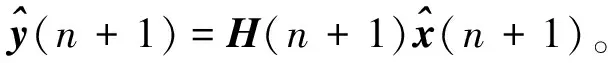
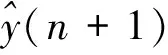
卡尔曼系数用来权衡阻抗预测模型和阻抗观测模型的比重,用其构建船舶电缆阻抗的预测公式,更新公式如下:
(7)


(8)
其中:Pt(n)是状态协方差矩阵;F是状态转移矩阵;Q是状态转移协方差矩阵。
每一轮迭代后状态协方差矩阵需要不断更新,以便下一轮迭代时使用,状态协方差矩阵的更新方程为:
2.2.3 卡尔曼滤波算法总结
船舶电缆阻抗的动态方程为:
(9)
应用卡尔曼滤波算法对船舶电缆阻抗进行预测:
1)电缆阻抗和状态协方差矩阵的预测:
(10)
(11)
2)卡尔曼系数的计算:
HT(n+1)+R(n+1)]-1。
(12)
3)电缆阻抗和状态协方差矩阵的状态更新:
(13)
(14)
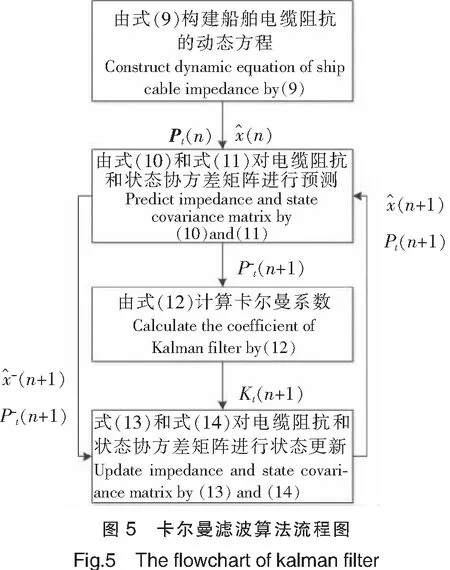
为了便于分析,基于卡尔曼滤波算法的电缆阻抗预测流程如图5所示。
3 船舶电缆老化预测方法仿真实验
仿真实验对上述推导的船舶电缆老化预测方法进行模拟,仿真参数如下:
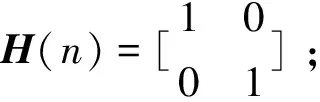
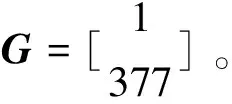
图6为通过卡尔曼滤波算法预测到阻抗值的估计值;图7为阻抗的残差信号Wn;图8为阻抗的残差信号Wn与电弧电流In的比较。
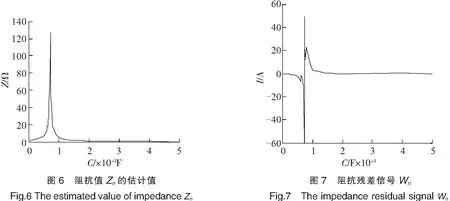
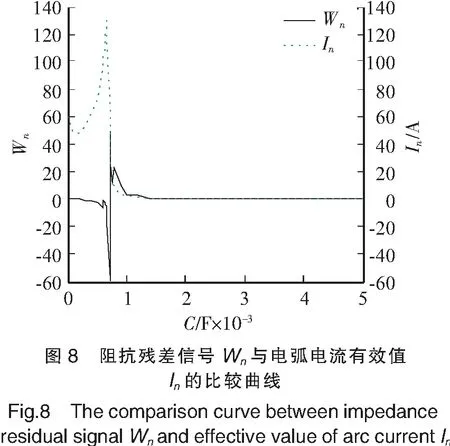
图7中Wn开始增大时,表明预测到的下一个状态的阻抗值与当前状态的阻抗值存在很大差异,即Zn开始发生突变;很显然,在临界处Wn>H1n,由此可知电缆已进入非正常工作状态。另外,由于电弧的产生使船舶电缆与船舶机舱及机舱的其他电气设备通过电弧构成回路产生电弧电流,即短路电流,导致电力系统局部短路。图8中Wn开始增大之后,电弧电流有效值In也迅速增大,并且之后保持很大,表明电力系统局部短路的短路电流也会迅速增大,并且之后保持很大。当电弧电流有效值大于临界状态时,电力系统局部短路的短路电流会威胁船舶电力系统的安全性和稳定性,此时需要及时更换电缆。
仿真结果表明该方法可以对船舶电缆老化状况进行预测。
4 结论
针对船舶电缆老化预测,本文首先建立船舶电缆的老化过程的模型,得出阻抗和电弧电流的变化规律,然后利用卡尔曼滤波算法对电缆老化过程中的阻抗值进行估计,进而得到实际值和估计值之间的残差,通过预测的阻抗值和当前阻抗值的残差来检测电缆工作状态,利用电弧电流的突变特性预测船舶电缆老化产生前期故障的临界状态。最后,通过仿真实验验证了该方法是可行的。
[1]魏一.船用低压电缆剩余寿命预测理论与实验研究[D].大连:大连海事大学,2012.
[2]高云鹏,谭甜源,刘开培,等.电缆接头温度反演及故障诊断研究[J].高电压技术,2016,42(2):535-542.
[3]杨春宇.电力电缆故障分析与诊断技术的研究[D].大连:大连理工大学,2013.
[4]牛睿.输电线路故障定位研究及其分析平台开发[D].济南:山东大学,2015.
[5]刘亚东.输电线路分布式故障测距理论与关键技术研究[D].上海:上海交通大学,2012.
[6]彭浩,沈兴来,陈奎.电缆单端故障测距的阻抗-行波组合法[J].电力系统保护与控制,2016,44(23):110-114.
[7]伏圣群.行波反射法电缆故障检测关键技术研究[D].哈尔滨:哈尔滨理工大学,2014.
[8]张建国,徐航,马荔,等.面向电缆故障检测的布尔混沌时域反射法[J].工矿自动化,2016,42(1):35-39.
[9]吕志立.船舶电力系统故障演化机理与预测方法研究[D].厦门:集美大学,2017.
[10]姚海燕,张静,留毅,等.基于多尺度小波判据和时频特征关联的电缆早期故障检测和识别方法[J].电力系统保护与控制,2015(9):115-123.
[11]许奇歆,王荣杰,周海峰.电力系统故障预测方法研究[J].电工摘要,2016,12(6):6-11.
[12]GHANBARI T.Kalman filter based incipient fault detection method for underground cables[J].IET Generation Transmission & Distribution,2015,9(14):1988-1997.
[13]LV Q,ZHANG X D YING J.Kalman filtering algorithm for blind source separation[C].Philadephia:ICASSP 2005,2005.
[14]ZHU X L,ZHANG X D,YING J.A new kalman filtering algorithm for nonlinear principal component analysis[J].Springer Berlin Heidelbers,2005,3496:1010-1015.
[15]NIVA D,AUROBINDA R,PRADIPTA K D.A robust H infinite learning approach to blind separation slowly time-varying mixture of acoustic electronmechanical signals[J].Mechanical Systems and Signal Processing,2009,23(6):2049-2058.

