基于风险偏好调权的三参数区间数型多指标群体决策方法
宋之杰,王浩,赵红美
(燕山大学经济管理学院,河北秦皇岛066004)
0 引言
针对多指标决策问题,多维指标和各决策者权重的确定十分关键,关于该方面的研究成果较多,大致可总结为主观赋权和客观赋权两类。主观赋权来自于决策者丰富的知识与经验,Delphi法和AHP法最为成熟和常用,但赋权结果的主观随性较大。而群决策问题中追求原始评价数据确定客观赋权更加具备数理依据。Wei[1]考虑评价值离差的最大化求解各指标权重大小,然后通过加权平均算子获得综合评价值。Li等[2]基于群体不一致最小思想,建立多目标约束模型获得指标权重。Yue[3,4]通过确定理想方案,基于TOPSIS与投影法对决策者权重进行计算和调整后进行决策信息的集中。这类确定权重的方法可能过度依赖客观信息而忽视主观决策者意愿,出现与现实指标重要度不符的情形。对此,主客观相结合的综合赋权方法则在一定程度上有所改进。周荣喜等[5]依据客观数据稳定性与属性权重的正相关关系,由熵值确定属性客观权重,提出了基于偏好系数获得指标综合权重的方法。Rao等[6]通过评价值方差确定的指标客观权重与主观赋权,以不同比重重新进行集结而求解得综合权重。Almeide等[7]考虑决策者的偏好信息,在群体决策过程中提出一种灵活互动的权重衡量方法,以改善传统的折衷调整方法。上述方法均是涉及指标权重,很少在同一标准下同时考虑各决策者权重的确定。决策者风险偏好在主观赋权过程中是不可忽略的主观意愿,而客观赋权下考虑决策者风险偏好对多指标群体决策者多阶段权重的共同影响,还有待研究。
针对决策信息难以用确定数描述的多指标决策问题,区间数受到较大关注[8,9]。但是区间数在描述决策信息时存在一些不足:其一,区间取值一般表现为均匀分布;其二,为涵盖取值范围而使区间变大,运算后的结果可能导致信息失真。为此,三参数区间数开始得到广泛运用。Lan等[10]在决策过程中结合模糊集定义了三参数区间数模糊值运算规则和距离测度。Luo等[11]基于灰色理论,提出了一种考虑主客观权重的三参数区间数的多属性灰靶决策方法。闫书丽等[12]基于前景理论下利用“奖优惩劣”的三参数区间数变换,依据综合前景值进行排序。在三区间参数现有的应用研究中,重心值在排序结果中体现出特殊性的较少,风险偏好分析中熵测度用于三区间参数型的多指标群决策问题的文献不多。
鉴于此,对于多指标评价值为三参数区间数的群体决策问题,本文针对重心值的特殊属性,定义一种简化的距离公式和记分函数排序法,基于信息熵理论,以及决策过程中群体意见偏差最小与差异性保留的偏好关系,提出了一种同时考虑决策风险偏好确定的决策指标与各决策者权重的方法,补充三参数区间数型多指标群体决策的理论方法,从多角度为相关部门的群体决策问题提供客观和科学的决策参考。
1 三参数区间数的相关定义
在实际决策情形中,当决策者认为区间数参量有一个最可能值时,区间数不能更好地描述决策信息。因此,本文在区间数基础上提出三参数区间数,使得决策评判过程更加符合实际,其定义如下:
定义1[13]:设区间数[al,au]是一个包含最大可能性取值为aˉ的区间数,则称a=[al,,au]为三参数区间数。
定义1中,al和au为三参数区间数的上界和下界,为其重心,al<ˉ<au,区间长度表示为la=au-al。当al=或=au时,三参数区间数退化为区间数;当al=ˉ=au时,三参数区间数退化为实数。三参数区间数在同等标度下满足一些基本运算法则和性质,见文献[13]。

定义2:设a=[al,,au]与b=[bl,ˉ,bu],二者的距离为:相比文献[13]和文献[12]中的定义,d()a,b考虑到重心的特殊性,简化并赋予了三参数区间数的上下界与重心不同的权重系数。其中,ε1和ε2为决策者对区间数左右端点的偏好系数,ε1+ε2=1。本文认为决策者偏好于取值越大越好,故假设ε1取值0.7,ε2取值0.3。特别地,当,未知时,距离公式退化为求解区间数距离,即当a=b时,d()a,b=0。
定义3提出的三参数区间数的记分函数排序考虑了三参数区间数的重心与端点对其排序的影响。文献[12]定义的可能度其中,m(a)和m(b)分别是三参数区间数a和b的中点,可证明与p(a>b)是等价关系。相比于可能度的排序方法,该定义的记分函数排序计算简单,最显著的特点是通过记分函数差值,能够定量和直观地判断三参数区间数a对b的优劣程度。
2 考虑风险偏好调整权重的决策方法
2.1 问题的描述
设某一多指标群体决策问题,其方案集S={s1,s2,…,sm},i=1,2,…,m;评价指标集C={c1,c2,…,cn},j=1,2,…,n;决策者构成的决策集D={d1,d2,…,dp},k=1,2,…,p;决策者dk对于方案si下指标cj的评价值形成的矩阵,其中依据决策者经验与组成结构,对指标给出的主观赋权向量下文将依据以上信息进行方案的排序。
2.2 决策方法和步骤
步骤1:指标评价值的规范化处理
为消除不同指标下准则信息在量纲上的差异性,增加其可比性,本文采用三参数区间数的极差变换公式[11]。
针对收益型指标:
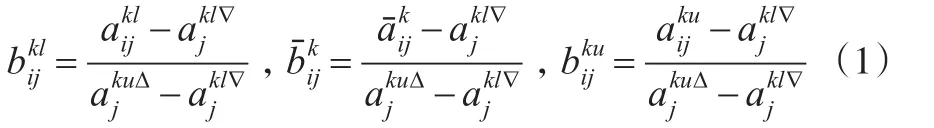
针对成本型指标:

步骤2:熵测度下指标风险偏好调整权重
在信息熵理论中,信息熵越小,那么在指标信息中的差异性越大,其提供的信息量越多,综合决策中的影响越显著[14]。本文考虑三参数区间数重心的特色性质,以区间数长度和重心为参数,通过熵测度来衡量指标评价值的差异程度。


关于三参数区间数信息下指标评价值的权重熵测度为:
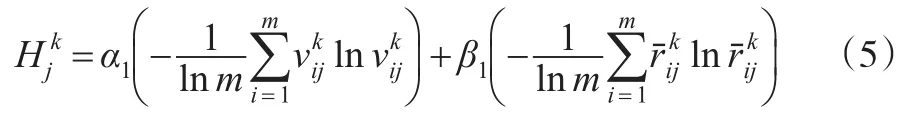
在式(5)中,α1和β1分别为三参数区间数长度和重心的偏好系数,且α1+β1=1。当α1>β1时,决策者偏好于指标评价值的上下限范围,则认为其是风险追求者;当α1<β1时,决策者偏好于指标评价值的最可能值,则认为其是风险规避者;当α1=β1时,则认为决策者是风险中立者。由此,定义熵测度的指标综合权重为:
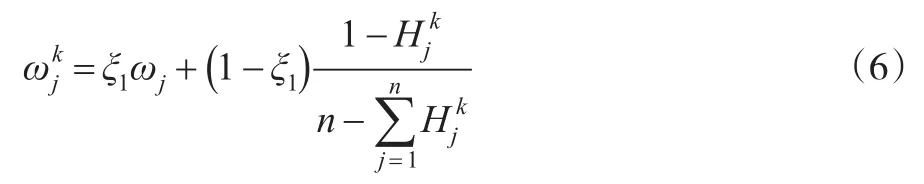
在式(6)中,ξ1表示决策者对指标评价值权重中主客观信息的重视程度。当ξ1>0.5时,决策者较重视指标已赋值主观权重的影响;当ξ1<0.5时,决策者较重视指标评价值客观权重的影响;当ξ1=0.5时,则决策者认为二者同等重要。
步骤3:群体偏差与差异性最小化的风险偏好决策者权重
在步骤2基础上,决策者dk对于方案si下指标cj的评价值信息进行集结,可得出综合指标值为:

式(7)可理解为决策者层面决策者dk对于方案si的综合指标值矩阵为定义uk′是决策者dk的理想综合指标值的决策方案,则由uk′构成的向量称之为群体理想决策集,其中:

针对集结各决策者指标评价值信息的综合指标值,在群体层面下群体意见一致性和偏差最小化极为重要。基于式(7)和式(8),则群体决策在方案si下与群体理想决策的偏差为,那么群体决策下的综合偏差为,则可构建群体意见偏差最小化的优化模型:
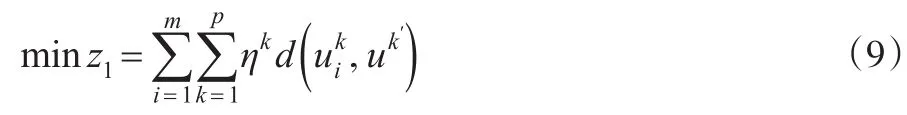
群体决策需要保留个别专家有差异性的意见,过于追求群体偏差最小化反而会导致关键意见和信息的忽略,因此,引入熵测度[14]信息的不确定性极为合适,可构建极大熵的优化模型:

因此,权衡考虑群体偏差与特例保留的双目标,将上述两个优化模型进行等价转化成单目标优化模型M:

步骤4:方案的排序,集结各决策者的综合信息,对于方案si的群体决策综合值为最后依据定义3进行排序。
3 算例分析
本文针对商用大型飞机某零部件的国际供应商的决策问题,由4家供应商构成备选方案集考虑4个指标评价:质量c1、价格c2、设计方案c3以及竞争力c4,集结3位决策者共同决策。依据公司自身因素和历史数据,现对4个评价指标给出主观赋权向量为ω={0.3,0.26,0.23,0.21},指标评价矩阵见文献[12]。
假定决策群体的风险偏好表现为风险追求者类型,则取αq=0.7,βq=0.3,q=1,2。下面依据上述信息结合上文的决策方法,确定最佳方案:
(1)利用式(1)对指标评价矩阵规范化处理,仅价格为成本型指标,结果如下:

(2)依据式(5)和式(6)计算决策者对各指标评价信息熵测度权重。假设对主客观信息保持中立,则式(6)取ξ1=0.5(注:已将ξ改为ξ1),可计算出各决策者下各指标层的综合权重(见表1中风险追求者下的权重值)。
(3)计算各决策者的权重。依据式(7)和式(8),可求得理想决策集为运用MATLAB软件可计算得决策层的权重为ηk=(0.329,0.365,0.306)。(注:已将ηk改为ηk)
(4)方案的排序。计算方案si的群体决策综合值μi为:

为了分析不同风险偏好对决策排序的影响,对比决策群体风险偏好表现为风险追求者和风险规避者(取αq=0.3,βq=0.7,q=1,2)两种决策情形,其计算结果如下页表1所示:
由表1可知,案例中决策者的风险偏好对方案排序结果有较大影响。在风险追求偏好下,本文排序选择最佳方案为s1。在风险规避偏好下,各决策者下指标权重和决策者权重发生相应的变化,与风险追求偏好类型以及文献[12]中考虑期望灰靶决策下的权重相差较大,最终导致排序结果的改变,但是最佳方案s3和次佳方案s1记分函数差值较为接近。对比表中数据可知,风险追求偏好下的排序结果,相邻方案的记分函数值差异相对比较分散,体现出一定的区分度。此外,上述排序结果比可能度排序更加直观地体现出方案之间的优劣程度。

表1 不同风险偏好下各决策者指标权重、决策者权重及排序结果
4 结束语
本文考虑指标值为三参数区间数形式的群体决策问题,通过突显重心值的特殊属性,以及决策过程中群体意见偏差最小与差异性保留的偏好关系,引入熵测度方法,基于风险偏好视角同时对指标阶段和决策者阶段进行权重调整,最终以三参数区间数形式表现各方案的决策综合值,保留了原始的信息含量。该方法注重三参数区间数重心值的意义,提出了一种简化的三参数区间数的距离公式和记分函数排序法,直观地体现了方案间的优劣程度;在确定指标权重阶段和决策者权重阶段考虑了风险偏好的影响,更加符合实际决策情形。最后通过案例分析,在群体决策过程中的风险偏好诉求对不同决策阶段的权重有较大影响,可能导致方案排序结果与其优劣程度发生变化。在后续研究中,如何综合考虑决策者心理行为和风险偏好共同影响,以及在动态环境下构建相应的三参数区间数型群体决策模型,具有一定研究意义。
[1]Wei G W.Grey Relation Analysis Method for 2-tuple Linguistic Multiple Attribute Group Decision Making With Incomplete Weight Information[J].Expert Systems With Application,2011,38(5)
[2]Li D F,Chen G H,Huang Z G.Linear Propramming Method for Mutiattribute Group Decision Making Using If Sets[J].Information Sciences,2010,180(9).
[3]Yue Z L.An Extended TOPSIS for Determining Weights of Decision Makers With Interval Numbers[J].Knowledge-based Systems,2011,24(1).
[4]Yue Z L.Approach to Group Decision Making Based on Determining the Weights of Experts by Using Projection Method[J].Applied Mathematical Modelling,2012,36(7).
[5]周荣喜,范福云,何大义,邱菀华.多属性群决策中基于数据稳定性与主观偏好的综合熵权法[J].控制与决策,2012,27(7).
[6]Rao R V,Pate B K.A Subjective and Objective Integrated Multiple Attribute Decision Making Method for Material Selection[J].Materials and Design,2010,31(10).
[7]De Almeida A T,et al.A New Method for Elicitation of Criteria Weights in Additive Models:Flexible and Interactive Tradeoff[J].European Journal of Operational Research,2016,(250).
[8]Wu X M,Perloff J M.GMM Estimation of a Maximum Entropy Distribution With Interval Date[J].Journal of Economics,2007,38(2).
[9]梁燕华,郭鹏,朱煜明,赵静.基于区间数的多时点多属性灰靶决策模型[J].控制与决策,2012,27(10).
[10]Lan R,Fan J L.TOPSIS Decision-making Method for Three Parameter Interval-valued Fuzzy Sets[J].Systems Engineering-Theory&Practice,2009,29(5).
[11]Luo D,Wang X.The Multi-attribute Grey Target Decision Method for Attribute Value Within Three-parameter Interval Grey Number[J].Applied Mathematical Modelling,2012,36(5).
[12]闫书丽.灰靶决策方法及应用研究[D].南京:南京航空航天大学博士论文,2014.
[13]胡启洲,于莉,张爱萍.基于三元区间数的多指标决策方法[J].系统管理学报,2010,19(1).
[14]邱菀华.管理决策熵学及其应用[M].北京:中国电力出版社,2014.
[15]Winston W L.Operations Research Application and Algorithms[M].Beijing:Tsinghua University Press,2006.

