地铁区间隧道风速监测点选取分析研究

王方宇 毕海权 王宏林 曹 松



地铁区间隧道风速监测点选取分析研究

王方宇 毕海权 王宏林 曹 松

（西南交通大学机械工程学院 成都 610031）

为了确定地铁区间隧道内的平均风速，合理布置风速监测点是准确监测断面平均风速的关键。针对圆形地铁区间隧道，对隧道内活塞风速大小和断面上风速分布进行了数值研究，研究结果表明区间隧道内的活塞风速大小为2m/s～10m/s；通过将监测点布置在平均风速点处直接测得隧道平均风速的方法是不可行的，而通过修正监测点风速得到隧道内的平均风速的监测方法是可行的，并给出了隧道断面上不同监测点处风速与断面平均风速的计算公式；隧道内监测点风速与隧道平均风速呈线性关系，且监测点离隧道中心越近，线性关系的相关性越高。

地铁区间隧道；风速监测点；平均风速；风速分布；数值计算

0 前言

地铁隧道内的风速大小和分布是决定隧道内是否拥有一个良好环境的重要因素[1]，为保证隧道内合理的风环境，有必要对地铁隧道内风速进行长期监测。由于隧道环境十分复杂，风速监测点位置的选取是准确监测风速的关键，监测点的选取原则包括两方面，一是该位置点处的风速能够直接或者间接反应出隧道平均风速，二是监测处布置的传感器不能越过车辆限界，避免其对行车安全造成影响。

现有对于列车活塞风的研究主要集中在活塞风特性、活塞风的影响因素以及隧道内通风方案的优化[2-6]，对隧道断面上风速分布规律的研究很少。国内外关于地铁隧道风速的监测点选取的研究几乎空白，仅有对地铁活塞风测试的相关研究。以往研究人员在进行地铁隧道风速测试时，常用的测试方法是在隧道两侧布置若干个测点，或采用人工手持测试的办法在多个位置进行测试。但由于实际隧道内的风速并不均匀，上述多点布置的方法不仅会大大增加监测系统建设成本，而且还会增加测试仪器安装和维护的难度，因此目前隧道风速测点的选取方法并不合理，不能直接用于风速监测。本文采用数值计算方法分析了区间隧道的活塞风速大小变化范围和断面上风速分布特性，并研究了圆形区间隧道断面上风速监测点选取方法的可行性。

1 数值计算方法

1.1 计算模型

本文重点研究圆形盾构地铁区间隧道，计算模型参照重庆某轨道交通线区间隧道，并对隧道内部管线等凸起结构进行了适当简化，如图1、图2所示。

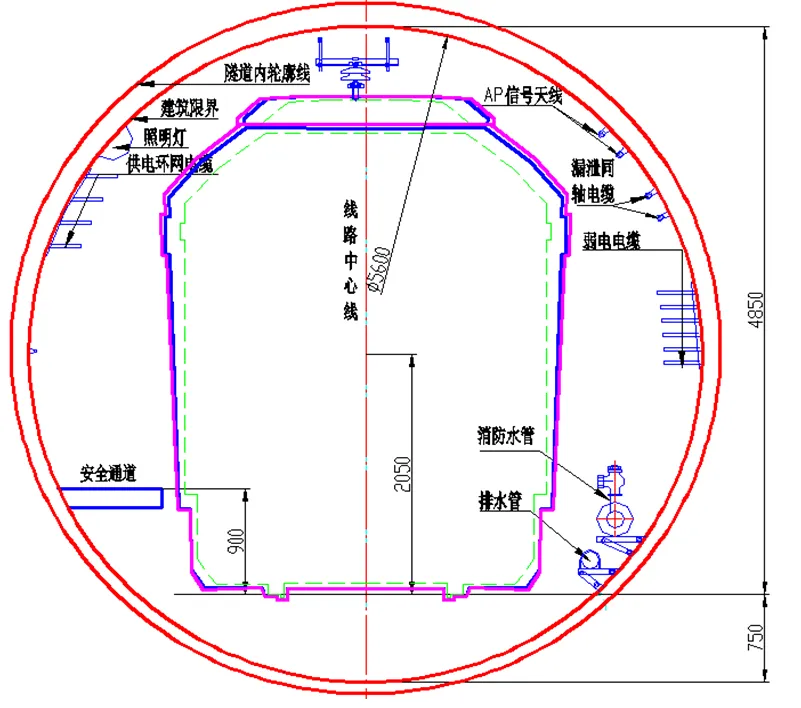
图1 区间隧道内部结构示意图

图2 区间隧道计算模型

数值计算中隧道长度为500m，圆形区间隧道的断面直径分别为5.2m、5.4m、5.6m、5.8m、6.0m。

计算模型采用多面体网格进行划分，五种尺寸隧道模型的网格单元数量约为690万～970万。

1.2 边界条件和求解条件

隧道模型包括一个风流入口和一个风流出口，风流入口设置为速度入口，风流出口设置为压力出口，隧道壁面设置为固定壁面。隧道壁面的衬砌粗糙高度取0.0089m，轨面的粗糙高度取0.0095m。

计算中假定隧道壁面与空气无热交换，且隧道内无质量源输入，隧道内的空气流动视为粘性不可压缩流动。模拟计算时采用单精度的分离式求解器，湍流模型选用Realizable湍流模型。

1.3 计算方法验证

隧道内空气流动属于非圆管的三维不可压缩湍流流动，其流动物理特性与标准圆管内的湍流流动相似，因此本文研究了入口风速6m/s，内径分别为5.2m、5.4m、5.6m、5.8m和6.0m标准圆管内湍流运动研究，将得到的充分发展段断面上的平均风速点到壁面距离值和最大速度值与湍流充分发展段速度分布半经验公式[14-16]的计算值相比较，公式如下：

其中，为圆管内某点的速度，为该点到管壁的距离，壁面的粗糙高度是Δ，*为摩擦速度。

验证计算模型和计算方法的可靠性，对比结果如图3所示。由图可见两种计算结果的变化趋势一致，且误差在5%以内。因此本文针对隧道内的速度分布采用的数值计算方法是准确的。

图3 数值计算与公式计算结果对比

2 区间隧道内活塞风速范围的确定

以重庆某轨道交通线为研究基础，选取其中一个典型的地下车站及与其相连的区间隧道，根据该轨道交通线路的设计参数确定了8个车站相连的单线隧道一维计算模型，如图4所示。模型线路全长为10.6km，车站隧道的长度为140m，断面积为20.545m2；车站站台端至区间隧道之间的过渡段隧道长30m，断面积为29m2；两站之间的区间隧道长取1km，断面积为23.32m2；活塞风井高度为20m，格栅自由面积为16m2；隧道考虑为直线，坡度考虑为0。

图4 隧道一维计算模型网络节点图

地铁列车选用A型车，车体正面投影面积为11.45m2，长度为122m，最高运行速度为80km/h。列车平均加速度及列车平均减速度均为0.62m/s2。行车对数为30对/h。

利用SES软件对多列地铁列车在整条线路上的运行进行动态模拟一段时间后，截取D站停靠的列车即将发车的时刻，从该时刻开始，逐秒计算该列车从D站开始起步直至抵达前方车站E的过程中区间隧道内的风速大小变化。同时建立与D站、E站以及两站间区间隧道相对应的三维计算模型，计算与一维数值计算相同过程中活塞风的变化。

图5 计算结果对比

图5为一维和三维计算模型得到的区间隧道活塞风速，由图可见两种计算得到的活塞风速曲线吻合良好。此外计算结果还表明区间隧道内活塞风速与列车速度的变化规律基本一致，且区间隧道内活塞风速大小变化范围大致为1.74m/s～9.84m/s。

通过以上计算结果，针对区间隧道内的测点选取进行研究时，考虑的隧道内平均风速范围为2m/s～10m/s。

3 风速监测点位置选取的研究分析

根据第2节确定的区间隧道风速范围，分别研究风速入口平均风速分别为2m/s、4m/s、6m/s、8m/s及10m/s工况下，湍流充分发展段内距风速入口400m的隧道断面上的风速分布。本文拟通过两种思路来对风速监测点的位置选取进行分析研究，第一种基于布置一个风速测点，使该点所测得的风速值能直接反映出隧道内的平均风速，第二种给定一个函数关系，通过修正监测结果从而得到隧道平均风速。

风速监测点位置选取的首要原则是不影响列车行车安全性，其次应该避开断面上线等结构产生的涡流区的影响，另外还需兼顾安装维护方便，以保证能够长期获得出准确可靠的数据。通过以上分析可知，相对比较合适布置风速监测点的位置区域只有图6中的区域1和区域2。为了便于分析对比，对区域1与隧道断面圆心平齐的高度直线和区域2过隧道断面圆心与水平线成45度夹角的直线上的点进行研究，测点具体位置如图6所示。

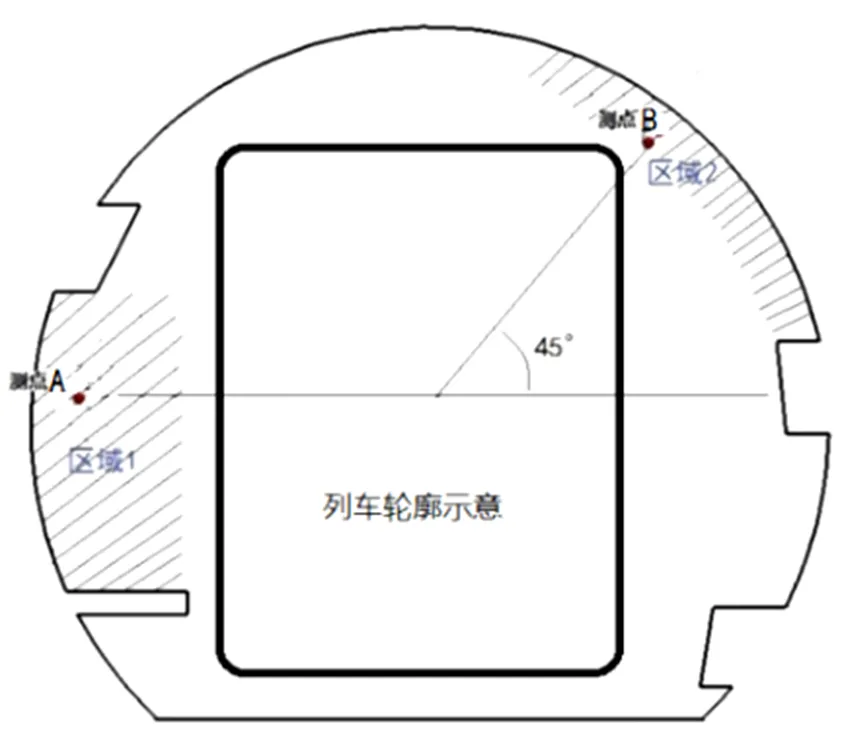
图6 监测点位置选取示意

3.1 基于平均风速点监测方法的研究

由表1和表2中计算结果可知，当隧道内平均风速相同时，平均风速点到隧道壁面的距离随着隧道直径增大而增大；对于同一直径尺寸的隧道，当隧道内的风速增大时，由于隧道本身圆缺形状和安全通道，管线等凸起结构造成隧道断面上的各向非同性，从而导致平均风速点与隧道壁面的距离随着平均风速的增大而减小，这与相应圆管规律不一致。

由上可见对于同一区间隧道，平均风速点的位置会随平均风速的改变而改变，且平均风速点离壁面的距离基本上都大于0.5m，在该位置布置监测点会影响安全通道上人员通行和列车的行车安全，因此将监测点布置在隧道断面上平均风速点的位置来监测隧道平均风速的方法是不可行的。

3.2 基于修正风速监测值监测方法的研究

在图6中区域1和区域2的直线上，离壁面垂直距离为200mm和300mm的地方，分别选定风速监测点A1、A2、B1和B2。表3显示了各工况下四个监测点的风速值。对表中数据进行分析可知，监测点风速随平均风速的变化大致呈线性。由于受篇幅限制，本文仅给出了5.6m直径隧道的监测点风速变化曲线图，如图7所示。

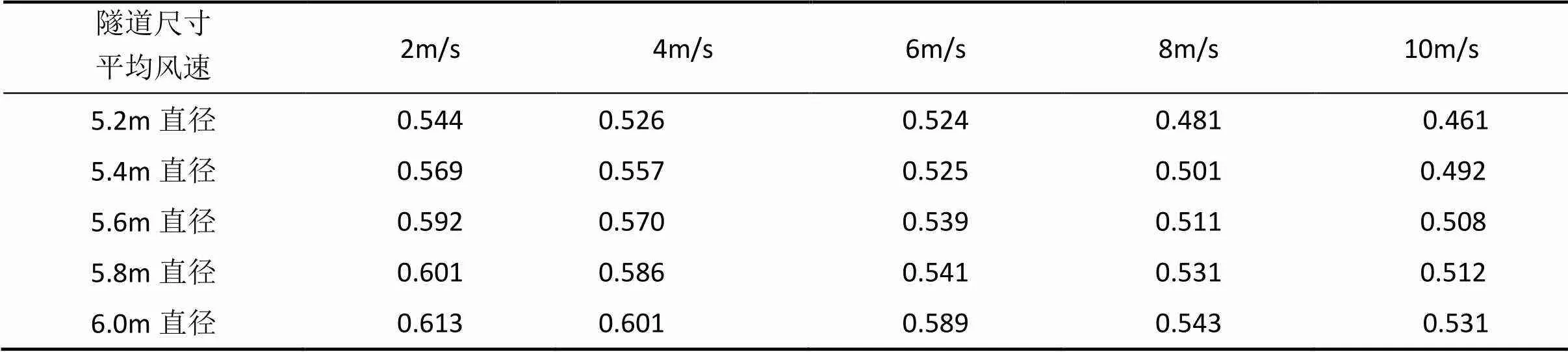
表1 平均风速点A离隧道壁面垂直距离（单位：m）

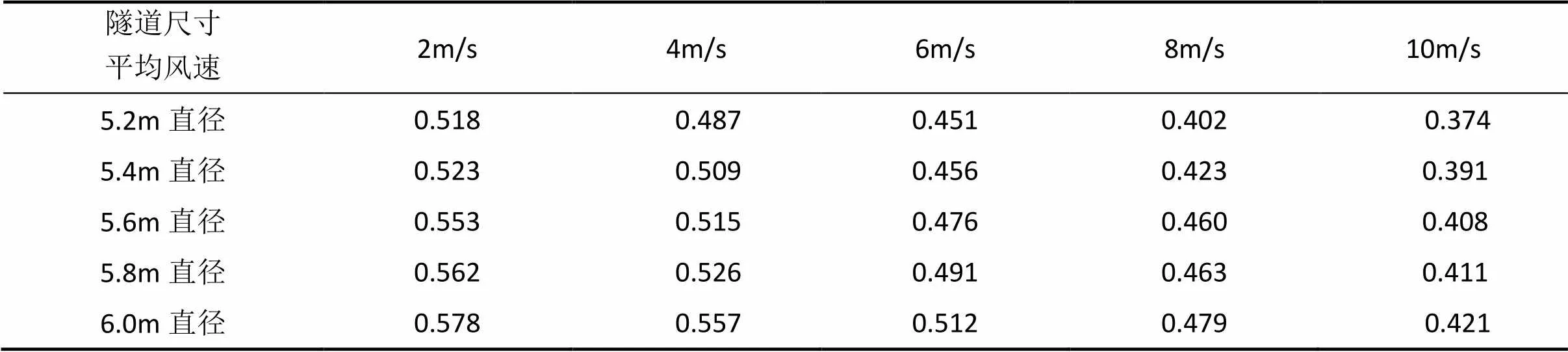
表2 平均风速点B离隧道壁面垂直距离（单位：m）

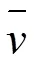
表3 风速监测点风速值（单位：m/s）

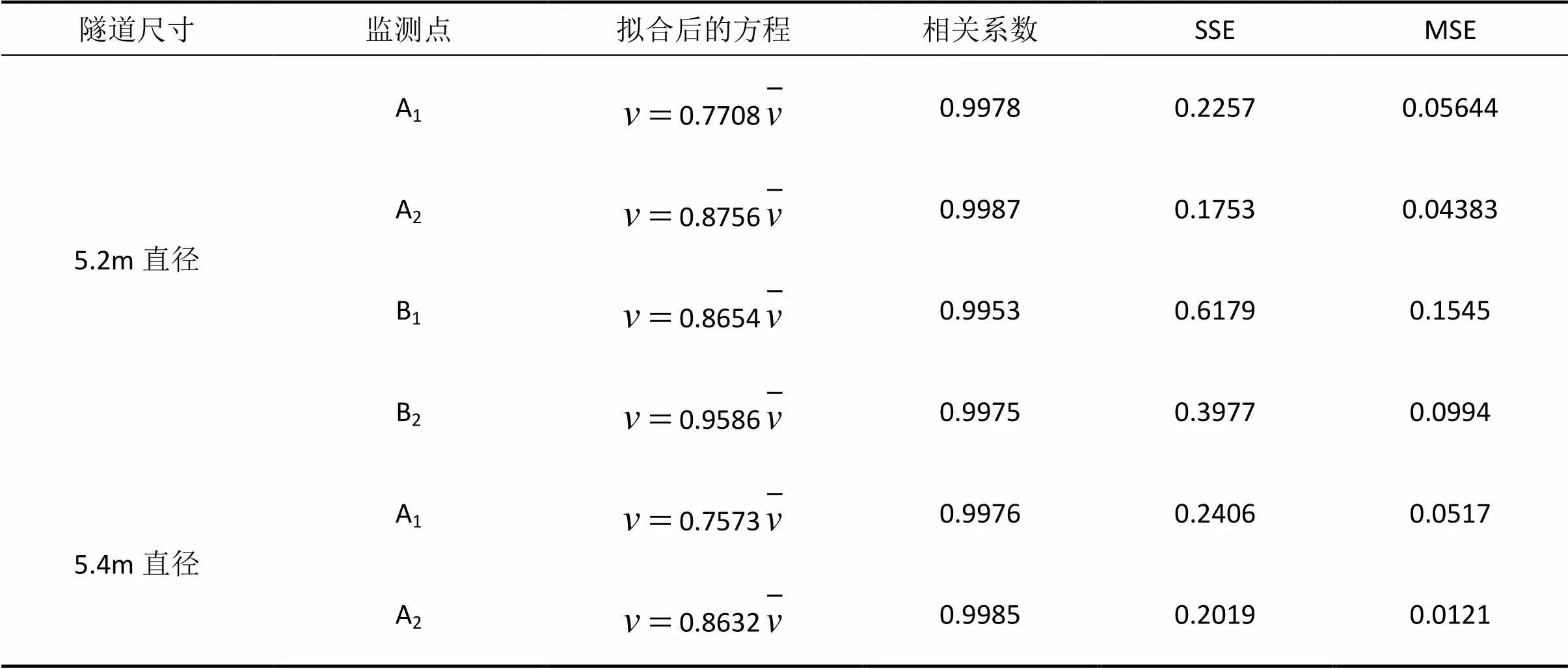
表4 不同直径隧道各监测点风速拟合方程

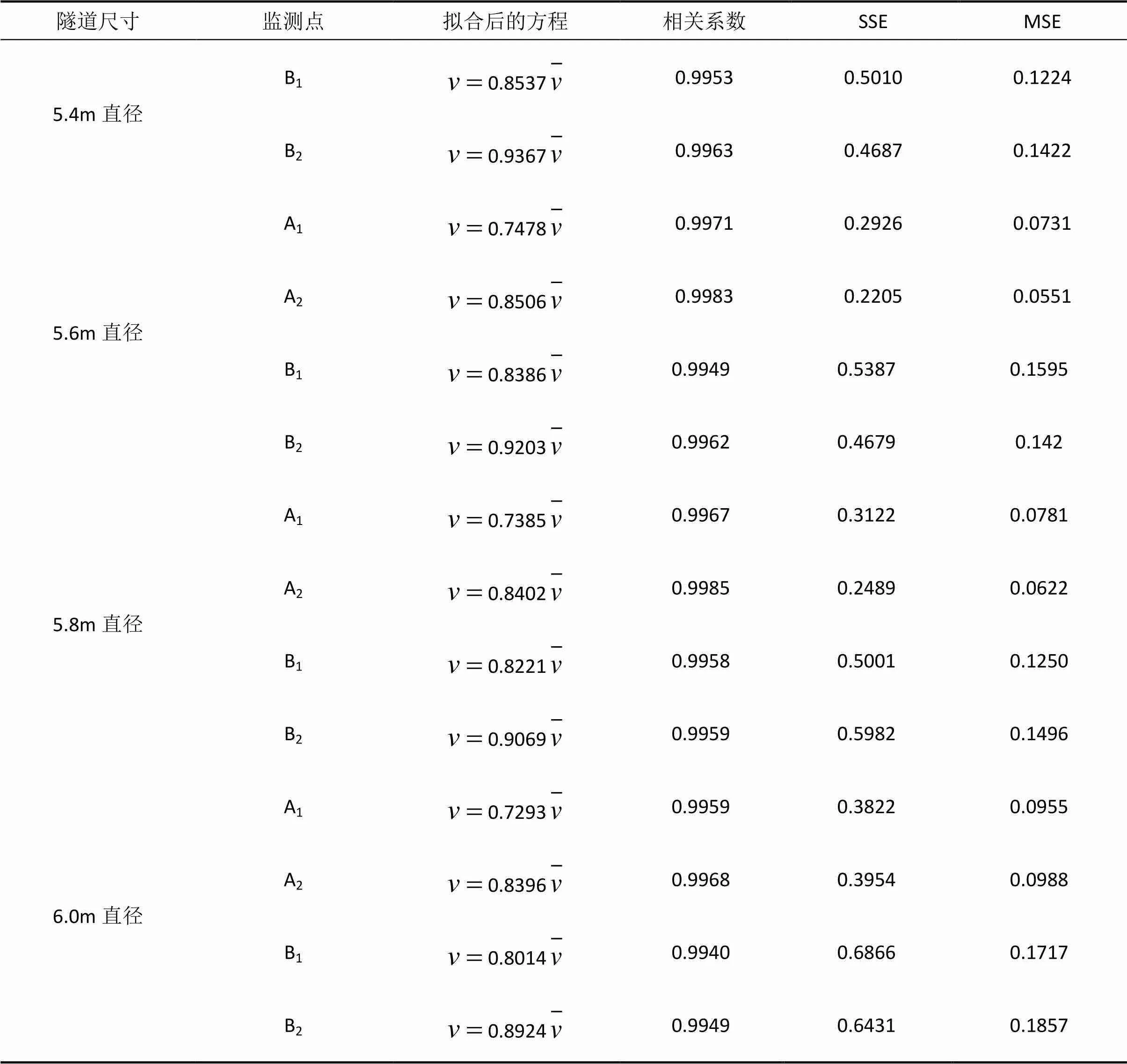
续表4 不同直径隧道各监测点风速拟合方程

4 结论

（1）地铁区间隧道内的活塞风速一般在2m/s～10m/s之间。

（2）由于受车辆限界的限制，将地铁区间隧道风速监测点布置在断面平均风速点位置直接测得隧道平均风速的方法是不可行的。

（3）在隧道靠近壁面较空旷且不影响地铁列车行驶安全的区域布置风速监测点，通过修正监测点风速得到隧道内的平均风速，从而对区间隧道内平均风速进行监测方法是可行的。

（4）隧道内监测点风速与隧道平均风速呈线性关系，且监测点离隧道中心越近，线性关系的相关性越高。

[1] 吴喜平.地铁与热环境[J].能源技术,1999,(4):37-39.

[2] Ming-TsunKe, Tsung-CheCheng, Wen-Por Wang. Numerical simulation for optimizing the design of subway environment control system[J]. Building and Environment, 2002,37(8):1139-1152.

[3] 王丽慧.地铁活塞风与地铁环控节能[D].上海:同济大学,2007.

[4] 豆鹏亮.地铁活塞风与新型屏蔽门环控系统的数值研究[D].上海:东华大学,2013.

[5] 赵蕾,王君,胡浩明,等.基于实测的西安地铁二号线活塞风特性分析[C].2014年铁路暖通年会,2014.

[6] 王树刚,江亿,朱颖心.北京地铁列车活塞风的实测与分析[J].暖通空调,1998,(5):47-49.

[7] 郝元伟,陈开岩,蒋中承,等.基于CFD模拟的港道风速监测值修正处理[J].煤炭安全,2011,42(2):1-3.

[8] 王翰锋.基于Fluent巷道断面平均风速点定位监测模拟研究[J].煤炭科学技术,2015,43(8):92-96.

[9] 暨朝颂.管流中湍流速度分布函数[J].中国矿山工程,2013,42(4:63-67.

[10]鲁华伟,毕海权,周阳,等.高纬度寒区隧道施工热环境数值计算研究[J].制冷与空调,2016,30(2):2015-207.

Study on the Selection of Air Velocity Monitoring Point for Circular Subway Interval Tunnel

Wang Fangyu Bi Haiquan Wang Honglin Cao Song

( School of mechanical engineering, southwest Jiaotong university, Chengdu, 610031 )

In order to determine the reasonable air velocity monitoring point layout position of average air velocity monitoring in the circular subway interval tunnel, the numerical simulation method is used to analyze the size of velocity and distribution of air velocity in the cross section in the tunnel. The result show piston wind speed in the interval tunnel is 2m/s～10m/s. It is feasible to install the air velocity monitoring point in the area close to the wall and does not affect the safety train, and obtain the average air velocity in the tunnel by modifying the air velocity of the monitoring point. At the same time, the relationshipbetween the air velocity at the monitoring point and the tunnel diameter and the average air velocity is summarized. The air velocity of monitoring point is linearly related to the average air velocity in the tunnel l, and the monitoring point is closer t to the center of the tunnel, the linear correlation is higher.

Subway interval tunnel; air velocity monitoring point; Average air velocity; distribution of air velocity; numerical calcucation

1671-6612（2018）01-071-07

TU834/U231.5

A

王方宇（1990.3-），男，在读硕士研究生，E-mail：wfangyu123@163.com

毕海权（1974.12-），男，教授，E-mail：bhquan@163.com

2017-06-01