蓄热式热交换器的结构改进及其影响因素的研究

陈 强 冯 毅 范继珩



蓄热式热交换器的结构改进及其影响因素的研究

陈 强 冯 毅 范继珩

（华南理工大学机械与汽车工程学院化工机械与安全工程研究所 广州 510640）

蓄热式全热交换器被广泛应用于空调新风、烟气排放等系统中进行能量回收。对蓄热式热交换器进行了结构的改进，运用数值分析方法综合探究了蓄热式全热交换器的热交换规律，并初步建立了蓄热式全热交换器的蓄热体长度、换向时间与换热效率的数学模型，重点探究了不同因素对全热交换器热效率的影响，为蓄热式全热交换器的设计和使用奠定了理论基础。

蓄热式；热交换器；结构改进；影响因素

0 引言

空调新风系统中进行能量回收的热交换器在改善室内空气质量的同时，又能进行高效的能量回收，实现了空气流通与能源节约的双赢，因此热换热器的优化设计必然是今后重要的发展方向之一。目前，根据能量回收装置的的结构形式的不同[1]，可以分为转轮式全热交换器、静止平板式全热交换器、热管式全热交换器、盘管或双塔回收环式等几大类[2]，其中转轮式和静止平板式能够进行全热换热，使得他们的能量回收性能在绝大多数情况下远优于其他只能进行显热换热的热交换器。

蓄热式热交换器一般设计成转轮式，是由蓄热材料构成的转芯交替转过新风和排风通道来进行传热和传质[3]，板式全热交换器则直接通过两通道之间的隔板进行传递能量。在同等的使用环境中，转轮蓄热式全热交换器的总传热效率要略优于板式全热交换器[4]，然而，转轮式全热交换器复杂的转轮机构使得其安装和维护成本要高于板式全热换热器，造成转轮式全热换热器的使用范围反而要低于板式全热换热器[5]，因此对蓄热式全热换热器结构的优化设计显得尤为重要。

1 蓄热式全热交换器结构优化设计

综合考虑转轮蓄热式热交换器转芯制作工艺及维护的复杂，是其市场拥有率较低的主要原因之一，因此若去除其转轮结构，则可以在拥有较高换热效率的同时，兼顾简化结构的优势[6]。优化后的蓄热式全热交换器结构如图1所示，在两个完全相同的的通道中，一侧端口分别设置两个完全相同的可逆轴流风机1。通道内部则用蓄热材料3进行填充。同时，在通道两侧端口、蓄热体内部的两侧各放置一个温度传感器2，两个通道中间布置吸湿隔板4。当装置运行时，两个可逆轴流风机在控制器控制下，反向转动，即一个送风，一个排风。送排风过程中蓄热体和空气进行热量交换，蓄热体温度变化。蓄热体内部的四个温度传感器会源源不断的将温度信息送达控制器，当温度达到最佳设定值时，控制器控制两台风机各自反转，原来送风通道变为排风通道，排风通道变为送风通道。风向的改变使空气与蓄热体之间进行逆向的热量传递。这一相反过程的实现，能达到余热回收的目的。同时，通道外部两侧的温度传感器能分别检测到室内和室外的温度，控制器通过比较两者的温度差值来调节可逆轴流风机的转速。当室内外温差较大时，风机输出较大转速，充分利用温差带来的传热效率高这一优势；当室内外温差较低时，风机输出较低转速，空气和蓄热体之间能够进行充分的换热。

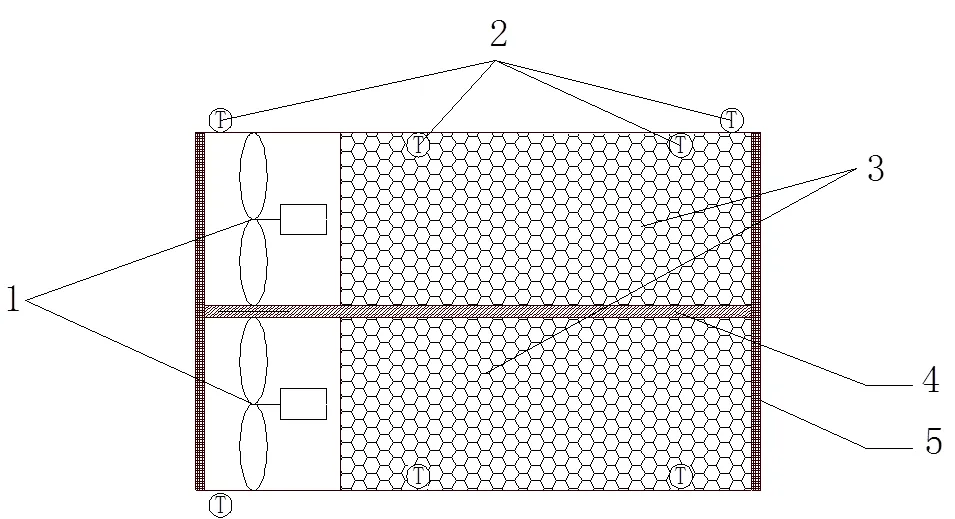
图1 蓄热式全热交换器

送风过程中蓄热体和空气进行热量交换，蓄热体温度变化。蓄热体内部的四个温度传感器会源源不断的将温度信息送达控制器，当温度达到最佳设定值时，控制器控制两台风机各自反转，原来送风通道变为排风通道，排风通道变为送风通道。风向的改变使空气与蓄热体之间进行逆向的热量传递。这一相反过程的实现，能达到余热回收的目的。同时，通道外部两侧的温度传感器能分别检测到室内和室外的温度，控制器通过比较两者的温度差值来调节可逆轴流风机的转速。当室内外温差较大时，风机输出较大转速，充分利用温差带来的传热效率高这一优势；当室内外温差较低时，风机输出较低转速，空气和蓄热体之间能够进行充分的换热。

这种结构形式的蓄热式热交换器取消了转轮机构，而通过改变风向来实现吸热和放热，实现更加容易安装和维护的优化目标。同时，该型蓄热式全热交换器与空调系统一起实现智能化控制，使得传热效率更加稳定。

2 蓄热式全热交换器换热效率影响因素分析

2.1 数学模型的建立

由于换向型的蓄热式全热交换器采用了周期性的工作方式，其蓄热体的吸热和散热可以作为两个完全相反的过程，而且互不干扰，因此两个过程数学模型相同，仅仅是初始边界条件相反[7]。所以蓄热式全热交换器的数学模型就是一个传热过程的数学模型。

为建立传热传质过程的数学模型，可做如下假设：蓄热体构成的每个换热通道传热特性相同；气流流速在任意截面处恒定且温度分布均匀；蓄热体与空气的各物性参数及各处对流换热系数恒定；蓄热体与流动垂直方向的导热远大于轴向方向的传热；忽略辐射传热影响。因此建立模型时仅需考虑轴向方向的温度分布。根据能量守恒，空气和蓄热体的能量方程建立如下：

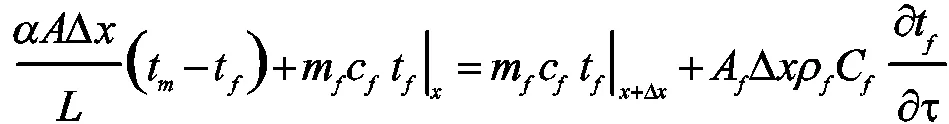
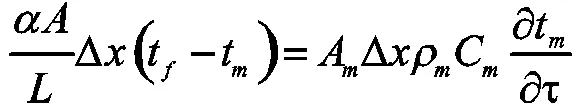
式中：为总换热面积，m2；为蓄热体的长度，m；A、A分别为任意截面流体部分和固体部分的面积，m2；t、t分别为流体和蓄热体的温度，℃；ρ、ρ为蓄热体的密度，kg/m3；C为流体的比热，kJ/kg·℃；m为流体的质量流速，kg/s。

此模型建立在蓄热体内部无轴向导热的假设之上，而在实际的情况之中，有些蓄热体材料的导热系数较大，因此无法忽略其对蓄热式全热交换器换热性能的影响，Willmott[8]等通过实验和理论分析，对两者之间的关系进行了总结，建立了修正关系式。

2.2 蓄热体内部的温度分布数学模型

研究上述数学模型，可以得出新排风的温度、迎风风速、蓄热体的长度等对蓄热式换热器的热效率有较大的影响。然而对于换向型蓄热式热交换器而言，换热周期的确定成为一个不可回避的关键问题。换热周期过短，导致流体与蓄热体之间换热不充分，热效率大大降低；换热周期过长，则会造成不必要的浪费，无法达到节约资源的目的。通过对换向型蓄热式热交换器的工作原理进行分析，为避免换热周期的过短或过长，蓄热体的温度分布和换热饱和期的研究显得至关重要。因此，通过温度前沿扩展理论来分析蓄热器内部温度分布，并以此为基础，探究换热效率随时间的变化关系，从而选择一个较高换热效率的换向时间。

采用数理统计分析法对混合扩散一中心对称模型进行分析，最终得到蓄热式热交换器内部蓄热体的温度的梯度变化，其数学描述为[9]：

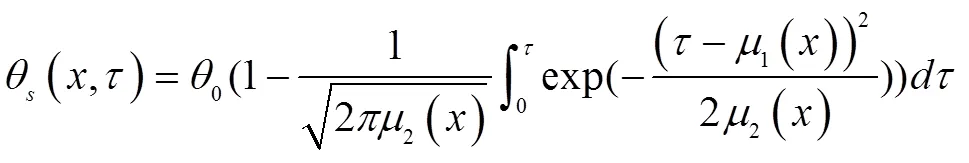
其中：

其中：

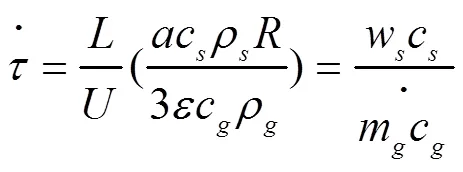
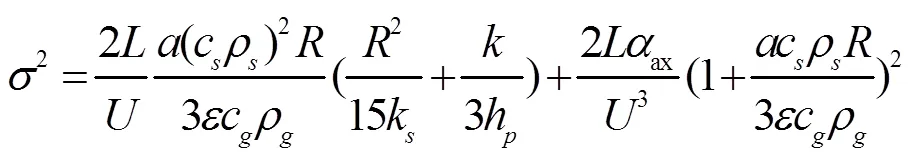
再结合佩格列数的推导公式：

可以将特征值方程写为：

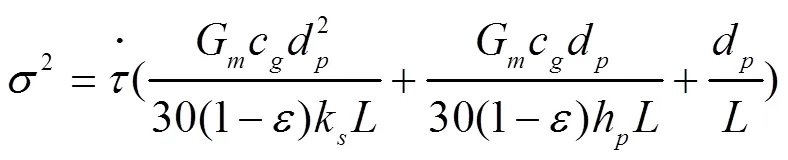
由式（10）可知，蓄热体上温度分布随时间的变化是一S型曲线。其基本图像如图2所示。这些曲线上的点代表蓄热体轴向的温度分布变化，通过分析建立的数学模型充分认识

图2 蓄热体温度随时间在长度方向的变化曲线

2.3 影响热交换器换热效率的因素分析

分析本热交换器建立的数学模型，其曲线的形态仅仅取决于2，因此在进行换热效率因素分析时，可以通过对2的分析来确定蓄热体结构长度、换向时间等因素对换热效率的影响。现在我们引入一个常数A，对式（10）进行变形，可以得到一新的数学模型：

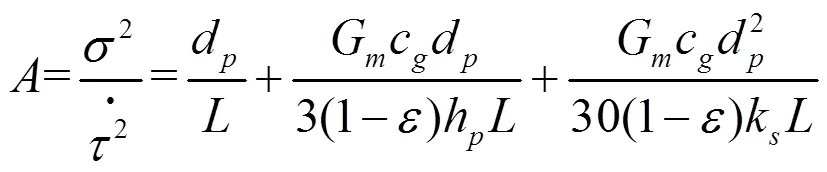
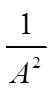
（1）换热器长度的影响

蓄热体物理模型为d=0.005m，流体流速=0.5m/s，蓄热体的导热系数为k=206W/m·℃。图3是根据建立的数学模拟计算结果，根据变化曲线可知，当蓄热体长度越长时，其换热更加充分，蓄热体的换热效率越高。但是在实际操作过程中，蓄热体的长度不可能无限长，因此需要选定一个比较合理的长度范围，既能够达到较高的换热效率，又能够最大程度的节约空间和制造成本。仔细分析图表的变化，蓄热体的长度在0.3m之后，随蓄热体长度的加长，常数变化幅度较小，可以视为其换热效率增加不太明显，因此可以取蓄热体长度在0.3m-0.4m之间是一种比较合理的选择。

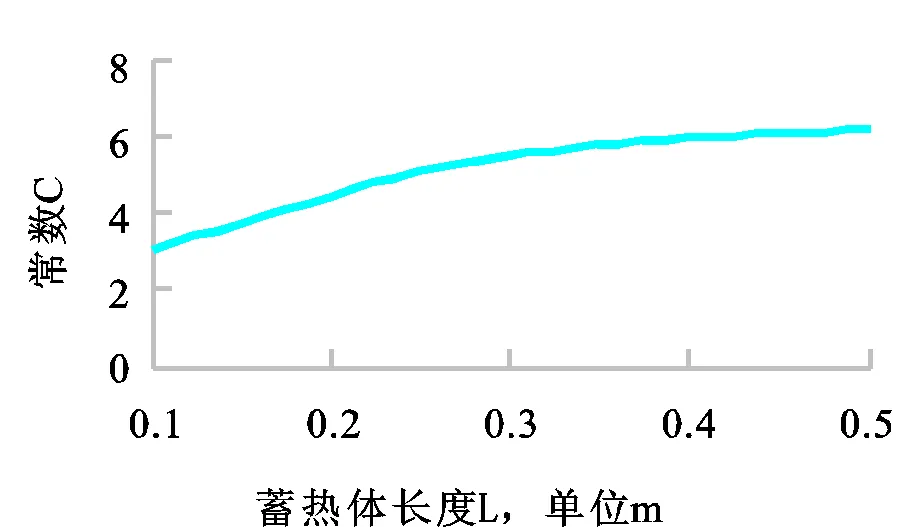
图3 C值随蓄热体长度的变化关系图

（2）蓄热体当量直径d的影响

在其他条件不变的情况下，选取0.3m的长度作为蓄热体长度，蓄热体的当量直径与常数的关系如图4所示。观察图形可知，随着当量直径的变化，换热器的换热效率有着较大的变化，较小的当量直径伴随着较高的换热效率，当当量直径增大时，其换热效率迅速降低，主要原因是热阻的增加以及相对换热面积的减少，影响了其综合传热能力，因此在进行交换器设计时，换热器的结构尺寸是一个非常重要的考虑因素。

图4 C值随蓄热体当量直径的变化关系

（3）流体流速的影响

选取蓄热体的当量直径d=0.005m，导热系数k=206W/m·℃，蓄热体长度=0.3m，对不同流体流速下的常数的变化关系进行模拟运算，如图5所示。对于一个固定的蓄热式换热器而言，增加流体流速会增加其对流换热系数，但观察曲线特征，换热器的换热效率随流体流速的增大反而逐渐较小，因此，一味的追求过高的流体流速对于换热器的换热效率而言是一种巨大的效率损失，因此流速的确定对于换热器的设计显得至关重要。

图5 C值随蓄热体流体流速的变化关系

（4）导热系数k的影响

图6是导热系数k对值的影响关系曲线，观察曲线，两者的关系并非单纯的线性关系，当蓄热体由导热系数较小的材料替换为导热系数较大的材料时，换热器的换热效率提升较大，但是当材料的导热系数大到一定程度时，即导热系数在200W/m·℃以上时，换热效率的变化就较为缓慢。因此，蓄热换热器的蓄热体的导热系数对其换热效率有较大影响，应首先选择导热性能好的材料做为蓄热体，但也不能过分的选择更大的导热性能，这对提升换热效率并无较大的好处，反而容易造成较大的材料浪费。

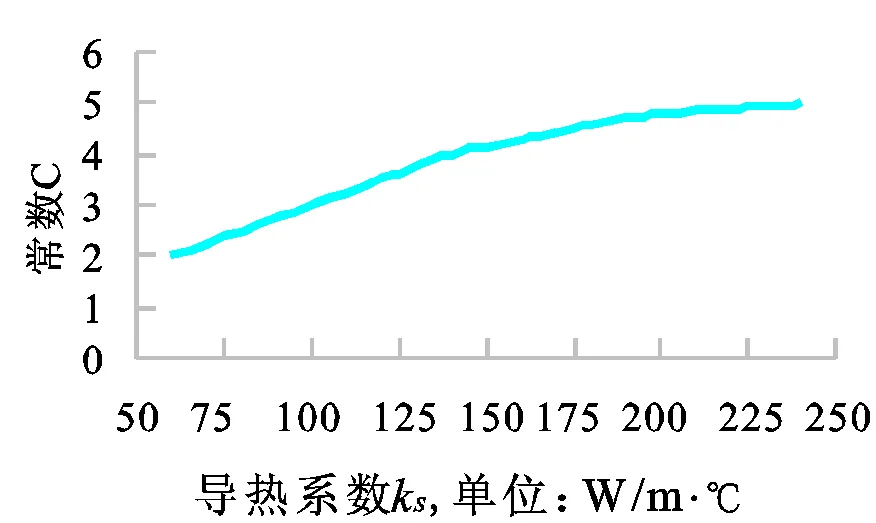
图6 C值随蓄热体导热系数的变化关系

4 结论

本文对蓄热式热交换器的结构进行了改进，提出了一种新的蓄热式空气-空气能量回收装置，采用了双通道的蓄热式结构，大大简化了设计和制造的难度。同时对该结构的蓄热式热交换器进行了数学分析，建立了适合新结构的数学模型，为蓄热式热交换器的结构选型和设计提供了最基本的理论基础。在该模型基础上，采用数值分析的方法，得到了最佳的蓄热体长度、当量直径、流体流速以及导热系数的选择，对实际的蓄热体的设计也具备一定的借鉴和意义。

[1] 邱相武.新风利用与热回收的动态分析与研究[D].北京:中国建筑科学研究院,2001.

[2] 刘俊杰,王斌.全热交换器效率的权重系数分析方法[J].天津大学学报,2007,40(8):943-947.

[3] 秦伶俐,李洪芳.转轮式全热交换器-一种高效的热回收装置[J].制冷,1998,(3):20-23.

[4] 李芳,林泽安,彭飞,等.全热交换器交换效率影响因素的试验研究[J].制冷与空调,2010,10(2):50-52.

[5] 崔中坚,刘刚,王海,等.蓄热式换热器的仿真模拟与研究[J].建筑热能通风空调,2010,29(3):5-7.

[6] 王瑞,王义春,冯朝卿,等.空调全铝新型换热器结构优化与性能研究[J].北京理工大学学报,2012,32(7):700-704.

[7] 王立峰,曹阳,陈方圆,等.空气－空气能量回收装置交换效率影响因素的试验研究[J].暖通空调,2013,43(12): 141-144.

[8] A J Willmott, A Bures. Transient Response of Performance of Periodic-Flow Regenerators[J]. Int. J. Heat Mass Transfer, 1997,(20):753-761.

[9] 赵静野,李建树.蓄热式热交换器数学模型的比较[J].北京建筑工程学院学报,2003,19(2):2-5.

Study on the Structure Improvement and Influencing Factors of Regenerative Heat Exchanger

Chen Qiang Feng Yi Fan Jiheng

( Institute of Chemical Machinery and Safety Engineering, School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou, 510640 )

Regenerative heat exchangers are widely used in air conditioning, fresh air and flue gas emission systems to carry out energy recovery. This paper improves the structure of regenerative heat exchanger, and use the numerical analysis method to explore heat exchanger heat exchange law, and establishes the regenerative heat exchanger mathematical model of the regenerator length, reversing time and heat transfer efficiency, point to explore the impact of different factors on the heat exchanger efficiency, which laid a theoretical foundation for the design and use of regenerative heat exchanger.

Regenerative; heat exchanger; Structure improvement; influence factor

1671-6612（2018）01-014-04

TB657.5

B

陈 强（1992.05-），男，硕士研究生，E-mail：cqsdust@163.com

冯 毅（1963.03-），男，博士后，副教授，E-mail：mmyfeng@scut.edu.cn

2017-06-21