轮毂电驱动汽车乘坐舒适性研究
郑 琦,杨旭凯,黄文岗,郭洪艳
0 引 言
随人们对汽车需求的不断增加,汽车的保有量连年增长,截止2015年底,我国机动车保有量达2.79亿辆,其中汽车1.72亿辆。新能源汽车保有量达58.32万辆,其中纯电动汽车保有量达33.2万辆,占新能源汽车总量的56.93%,与2014年相比增长了317.06%。可见电动汽车的发展前景日益广阔[1]。而且,截止到2015年底,机动车驾驶人已达3.27亿,其中汽车驾驶人超过2.8亿。可见汽车的需求量还远远没有达到饱和。而日益增长的汽车数量相对于不可再生的石油能源,使人们对电动汽车的发展给予了更大的关注[2]。
轮毂电驱动汽车的出现,使人们对悬架,非簧载质量和乘坐舒适性等有了新的认识[3]。与传统主动悬架相比,轮内电驱动汽车用驱动电机取代了传统的发动机,用主动悬架取代了传统悬架[4]。并将驱动电机和主动悬架都集成在车轮内部,使汽车的结构更紧凑,没有了传统的发动机、离合器、变速器、传动轴、差速器和机械悬架系统等结构[5]。从而使汽车的整体质量减轻,更节能,可实现驾驶员期望的续驶里程。但非簧载质量增加使乘坐舒适性变坏。为提高乘坐舒适性,驱动电机的质量成为重要的指标[6]。
目前国内外对乘坐舒适性的评价指标主要是基于车身与车轮两自由度车辆振动系统模型的车身加速度对路面输入速度的幅频响应特性。通过分别分析车轮不动时,将车身质量当做单自由度无阻尼自由振动系统,以及车身不动时,把车轮质量当做单自由度无阻尼自由振动系统描述[7]。笔者基于车身与车轮两自由度四分之一车辆振动系统模型[8],推导出不变点,并利用Simulink搭建模型加以验证,说明轮毂电驱动汽车乘坐舒适性变坏的原因,即是由于驱动电机的增加造成了乘坐舒适性变差,因此给出了驱动电机的质量要求。
1 四分之一车辆振动系统建模
实验以某国产车型结构参数[9]为例进行计算和仿真,具体参数如表1所示。

表1 某国产车型结构参数Tab.1 Structural parameters of a domestic automobile model
1.1 建立时域滤波白噪声路面输入系统数学模型
根据文献[10]中标准,路面功率谱密度

其中n为空间频率,它是波长λ的倒数,单位为m-1;n0=0.1 m-1为参考空间频率;Gq(n0)为参考空间频率n0下的路面功率谱密度值,称为路面不平度系数,单位为m3;W为频率指数,为双对数坐标上斜线的斜率,它决定路面功率谱密度的频率结构。路面不平度8级分类标准如表2所示。

表2 路面不平度分类标准Tab.2 Classification standard of road surface roughness
当汽车以一定车速u(m/s)驶过空间频率n(m-1)的路面不平度时,输入的时间频率[11]

时间频率功率谱密度和空间频率功率谱密度的关系如下

将式(1)~式(3)联立求解得

将分级路面谱的频率指数W=2代入式(4)得

将 ω=2πf代入式(5)得

假设截止频率为ω0,则式(6)变换成
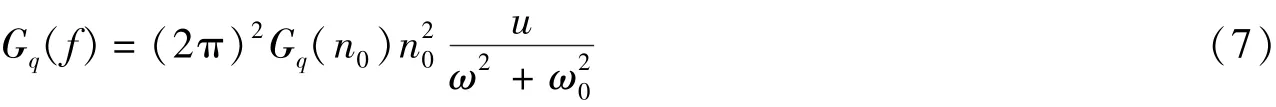
式(7)可视作白噪声激励的一阶线性系统的响应,根据随机振动理论,可知

其中H(ω)为频响函数;Sω为白噪声W(t)功率谱密度,取Sω=1。所以有

即
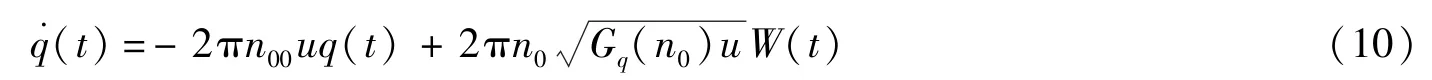
其中n00=0.011 m-1为下截止空间频率;q(t)为路面随机高程位移(m);W(t)为均值为零的高斯白噪声。
1.2 建立车身与车轮两自由度四分之一车辆振动系统数学模型
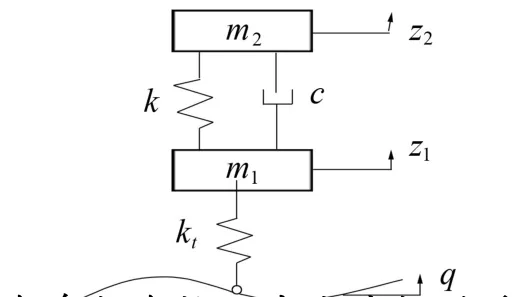
图1 车身与车轮两自由度振动系统模型Fig.1 Two degree of freedom vibration system model of vehicle body and wheel
建立车身与车轮两自由度四分之一车辆振动系统模型如图1所示[12]。假设轮胎没有离开地面,车轮和车身垂直位移坐标z1和z2是从静态平衡位置开始测量的[13],则运动的线性公式可描述为

2 计算分析不变点大小和位置
将式(11)和式(12)相加得到

假设初始值为零,对式(13)进行拉氏变换得
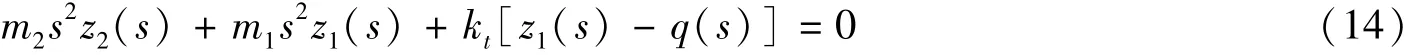
将式(14)变换成如下形式
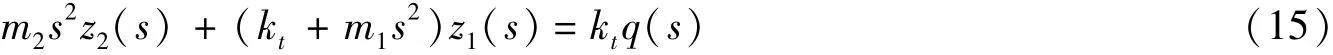
然后定义3个传递函数
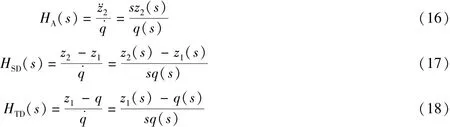
其中HA、HSD和HTD分别是车身加速度传递函数,悬架弹簧动挠度传递函数和轮胎弹性动挠度传递函数。这3个传递函数都是和路面输入速度(˙q)相关的。一般使用输入速度(˙q)的路面是时域滤波白噪声路面。
将式(16)~式(18)代入式(15)得到

将s=jω代入式(19)~式(21)中,得到
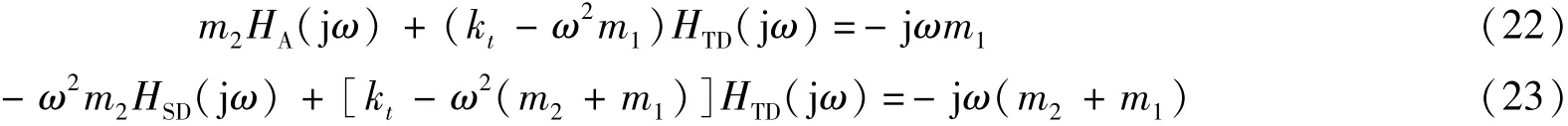
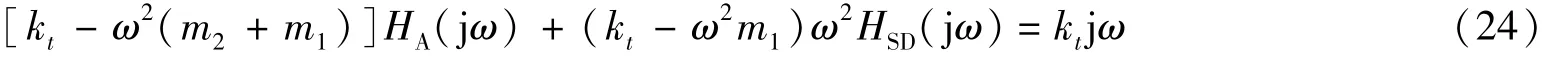
从式(22)~式(24)中看出,一旦3个传递函数中的1个被确定,其他两个传递函数也被确定。式(22)~式(24)可确定传递函数中的不变点,这些不变点的值对应着一些特殊的频率[14],这些特殊的频率只与kt、m1和m2有关。在式(22)中,令含有HTD(jω)的相恒为零,则只需令前面的系数恒为零即可,即kt-ω2m1=0。获得一个和HA(jω)有关的特殊频率ωi= kt/m1。则和其对应的HA(jωi)=j m1kt/m2,这个点定义为车身加速度响应的不变点[15]。多数的车辆ωi的值在10 Hz左右。
3 仿真分析
在Simulink中搭建时域滤波白噪声路面输入系统模型如图2所示[16]。

图2 时域滤波白噪声路面输入系统模型Fig.2 Time domain filtering white noise road surface input system model
选取行驶路面为C级路面,行驶速度为50 km/h,建立车身与车轮两自由度四分之一车辆振动系统Simulink模型[17](见图3)。
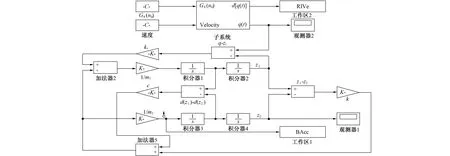
图3 车身与车轮两自由度四分之一车辆振动系统simulink模型Fig.3 Two degree of freedom 1/4 vibration system simulink model of vehicle body and wheel
绘制车身加速度对路面输入速度幅频特性曲线[18]如图4所示,标记的点为不变点。
3.1 改变弹簧刚度k的影响
由于不变点的表达式ωi= kt/m1与弹簧刚度k无关,所以,改变弹簧刚度k(13 000 N/m~20 000 N/m),绘制新的曲线,并观测不变点的位置。仿真结果如图5所示。
将该不变点位置和图4中绘制曲线的不变点位置比较发现,改变参数前后的不变点的位置和改变参数前不变点的位置相同,所以改变参数k对不变点的位置没有影响。
3.2 改变阻尼系数c的影响
由于不变点的表达式ωi= kt/m1与阻尼系数c无关,所以,改变阻尼系数c(1 200 N/(m·s-1)→2 000 N/(m·s-1)),绘制新的曲线,并观测不变点的位置。仿真如图6所示,标记的点为不变点的位置。与图4中绘制曲线的不变点位置比较发现,改变参数前后不变点的位置相同,所以参数c对不变点的位置没有影响。
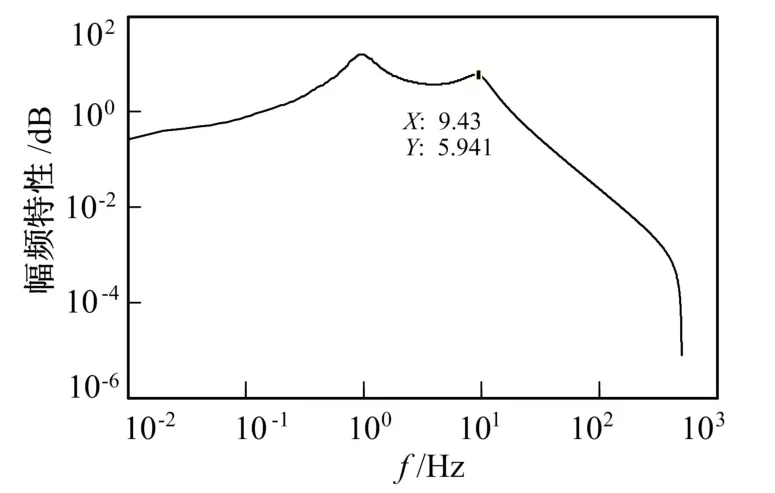
图4 车身加速度对路面输入速度幅频特性曲线Fig.4 Amplitude frequency characteristic curve of vehicle body acceleration

图5 改变弹簧刚度k后的 幅频特性曲线Fig.5 Amplitude frequency characteristic curve after changing spring stiffnessk
3.3 由电机引起的非簧载质量增加对不变点的影响
由于轮毂电机的加入,使非簧载质量增加,即m1增加,根据ωi= kt/m1,导致ωi减小。
改变非簧载质量m1(模拟轮毂电机引起的非簧载质量增加,从43~70 kg,不变点左移),绘制新的曲线,并将原曲线绘制在同一张图中,观测不变点的位置。仿真如图7所示。
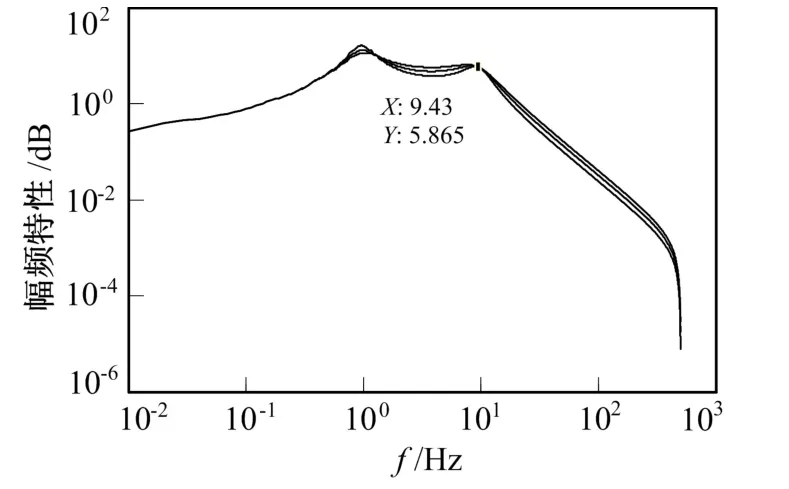
图6 改变阻尼系数c后的幅频特性曲线Fig.6 Amplitude frequency characteristic curve after changing damping coefficient c
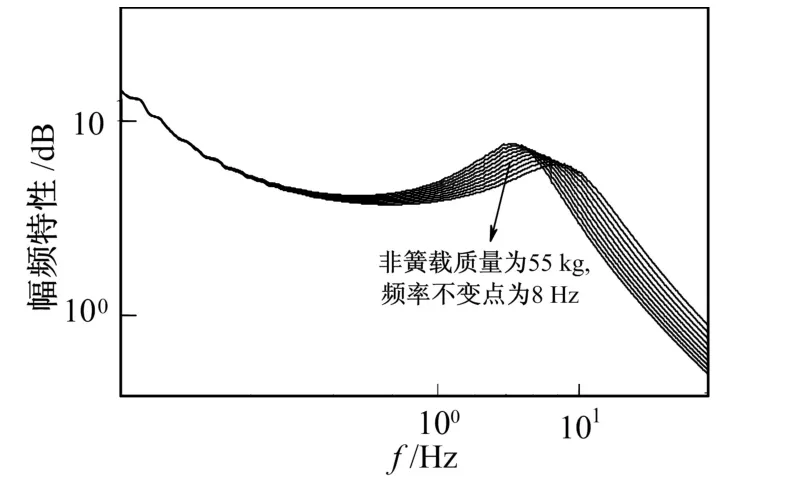
图7 非簧载质量m1改变后的幅频特性曲线Fig.7 Amplitude frequency characteristic curve after the change of non spring load m1
将该不变点与图4中的不变点对比发现,不变点的频率从9.43 Hz减小到7.19 Hz时,频率小于8 Hz。而在4~8 Hz频率范围内,人体内脏器官最容易产生共振,即人感觉最不舒服的频率范围。所以,轮毂电机引起的非簧载质量增加,是引起轮毂电驱动汽车乘坐舒适性变差的根本原因。
3.4 轮胎刚度要求
根据ωi= kt/m1,轮胎刚度 kt变大时,ωi也会随之变大,改变 kt的大小,从100 000~180 000 N/m,仿真如图8所示,轮胎刚度由小变大,不变点右移。
3.5 轮毂电机的质量要求
由于轮毂电机的加入,使非簧载质量增加,即m1增加,根据ωi= kt/m1,ωi减小。不变点频率表达式如下

设轮毂电机的质量为m0,则新非簧载质量为

将式(26)代入式(25)得

由于人体对4~8 Hz频率范围最为敏感,故要使fi>8 Hz,即

所以,可获得轮毂电机质量

其中m1为除轮毂电机以外的非簧载质量(kg)。
由以上仿真结果得知,影响频率不变点变化的因素只有非簧载质量和轮胎刚度。非簧载质量增加,造成不变点的左移,使频率不变点减小到8 Hz以下,影响了乘坐舒适性;轮胎刚度的增加,不变点右移,可以使频率不变点增加。因此,通过协调非簧载质量和轮胎刚度,可得出一组适用的非簧载质量与轮胎刚度的值。
给出一组轮胎刚度与非簧载质量的要求分别为170 000 N/m,55 kg。仿真结果如图9所示。
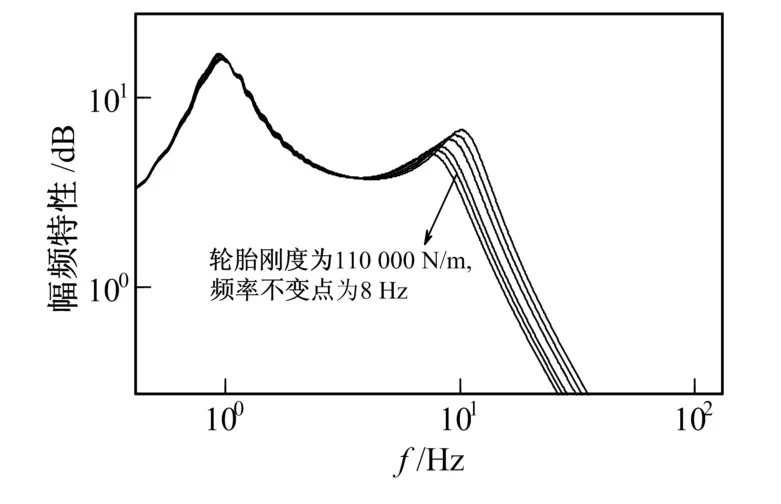
图8 轮胎刚度kt改变后的幅频特性曲线Fig.8 Amplitude frequency characteristic curve of after the change of tire stiffness kt

图9 轮胎刚度为170 000 N/m, 非簧载质量为55 kg的幅频特性曲线Fig.9 The amplitude frequency characteristic curve of tire stiffness of 1 600 and non sprung mass of 10
4 结 语
笔者通过建立车身与车轮两自由度四分之一车辆振动系统模型,推导出车身加速度相对路面输入速度的幅频特性曲线的不变点,进一步说明轮毂电驱动汽车因为非簧载质量增加,使不变点左移进入4~8 Hz范围内,是乘坐舒适性变差的根本原因。通过对弹簧刚度、减震器阻尼系数、非簧载质量与轮胎刚度等一系列变量的仿真,确定了不变点的变化规律,即不变点的改变仅与非簧载质量以及轮胎刚度有关。并通过得出的不变点的变化规律,进行仿真,给出轮毂驱动电机的质量要求,以及轮胎刚度的要求,改善高频段的乘坐舒适性。
[1]孙悦超.电动汽车驱动方式及未来发展[J].电机与控制应用,2016,43(11):98-102.SUN Yuechao.Electric Vehicle Driving Mode and Future Development[J].Electric Machines&Control Application,2016,43(11):98-102.
[2]褚文强,辜承林.电动车用轮毂电机研究现状与发展趋势[J].电机与控制应用,2007,34(4):26-29.CHU Wenqiang,GU Chenglin.Application Status and Developiig Tend of Irr Wheel Motors Used for Electr is Auternobile[J].Electric Machines&Control Application,2007,34(4):26-29.
[3]何仁,张瑞军.轮毂电驱动技术的研究与进展[J].重庆理工大学学报:自然科学版,2015,29(7):10-19.HE Ren,ZHANG Ruijun.Research and Development of In-Wheel Motor Drive Technology[J].Journal of Chongqing University of Technology:Natural Science,2015,29(7):10-19.
[4]周杨.四轮轮毂电机驱动车辆直驶稳定性控制策略研究[D].北京:北京理工大学机械与车辆学院,2016.ZHOU Yang.Research on Straight Line Stability Control Strategy of Four-Wheel Drive Vehicle with Hub Motors[D].Beijing:School of Mechanical Engineering,Beijing Institute of Technology,2016.
[5]李树金.电动物流汽车驱动电机的应用现状及发展趋势[J].物流科技,2017(3):35-37.LI Shujin.The Application Status and Development of New Energy Vehicles Drive Motor Trend[J].Logistics Sci-Tech,2017(3):35-37.
[6]张文建.基于车速估计改进算法的四轮轮毂电动汽车控制策略研究 [D].成都:电子科技大学自动化工程学院,2016.ZHANG Wenjian.Contral Strategy of Four-Wheel Independent Drive Eletric Vehicle Based on Improved Vehicle Velocity Estimation Algorithm[D].Chengdu:School of Automation Engineering,University of Electronic Science and Technology of China,2016.
[7]余志生.汽车理论[M].北京:机械工业出版社,2006:222-224.YU Zhisheng.Automobile Theory[M].Beijing:China Machine Press,2006:222-224.
[8]马英,邓兆祥,谢丹.轮毂电机悬架构型分析与优化[J].中南大学学报:自然科学版,2014,45(9):8-14.MA Ying,DENGZhaoxiang,XIE Dan.Analysis and Optimization of In-Wheel Motor Suspension Configuration[J].Journal of Central South University:Science and Technology,2014,45(9):8-14.
[9]陈俊杰,李兆凯,范传帅,等.基于MatLab的车辆振动响应幅频特性分析 [J].中原工学院学报,2011,22(3):46-47.CHEN Junjie,LI Zhaokai,FAN Chuanshuai,et al.Amplitude-Requency Characteristic Analysis of Vehicle Vibration Response Based on MatLab[J].Journal of Zhongyuan University of Technology,2011,22(3):46-47.
[10]GB/T7031-1986.车辆振动输入路面平度表示方法[S].长春:国家标准局,1986.GB/T7031-1986.Vehicle Vibration-Describing Method for Road Surface Irregularity[S].Changchun:National Bureau of Standards,1986.
[11]吴凯,刘梦安.基于Matlab的汽车半主动悬架振动控制[J].机械工程与自动化,2017(1):77-80.WU Kai,LIU Meng'an.Vibration Control Based on MATLAB of Vehicle's Semi-Active Suspension[J].Mechanical Engineering&Automation,2017(1):77-80.
[12]高欣然.基于轮毂电机四轮驱动的电动试验车总体设计[D].西安:长安大学汽车学院,2016.GAO Xinran.Based on Hub Motor Four Wheel Drive Electric Experimental Vehicle Design[D].Xi'an:School of Automoble,Chang'an University,2016.
[13]杨蔚华,方子帆,何孔德.四轮独立驱动电动轮汽车的平顺性仿真研究[J].计算机仿真,2016,33(9):89-93.YANG Weihua,FANG Zifan,HE Kongde.Simulation Research on Ride Comfort of Four In-Wheel Motors Independent Driven Electric Vehicle[J].Computer Simulation,2016,33(9):89-93.
[14]徐明欣,余双金,施善.四分之一车辆悬架系统随机振动分析[J].装备制造技术,2016(9):15-17.XU Mingxin,YU Shuangjin,SHI Shan.Random Vibration Analysis of Quarter-Car Suspension System[J].Equipment Manufacturing Technology,2016(9):15-17.
[15]CHEN Hong,GUO Konghui.Constrained H∞Control of Active Suspensions:An LMI Approach[J].IEEE Trans Contr Syst Technol,2005,13(3):412-421.
[16]赵旗,王维,李杰,等.基于滤波白噪声的汽车平顺性时域建模和仿真 [J].科学技术与工程,2016,16(27):283-287.ZHAO Qi,WANG Wei,LI Jie,et al.Modeling and Simulation of Time Domain for Automotive Ride Comfort Based on a Filtered White Noise[J].Science Technology and Engineering,2016,16(27):283-287.
[17]靳彪,张欣,彭之川,等.四轮轮毂电机驱动电动汽车建模与仿真[J].中国公路学报,2016,29(4):138-144.JIN Biao,ZHANG Xin,PENG Zhichuan,et al.Four Hub-Motor-in-Wheels Drive Electric Vehicle Modeling and Simulation[J].China Journal of Highway and Transport,2016,29(4):138-144.
[18]靳晓雄,张立军,江浩.汽车振动分析[M].上海:同济大学出版社,2002:267-269.JIN Xiaoxiong,ZHANG Lijun,JIANG Hao.Vibration Analysis of Automobile[M].Shanghai:Tongji University Press,2002:267-269.

