互联网环境下基于消费者搜索的酒店入住率预测研究
张斌儒,刘树林,张超锋,蒲玉莲
(1.长江师范学院 a.财经学院,b.管理学院 重庆 408100;2.对外经济贸易大学 国际经济贸易学院,北京 100029)
一、引 言
酒店是旅游业的重要组成部分,在旅游发展中扮演着举足轻重的角色,预测将来酒店需求是酒店收益管理的关键环节,有助于相关企业和组织分配有限的旅游资源以保持市场竞争力[1-2]。然而,诸如酒店入住率等旅游需求是一个复杂的非线性系统,受季节性、突发事件以及随机因素等影响较大,使得传统的预测技术无法对其进行精确的拟合。本文试图寻求更为有效的预测工具对酒店入住率进行预测。
传统的预测方法主要依赖于预测变量或被预测变量的历史数据,预测变量主要包括客源地人口数量、汇率、收入水平、目的地或竞争地门票价格以及其它定量指标[2],这些变量常难以获取。而被预测变量的历史观测往往无法充分拟合旅游需求的非线性特征,数据的发布存在一定的滞后,且要求稳定的经济环境,这在一定程度上限制了模型的应用,影响预测的时效性。近年来,随着信息技术的发展以及互联网的普及,作为旅行计划和在线交易的工具,网络的使用产生了一类可利用的网络搜索数据,这些数据具有实时性、易获取、对消费者行为敏感等特征,一定程度上反映了消费者的潜在旅游需求[3]。
基于互联网的消费者搜索数据(Consumer Search Queries,CSQ)在旅游需求预测领域已有应用。比如,Choi和Varian应用谷歌趋势数据预测来自9个不同国家的到港游客量[4];Yang等采用百度网络搜索数据对中国海南省旅游景区接待的客流量进行了预测研究,并得到了较好的预测效果[5]。王炼和贾建明以“黄金周”期间的客流量数据为研究对象,利用百度搜索指数对短期游客流量成功进行了预测[6];李霞和曲洪建基于百度搜索数据对邮轮旅游网络关注度的时空特征以及影响因素进行了实证分析并得到了相关的结论[7],Zhang等也做了类似研究[8]。这些研究表明网络搜索数据能显著提高模型预测精度,预测具有时效性,但主要集中在游客流量预测以及旅游网络关注度方面,对酒店需求预测研究甚少,在国内还没有相关文献对酒店入住率进行研究。本文拟扩展该方法在酒店需求预测中的应用。
虽然网络搜索数据被成功应用于旅游需求预测领域,但所使用的模型主要为经典时间序列或经济计量等线性模型。由于旅游需求是一个复杂的非线性系统,因此传统的预测技术难以对其进行充分的刻画,需寻求更为有效的预测工具。ANN具有良好的非线性预测能力,但受限于训练过程复杂,容易陷入局部最优以及对样本容量要求较大等缺陷。作为一种基于统计学习理论的机器学习算法,支持向量回归(Support Vector Regression,SVR)具有很强的非线性预测能力,并且可以解决小样本预测问题。该模型已被成功应用于旅游需求预测[9]。研究结果表明SVR模型的预测能力优于传统的非线性模型。但利用SVR进行预测会遇到两个技术障碍:首先是对模型自由参数的选择问题,不恰当参数设置会对预测结果产生重要影响[10]。针对自由参数的选择,已有研究主要应用粒子群优化算法(PSO)等对SVR模型的三个自由参数进行调整。比如,陈荣等利用PSO调整SVR的参数,并构建模型对黄山景区客流量进行了预测[9];Gu等应用遗传算法(Genetic Algorithm,GA)调节SVR的参数,并建立模型对房价进行了预测[11]。然而,这些参数优化算法在某些情况下容易存在局部最优等风险。Yang提出蝙蝠算法(Bat Algorithm,BA),其主要思想来源于自然界的蝙蝠觅食的过程[12]。与PSO等算法的搜索机制相同,但BA拥有更强的随机性,因而具备更快的收敛速度、不易陷入局部最优以及鲁棒性强等优点。
为克服传统预测技术的局限性,本文建立BA-SVR@CSQ混合模型对北京星级酒店的月度平均入住率进行预测,其中引入的BA用于模型自由参数的优化,利用2011年1月到2017年4月的百度网络搜索数据(CSQ)作为SVR模型的输入集,“@”旨在强调利用消费者搜索数据构造预测模型的输入集。为验证该方法的有效性,将BA-SVR (仅利用酒店入住率的历史观测作为输入集)、PSO-SVR@CSQ、ANN@CSQ以及BA-SVR@T作为基准模型以进行预测对比,其中,“T”用于强调利用铁路客运量数据*交通流量数据主要包括飞机、铁路、轮船以及公路等客运量数据,但由于除铁路客运量以外的其它交通数据或其它交通数据的加权平均值与被预测变量之间没有显著的相关性,故本文仅选择铁路客运量数据进行分析。构造模型输入集,BA-SVR@T旨在利用交通流量以及入住率历史观测数据预测酒店入住率并对比不同来源数据的预测效果。
二、预测方法设计
(一)支持向量回归算法
Vapnik引入支持向量机(SVM)以解决分类问题,SVM是基于统计学习理论的一种新颖的机器学习算法[13]988-999。随着ε(不敏感损失函数)的引入,回归版本的SVM即SVR被用于非线性回归预测问题[14]。SVR的本质是求解一个带约束的二次规划问题并提供全局最优解,其基本原理概括如下:
给定数据集:(xi,yi),yi∈R,xi∈Rn(i=1,2,…,N),其中xi表示输入向量,yi为与xi相对应的输出值。定义非线性映射φ:Rn→F,通过该映射,数据集xi被映射到高维特征空间F,在该特征空间理论上存在一个线性函数f(SVR函数),它描绘了xi与yi之间的非线性关系:
f(x)=ωTφ(x)+b
(1)
其中,f(x)为预测值,系数ω和b通过最小化正则风险函数获得:
(2)
满足如下约束条件:
(3)
其中,式(2)等号右边第一项表示Euclidean范数,控制模型的复杂度,第二项表示经验风险,该项利用ε不敏感损失函数惩罚训练误差,C用来折中模型的复杂度和经验风险[14]。式(3)中ζ与ζ*表示正的松弛变量,用来保证解的存在,ε用来度量不敏感损失函数。
将上述问题转化为对偶问题并求解一个二次规划问题,则线性函数f(x)可以表示为:
(4)
其中,拉格朗日乘子β和β*由求解二次规划问题确定,K(xi,x)表示SVR所使用的核函数,任何满足Mercer’s定理的函数均可作为SVR的核函数[14],本文采用最为常用的高斯径向基(RBF)核。因为核宽带、不敏感损失函数以及折中系数需要用户进行调整,因此要求求解一个三维的优化问题,本文利用蝙蝠算法对模型的这些自由参数进行优化。
(二)蝙蝠算法基本原理
BA由Yang提出,该算法综合了其它启发式智能算法的优点,其思想来源于自然界的蝙蝠觅食的行为[12,15]。由于BA具有收敛速度快、易于实现、结构简单,易获得全局最优解以及鲁棒性好等优点[15],使得该算法在多个学科和工程领域得到了广泛的应用。比如,Yang应用BA解决了一些工程优化问题,与其它优化技术相比,得到了令人满意的结果[15]。下面简要概括BA的原理,具体细节及相关假设可参考Yang。
蝙蝠采用声呐技术搜索食物目标并且对前方的障碍物进行有效的躲避,同时利用回声定位的声学原理来调整发声频率以判断所捕食物的大小,并通过回声的变化情况以探测目标物体的方向、距离、大小以及速度等,从而准确地飞行和捕食。Yang根据蝙蝠的这种生活习性以及目标优化问题提出了蝙蝠算法,具体而言,在n维搜索空间,蝙蝠的速度、位置、响度和脉冲速率可以用下列方程表示:
fi=fmin+(fmax-fmin)β
(5)
υit=υit-1+(xit-x*)fi
(6)
xit=xit-1+υit
(7)
其中,向量β在[0,1]区间上服从均匀分布,x*表示当前全局最优解,fmin和fmax分别表示最小和最大频率,需根据具体问题进行设置。
局部搜索则是通过随机游走的方式迭代进行:
xnew=xold+εAt
(8)
其中,ε表示在[-1,1]闭区间上的一个随机数,At=〈Ait〉表示所有蝙蝠在第t次迭代时间段的平均噪声,蝙蝠的音量Ai和脉冲发生率ri则通过式(9)进行更新:
Ait+1=αAit,rit+1=ri0[1-exp(-θt)]
(9)
对任意的0<α<1,θ>0,简单计算可以得到式(10):
Ait→0,rit→ri0,t→
(10)
其中,α和θ均为待定常数。当运用BA求解优化问题时,必须预先对BA自身的参数进行设置,这些参数包括:蝙蝠的数量N,A0,r0,α,θ,fmin,fmax以及随机游走步长λ。本文采用Taguchi方法对BA的参数进行设置[16]。
(三)BA-SVR@CSQ预测程序的构建
基于SVR和BA算法的基本原理,本文混合模型的预测可以通过以下步骤实现:
步骤1:BA参数的确定。在利用BA对SVR模型参数优化前,需对BA的若干参数进行设置,本文采用Taguchi法对其进行设置,该方法简化了实验的过程,简单易行。
步骤2:蝙蝠种群初始化。为获得SVR的最优参数集,我们必须对种群进行初始化,而种群被假定随机分布在整个搜索空间上,故本文需优化SVR的3个超参数。
步骤3:搜索新解。在该过程中,蝙蝠利用自身所处的具体位置和速度循环计算,从而搜索到最优解。
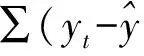
步骤5:停止迭代准则的判断。搜索新解和适应度评估两个步骤将会持续迭代,直至进化的代数与用户事先规定的迭代次数相等为止,同时在迭代过程停止时适应度曲线收敛,此时获得模型的最优解,然后将其带入SVR模型,并在测试集上进行预测实验。具体预测流程图见图1。
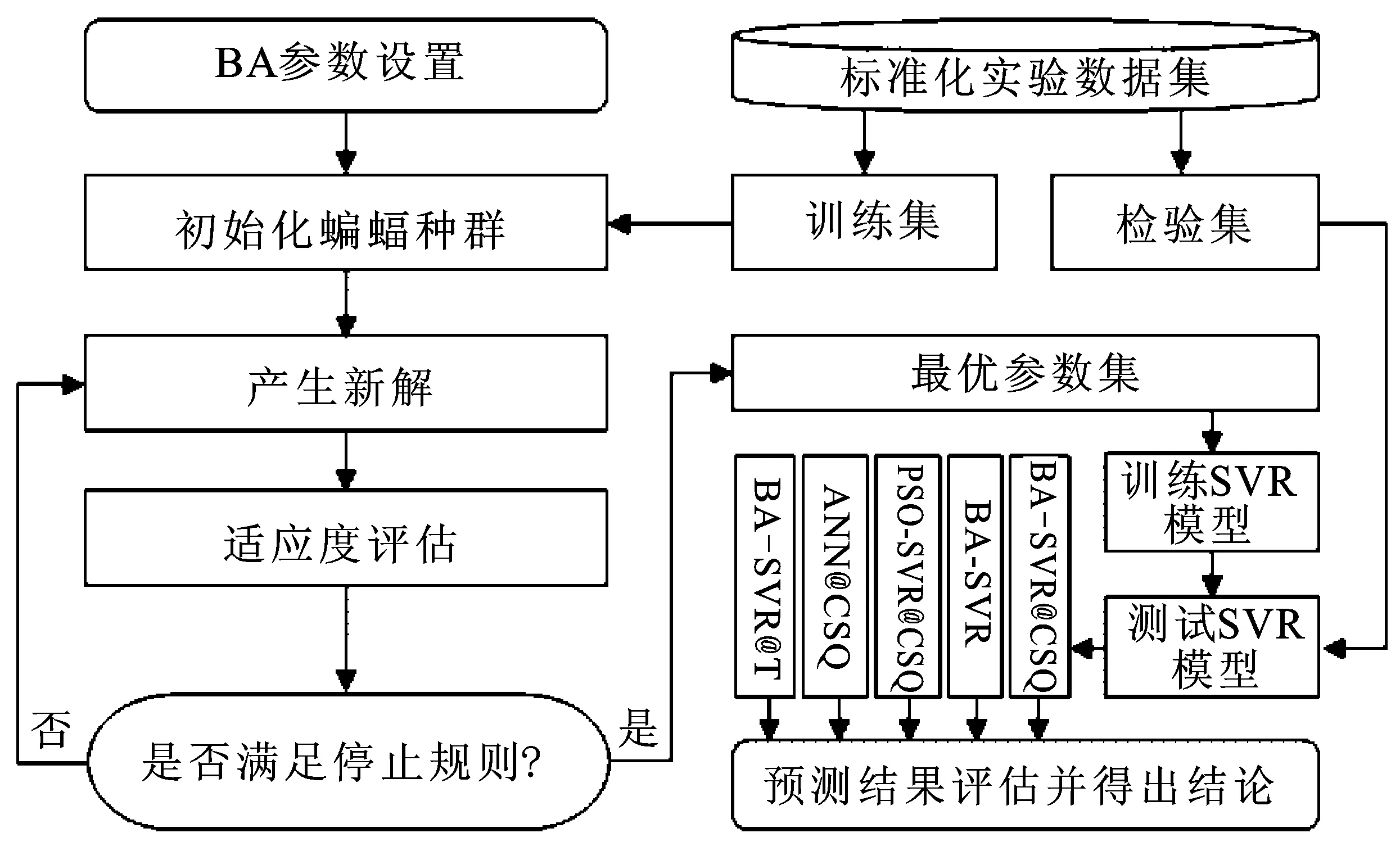
图1 BA-SVR@CSQ预测流程图
三、实证检验
(一)数据来源与模型输入集构造
由于酒店入住率可真实反映酒店接待客流量以及客房的利用情况,为证实引入方法的有效性,本文以北京为例,对北京市星级酒店月度平均入住率进行预测。北京是全球拥有世界遗产最多的城市,交通便捷,其旅游业已取得巨大的发展。据北京市统计局数据显示,2015年1-11月北京星级酒店收入合计2 358 819万元,同比增长1.4%;接待住宿人数18 515 974万人,同比增长3.9%.
星级酒店入住率以及铁路客运量数据来源于万得(wind)资讯,数据收集的时间范围为2011年1月至2017年4月。网络搜索数据来源于百度指数(http://index.baidu.com/),它是由百度提供的一项关键词免费查询服务,呈现了2011年1月至今的日度或周度整体趋势数据。
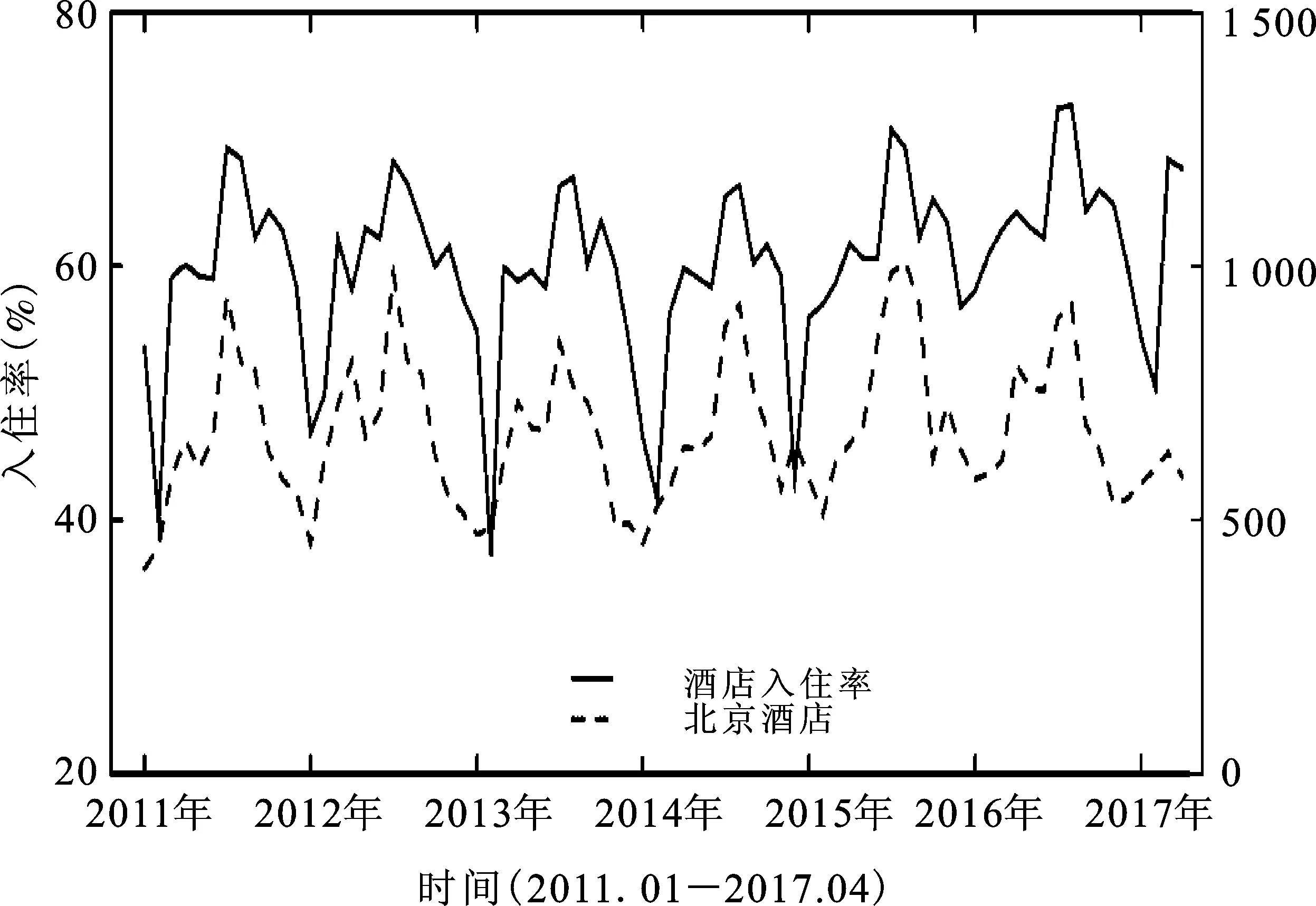
图2 关键词“北京酒店”与被预测变量趋势图
图2直观显示了 “北京酒店”这一关键词与被预测变量“酒店入住率”之间的趋势,可以看出两条曲线的波动特征极为相似,表现出较强的联动性和相关性,并且该关键词的波动时间一定程度上领先于酒店入住率变量。酒店入住率,在每年表现出相似的“凸”字型波动,在每年的7—8月份达到峰值,在春节左右回落到谷值。这是由于每年的7—8月为暑假,8月末为开学时间,这段时期大量游客流向北京市区,客流剧增,造成酒店入住率达到最高;而到了春节左右,大量务工人员和城市居民返乡,大量游客流出北京市区,造成市区短时间内客流骤减,从而酒店入住率达到最低。由于受其它季节性和随机性等因素影响,在每个周期内还出现小的峰值和谷值,但每个周期的波动特征又不尽相同。因此,本文假定与北京旅游相关的某些信息搜索能有效预测酒店入住率,并提高模型的预测能力。
网络搜索数据反映了游客潜在的旅游需求,尽管个别数据本身存在一定的缺陷,存在较大的噪声,不妨碍利用统计的方法找出关键词变量与被预测变量之间的相关性并证实该类数据对预测的有效性。由于与被预测变量相关的关键词并不唯一,如何从中甄别出最具预测力的预测变量是需要解决的关键问题。本文根据如下步骤对网络搜索数据进行获取与筛选:
1.基准关键词的确定。选择与北京旅游相关的基准关键词14个,这些基准关键词包括了与“吃”、“住”、“行”、“游”、“购”以及“娱”等旅游六要素相关的信息查询。
2.为避免遗漏重要关键词信息,循环查询与基准关键词相关的其它关键词信息,初步得到与北京旅游相关的关键词46个,并获取这些关键词的数据信息。由于被预测变量为月度数据,简单起见,将关键词变量(周度数据)按照平均加权求和的方式转换为月度数据。
3.预测变量的获取。以0.70为阈值,综合使用皮尔森交叉相关分析以及逐步回归的思想最终得到4个最具预测能力关键词。其中皮尔森交叉相关分析基于一种启发式算法,该算法能通过对时间序列进行统计分析,识别与时间序列相对应的不同滞后结构的潜在影响变量,这种方法能确保找出最具相关性的预测变量。但预测变量并非越多越好,关键词变量对模型的边际贡献是有限的,而逐步回归方法旨在确定最佳预测变量。最终所选择变量的相关性分析见表1。
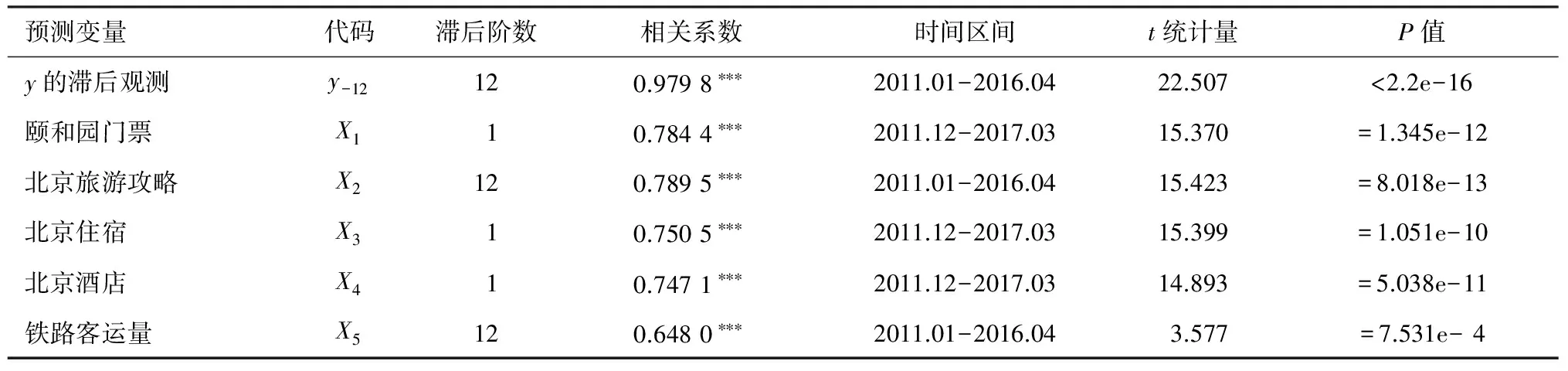
表1 所选预测变量与被预测变量相关分析表
注:***,**,*分别表示在1%,5%与10%水平显著,下同;所有时间区间已进行对齐处理;被预测变量y:酒店入住率 (2012.01-2017.04)
由表1可以看出,被预测变量与其12阶滞后变量之间存在显著的相关关系,相关系数达到了0.979 8,因此入住率的12阶滞后变量被选为预测变量;入住率与4个关键词的最优滞后变量之间也存在显著的相关关系。这些变量都反映了游客到北京旅游所关心的与旅游及住宿相关的问题。比如,他们会提前1个月在网络上对门票及住宿等相关问题进行查询,尽管消费者也查询了“北京酒店预订”等其它与北京旅游相关的潜在信息,考虑到变量选择的相关性以及预测能力,我们未能将其纳入到预测变量中来;上一年的铁路客运量与酒店入住率之间也存在显著的相关关系,相关系数为0.648 0。由于暑假和春节对入住率影响较大,引入季节虚拟变量dummy,当某月包含寒假或暑假时,取值为1,否则取值为0。基于以上分析,将实验数据集表示为:{yt-12,x1,t-1,x2,t-12,x3,t-1,x4,t-1,x5,t-12,dummy;yt},其中,{yt-12,x1,t-1,x2,t-12,x3,t-1,x4,t-1,x5,t-12,dummy}表示模型的输入集,yt为模型的输出变量,数据样本容量为64(滞后损失了12个数据点)。为消除不同变量的数量级对预测结果的影响,对实验数据集利用式(11)进行标准化处理以改善模型预测精度:
(11)
其中,xi为变量x的第i个数据点,xmin和xmax分别表示对应变量在样本区间的最小值和最大值。
预测后需对预测值进行标准化公式的逆变换N-1(xi)以获得实际的预测值。考虑到实验数据样本容量较小,为进行预测实验,将标准化后的实验数据分成训练集(前52个数据点)和检验集(最后12个数据点)两部分分别用于模型训练以及预测检验。
(二)模型预测性能度量
为验证BA-SVR@CSQ模型的预测能力,本文采用相关系数(R)、平均绝对误差比(MAPE)和均方根误差(RMSE)指标对预测误差进行评估,这些指标的定义如下:
(12)
(13)
(14)
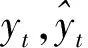
在3个性能度量指标中,MAPE和RMSE旨在衡量拟合值与期望值之间的偏差,其值愈小意味着模型的预测精度越高;R度量预测值与实际值之间的相关程度,其值越接近1意味着相关程度越大,预测性能越高。
(三)结果与讨论
根据预测程序,首先需要在训练集上训练模型以获得模型的最优参数,然后将训练的模型在检验集上进行预测实验。利用MATLAB 2015a进行实验,所建立BA-SVR@CSQ模型的最优参数集为:C=28.296,ε=0.991,δ=2.370,篇幅所限,其它模型最优参数集未能逐一列出。
将得到的最优模型在检验集上进行预测,各个模型预测结果见表2,该表显示在12个月的预测值中,BA-SVR@CSQ和PSO-SVR@CSQ模型的最优预测值(标记为黑体)均为4个月,ANN@CSQ为2个月,而BA-SVR与BA-SVR@T均1个月。预测值暗示本文构建的预测方法具有更好的预测效果;BA-SVR由于仅使用了入住率的滞后观测作为模型的输入集,使得预测能力最差,这证实了引入网络搜索数据能提高模型的预测能力;PSO-SVR@CSQ也具有很好的预测能力;而ANN@CSQ模型虽使用了网络搜索数据作为输入集并且具有良好的非线性预测能力,但由于ANN不适用于小样本预测问题,所以预测性能差强人意;BA-SVR@T基于铁路客运量数据进行预测,其预测能力与基于网络搜索数据模型的预测能力有很大差距。图3更为直观地显示出各个模型的预测曲线与实际曲线之间的偏差,可以看出BA-SVR@CSQ的拟合效果最好,具体预测性能是否具有差异还需从统计性能指标进行验证。
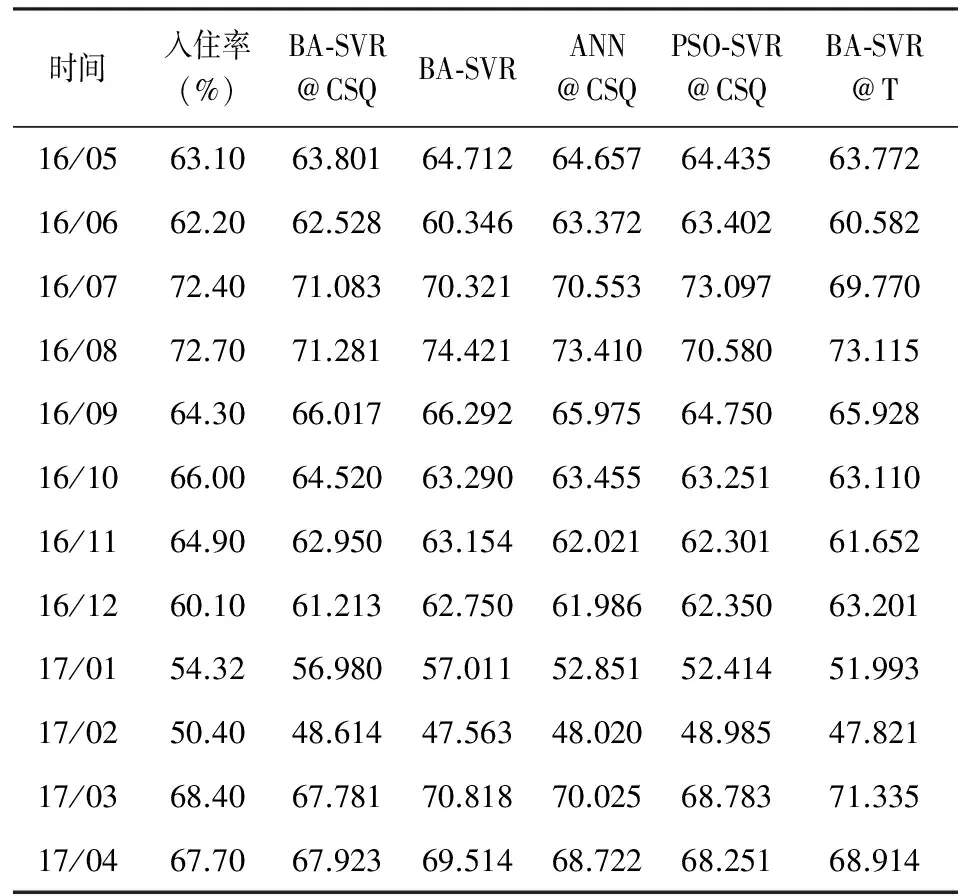
表2 不同模型预测结果对比表
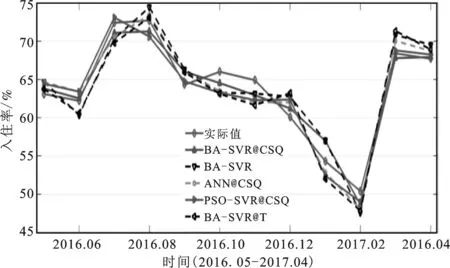
图3不同模型预测曲线对比图
为进一步对上述结论进行验证,基于预测结果的3个统计度量指标值见表3。从总体上看,3个度量指标值显示BA-SVR@CSQ模型预测性能最佳,其次是PSO-SVR@CSQ和ANN@CSQ,表现最差的仍然是BA-SVR模型。具体而言,平均绝对误差百分比和均方根误差值暗示BA-SVR@CSQ的拟合值与期望值之间具有最小偏差,从而预测精度最高,而没有利用网络搜索数据的BA-SVR模型预测偏离最大;与BA-SVR@CSQ相比,基于铁路客运量数据的BA-SVR@T与实际值的偏离程度更大。就相关系数R而言,BA-SVR@CSQ模型的预测结果与实际值相关程度最高,表现最差的仍为BA-SVR。
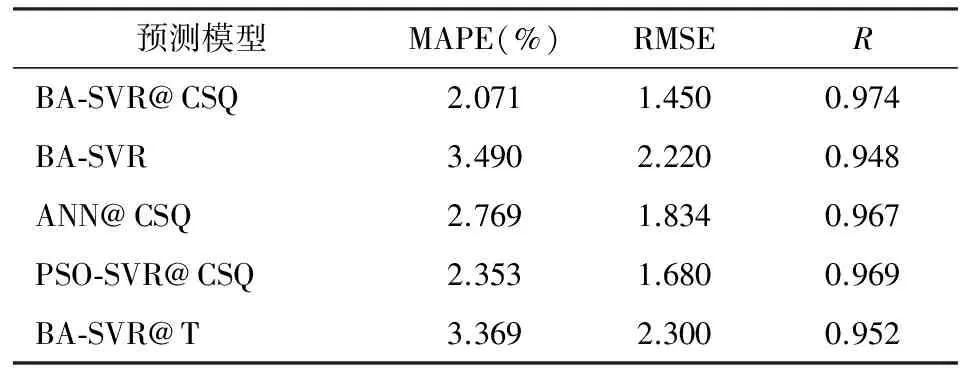
表3 不同预测模型的统计性能指标
上述基于预测结果的分析验证了所构建的BA-SVR@CSQ混合模型具有良好的预测性能,而网络搜索数据的引入提高了模型的预测精度,这与已有文献结论一致[6,8];同时证实了与PSO优化算法相比,BA不易陷入局部最优、更具鲁棒性强等优点;ANN虽然有较强的非线性预测能力,但在处理小样本数据预测方面表现较差;铁路客运量数据不具备网络搜索数据的一些优点,同时由于相关性等原因未能整合其它交通流量数据,导致BA-SVR@T模型的预测能力不如BA-SVR@CSQ。
四、结 论
随着信息技术的发展和互联网的普及,网络搜索数据在社会经济行为中的预测效果明显,它对消费者行为敏感,克服了传统预测变量存在难以获取、数据发布滞后以及对数据结构要求严格等缺陷。针对旅游需求曲线的非线性特征,本文建立BA-SVR@CSQ模型对北京星级酒店入住率进行预测,基于预测结果的统计性能指标,证实了网络搜索数据的引入能有效提高模型的预测精度,该模型是一种恰当的酒店入住率预测工具。
本文所建立模型具有良好的预测性能可归功于三方面原因。首先,SVR模型超参数的选择对预测精度有着重要的影响,而BA所具备的良好性质保证了预测模型优异的泛化能力,从而避免了诸如PSO和GA等算法的缺陷。因此,与基准模型PSO-SVR@CSQ相比,BA-SVR@CSQ预测更为精确。其次,就数据来源而言,与BA-SVR和BA-SVR@T模型不同,本文提出的预测方法充分利用了消费者信息搜索数据作为模型的输入集,这类数据能提供更为综合、实时的信息,从而有助于提高模型的预测能力。本文对预测变量的选择方法和数据标准化处理程序在一定程度上有助于提高模型的预测精度。
就实际应用而言,本文将网络搜索数据作为BA-SVR的输入集,结果显示能有效提高模型的预测能力,可将所构建预测技术推广到其它旅游目的地或旅游需求预测,例如将网络搜索数据引入到非线性预测模型,对景区旅游收入以及景区游客流量进行预测。预测结果可为相关行业提供必要的参考,对旅游相关部门的决策与管理起到十分重要的作用。在互联网环境下,相关管理部门也应重视与旅游要素相关的关键词数据的营销策略,并应用于旅游需求预测以提升市场竞争力。
受限于数据收集的困难,本文未能考虑其它来源的实验数据集。在将来的研究中,探索更具预测能力的数据来源,利用其它地区的酒店行业相关数据对本文建立的方法进行检验以及开发更具预测能力的预测工具是进一步努力的方向。
[1] Weatherford L R,Kimes S E.A Comparisonof Forecasting Methods for Hotel Revenue Management[J].International Journal of Forecasting,2003,19(3).
[2] Song H,Li G.Tourism Demand Modelling and Forecasting:A Review of Recent Research[J].Tourism Management,2008,29 (2).
[3] Fodness D,Murray B.A Typology of Tourist Information Search Strategies[J].Journal of Travel Research,1998,37(2).
[4] Choi H,Varian H.Predicting Present with Google Trends[J].Economic Record,2012,88(1).
[5] Yang X,Pan B,James A,et al.Forecasting Chinese Tourist Volume with Search Engine Data[J].Tourism Management,2015(46).
[6] 王炼,贾建明.基于网络信息搜索的旅游需求预测——来自黄金周的证据[J].系统管理学报,2014,23(3).
[7] 李霞,曲洪建.邮轮旅游网络关注度的时空特征和影响因素——基于百度指数的研究[J].统计与信息论坛,2016,31(4).
[8] Zhang B R,Huang X K,Li N,et al.A Novel Hybrid Model for Tourist Volume Forecasting Incorporating Search Engine Data[J].Asia Pacific Journal of Tourism Research,2017,22(3).
[9] 陈荣,梁昌勇,陆文星,等.基于季节SVR-PSO的旅游客流量预测模型研究[J].系统工程理论与实践,2014,34(5).
[10] Andre J,Siarry P,Dognon T.An Improvement of the Standard Genetic Algorithm Fighting Premature Convergence in Continuous Optimization[J].Advances in Engineering Sortware,2001,32 (1).
[11] Gu J,Zhu M,Jiang L.Housing Price Forecasting Based on Genetic Algorithm and Support Vector Machine[J],Expert Syst,2011,38 (4).
[12] Yang X S.Nature Inspired Cooperative Strategies for Optimization[R].Berlin Heidelberg:Springer,2010.
[13] Vapnik V.The Nature of Statistical Learning Theory [M].New York:Springer,1995.
[14] Drucker H,Burges C J C,Kaufman L,et al.Support Vector Regression Machines[J].Advances in Neural Information Processing Systems,1996,28(7).
[15] Yang X S.Bat Algorithm:A Novel Approach for Global Engineering Optimization[J].Engineering Computations,2012(5).
[16] Ghani J,Choudhury I,Hassan H.Application of Taguchi Method in the Optimization of End Milling Parameters[J].Journal of Materials Processing Technology,2004,145(1).

