ALMOST PERIODIC SOLUTION OF A NONAUTONOMOUS MODIFIED LESLIEGOWER PREDATOR-PREY MODEL WITH NONMONOTONIC FUNCTIONAL RESPONSE AND A PREY REFUGE∗†

Jinhuang Chen

(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)

1 Introduction

The traditional Leslie-Gower predator-prey model,which was proposed by Leslie([1]),which takes the form:

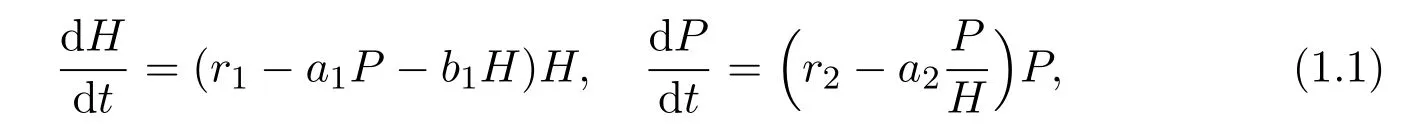
where H and P are the densities of prey species and the predator species at time t,respectively.A.Korobeinikov[2]showed the unique positive equilibrium of system(1.1)is globally stable.

Lian and Xu[3]proposed the following delayed Leslie-Gower model with nonmonotonic functional response:

By choosing the delay τ as a bifurcation parameter,the authors investigated the local asymptotic stability of the positive equilibrium and existence of local Hopf bifurcations.The supercritical stable Hopf bifurcations were also found by normal form theory.

With the aim of finding how the hunting delay affects the dynamics of the Leslie-Gower predator-prey model with nonmonotonic functional response,Jiao and Song[4]proposed the following model:

Such topics as the existence and local stability,global stability property of the positive equilibrium of the system were investigated.The authors also investigated the Hopf bifurcations of the system.In[5],the authors further investigated the dynamic behaviors of system(1.2)near the Bogdanov-Takens bifurcation point.By analyzing the characteristic equation associated with the non-hyperbolic equilibrium,the critical value of the delay inducing the Bogdanov-Takens bifurcation was obtained.They showed that the change of delay can result in heteroclinic orbit,homoclinic orbit and unstable limit cycle.

Yin et al[6]considered the spatial heterogeneity of the predators and preys distributions,and proposed a diffusive Leslie-Gower predator-prey system with nonmonotonic functional response:

The authors investigated the persistence of the model,the local and global stability of positive constant equilibrium and the Turing instability of the equilibrium.

On the other hand,more and more scholars have paid attention to the dynamic behaviors of the predator-prey system incorporating a prey refuge(see[7-10]).Chen et al[7]extended model(1.1)by incorporating a refuge protecting mH of the prey,

where m∈[0,1)is a constant,and proposed the following system:

where m∈[0,1)and ri,ai,i=1,2,b1are all positive constants.By constructing some suitable Lyapunov function,they showed that the unique positive equilibrium of the system is globally stable,consequently,prey refuge has no influence on the persistent property of the system.

Recently,Yue[8]proposed and studied the following modified Leslie-Gower predator-prey model with Holling-type II schemes and a prey refuge:

The author obtained a set of sufficient conditions which ensure the global attractivity of a positive equilibrium.

It brings to our attention that to this day,still no scholar propose the modified Leslie-Gower predator prey model with nonmonotonic functional response and a prey refuge.This motivates us to propose the following system:

where x(t)and y(t)denote the densities of the prey and predator species at time t,respectively;in this system,we incorporate a refuge protecting m(t)x of the prey,where m(t)∈[0,1),this leaves(1−m(t))x of the prey available to the predator.

Throughout this paper,we assume that:

(H1)ki(t),ci(t),ri(t),i=1,2,m(t),b1(t)are all continuous and strictly positive almost periodic functions defined on[0,+∞).

We consider(1.7)together with the following initial conditions

We mention here that the assumption of almost periodicity of the coefficients in(1.7)is a way of incorporating the time dependent variability of the environment,especially when the various components of the environment are periodic with not necessary commensurate periods(e.g.seasonal effects of weather,food supplies,mating habits,harvesting etc.).During the last decade,many scholars have investigated the almost periodic solution of the population dynamics,and some excellent results have been obtained,see[11-13]and the references therein.

The aim of this paper is to obtain a set of sufficient conditions which ensure the existence of a unique globally attractive positive almost periodic solution of system(1.7)with(1.8).

The rest of the paper is arranged as follows:In Section 2,we obtain sufficient conditions which guarantee the permanence of system(1.7).In Section 3,we obtain sufficient conditions which ensure the existence of a unique global attractive almost periodic solution of system(1.7).In Section 4,an example together with its numeric simulations illustrate the feasibility of the main results.We end this paper by a briefly discussion.

2 Permanence

For the rest of the paper,for a bounded continuous function g defined on R,let gLand gMbe defined as

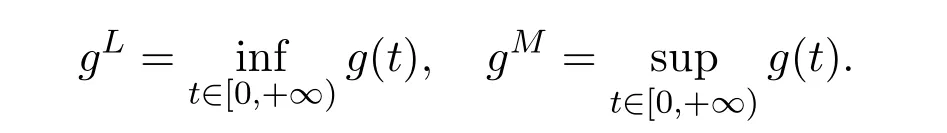
Lemma 2.1[14]If a＞0,b＞0 and˙x≥x(b−ax),when t≥0 and x(0)＞0,we have

If a＞0,b＞0 and˙x≤x(b−ax),when t≥0 and x(0)＞0,we have

Lemma 2.2The domain={(x,y)|x＞0,y＞0}is invariant with respect to(1.7).

ProofSince

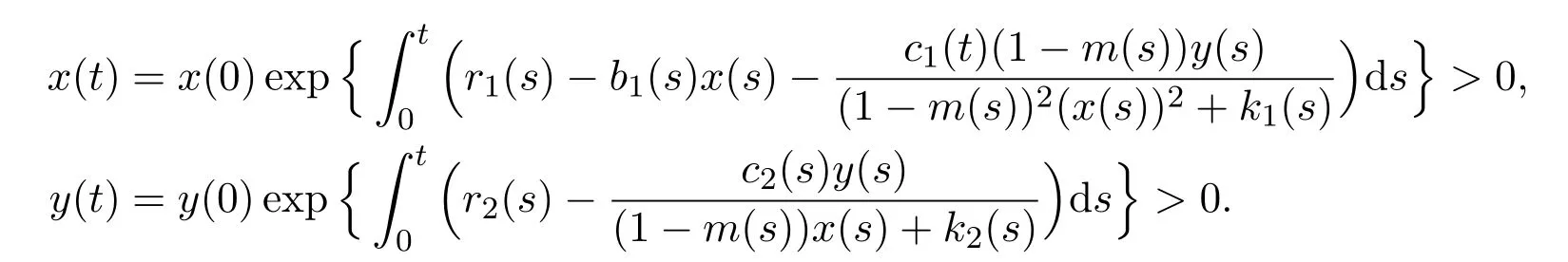
The assertion of the lemma follows immediately for all t∈[0,+∞).

Lemma 2.3Let(x(t),y(t))Tbe any solution of system(1.7)with(1.8),then

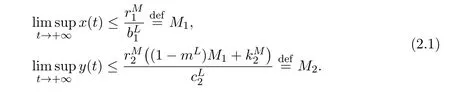
ProofLet(x(t),y(t))Tbe any solution of system(1.7)with(1.8).From the first equation of system(1.7),it follows that

Applying Lemma 2.1 to(2.2),it immediately follows that

For any positive constant ε ＞ 0 small enough,it follows from(2.2)that there exists a T1＞0 such that

For t＞T1,(2.4)together with the second equation of system(1.7)leads to

Applying Lemma 2.1 to(2.5),it immediately follows that

Set ε→ 0,then

This ends the proof of Lemma 2.3.

Lemma 2.4Let(x(t),y(t))Tbe any solution of system(1.7)with(1.8).Assume that

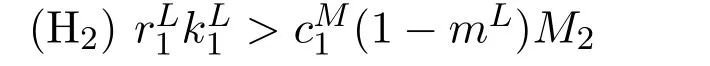
holds,then

ProofFor ε small enough,it follows from(2.1)that there exists a T2＞ T1such that

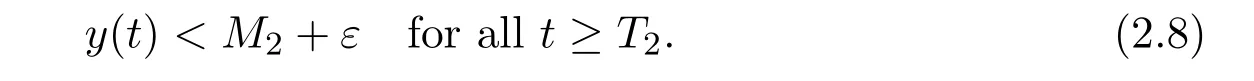
Let(x(t),y(t))Tbe any solution of system(1.7)with(1.8).For t＞T2,(2.8)together with the first equation of system(1.7)leads to

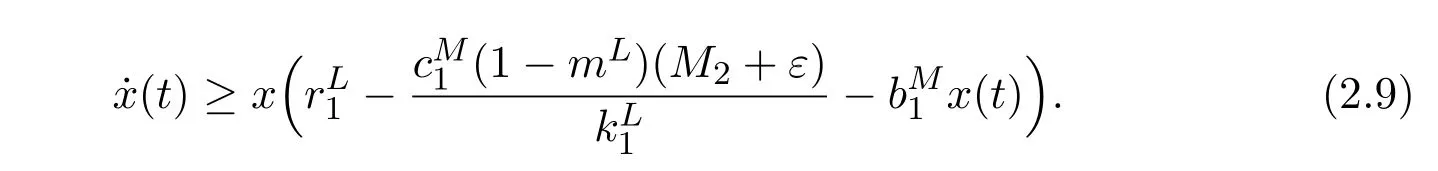
Applying Lemma 2.1 to(2.9),it immediately follows that

Set ε→ 0,then

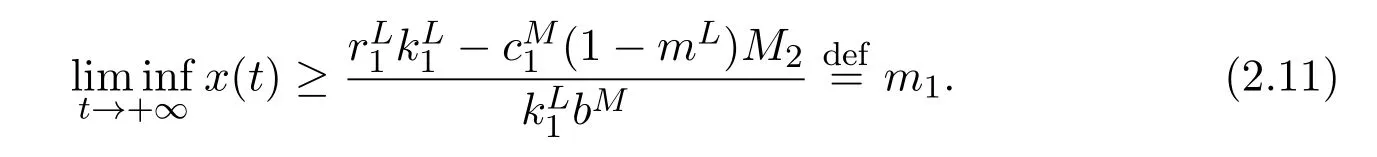
From the second equation of system(1.7),we have

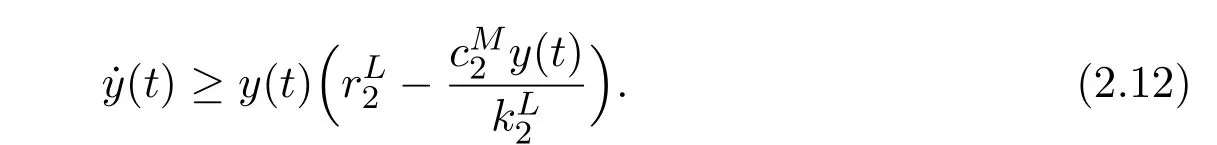
Apply Lemma 2.1 to(2.12),then

As a direct corollary of Lemmas 2.3 and 2.4,we have:

Theorem 2.1Under assumptions(H1)and(H2),system(1.7)with(1.8)is permanent.

Remark 2.1Noting that if m(t)is enough large,then condition(H2)always holds,and from Theorem 2.1,system(1.7)is permanent,which means that prey refuge could improve the change of the survival of prey species,and finally leads to the coexistence of the two species.

De fine

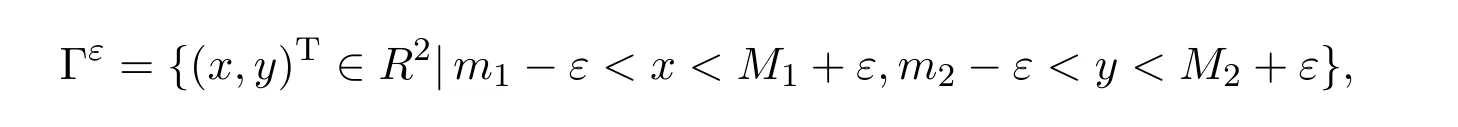
where ε＞ 0 is sufficiently small.By using(2.2),(2.5),(2.9)and(2.12),similarly to the analysis of Lemma 2.3 in[11],we have:

Theorem 2.2Under assumptions(H1)and(H2),the set Γεis invariant with respect to(1.7).

3 Extinction of Prey Species

The aim of this section is to obtain a set of sufficient conditions which ensure the extinction of the prey species,more precisely,we have the following result.Theorem 3.1Assume that

(H3)

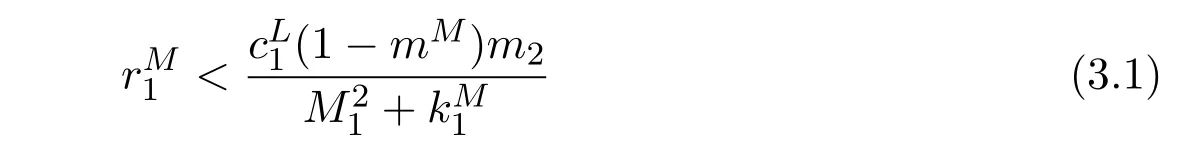
holds.Then the prey species will be driven to extinction.

Remark 3.1Condition(H3)shows that despite the refuge protect part of the prey species,if the net birth rate of the prey species is lower enough,then the prey species still be driven to extinction.

Proof of Theorem 3.1Condition(H3)implies that one could choose an ε＞ 0enough small such that

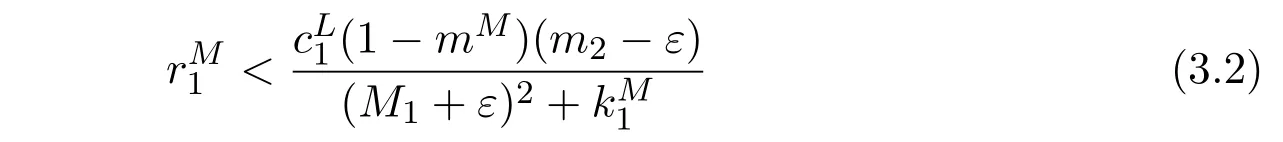
holds.For this ε,from the proof of Theorem 2.1,there exists an enough large T3＞T2such that for all t＞T3

Then,from the first equation of system(1.7),one has

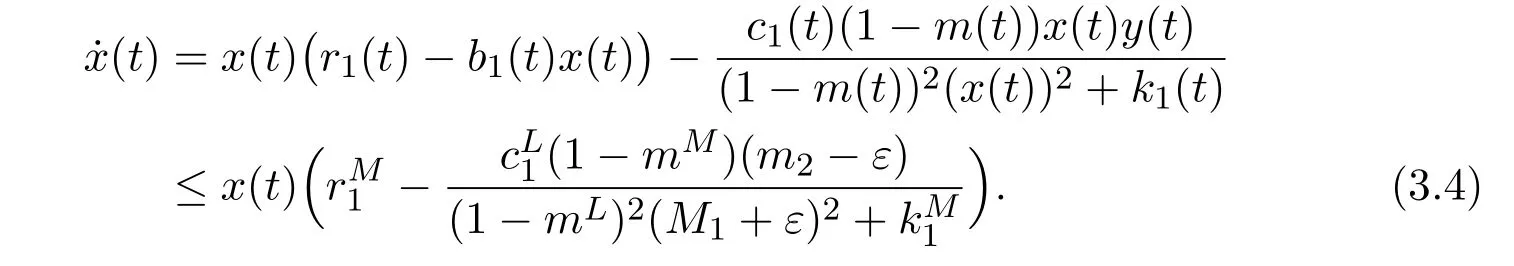
Thus,it immediately follows from(3.2)that

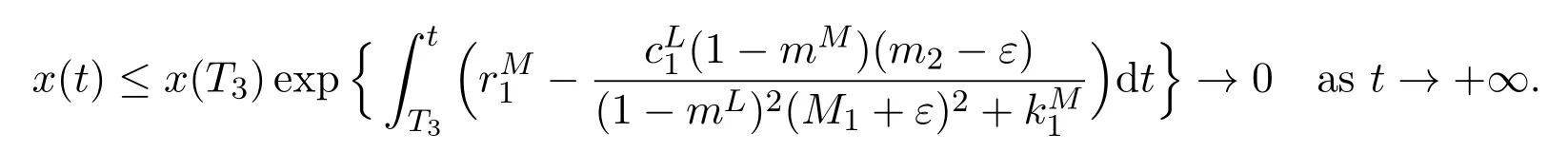
This ends the proof of Theorem 3.1.

4 Global Attractivity

Before we state the main result of this section,we introduce some notations.Set

Theorem 4.1In addition to(H1)-(H2),assume further that

then for any positive solutions(x(t),y(t))Tand(x∗(t),y∗(t))Tof system(1.7),one has

As a direct corollary of Theorem 4.1,we have:

Corollary 4.1In addition to(H1)-(H2),assume further that

then for any positive solutions(x(t),y(t))Tand(x∗(t),y∗(t))Tof system(1.7),one has

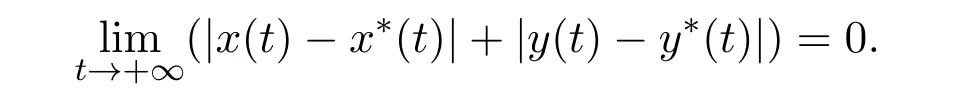
Remark 4.1Note that if m(t)is enough large,then inequalities(4.4)always holds,consequently,the predator and prey species could be coexistence in a stable state.This means that prey refuge has positive effect on the stability property of the system.

Proof of Theorem 4.1Condition(4.2)implies that there exists an enough small positive constant ε(without loss of generality,we may assume that ε＜{m1,m2})such that

For two arbitrary positive solutions(x(t),y(t))Tand(x∗(t),y∗(t))Tof system(1.7),for the above ε＞ 0,it follows from(2.1)and(2.7)that there exists an enough large T,such that for all t≥T

Now we let

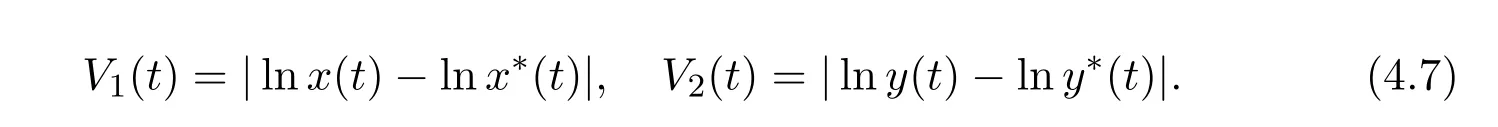
Then,by using(4.6),for t＞T,we have

Similarly,

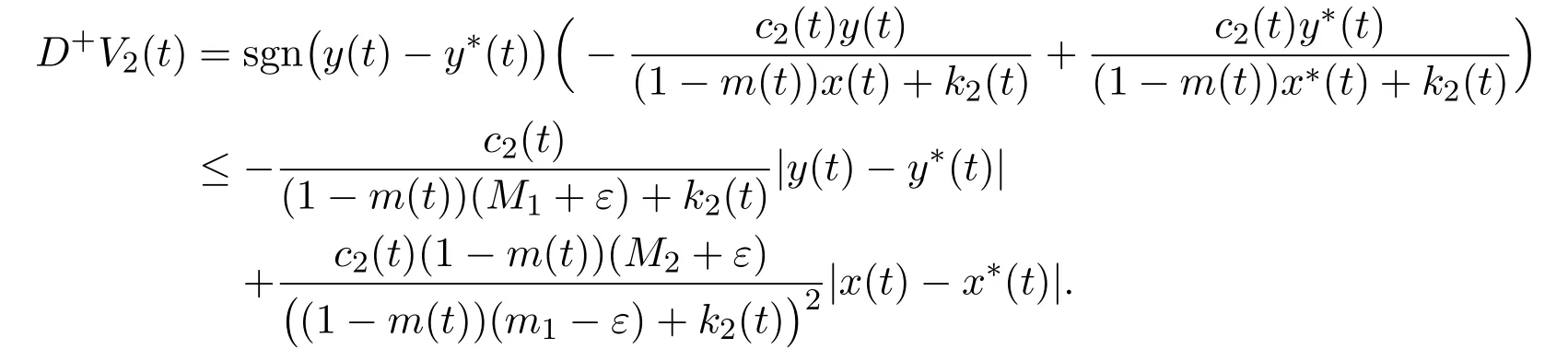
Now set

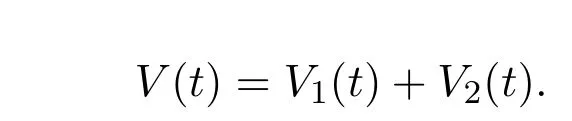
Then

Integrating both sides of(4.8)on interval[T,t),

It follows from(4.5)that

Therefore,V(t)is bounded on[T,+∞)and also

By Theorem 2.1,|x(t)−x∗(t)|,|y(t)−y∗(t)|are bounded on[T,+∞).On the other hand,it is easy to see that˙x(t),˙y(t),˙x1(t)and˙y1(t)are bounded for t≥T.Therefore,|x(t)− x∗(t)|,|y(t)− y∗(t)|are uniformly continuous on[T,+∞).By Barb˘alat lemma,one can conclude that

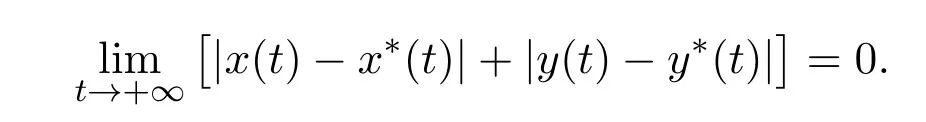
This ends the proof of the Theorem 4.1.

5 Almost Periodic Solution

This section deals with the almost periodic solution of system(1.7).

Let

then system(1.7)becomes

By the relationship of systems(5.1)and(1.7),corresponding to Theorem 2.2,one could easily obtain the following results.

Lemma 5.1Under assumptions(H1)and(H2),the setde fined by

is invariant with respect to(5.1).

It is obvious that if system(5.1)exists an almost periodic solution,then system(1.7)also exists a positive almost periodic solution.

Now we are in the position of stating the main results of this section:

Theorem 5.1In addition to assumptions(H1)and(H2),assume further that there exists aµ＞0 such that

where Ai(t),i=1,2 are de fined by(4.1),then system(1.7)admits a unique globally attractive strictly positive(componentwise)almost periodic solution(x(t),y(t)),t∈R.

ProofFor ε＞ 0 enough small,from(5.2)one could obtain that

where Ai(ε,t),i=1,2 are defined by(4.5)and(4.6).

We first shows that system(5.1)has a unique almost periodic solution that is uniformly asymptotically stable in

Consider the product system of system(5.1)

Consider a Lyapunov function defined on[0,+∞)××as follows

It then follows

where A=B=1.

In addition

Finally,calculate the right derivative D+V(t)of V(t)along the solutions of system(5.1),by using Lemma 3.2,similarly to the analysis of Theorem 2.1,by using(5.3),we can obtain:

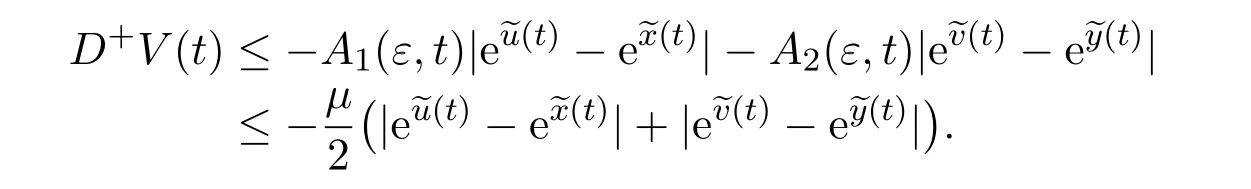
Note that

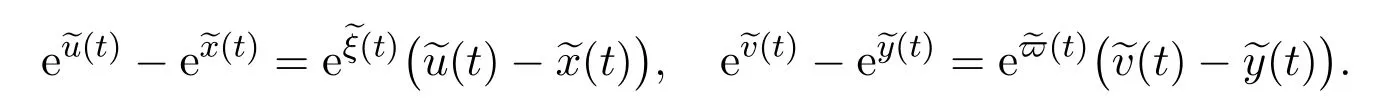
Then we have

where m=min{m1− ε,m2− ε}.Hence,the condition(3)of Lemma 5.1 is also satisfied.

The above analysis shows that all the conditions of Theorem 6.3 in[15]hold.Thus,system(5.1)has a unique almost periodic solutionwhich is uniformly asymptoticallystable in.Hence,system(1.7)has a unique positive almost periodic solution which is uniformly asymptotically stable in Γε.The global attractivity of the positive almost periodic solution of system(1.7)is a direct corollary of Theorem 4.1.The proof is completed.

6 Numeric Examples

Now let’s consider the following examples.

Example 6.1

One could easily verify the system satisfies the conditions of Corollary 4.1 and Theorem 5.1,then system(6.1)admits a unique globally attractive strictly positive(componentwise)almost periodic solution(x∗(t),y∗(t)),t∈ R.Numeric simulations(Figures 6.1,6.2)also support this finds.

Figure 1:Dynamic behavior of the first component x(t)of the solution(x(t),y(t))of system(6.1)with the initial conditions(x(0),y(0))=(1,1),(0.3,2),(0.2,2),(0.1,3)and(0.2,0.2),respectively.

Figure 2:Dynamic behavior of the second component y(t)of the solution(x(t),y(t))of system(6.1)with the initial conditions(x(0),y(0))=(1,1),(0.3,2),(0.2,2),(0.1,3)and(0.2,0.2),respectively.

Example 6.2

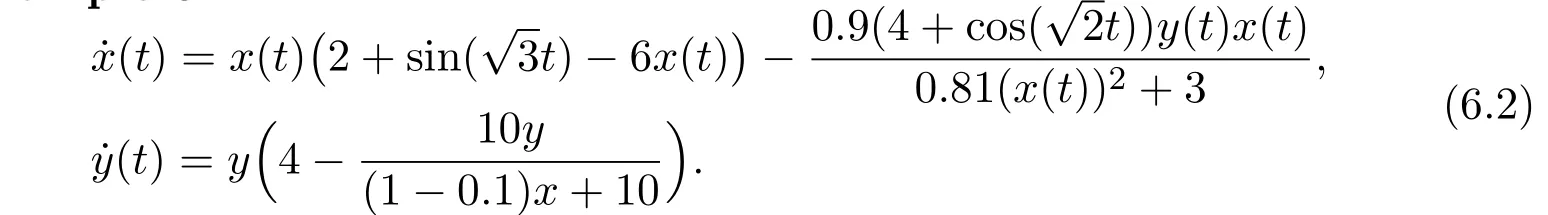
One could easily verify the system satisfies the conditions of Theorem 3.1,hence the prey species will be driven to extinction.Numeric simulations(Figure 6.3)also support this finds.

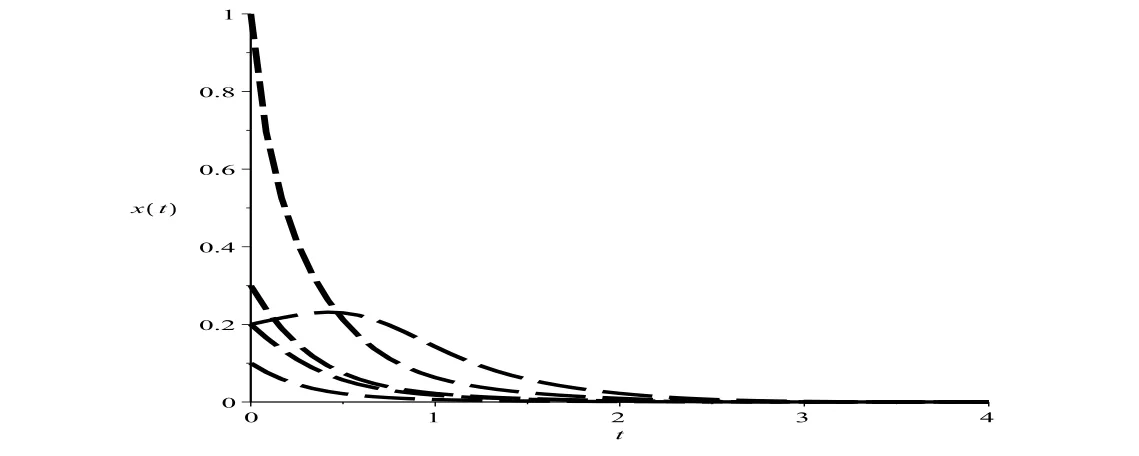
Figure 3:Dynamic behavior of the first component x(t)of the solution(x(t),y(t))of system(6.2)with the initial conditions(x(0),y(0))=(1,1),(0.3,2),(0.2,2),(0.1,3)and(0.2,0.2),respectively.

7 Conclusion

In this paper,stimulated by the works of Lian and Xu[3],Chen et al[7]and Yue[8],we propose a nonautonomous modified Leslie-Gower predator-prey system with nonmonotonic functional response and a prey refuge.We pay attention to the persistent and stability property of the system,as well as that of the existence of a unique globally attractive almost periodic solution.

One interesting finding is that for system(1.7),the prey refuge plays an important role on the persistent property of the system,One could always provide enough large prey refuge,such that two species could be coexist in a stable state.

We mention here that delay is one of the most important factor which could lead to the bifurcation of the system,and it seems interesting to study the almost periodic solution of the delayed nonautonomous modified Leslie-Gower predator-prey system with non-monotonic functional response and a prey refuge.We leave this for future investigation.

[1]P.H.Leslie,A stochastic model for studying the properties of certain biological systems by numerical methods,Biometrika,45:1-2(1958),16-31.

[2]A.Korobeinikov,A Lyapunov function for Leslie-Gower predator-prey models,Applied Mathematics Letters,14:6(2001),697-699.

[3]F.Lian and Y.Xu,Hopf bifurcation analysis of a predator-prey system with Holling type IV functional response and time delay,Applied Mathematics and Computation,215:4(2009),1484-1495.

[4]J.Jiang,Y.Song,Stability and bifurcation analysis of a delayed Leslie-Gower predatorprey system with nonmonotonic functional response,

AbstractAppl.Anal.,2013;2013:19 pages.Article ID 152459.

[5]J.Jiang,Y.L.Song,Delay induced Bogdanov-Takens bifurcation in a Leslie Gower predator prey model with nonmonotonic functional response,Communications in Nonlinear Science and Numerical Simulation,19:7(2014),2454-2465.

[6]H.W.Yin,J.X.Zhou,X.Y.Xiao,et al,Analysis of a diffusive Leslie-Gower predatorprey model with nonmonotonic functional response,Chaos,Solitons&Fractals,65(2014),51-61.

[7]F.D.Chen,L.J.Chen and X.D.Xie,On a Leslie-Gower predator-prey model incorporating a prey refuge,Nonlinear Analysis:Real World Applications,10:5(2009),2905-2908.

[8]Q.Yue,Dynamics of a modified Leslie-Gower predator-prey model with Holling-type II schemes and a prey refuge,SpringerPlus,5:1(2016),1-12.

[9]Y.Wu,F.Chen,W.Chen&Y.Lin,Dynamic behaviors of a nonautonomous discrete predator-prey system incorporating a prey refuge and Holling type II functional response,Discrete Dynamics in Nature&Society,2012(2012),1951-1965.

[10]L.J.Chen,F.D.Chen and L.J.Chen,Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a constant prey refuge,Nonlinear Analysis:Real World Applications,11:1(2010),246-252.

[11]F.D.Chen,C.L.Shi,Global attractivity in an almost periodic multi-species nonlinear ecological model,Applied Mathematics and Computation,180:1(2006),376-392.

[12]Z.Li,M.A.Chen,F.D.Chen,Almost periodic solutions of a discrete almost periodic logistic equation with delay,Applied Mathematics and Computation,232:1(2014),743-751.

[13]X.Xie,C.H.Zhang,X.X.Chen,J.Y.Chen,Almost periodic sequence solution of a discrete Hassell-Varley predator-prey system with feedback control,Applied Mathematics and Computation,268:1(2015),35-51.

[14]F.Chen,Z.Li,Y.J.Huang,Note on the permanence of a competitive system with in finite delay and feedback controls,Nonlinear Analysis:Real World Applications,8(2007),680-687.

[15]C.Y.He,Almost Periodic Differential Equations,Beijing:Higher Education Press,1992.(in Chinese)