空间众包中多类型任务的分配与调度方法
毛莺池,穆 超,包 威,李晓芳
(1.河海大学 计算机与信息学院,南京 211100; 2. 常州工学院 计算机信息工程学院,江苏 常州 213032)(*通信作者电子邮箱1813487536@qq.com)
0 引言
众包是指“一种把过去由专职员工执行的工作任务公开的Web平台以自愿的形式外包给非特定的解决方案提供者群体来完成的分布式问题求解模式”[1]。随着智能手机的普及,形成了众包新的发展方向——空间众包(Spatial Crowdsourcing)[2]。在众包中用户只要在线执行任务并提交任务的结果,而在空间众包中用户必须移动到任务指定的地点,才可以执行任务。空间众包被广泛应用于O2O(Online To Offline)、灾情监控、交通管理、物流管理和社交媒体等领域[3-6]。在空间众包领域中研究的核心问题[7]是空间任务分配与调度。现有的研究只是针对多类型任务的分配,并没有对任务的执行情况进行研究。本文以服务类O2O应用为例进行阐述,客人(任务发布者)发布需要的服务(任务),如维修电器、洗车等,众包平台为客人分配合适的服务人员(用户),服务人员到客人指定的地点提供服务。本研究需要规划路线,使得用户尽可能多地完成任务。本文的主要工作如下:
1)研究的对象是空间众包中的多类型任务,根据空间众包中任务的时空特性,在服务器端推送(Servers Assigned Task, SAT)模式下对任务进行分配,对贪婪分配算法进行改进,提出基于距离ε值分配(Distanceεbased Assignment,ε-DA)算法,为每个用户分配更多的专业匹配任务,并保持移动成本与其相差不大。
2)考虑任务的时空性,需要对执行任务的路线进行规划,以便在最短的时间内完成最多的任务。在任务分配基础上,采用分支定界思想(Branch and Bound Schedule, BBS)对任务进行调度,针对BBS运算速度较慢问题,提出最有前途分支启发式(Most Promising Branch Heuristic, MPBH)算法。
3)实验证明,提出的任务分配和调度方法能够提高任务完成的质量以及数量,并且在运行速度和精确性上有优势。
1 研究现状
众包中优化目标,可分为空间任务分配与任务调度问题。
1)任务分配问题。空间任务匹配问题通常转化为最大或最小加权二分图匹配问题[8],在静态模式下等价于空间匹配问题[9-10]的一种变种问题,而在动态模式下只能获取部分信息,利用部分二分图信息来进行匹配决策[11-15]。在任务分配问题中,优化目标是最大任务分配(Maximum Task Assignment, MTA)。在服务器推送(SAT)模式中,针对单一类型任务的任务分配[16-17],首先采用贪婪算法,尽量分配给用户maxT个任务;对Greedy算法改进,提出最小区域熵优先级策略,优先分配区域熵小的任务。然后,结合用户移动到任务地点所需的成本,提出最近距离优先级策略,优先分配距离用户最近的任务。针对复杂的任务[18],复杂任务分配是指将其所有子任务成功分配,才算分配一个复杂任务。在任务分配完成后,产生一个最初的任务序列,这时需要对任务序列进一步优化——任务调度。优化任务序列问题在静态情形下通常被规约为经典的旅行商问题[19]或定向问题[20],而在动态情形下每位众包参与者需要实时地决定新任务加入到其当前的任务规划之中[21]。通过合理规划路径,目标是实现最大任务调度(Maximum Task Scheduling, MTS)。在用户选择任务(Worker Selected Task, WST)模式中研究MTA[22],针对少量任务情况时,本文基于分支定界的思想去分配。当任务规模较大时,不断枚举任务组合耗时较大,提出最有前途分支启发式算法,根据节点的上界进行相应的修剪,提高分配的效率。
2)任务调度问题。然而,在现实众包应用中,对任务的调度往往不是单一地进行修剪,对于复杂的多类型任务,需要进行全局分配和局部调度[23]。文献[16-17]主要是对任务的分配的研究,并没有进一步对任务分配的质量进行研究;文献[18]研究的重点则是复杂任务的分解。文献[22]在WST模式下研究任务调度问题,会出现多个用户争夺同一任务情形,这时本文根据用户的移动成本和完成任务的质量[24-28]来选择最佳的用户;完成任务后,根据用户回答的准确性[29],赋给每个用户信誉分数,表示用户正确完成任务的概率。
综上,空间众包中核心问题是空间任务分配与任务调度。本文综合考虑这两方面,针对多类型任务进行研究,优化目标是最大化多类型任务完成的质量和数量。
2 多类型任务分配
2.1 问题模式
在SAT模式下,服务器对用户和任务信息有全局掌控,可以给每个用户分配附近的任务,最大限度地提高总体任务分配数量。任务发布者将任务发送给SC-server(众包服务器),在线用户将自己的信息报告给SC-server,SC-server根据这些用户属性和任务进行匹配,将任务分配给合适用户,如图1所示。

图1 空间众包组成
定义1 空间任务(Spatial Task)。一个空间任务t的形式为〈l,d,ei〉。其中:l表示该任务所在的位置;d表示任务t的截止时间;ei表示任务t的类型,下标表示任务的不同类型,多类型任务即所有任务的下标并不相同。本文忽略任务需要的执行时间。
定义2 用户(Worker)。一个用户w的形式为〈l,q,D,E〉。其中:l表示用户的当前位置,q表示用户最多能接受任务的数量,D表示用户区域,E表示用户具有的专业能力集合。
定义3 专业匹配(Expertise Match)[30]。一个匹配的形式为〈w,t〉,其中任务t要在用户的区域内。当用户具有完成任务t的专业能力,即ei∈E,称为专业匹配;若ei∉E,则称为非专业匹配。
如图2中,在用户w1的区域D1内,有任务t1、t2、t3、t4和t5,〈w1,t1〉匹配是专业匹配,因为用户w1具有两个专业能力{e1,e2},任务t1的类型为e1,e1∈{e1,e2}。而〈w1,t4〉匹配是非专业匹配,因为任务t4的类型为e3,e3∉{e1,e2}。
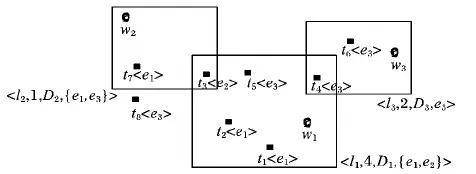
图2 一个用户任务分布实例
定义4 匹配分数(Score)[30]。对每个匹配〈w,t〉定义一个分数值Score(w,t),用于表示用户完成任务的质量。
显然将维修电器的任务分配给具有维修能力的用户,完成质量会比一般用户高,因此,专业匹配分数高于非专业匹配分数。本文不妨假设专业匹配分数为3,非专业匹配分数为1,在定理1中给出具体证明。如图2例中,Score(w1,t1)=3,Score(w1,t4)=1。
定义5 任务分配实例集(Task Assignment Instance Set)。在时间实例si时,在线用户集合为Wi={w1,w2,…,wn},可分配的任务集合为Ti={t1,t2,…,tm},所有匹配〈w,t〉的集合为任务分配实例集Ii。|Ii|代表在si时分配任务的数量。
定义6 移动成本(Travel Cost)。用欧氏距离d(wj,tk)计算表示用户wj和空间任务tk的移动成本。

2.2 解决问题思路
空间众包中任务和用户是动态的,用户可以随时在线或离线,任务也有时间限制,不能获得全局的用户和任务信息,在每个实例中,SC-server能够获得部分的任务和用户信息,只能在每个实例分配时进行局部优化,以达到最终的相对全局优化。现有文献[30]中贪婪算法思想是分配给每个用户尽可能多的任务,而且这些任务都是用户专业相匹配。若没有专业匹配时,用户只是选择一般的非专业匹配任务,不仅导致任务完成质量低,而且造成较高的移动成本。
本文首先将多类型任务分配转化为最大权值问题,利用二分图中的方法进行求解;然后,对基本的贪婪分配算法进行改进,结合空间任务的位置属性,提出基于距离ε值分配算法(ε-DA),尽可能多地分配专业匹配任务;其次,利用空间任务空间属性,在距离用户最近范围内选择ε个任务分配给用户,这样在任务调度时,没有合适的专业任务,可以选择非专业匹配任务,提高任务的完成数量,而且保证用户的移动成本在可接受范围内。
2.3 多类型任务分配转化为最大权值问题
文献[23]中将任务匹配转化为最大权值问题,研究的是单一类型任务,二分图的权值均为1。本文研究的是多类型任务分配问题,专业匹配分数为3,非专业匹配分数1,权值有所不同,将最大分数问题转换为在二分图中求最大权值问题。不妨先假设所有用户最多只能接受一个任务,在时间实例si时,在线用户集合为Wi={w1,w2,…,wn},可分配的任务集合为Ti={t1,t2,…,tm}。在无向图Gi=(V,E)中,如果任务tk在用户wj的区域范围内,则有边ej,k∈E连接这两个顶点。将每个边ej,k的权值赋予Score(wj,tk),因此,q=1时最大分数实例问题就转化为在带权二分图中求最大匹配问题了。
如图3所示,当每个用户的q=1时,图2中的实例转换的二分图,其中专业匹配的权值为3,非专业匹配的权值为1。
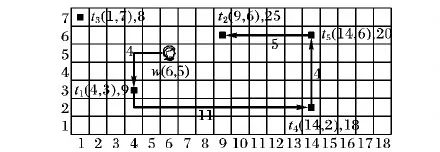
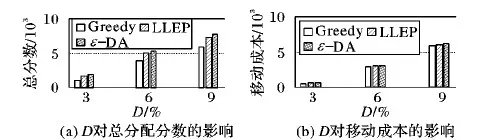
当每个用户至多能接受一个任务时,容易转化为二分图。当每个用户q=1时,该如何将任务分配问题转化为想要的二分图问题。不妨用N个逻辑用户来代替用户wj,这些逻辑用户只能接受一个任务,将q=1的二分图Gi转化Gi′。|Tj|表示在用户wj区域的任务数,当1 如图4所示,q=1时,用N个逻辑用户来代替用户wj,将Gi图转化为图Gi′,用3个逻辑用户表示用户w1,2个逻辑用户表示用户w3。 将MSA实例问题转化为在二分图中求最大权的问题,可利用KM(Kuhn-Munkras)算法解决该问题。KM算法的输入为一个矩阵|W|×|T|,矩阵中的值为对应的匹配分数。在每次实例分配时运用KM算法求出最大权值,得到每个用户的任务。如上述例中,求出分配给每个用户的任务为w1={t1,t2,t3}、w2={t7}、w3={t4,t6},得到的最大权值为3×6=18。 图4 q>1时二分图Gi′ 为了在用户最近距离内选择ε个任务分配给用户,这些任务与按照最大权值分配的任务不重合,在没有专业匹配时,将距离用户近的任务分配给用户,既可以减少用户的移动成本,又可以提高任务分配数量;在专业匹配距离较远时,用户通过调度执行任务,无法在截止时间内完成该专业匹配任务,此时可以选择去完成一些非专业匹配任务。例如通过最大权值二分图计算出w1={t1,t2,t3},虽然可以得到最大分配分数,但是,任务t3距离很远,若用户不能在截止时间内完成该任务,任务就失效。此时,不妨将距离较近的任务t5分配给用户w1,虽然不是专业匹配,但是用户也可以多完成一个任务,而且移动成本也较小,可以提高任务完成的数量。通过计算出每对匹配〈w,t〉的移动成本d(wj,tk),将这些任务按照d(wj,tk)降序排序,从中选择前ε个任务分配分配给用户。 基于距离ε值分配算法具体过程如算法1所示。 算法1 基于距离ε值分配(ε-DA)算法。 输入:用户集合Wi,任务集合Ti,ε值。 输出:Wi和Ti匹配的任务分配实例集Ii。 1) for eachsi 2) Construct a weighted bipartite graphGi′ byWiandTi 3) each weight given aScore(wj,tk) //给每个边赋予权值 4) Calculate the maximum weighted bipartite matching based on KM algorithm //利用KM算法计算最大权值匹配 5) Find the assignmentIibetweenWiandTi 6) for each workerwjinWi 7) Calculated(wj,tk) of each matching inwjregion by Euclidean distance //计算每个匹配的移动成本 8) Select the first someεtasks whosed(wj,tk) is minimum //选择移动成本小的ε个任务 9) UpdateIiby addingεtasks 在定义4中,假设专业匹配分数为3,非专业匹配分数为1,以下给出定理1及具体证明过程。 定理1 当专业匹配分数大于非专业匹配分数的两倍时,最大分数分配就是最大专业匹配。 可通过反证法证明。首先,假设每个用户最多能接受任务的数量q=1,MSA问题的最优解为Mmax。如果在Mmax中存在一个未分配的专业匹配〈w,t〉,并且w和t不在其他专业匹配中,为了提高总分数,最多可以用两个非专业匹配替换〈w,t〉。相反,若在Mmax中不存在未分配的专业匹配,那么在Mmax中专业匹配数量已是最大化。所以,当q=1且专业匹配分数大于非专业匹配分数的两倍时,最大分数匹配就是最大专业匹配。当量q>1时,可通过2.3节中原理分解为n个q=1的逻辑用户,同理可证明。 基于距离ε值分配算法的复杂度主要在于计算二分图中最大权值(第4)行),利用KM算法计算最大权值,时间复杂度可降低到O(n3)。选择距离最小的前ε个任务(第6)~9)行),时间复杂度为O(n2),因此基于距离ε值分配算法的复杂度为O(n3)。与贪婪分配算法相比,可忽略不计增加的时间代价O(n2)。 在上述任务分配过程中,虽然任务分配完成,但并不一定是最优序列,这时,需要对当前任务序列进行调度,使得任务序列中,用户在截止时间前以最短距离完成最多的任务。本文假设用户到达任务位置便完成该任务,不考虑任务的具体执行时间。 如图5所示,一个任务调度实例,将用户和任务分布在网格中,用户每移动1个网格耗费1个时间单位,用户w位于(6,5)处,假设该用户只具备美发专业能力,最大能接受数量为4。每个任务如定义1中给出的截止时间,例如任务t1的截止时间为9。分配给用户5个任务,将按照任务的截止时间合理规划任务执行次序。除了任务t2不是美发类服务,即非专业匹配任务;其他4个任务都是美发类服务,即专业匹配任务。 图5 一个任务调度实例 图6中展示了基于分支定界最大分数调度的主要思想:用户节点是树的根节点,在每一层中根据候选集合扩展分支,并依据上下界进行排序,不断递归直到找到一个可行的解决方案。当回溯到上一级时,若一个分支的上界小于当前最好解决方案或其他分支的下界,则修剪掉该分支。 3.1.1 候选任务集 对搜索树的每个节点,候选任务集是指在下一层中有希望被扩展节点的集合。例如,图6中的搜索树,在第一层的任务t5节点,初始时它有4个分支{t1,t3,t4,t2},但是只有任务t4和t2节点是有希望被扩展的节点,因为在用户完成t5后,已经过了任务t1和t3的截止时间,即任务t1和t3已失效。如果能够知道每个节点的候选任务集,那么只需要扩展这些较小的任务集合,不必盲目地搜索所有分支。为了计算每个节点的候选任务集,需要遍历其父节点的候选任务集合,并要保证可以在截至时间内完成任务。算法2是计算候选集的伪代码。 算法2 计算候选任务集CalculateCand(R,cand_R,t)。 输入:当前任务序列R,当前候选集合cand_R,t∈cand_R是将被扩展的任务。 输出:任务节点t候选集合cand_Rt。 1) GetcurTaskand its arriving timecurTimeofR 2) cand_Rt← ∅ 3) for each taskt′∈cand_R,t′≠tdo 4) ifcurTime+c(t,t′)≤d(t′) then //检查候选集中任务能否在截止时间内完成 5) Returncand_Rt 3.1.2 修剪策略 可以从候选集合中获取该节点的上界,上界代表在该分支下能够获得的最大调度分数,通过上界对搜索树进行修剪。以下给出节点R的上界ub_R计算公式: 定理2 假设知道当前最优解的分数为curMax和当前分支节点R,若R的上界小于最优解分数,即ub_R≤curMax,则可以将分支R修剪掉。 通过这个定理可知,节点的curMax越大,则修剪能力越强。如果能事先知道最优解的分数curMax,那么可修剪掉更多的分支,然后找出最优解中的调度次序;但由于实际情况中,并不能提前预知最优解分数,因此按照上界的降序排列,优先访问上界大的。 虽然基于分定定界思想的调度策略能够得到精确的任务执行次序,但是其时间和空间复杂度按照指数增长,难以适应真实的空间众包应用对实时性的要求。在本节提出基于距离最近的算法——最有前途分支启发式(MPBH)算法,在规定时间内完成指定任务。 最有前途分支启发式算法是在分支定界法基础上进行改进,通过不断迭代选择最有前途的分支(即在同一层中该分支节点具有最大的上限),选择一个最大上限的分支,并一直按照这个分支搜索下去,只需要找到一个候选任务序列即停止。具体步骤如算法3所示。 算法3 最有前途分支启发式算法。 输入:已分配的任务集合S和用户w。 输出:任务调度序列R。 1) R← ∅ 2) cand_Rt←S 3) whilecand_Ris not empty do 4) for each taskt∈cand_Rdo 5) cand_Rt←CalculateCand(R,cand_R,t) 6) Calculateub_Rt 7) end for 8) Sortcand_Rin descending order ofub_Rt, prune branches based onub 9) t← task with the largestubincand_R //选择上限最大的分支节点 10) R←R∪{t} 11) cand_R←cand_Rt 12) end while 13) returnR 对于上面的算法分析:相对于精确的分支定界思想调度策略,最有前途分支近似算法的复杂度要小得多,只需要搜索一个最优希望的分支即可,因此,空间复杂度为O(n),在每次候选集的选择中,都要选择一个上界更大的,所以时间复杂度在最坏情况下为O(n2)。 为了观察多类型任务分配与调度方法的执行效率,本文通过Matlab仿真平台进行仿真实验。 实验分别在真实数据和人工合成数据下进行。对于人工合成数据的生成,任务的截止时间d生成如下:从用户的位置,贪婪地选择下一个距离最近的一组任务组成一个任务序列,计算总的移动成本作为截止时间上界du(下界dl=du-0.1)。任务截止时间从均匀分布[dl,du]中产生,基本上范围[dl,du]确定可以完成的任务的百分比,较小的范围意味着任务的期限更紧。实验中人工合成数据,如表1,其中W/T表示对于一个给定的任务,用户区域包含该任务的平均用户数量。 表1 人工合成实验数据 对于真实数据,从现有的基于地理位置应用平台Yelp[31]中导出一些数据,2014年10月的数据。假设商户作为空间任务,Yelp中的用户作为空间众包参与者,用户点评一个商户就相当于在商户位置完成一个空间任务。商户的类别就是任务类型,用户具有的专业技能从这些任务类型中随机分配。任务最后期限是点评的完成时间,每个任务的处理时间是5 min。真实数据具体如表2所示。 表2 真实实验数据 实验中将现有的贪婪分配(Greedy)算法、最小区域熵优先(Least Location Entropy Priority, LLEP)算法与本文提出的基于距离ε值分配(ε-DA)算法进行比较,分别从三个维度比较分配算法的性能,包括总的分配分数、专业匹配任务数以及移动成本,对于每个实验跑50例,并报告结果的平均值。 4.2.1 关于ε值的讨论 ε值对ε-DA算法的影响如图7所示:随着ε值的增加,总分数和专业匹配任务数也增长。在ε≤10时增长较快,因为随着ε值增加,有一部分距离较近的专业匹配任务得到分配,使得分数增加较快;在ε>10时增长较缓慢,因为大部分任务分配出去了,剩余的专业匹配任务越来越少。随着ε值的增加,移动成本也在增长:在ε≤10时增长缓慢,是由于多选择的这部分任务距离用户较近,所以对移动成本影响不大;但是当ε>10时,移动成本增加较快,因为距离较远的任务也被分配了,使得总的移动成本不断增加,而且增速较快。由此看见,合适的ε值对总分数、专业匹配任务数以及移动成本影响较大,合理的ε取值很重要。 4.2.2 基于人工合成数据的实验 分别从任务规模W/T和用户区域约束条件D,验证对算法性能的影响。实验中ε值默认为10。 1)参数W/T的影响。实验结果如图8所示,图8(a)、(b)中,随着W/T变大,总分数和专业匹配分数都增加,因为随着W/T变大,可以匹配任务的用户越来越多。图8(a)中,实验结果表明,ε-DA算法比Greedy算法以及LLEP算法在总分配分数上表现得更好,其中比Greedy算法提升了接近30%,是由于ε-DA算法每次多选取部分任务,以获得较高的总的匹配分数。图8(b)中,ε-DA算法比Greedy算法以及LLEP算法获得更多的专业匹配任务。图8(c)中,虽然ε-DA算法每次多选取了部分任务,但是移动成本并没有增加过多,原因是多选择的这部分任务是距离用户最近的。而LLEP算法优先选择处于稀疏区域的任务,每次移动成本均较大。由此可见,随着W/T增加,ε-DA算法能够提高总的匹配分数,即在最大分数分配上表现得最好,能够获得更多的专业匹配任务,并且维持移动成本较小幅度的增加。 2)用户区域约束条件D的影响。用户有两个约束条件:最大能接受任务数q和用户区域范围D,两个约束条件相似,只列出约束条件D的影响。实验结果如图9中所示,在图9(a)中,随着用户区域范围D扩大,总的分配分数也增加,在图9(b)中,随着用户区域范围D扩大,移动成本也增加,是由于范围D扩大,距离较远的任务也能被分配出去,导致移动成本增加。由此可见,相对其他算法,随着范围D的扩大,ε-DA可以提高总的分配分数,同时移动成本并未剧烈增加。 图7 ε对3种约束条件的影响 图8 W/T对3种约束条件的影响 图9 D对两种约束条件的影响 4.2.3 基于真实数据的实验 在真实数据中对算法的性能进行测试,将本文提出的ε-DA算法、Greedy算法与LLEP算法进行比较。如图10所示,对比当W/T=50时3种算法的表现。从图10(a)~(b)实验结果表明,ε-DA算法在总分配分数上和专业匹配数上均比Greedy算法和LLEP算法表现得好,在专业匹配数上,ε-DA算法比Greedy算法提高了35%,比LLEP算法提高了11%。移动成本ε-DA算法比Greedy算法增加了9%,比LLEP算法减小7%。 本文对已有的工作深入研究,从空间众包中任务的多样性入手,根据空间任务的时空属性,在贪婪分配算法基础上进行改进,提出基于距离ε值分配算法,为任务调度提供合适的任务。采用分支定界思想对任务进行路径规划,在此基础上进行改进,提出最有前途分支启发式算法。实验中对任务的分配进行了验证,本文提出的任务分配和调度方法,能够有效地提高寻找最佳任务序列的效率,并同时提高任务完成的质量及数量。 图10 3种算法在不同约束条件下的比较(W/T=50) References) [1] SCHEE B A V. Crowdsourcing: why the power of the crowd is driving the future of business [J]. American Journal of Health-System Pharmacy, 2010, 67(4): 1565-1566. [2] MUSTHAG M, GANESAN D. Labor dynamics in a mobile micro-task market [C]// Proceedings of the 2013 SIGCHI Conference on Human Factors in Computing Systems. New York: ACM, 2013: 641-650. [3] DOAN A H, FRANKLIN M J, KOSSMANN D, et al. Crowdsourcing applications and platforms: a data management perspective [J]. Proceedings of the VLDB Endowment, 2011, 4(12): 1508-1509. [4] DEUTCH D, MILO T. Mob data sourcing [C]// Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2012: 581-584. [5] KAZAI G, KAMPS J, MILIC-FRAYLING N. Worker types and personality traits in crowdsourcing relevance labels [C]// Proceedings of the 20th ACM Conference on Information and Knowledge Management. New York: ACM, 2011: 1941-1944. [6] CHEN L, LEE D, MILO T. Data-driven crowdsourcing: management, mining, and applications [C]// Proceedings of the 2015 IEEE 31st International Conference on Data Engineering. Piscataway, NJ: IEEE, 2015: 1527-1529. [7] HOWE J. The rise of crowdsourcing [J]. Wired Magazine, 2006, 14(6): 1-5. [8] 冯剑红,李国良,冯建华.众包技术研究综述[J].计算机学报,2015,38(9):1713-1726.(FENG J H, LI G L, FENG J H. Summary of crowdsourcing technology research [J]. Chinese Journal of Computers, 2015, 38(9): 1713-1726.) [9] WONG C W, TAO Y, FU W C, et al. On efficient spatial matching [C]// Proceedings of the 33rd International Conference on Very Large Data Bases. [S.l.]: VLDB Endowment, 2007: 579-590. [10] LEONG H U, MAN L Y, MOURATIDIS K, et al. Capacity constrained assignment in spatial databases [C]// Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2008: 15-28. [11] TONG Y, SHE J, DING B, et al. Online mobile micro-task allocation in spatial crowdsourcing [C]// Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering. Piscataway, NJ: IEEE, 2016: 49-60. [12] TONG Y, SHE J, DING B, et al. Online minimum matching in real-time spatial data: experiments and analysis [J]. Proceedings of the VLDB Endowment, 2016, 9(12): 1053-1064. [13] HO C J, VAUGHAN J W. Online task assignment in crowdsourcing markets [C]// Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2013: 45-51. [14] HO C J, JABBARI S, VAUGHAN A J W. Adaptive task assignment for crowdsourced classification [C]// Proceedings of the 30th International Conference on Machine Learning. Atlanta: ICML, 2013: 534-542. [15] KARGER D R, OH S, SHAH D. Budget-optimal task allocation for reliable crowdsourcing systems [J]. Operations Research, 2011, 62(1): 1-24. [16] KAZEMI L, SHAHABI C. GeoCrowd: enabling query answering with spatial crowdsourcing [C]// Proceedings of the 20th International Conference on Advances in Geographic Information Systems. New York: ACM, 2012: 189-198. [17] TO H, FAN L, LUAN T, et al. Real-time task assignment in hyperlocal spatial crowdsourcing under budget constraints [C]// Proceedings of the 2016 IEEE International Conference on Pervasive Computing and Communications. Piscataway, NJ: IEEE, 2016: 1-8. [18] DANG H, NGUYEN T, TO H. Maximum complex task assignment: towards tasks correlation in spatial crowdsourcing [C]// Proceedings of the 2013 International Conference on Information Integration and Web-based Applications & Services. New York: ACM, 2013: 77-81. [19] GAREY M R, JOHNSON D S. Computers and Intractability: A Guide to the Theory of NP-Completeness [M]. New York: W. H. Freeman, 1990: 11-13. [20] VANSTEENWEGENAABA P. The orienteering problem: a survey [J]. European Journal of Operational Research, 2011, 209(1): 1-10. [21] LI Y, YIU M L, XU W. Oriented online route recommendation for spatial crowdsourcing task workers [C]// Proceedings of the 14th International Conference on Advances in Spatial and Temporal Databases. New York: ACM, 2015: 137-156. [22] DENG D, SHAHABI C, DEMIRYUREK U. Maximizing the number of worker’s self-selected tasks in spatial crowdsourcing [C]// Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2013: 324-333. [23] DENG D, SHAHABI C, ZHU L. Task matching and scheduling for multiple workers in spatial crowdsourcing [C]// Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2015: Article No. 21. [24] IPEIROTIS P G, PROVOST F, WANG J. Quality management on Amazon Mechanical Turk [C]// Proceedings of the 2010 ACM SIGKDD Workshop on Human Computation. New York: ACM, 2010: 64-67. [25] LIU X, LU M, OOI B C, et al. CDAS: a crowdsourcing data analytics system [J]. Proceedings of the VLDB Endowment, 2012, 5(10): 1040-1051. [26] CAO C C, SHE J, TONG Y, et al. Whom to ask?: jury selection for decision making tasks on micro-blog services [J]. Proceedings of the VLDB Endowment, 2012, 5(11): 1495-1506. [27] CAO C C, TONG Y, CHEN L, et al. WiseMarket: a new paradigm for managing wisdom of online social users [C]// Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2013: 455-463. [28] GAO J, LIU X, OOI B C, et al. An online cost sensitive decision-making method in crowdsourcing systems [C]// Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2013: 217-228. [29] KAZEMI L, SHAHABI C, CHEN L. GeoTruCrowd: trustworthy query answering with spatial crowdsourcing [C]// Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2013: 314-323. [30] TO H, SHAHABI C, KAZEMI L. A server-assigned spatial crowdsourcing framework [J]. ACM Transactions on Spatial Algorithms & Systems, 2015, 1(1): Article No. 2. [31] Yelp Inc. Yelp dataset [EB/OL]. [2017- 03- 20]. http://www.yelp.com/dataset challenge/. This work is partially supported by the National Natural Science Foundation of China (U1301252), the National Key Technology R&D Program (2013BAB06B04), the National Key R&D Program of China (2016YFC0400910), the National Science and Technology Major Project (2017ZX07104- 001), the Fundamental Research Funds for the Central Universities (2015B22214). MAOYingchi, born in 1976, Ph. D., associate professor. Her research interests include distributed computing, parallel processing, distributed data management. MUChao, born in 1993, M. S. candidate. His research interests include distributed computing. BAOWei, born in 1990, M. S. candidate. His research interests include distributed computing. LIXiaofang, born in 1972, Ph. D., associate professor. Her research interests include distributed computing.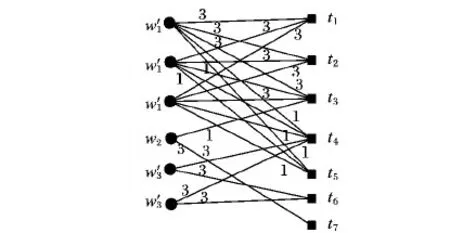
2.4 基于距离ε值分配算法
2.5 算法分析
3 任务调度
3.1 分支定界调度算法


3.2 最有前途分支启发式算法
4 实验验证与分析
4.1 实验环境


4.2 空间任务分配算法的实验分析


5 结语


