改进的异质大气光估计的图像去雾算法
余 朋,文小琴,汪兆栋,贺 乐
(华南理工大学 自动化科学与工程学院,广东 广州 510000)
0 引 言
近年来,有研究者提出利用多幅图像去雾,基于3D几何信息建模场景深度并去雾的思想[1-6]。然而,在单一图像去雾实验中,获得多幅图像或额外信息非常困难,因此限制了它们的应用。最近,基于单一图像而不使用额外信息的去雾算法取得了较大的进步[7,8]。比如自动颜色均衡化算法[9]、WP(White-point)算法[10],这些算法能获得良好的去雾效果,但由于没有考虑有雾图像的形成过程而导致图像部分细节信息的丢失,往往会产生不可预测的失真。何凯明等[11]提出了利用暗通道先验信息来实现图像去雾,但研究人员在后续实验中发现,该方法对那些类似于大气光的白色场景目标去雾效果不理想;Meng等[12]在何凯明等的基础上提出了一种利用图像内各目标间的边界信息来有效地正则化暗通道图,从而实现最终的去雾目的。虽然他们取得了较好的去雾效果,却易引起轻微的颜色失真,且计算相当复杂。为了克服上述算法的不足,针对单一图像去雾,本文作了以下工作:
(1)利用在有雾图像的亮度成分中进行“均值池化”的新思想进行“异质”大气光估计。
(2)提出了利用“非线性”颜色衰减先验模型来精确估计场景深度信息的算法。
(3)基于所估计的场景深度信息及“异质”大气光估计,提出了一种去雾系统。
1 背景工作
1.1 匀质大气散射模型
在过去几年里,根据McCartney等提出的“匀质”大气散射模型(homogeneous atmospheric scattering model,ASM),研究人员提出了各种各样的先进算法。该模型表示如下
I(x)=J(x)t(x)+A(1-t(x))
(1)
t(x)=e-βd(x)
(2)
式(1)中等号右边第一项是直接衰减项,用来描述场景辐射照度在介质中的衰减, 它随场景深度呈指数衰减;第二项被称为大气光幕,用来描述场景成像中加入的大气散射光, 它造成了场景的模糊和颜色的失真。I(x)是有雾图像,J(x)是无雾图像,x是场景中某个像素的二维坐标,A是“匀质”大气光,t(x)是介质传输率,β是介质传输系数,它由介质密度决定。d(x)描叙场景中某一位置深度。“匀质”大气散射模型因为考虑了光的吸收及散射而被广泛应用于图像去雾中,但是由于它假设整个场景中的大气光是匀质的而导致很多先进的算法去雾后的图像较暗。因此,采用“匀质”大气散射模型进行去雾的算法会导致图像变暗。
1.2 颜色衰减先验模型
Zhu等[13]首先提出了颜色衰减先验模型(color attenuation prior,CAP)。他们观察到,场景深度与HSV颜色空间中亮度和饱和度成分之间的差值有关。如图1所示,随着场景中雾的厚度增加,亮度和饱和度成分之差变大,反之亦然。

图1 图像中亮度和饱和度成分之间的差值
我们知道,雾的厚度和场景深度是正相关的。因此,他们对有雾图像数据集做了大量的统计分析,最后假设场景深度与亮度和饱和度成分之差呈线性关系。基于上述假设,他们提出了一个线性模型来估计有雾图像的场景深度,并通过基于合成有雾图像数据集的训练法获得该线性模型参数。通过该方法,他们在一些场景中取得了很好的去雾效果。但是,当我们使用该线性模型进行去雾实验时,发现该模型估计的场景深度出现了大量负值,尤其是比较靠近镜头并且几乎不受雾影响的场景对象,这是不合理的。
2 本文算法
在本节中,我们将通过估计异质大气光A(x),用非线性模型精确计算场景深度d(x)和介质传输率t(x),最终得到去雾图像J(x)。
2.1 改进的异质大气光估计
为了解决基于匀质大气光假设而得到的去雾图像较暗的问题,我们假设A(x)在整个场景中是可变的。即大气光是异质的或局部近似均匀的。由于大的场景对象对太阳光的遮挡,不同的场景对象具有不同的反射率或吸收率,场景中大气光呈现异质。改进的异质大气散射模型(ASM)公式如下
I(x)=J(x)t(x)+A(x)(1-t(x))
(3)
式(3)和式(1)的差别在于,式(3)中A(x)的值与位置x有关。为了准确估计异质大气光A(x),我们利用了“均值池化”的思想。首先,对亮度成分进行均值池化以获得较小的异质大气光图A″(x),并且这里用于池化的窗口大小是R×R。其次,利用双立方插值法将较小的异质大气光图A″(x)放大到原始有雾图像大小,以获得过渡的异质大气光图A′(x)。最后,将大气光图A′(x)归一化以调整最终获得的异质大气光图A(x)的下限。算法1说明了获得异质大气光A(x)的整个流程。实验结果如图2所示,它表明,采用本文改进的异质大气光估计A(x)的去雾图像要优于匀质大气光假设的去雾图像,并且图2(d)的异质大气光的估计结果也更合理。

图2 匀质和异质大气光去雾对比
算法1:改进的异质大气光估计
输入:亮度V(x),归一化参数ρ,窗口大小R
输出:A(x)
初始化:ρ=0.7,R=100;
A″(x)=meanPooling(V(x));
A′(x)=bicubicInterpoloation(A″(x));
Min=min(A′(x));
Max=max(A′(x))
2.2 非线性颜色衰减先验模型
为了克服由Zhu等提出的线性模型的缺点并精确估计场景深度,我们提出了一个非线性颜色衰减先验模型,它不仅可以解决出现许多负值的问题,而且还保持线性模型的一些优点。
(1)构造非线性模型
由于亮度和饱和度成分之间的差值可以近似地描述雾的厚度,我们可以建立一个非线性模型来估计场景深度,其表达式如下
(4)
式中:x表示有雾图像中坐标位置,d(x)是场景深度,V(x)和S(x)分别表示亮度和饱和度。θ0,θ1,θ2,α是未知非线性参数,α参数非常重要,表示原始有雾图像丰富的梯度信息,ε(x)是描述非线性模型随机误差的变量。
图3可以对式(4)进行形象地解释说明。图3中横轴表示亮度和饱和度成分之差,纵轴表示场景深度。在我们的非线性模型中,场景深度是不可能为负值的,而线性模型在区间a中却出现了很多负值。非线性模型在区间b还可以很好地近似线性模型,并保持线性模型的一些优势。除此之外,它也表明非线性模型可以很好地近似人类视觉系统的成像机制。我们使用均值为0,方差为σ2的高斯函数ε(x),ε(x)~N(0,σ2)。由高斯分布的性质我们得出

(5)
已知d(x)的分布,我们可以通过简单有效的监督学习法获得模型参数θ0,θ1,θ2,α。下面对该监督学习法进行详细地阐述。

图3 线性及非线性模型估计场景深度值对比
(2)合成有雾图像训练数据集
为了获得精确的模型参数θ0,θ1,θ2,α。我们需要一个包括有雾图像及其相应的场景深度标注信息的数据集。然而,现实中没有能够满足我们要求的且已收集好的训练数据集。因此我们利用“无雾”的图像数据集合成了一个“有雾”的图像数据集[14]。在得到合成的有雾图像数据集过程中,我们首先从网上收集449张无雾图像,然后分别在区间[0,1]和[0.80,0.95]上为每个无雾图像随机生成深度图d(x)和大气光图A(x)。由于我们逐个像素地对模型进行训练,所以我们不需要遵循以往的假设,即场景深度局部近似相同以生成场景深度图d(x)或大气光图A(x)。
(3)训练非线性CAP模型
我们已经在上文中描述了单个像素服从的场景深度分布规律,但是,我们需要考虑所有图像中的像素。因此,我们构造了联合条件分布函数
L=p(d(x1),…,d(xn)|x1,…xn,θ0,θ1,θ2,α,σ2)
(6)
式中:n表示像素的总量,d(xn)是第n个场景点的深度。L表示似然函数。在训练期间,我们假设各像素的随机误差是彼此独立的。然后我们可以推导出以下公式
(7)
将式(5)代入式(7),得到似然函数的具体形式
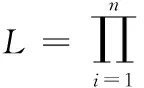
(8)
式中:dgi描述了场景深度标注信息(即随机生成的场景深度标注信息),于是我们的目标转换为寻找θ0,θ1,θ2,α的最优解来最大化似然函数L。为了简单起见,我们将式(8)用一个简单的形式表示

(9)
同时,我们避开直接求似然函数L的最大值,而是求其对数lnL的最大值。因此,该问题转化为求式(10)的最大值
(10)
为了求解上述问题,我们首先计算lnL对的导数,并且让它等于零
(11)
根据式(11)可以求得σ2的最大似然估计值
(12)
对于非线性参数θ0,θ1,θ2,α, 我们通过自适应SGD[15]算法估计它们的值。分别对θ0,θ1,θ2,α求导,得到下列各式
Ti=(dgi-di)*(1-di)*di
(13)
(14)
(15)
(16)
(17)
用于更新非线性参数的方程可以简洁地表示为

(18)
算法2:非线性CAP模型的参数估计
输入:亮度向量V(x),饱和度向量S(x)和场景深度向量d(x)
输出:非线性参数θ0,θ1,θ2,α,σ
初始化:α=5,θ0=0,θ1=1,θ2=-1,Su=0,αSum=0,wsum=0,vSum=0,sSum=0,learnRate=0.002;
对于i∈[1,n]
temp=dgi-di;
temp1=θ0+θ1*V(xi)+θ2*S(xi);
Su=Su+temp2;

vSum=vSum+temp*(1-di)*di*α*V(xi);
sSum=sSum+temp*(1-di)*di*α*S(xi);
αSum=αSum+temp*(1-di)*di*temp1;
θ0=θ0+learnRate*wSum/n;
θ1=θ1+learnRate*vSum/n;
θ2=θ2+learnRate*sSum/n;
α=α+learnRate*αSum/n;
算法2呈现了学习非线性参数θ0,θ1,θ2,α和变量σ2的详细过程。我们用449个样本训练该非线性模型,所有样本总共包含2.1552亿个场景点。模型终止训练的准则是两次连续迭代的均方误差值(MSE)的差小于一个人为设定的迭代阈值。最后的模型训练结果是α=4.99,θ0=-0.29,θ1=0.83,θ2=-0.16。有了这些参数估计值及前面建立的场景深度有d(x),亮度V(x)和饱和度S(x)之间的非线性关系,就可以精确计算出场景深度,从而实现单一图像去雾。
2.3 估计场景介质传输率
已知估计的场景深度,我们可以很容易地通过式(2)计算场景介质传输率。然而,雾的厚度不仅由场景深度决定,而且还取决于介质密度。事实上,由于各种人为或自然因素,介质密度往往因场景而异。因此,不同场景的β值也不同。在我们的实验中,发现它分布于区间[1.1,2.0]上。然而,当值较大时,将导致t(x)的某些值接近于零,这是不合理的,尽管其对于某些场景点去雾效果良好,但是容易导致对远处场景点的不自然去雾效果,因此,我们限制t(x)值大于t0。
2.4 图像去雾
利用先前估计的场景介质传输t(x)和改进的异质大气光A(x),我们可以求解式(3)得到去雾后的图像J(x)的表达式。结果如下
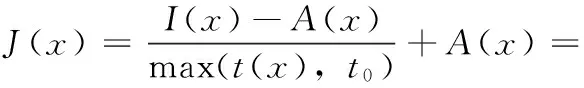
(19)
至此,我们实现了最终的图像去雾目的。
3 实验结果及分析
在合成的和自然的有雾图像上,我们进行了广泛的定性和定量比较实验。以此验证我们算法的有效性。
3.1 定性比较
我们将所提出的算法与一些先进的算法进行比较,包括DCP[11],BCCR[12],CAP[13],其定性比较结果如图4所示。从图可知,对于第一行有雾航拍图像,DCP,BCCR和CAP算法去雾后的图像变得非常暗,而利用本文提出的异质大气光A(x)的假设及相应算法得到的结果则非常明亮。此外,你会发现BCCR算法擅长处理远处的雾霾场景,而对于较近的场景则去雾不彻底。CAP算法不能在整个场景中实现完全去雾的目的,我们的结果则不会出现该问题。将上述算法应用于第二行有雾的南瓜图像得到了相同的结果。对于最后两张有雾图像,采用BCCR算法出现了颜色失真,而采用DCP和CAP算法仍然会出现亮度较暗和去雾不彻底现象。总之,我们的结果可以克服所有这些算法的缺陷,并获得预期的去雾效果。
3.2 定量比较
为了验证本文非线性模型精确估计场景深度的有效性,我们使用十对立体无雾图像和他们相应的场景深度图像来合成有雾图像,然后采用我们的非线性模型和其它算法估计该合成的有雾图像的场景深度图。最后,我们计算真实场景深度图和估计的深度图之间的平均MSE。虽然这些算法中有的只能估计场景介质传输图t(x),但由于在合成有雾图像时,β值已知,故它们可以通过式(2)间接地估计场景深度图。因此,对于所有算法来说,表1的对比结果是合理的。
在表1中,最好的结果用粗体表示。如表1所示,我们对于aloe,baby,cones,dolls等图片的场景深度的估计效果是最好的,但是也有些图片例外,诸如art,laundry,teddy图片。在表1的最后一行中,我们计算了所有图片的平均MSE。显然,我们的结果是最好的,因为我们可以克服CAP算法的缺陷,即该算法在估计场景深度时出现了许多明显不合理的负值(如图3所示)。DCP算法结果相对来说最差,因为其对场景深度的不良估计导致去雾过度。

图4 定性对比

方法DCPBCCRCAP本文方法aloe11.40951.40800.02130.0101art10.68880.93050.03110.0316baby11.21591.18020.03030.0239cones10.49250.92980.01210.0088dolls10.60030.92130.01360.0099Laundry10.53210.96240.01300.0173plastic9.70870.59330.02090.0135reindeer10.41820.97990.03560.0306teddy11.02141.04950.01520.0167TotalMSE10.72781.00540.02170.0176
4 结束语
本文提出了一种基于改进的异质大气光估计和非线性颜色衰减先验模型的有效的去雾算法。该算法不仅可以解决现有算法DCP、BCCR和CAP导致去雾后的图像变暗的问题,而且还可以克服由线性颜色衰减先验模型产生的许多场景深度估计值为负数的缺陷,并保留有雾图像的丰富的梯度信息。实验结果表明,我们所提出的算法可以获得高质量的去雾图像,其结果甚至比现有的方法更好。
[1]SUN Xiaoming,SUN Junxi,ZHAO Lirong,et al.Improved algorithm for single image haze removing using dark channel prior[J].Journal of Image and Graphics,2014,19(3):381-385(in Chinese).[孙小明,孙俊喜,赵立荣,等.暗原色先验单幅图像去雾改进算法[J].中国图象图形学报,2014,19(3):381-385.]
[2]WU Di,ZHU Qingsong.The latest research progress of image dehazing[J].Acta Automatica Sinica,2015,41(2):221-239(in Chinese).[吴迪,朱青松.图像去雾的最新研究进展[J].自动化学报,2015,41(2):221-239.]
[3]Wang Yating,Feng Ziliang.Single image fast dehazing method based on dark channel prior[J].Journal of Computer Applications,2016,36(12):3406-3410.
[4]YANG Ting.Research on fog removal methods of multiple images[D].Dalian:Dalian Maritime University,2013:38-53(in Chinese).[杨婷.多幅图像去雾算法研究[D].大连:大连海事大学,2013:38-53.]
[5]LIU Tongjun.Research of image dehazing based on multiple polarization images[J].Journal of Hunan University of Technology,2016,30(2):37-42(in Chinese).[刘同军.基于多幅偏振图像的去雾研究[J].湖南工业大学学报,2016,30(2):37-42.]
[6]Davis MA,Kazmi SMS,Dunn AK.Imaging depth and multiple scattering in laser speckle contrast imaging[J].Journal of Biomedical Optics,2014,19(8):086001.
[7]Xu Y,Guo X,Wang H,et al.Single image haze removal using light and dark channel prior[C]//IEEE International Conference on Communications in China.IEEE,2016:1-6.
[8]Ullah E,Nawaz R,Iqbal J.Single image haze removal using improved dark channel prior[C]//Proceedings of International Conference on Modelling,Identification & Control.IEEE,2013:245-248.
[9]Cheon M,Lee W,Yoon C,et al.Vision-based vehicle detection system with consideration of the detecting location[J].IEEE Transactions on Intelligent Transportation Systems,2012,13(3):1243-1252.
[10]Deb SK,Nathr RK.Vehicle detection based on videofor traffic surveillance on road[J].International Journal of Computer Science & Emerging Technologies,2012,3(4):121-137.
[11]Sun J,He K,Tang X.Single image haze removal using dark channel priors[P].U.S:8340461,2012-12-25.
[12]Meng G,Wang Y,Duan J,et al.Efficient image dehazing with boundary constraint and contextual regularization[C]//IEEE International Conference on Computer Vision.IEEE,2013:617-624.
[13]Zhu Q,Mai J,Shao L.A fast single image haze removal algorithm using color attenuation prior[J].IEEE Transactions on Image Processing,2015,24(11):3522-3533.
[14]Tang K,Yang J,Wang J.Investigating haze-relevant features in a learning framework for image dehazing[C]//IEEE Conference on Computer Vision and Pattern Recognition.IEEE,2014:2995-3002.
[15]He J,Zhang Y,Zhou Y,et al.Adaptive stochastic gradient descent on the Grassmannian for robust low-rank subspace recovery[J].IET Signal Processing,2016,10(8):1000-1008.

