海南木麻黄不同形数对比分析
朱光玉,胡 松,肖前辉 ,银勇平
(1.中南林业科技大学 林学院,湖南 长沙 410004;2.国家林业局 中南林业调查规划设计院,湖南 长沙 410014)
形数是树干材积与等底、同高的比较圆柱体体积之比。不仅是反映树干饱满程度的重要干形指标,也是计算立木材积及林分蓄积量的重要因子[1-3]。早在19世纪初,德国林学家在计算树干材积和确定其变化规律的同时,就创立了形数的理论。此后有诸多研究者,如斯马林(1873)、Girard J W(1933)、Maoss A(1939)、苏联的丘林教授(1950)及我国的林昌庚教授(1961)等都提出了不同的干形指标和模型,从多方面对干形做了研究[4]。其中,斯马林首创提出了正形数,以克服胸高形数随树高生长而变化的缺点[5]。林昌庚教授吸取胸高形数量测方便和正形数不受树高影响的优点,根据实践经验提出了“实验形数”[6-7]。刘守亚教授于1976年参照实验形数的设计思路设计了D形数,后又于1977年设计了DH形数[8]。1997年吴纪昌等提出的新绝对形数是在该研究领域漫长沉寂之后的又一次成功的探索[9]。
尽管很多林学家们试图完善这一理论,但对形数的研究却大多偏重理论推导,在实际中的应用却相对较少[10-13]。杜纪山(1989)用陕南、陕北林区16个油松Pinus tabulaeformis Carr标准地材料,计算各相对高处的林分正形数系列样本平均值、标准差和变异系数,初步得出正形数系列在林分内和林分间的变化规律[14-17]。JV Silva等(1994)用地上15.2 cm和1.52 m处的树干直径测量值推导柱体形数估计值,将它用于火炬松Pinus taeda Linn.、湿地松Pinus elliottii Engelmann和加勒比松Pinus caribaea Morelet的计算,表现良好,但它只适用于没有明显干基膨大的树种[18-19]。杨华、孟宪宇等(2005)以正形数为基础,提出V=f0.1h× g0.1h×h的单株立木材积估测式,经6个树种944株样木试验,并与二元立木材积表法进行了比较,取得了良好的效果[20]。陶涛、唐巍(2009)利用四川杉木解析木材料,对胸高形数、实验形数、D形数、DH形数及其变幅率、变动系数的研究表明4种形数的变幅率和变动系数均随胸径、树高的变化而变化,却不因形数种类不同而有明显差异[21]。
由于林木干形受内外多重因素影响,不同树高处的干形不同,形数存在显著差异。而形数作为重要的测树因子,既决定着树干材积的数量和质量,还是某些测树用表编制的主要依据,其变化直接影响到林木材积及材种出材量。而且不同的形数对树干形状的反映有所不同,采用形数法预测单株立木材积具有很大的差异性,所以在林业生产中对形数的选择尤为重要。本文将以海南木麻黄为研究对象,研究胸高形数、实验形数与不同相对树高处正形数的变化规律,并进行对比分析,寻找其中最稳定的形数,为木麻黄材积预测及经营数表编制等工作提供理论依据。

表 1 木麻黄树高与胸径特征统计Table 1 Characteristics of tree height and diameter at breast height for Casuarina equisetifolia
1 研究区概况
研究区位于中国最南端的海南省,东经108°21′~ 111°03′, 北 纬 19°20′~ 20°10′, 地 处热带北缘,属热带季风气候。全省陆地总面积3.39×104km2,其中有林地面积2 066.67 hm2,森林覆盖率达60.2%。海南全年暖热,干湿季节明显,是我国最具热带海洋气候特色的地方。土壤以红壤为主,养分充足,生物生长繁殖迅速。年平均气温在23~26 ℃之间,光温充足,光合潜力高,是中国南方理想的繁育种基地。海南岛全年无冬,全岛降雨充沛,年降水量1 000~2 600 mm,降雨季节分配不均匀,每年的5—10月份是多雨季。海南岛四周低平,中间高耸,山地、丘陵、台地、平原构成环形层状地貌,梯级结构明显。
木麻黄Casuarina equisetifolia是我国华南沿海地区的主要防护林树种之一,自20世纪50年代,在华南沿海地区被广泛种植,具有生长迅速、萌芽力强、耐盐碱及抗风沙等特点。
2 研究方法
2.1 数据采集与整理
在研究区内,采用抽样调查的方法分别从不同立地条件、林分年龄和林分密度的木麻黄林分内,选取216株木麻黄活立木作为解析木,伐倒后测定每株样木的树高及树干(根颈0 m、胸高1.3 m、1/10 h、2/10 h、……、9/10 h)处的带皮直径。216株木麻黄胸径与树高相关统计量见表1。
2.2 形数计算
将216株木麻黄伐倒木分别以1/10树高进行区分段划分,利用平均断面积区分求积法计算各样木的材积作为材积真实值。根据形数的定义,以材积真实值与不同树高处的断面积作比较圆柱体断面积的比较圆柱体体积之比,分别计算胸高形数、实验形数与相对高处的正形数,11种木麻黄形数计算结果见表2。
(1)平均断面积区分求积式
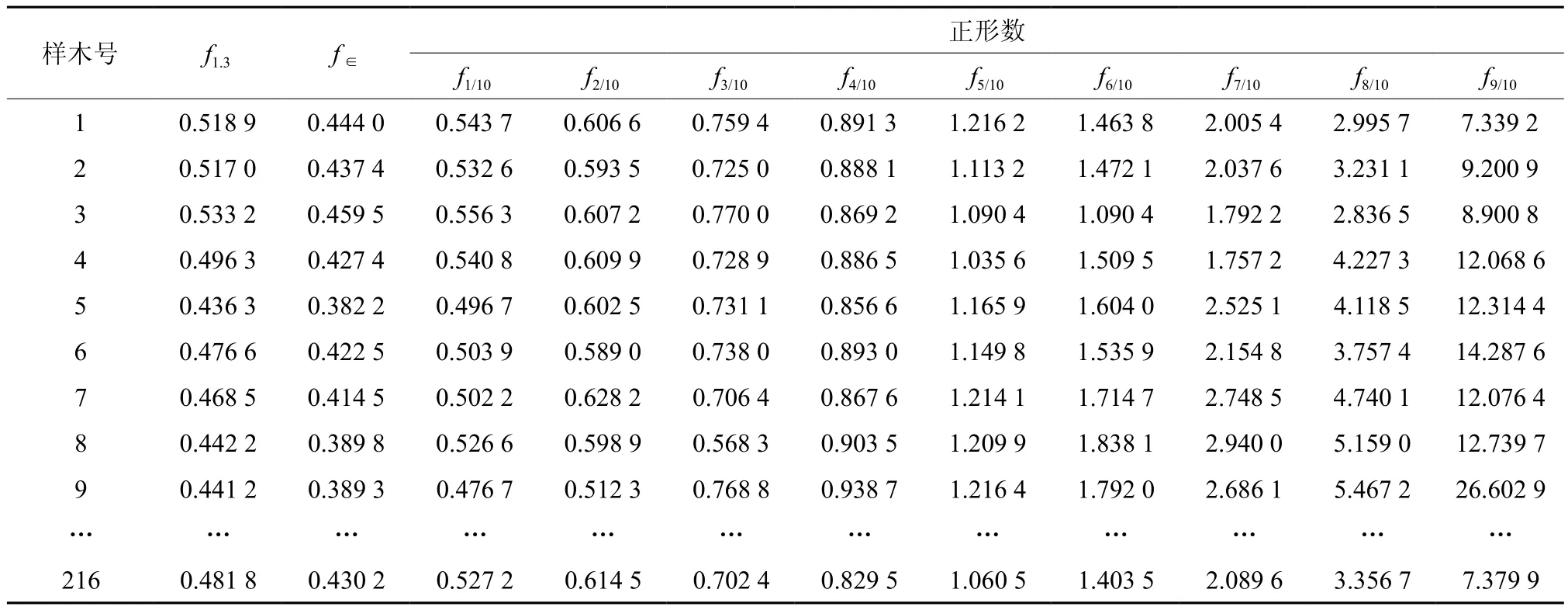
表 2 木麻黄胸高形数、实验形数与正形数Table 2 Breast-height form factor, experimental form factor & normal form factor of Casuarina equisetifolia

式中:V真为真实材积,用实测材积替代;V比为比较圆柱体体积,g0为树干底断面积;gn为梢头底断面积;gi为各区分段之间的底断面积;l、l′分别为区分段长度与梢头长度。
(2)根据胸高形数定义

式中:f1.3为胸高形数;d1.3为胸高直径;h为树高。
(3)根据实验形数定义
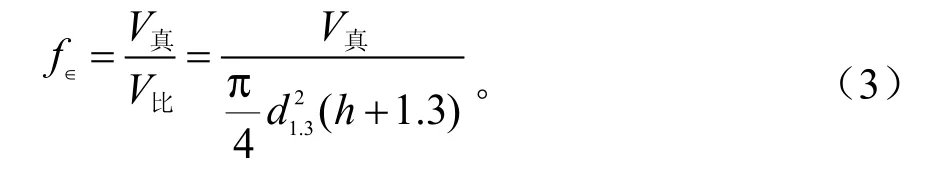
式中:f∈为实验形数;d1.3为胸高直径;h为树高。
(4)根据正形数定义

式中:fn为相对高nh处的正形数;dn为相对高nh处的直径;h为树高;n=1/10、2/10、3/10、… 、8/10、9/10。
2.3 分析方法
(1)变异系数法
变异系数(CV),也称差异系数、离散系数,常采用标准差与平均数的比值来比较两个或多个样本数据变异程度的高低,是衡量样本数据中各观测值变异程度的重要统计指标。变异系数具有直观简洁的优点,与方差相比,可以消除平均数不同对两个或多个样本变异程度比较的影响。计算公式为:

(2)相关分析法
相关分析是描述两个变量之间线性相关程度的分析方法,常以两个变量与各自平均值的离差为基础,通过离差相乘,计算相关系数r来反映两个变量之间相关关系的密切程度。相关系数r取值在-1到1之间,|r|越大,变量间的相关程度越高。

式中:r为相关系数;yi为材积实测值;xi为比较圆柱体体积;为材积实测值的平均值;为比较圆柱体体积的平均值;n为样本数。
(3)回归分析法
回归分析是指运用统计学的理论与方法建立变量之间的数学方程式,检验和比较一个或一组变量对所关注变量的影响程度,进而预测所关注变量的变化趋势,从而确定两种或两种以上变量间相互关系的一种统计分析方法。一般线性回归模型:

依据形数的定义:
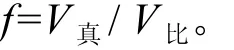
可得:

模拟实测材积与比较圆柱体材积之间的相关关系,参数b即为形数f。模型精度越高表示形数f越稳定。因此,可采用不含常数的线性回归模型:
模型检验采用确定系数R2和平均绝对误差(MAE)来衡量模型模拟的精度高低。其中确定系数也称拟合优度,R2越接近于1,表明模型精度越高。平均绝对误差(MAE)值越小,模型对材积实测值与比较圆柱体体积的相关关系预估越准确,模型精度也就越高。
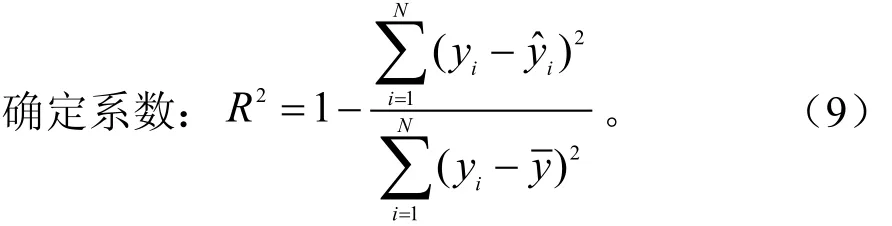
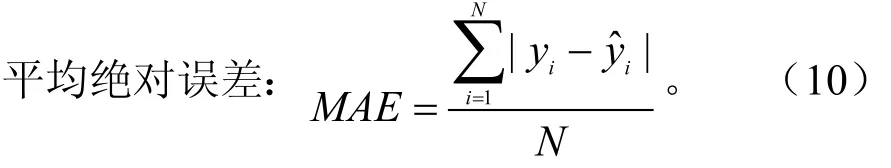
式中:yi为材积实测值;为材积预测值;为材积实测值的平均值;N为样本数。
3 结果与分析
3.1 不同形数依树高变化规律
为研究木麻黄胸高形数、实验形数与相对高处正形数随树高的变化特点及形数间的差异性,本研究将216株木麻黄解析木以2 m为间距,划分为10个树高级,各树高级所包含的样本最少为11株,最大为47株,分别计算各树高级所对应形数的平均值(表3)。为了更直观地反映不同形数随树高级的变化规律,根据表3绘制折线图(见图1)。
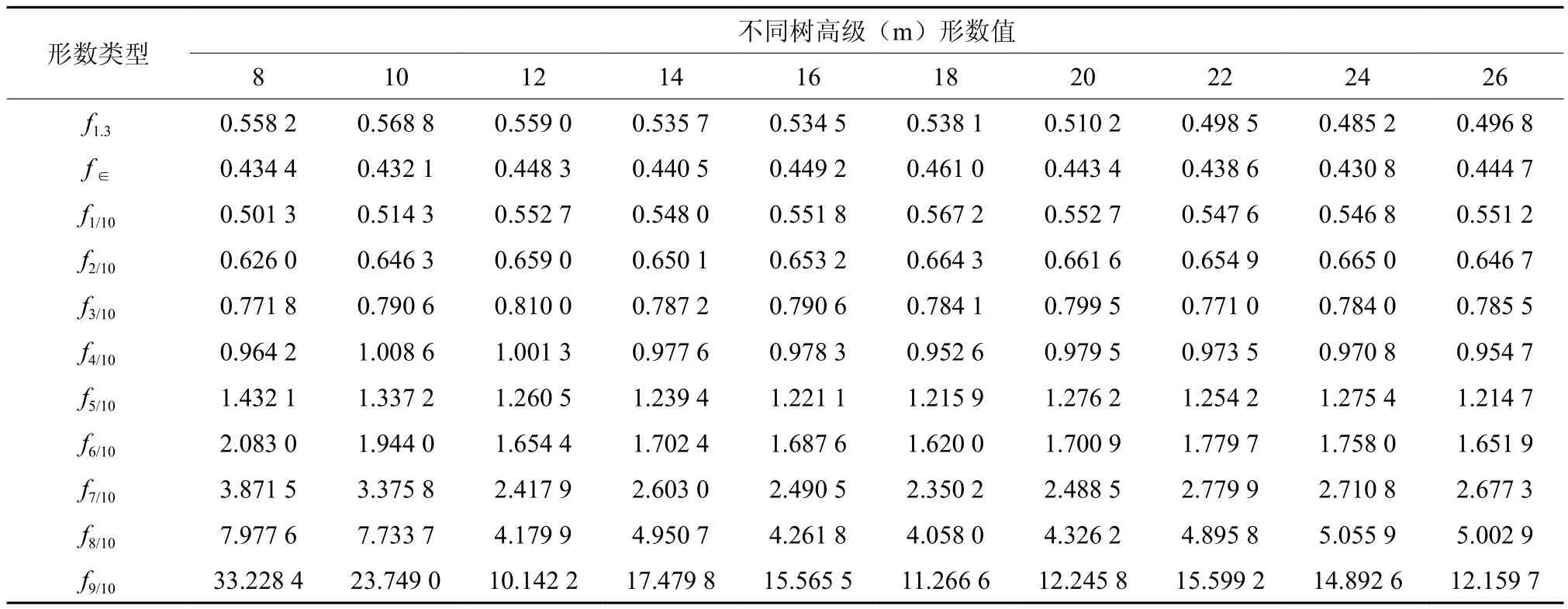
表 3 木麻黄不同形数随树高级的变化Table 3 Different form factors of Casuarina equisetifolia vary under different height classes
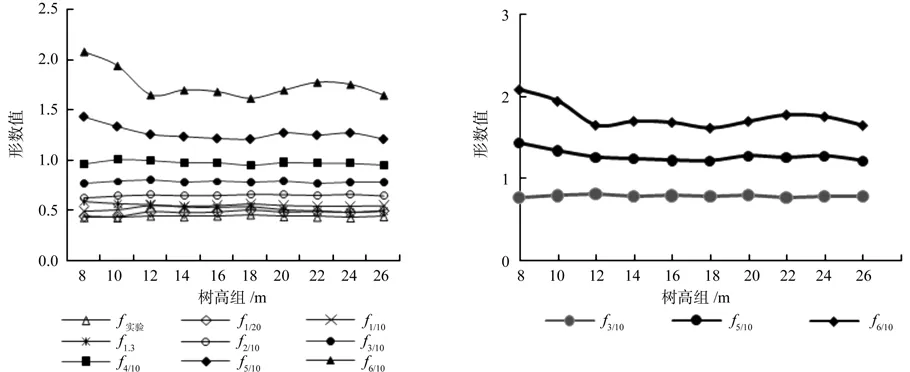
图1 木麻黄不同形数依树高级的变化Fig.1 Casuarina equisetifolia different form factors vary with height classes
由图1可以看出,对于不同的形数,随着树高级的增加,形数均值的变化呈现一定的规律性:(1)前8种形数的变异情况较小,后3种形数的变动情况较大;(2)随着树高级的增加,前8种形数均值基本上逐渐变小,而后3种形数呈现不规则变化状态。为了分析各形数的变化程度,将采用变异系数法、相关分析法和回归分析法进行进一步研究。
3.2 形数稳定性分析
由上述木麻黄形数依树高级变化规律可知:小于7/10树高的形数随着全树高的变化其变化不明显,树高7/10至9/10处的木麻黄形数变化较大。为了进一步分析木麻黄形数变化规律,探索胸高形数、实验形数与相对高nh处正形数的变异情况,将采用变异系数、相关分析和回归分析3种方法分别进行处理。
3.2.1 变异系数分析
变异系数是反映一组数据或一个变量变动大小的指标,通过变异系数的大小可以对比不同形数间的变异程度,比较不同形数的稳定性。变异系数越小,变动范围越小,反之越大。根据平均数、标准偏差及变异系数的定义,对胸高形数、实验形数与相对高nh处正形数进行统计分析,结果见表4。

表 4 不同形数样本的平均数、标准偏差及变异系数Table 4 The mean, standard deviation and coefficient of different form factors
由表4可知:木麻黄胸高形数、实验形数与相对高nh处正形数变动幅度在0.044 4~0.637 8之间;相对高nh从3/10到9/10,随树高增大形数变动程度越大,稳定性越差;在3/10相对高处的正形数变异系数最小,其均值为0.713,即该相对高处正形数稳定性最好,要优于胸高形数、实验形数等。
3.2.2 相关分析
利用相关系数,分析木麻黄材积实测值与不同树高处的比较材积之间的相关系数,进行相关程度比较。相关系数越接近于1,其相关性越大,表示该比较圆柱体所对应的形数越稳定。不同树高处比较圆柱体体积与材积实测值的相关系数如表5所示。
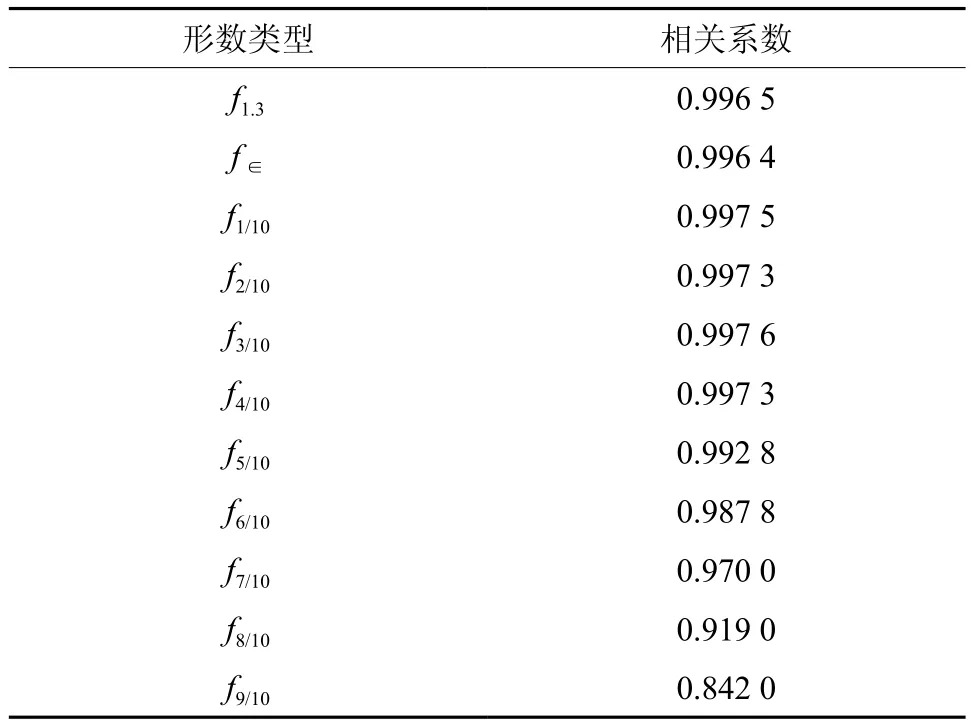
表 5 不同比较圆柱体与其实测值的相关系数Table 5 The correlation coefficient between comparative cylinder with measured values
由表5可知:不同形数所对应的比较圆柱体体积与其材积实测值的相关系数具有很大的差异性,相关系数变动范围为:0.842 0~0.997 6之间,在1/10、2/10、3/10、4/10相对高处形数相关系数最接近于1,且3/10相对高处的相关系数最大,即该树高处的比较材积与材积实测值的相关性最高,表明其所对应的形数最稳定。
3.2.3 回归分析
以材积实测值与不同形数所对应的比较圆柱体体积分别作为因变量、自变量构建线性回归模型,利用SPSS软件求解模型参数a。统计各模型模拟的预测值与残差,并分别计算确定系数(R2)与平均绝对误差(MAE)以分析回归模型精度,结果见表6。
由表6可知,胸高形数、实验形数与相对高nh处正形数对应的回归模型存在显著差异,一般随树高增大,参数值增大,即形数值随树高增大而增大。回归模型的确定系数在1/10h、2/10h、3/10h、4/10h处最接近于1,其中3/10h处确定系数最大,相应回归模型精度最高。而且模型在3/10h处的平均绝对误差最小,说明该处回归模型预测值与真实值最接近。
根据3/10处的形数回归模型,建立预测值与残差的关系图(图2)。由图2可知:残差值比较均匀的分布在横轴两侧,且两侧残差距横轴距离大致相等,仅有个别点远离横轴,表明该回归模型精度较高。

表 6 回归模型精度分析Table 6 Accuracy analysis ofregression models
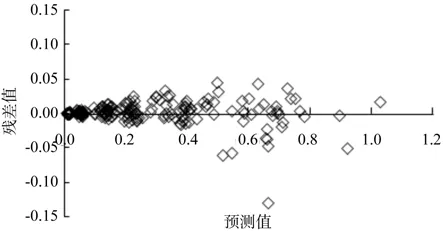
图2 3/10树高处残差分布Fig.2 Residuals distribution of 3/10 tree height
3.2.4 比较与分析
通过变异系数分析、相关分析和回归分析,3种方法对形数变异程度的分析结果均表明:木麻黄在3/10处形数变异程度最小,稳定性最高。其中,变异系数法利用变异系数直接反映不同形数组内差异程度的高低,消除了形数平均值不同对组间变异程度比较的影响,但变异系数不能反映形数组间的相关程度。相关分析则以实测材积、比较圆柱体体积两组变量的相关系数直接描述两者组间相关性的大小,但与变异系数相反的是不能反映变量组内的离散关系。回归分析则通过构建不含常数的线性回归方程,从线性相关关系出发,以模型精度高低评价实测材积与比较圆柱体体积的相关性,间接反映了形数的稳定性。
3.3 相对高处直径与胸径的相关关系
利用3/10h处正形数进行活立木材积估算时,需要测量树高与3/10h处直径。但是采用常规的测量手段,相对高处直径难以有效测量。虽然随着测树工具的改进和发展,利用近景影像处理技术或光学测定仪器,已经可以准确测量树干上任意部位的直径[22-23],但直径提取技术还不成熟,提取速度慢、耗时长且精度不高,所以3/10 h处正形数的实际应用仍存在困难。
杜纪山[14]在研究陕西油松的正形数系列变化规律时,发现相对高处的直径与胸径呈紧密的线性关系,通过测量胸径可以有效预估相对高处的直径,从而利用正形数进行单株立木材积计算。本文根据木麻黄相对高处直径与胸径的相关关系,建立木麻黄各相对高处直径与胸径的散点分布图(图3)。从图3中可以看出各相对高处直径与胸径的散点呈近直线分布,两者的线性关系显著。
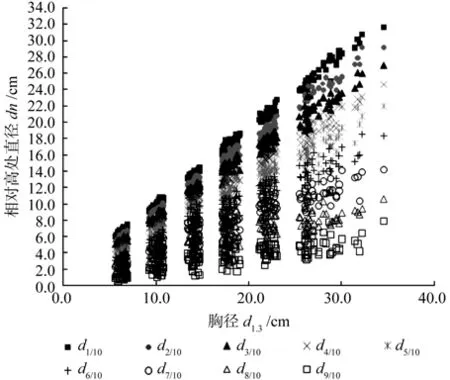
图3 相对高处直径与胸径的散点分布Fig.3 The scatter distribution of diameter at relative tree height and diameter at breast height
根据相对高处的直径与胸径的线性相关关系,以胸径为自变量、3/10h处直径为因变量,建立3/10h处直径与胸径的线性回归模型(图4)。利用SPSS求解模型参数,并进行精度分析。结果发现:d3/10与d1.3的线性回归方程为d3/10=0.767 9d1.3+0.696 4,模型确定系数(R2)为0.991 1,平均绝对误差(MAE)为0.389 5,模型模拟效果较好。
通过d3/10与d1.3的线性回归方程,可以推算3/10h处直径的预测值。并根据正形数的定义,计算所对应的修正形数分别以3/10相对高处形数、修正形数、胸高形数与实验形数的平均值作为平均形数(利用平均形数法求算木麻黄单株材积,并以确定系数(R2)与平均绝对误差(MAE)作为模型评价指标,对的预估效果进行检验分析,结果见表7。
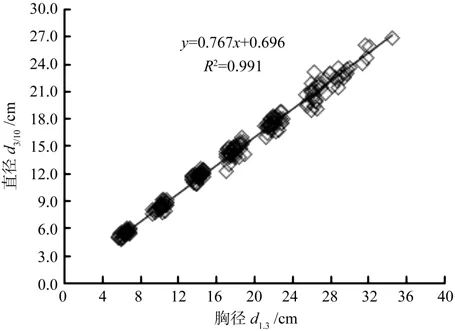
图4 3/10h处直径与胸径的相关关系Fig.4 The relationship of diameter at 3/10 tree height and diameter at breast height
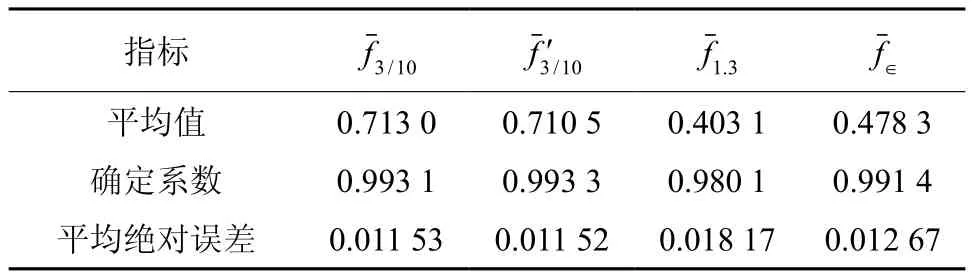
表 7 形数预估效果的检验分析Table 7 The examination of form factor estimate effection
4 结论与讨论
形数作为立木材积三要素之一,对于单木材积的计算具有十分重要的作用。本研究以海南省216株木麻黄解析木为研究对象,采用变异系数分析、相关分析和回归分析3种方法,对比分析了胸高形数、实验形数与相对高nh处正形数的变异程度。由11种形数变异系数的变化情况可知,形数f3/10的变动系数最小,说明对于不同年龄、胸径和树高的木麻黄,3/10h处的正形数稳定性最高。而且相关分析和回归分析结果均显示:3/10h处的相关系数r和模型模拟的确定系数R2也最大,分别为0.997 6和0.995,表明该相对高处的形数f3/10最稳定。3种分析方法从组内变异程度与组间相关性大小的角度,论证了木麻黄正形数f3/10的稳定性。由于3/10h处的正形数直径随树高变化而难以测量,f3/10的实用性将受到影响。本研究根据相对高处直径与胸径的相关关系,建立了直径d3/10与胸径d1.3的回归预测模型:d3/10=0.767 9d1.3+0.696 4,R2=0.991 1。并利用平均形数法分别对的预估效果进行检验分析:模型确定系数(R2)0.993 1,平均绝对误差(MAE)0.011 53;模型确定系数(R2)0.993 3,平均绝对误差(MAE)0.011 52;模型确定系数(R2)0.980 1,平均绝对误差(MAE)0.018 17;模型确定系数(R2)0.991 4,平均绝对误差(MAE)0.012 67,结果证明了3/10h处的正形数要优于实验形数与胸高形数,且修正后的最优。通过建立3/10h处直径的回归预测模型,为木麻黄3/10h处形数的有效应用提供了途径和依据。
本研究利用数理统计方法分析了胸高形数、实验形数与相对高nh处正形数的变异程度,通过建立3/10h处直径的回归预测模型,有效解决了木麻黄3/10h处形数的应用问题,对正形数的生产应用提供了思路参考。但由于研究所用数据有限,对修正后的(0.710 5)缺乏有效的适用性检验,可以考虑在增加样本数量的基础上,研究更大范围的木麻黄形数变化。研究结果对于利用形数法求算木麻黄单株材积或林分蓄积具有一定的指导意义。
[1]孟宪宇.测树学[M].北京:中国林业出版社,2006.
[2]刘守亚.关于干形控制方法的几点意见[J]. 林业勘查设计,1976(1):30-33.
[3]张剑英.树干形数研究进展[J].山西林业科技,2003(2):1-3.
[4]曲 佳,张雄清.国内外树干干形的研究进展[J].林业实用技术,2015(7):3-7.
[5]孟宪法,李悦黎,白林波.树干形状应用研究进展[J].陕西林业科技,2000(3):60-65.
[6]林昌庚.关于实验形数(一)[J].林业勘查设计,1964(2):11-19.
[7]林昌庚.关于实验形数(二)[J].林业勘查设计,1974(3):17-28.
[8]刘守亚.关于干形控制方法的几点意见[J].林业勘查设计,1976(1):30-33.
[9]吴纪昌,李铁民.胸高圆锥系数和新绝对形数的研究[J].山西林业科技,1997(4):1-5.
[10]钟德军,李淑阁,杨景辉,等.落叶松干形研究[J].河北林果研究,2004,19(2):126-129.
[11]吴玉德.天然赤松立木干形研究[J].林业实用技术,2008(9):9-11.
[12]满文慧,崔雅君,李国林.天然长白松干形的研究[J].吉林林业科技,2006,35(6):21-25.
[13]范广信,张景兰,郄利军,等.实验形数变化规律的研究[J].河北林果研究,2006,21(1):33-36.
[14]杜纪山.正形数系列变化规律的初步研究[J].陕西林业科技,1989(2):007.
[15]杜纪山.带、去皮正形数系列之间的变化规律及应用[J].浙江林业科技,1990,10(2):20-23.
[16]杜纪山.正形数fh/4在角规法调查油松林分蓄积量中的应用[J].林业实用技术,1989(5): 25-27.
[17]杜纪山,常 昆.油松正形数f(0.15h)的性质及其应用[J].林业实用技术,1993(2):007.
[18]Da Silva A, Antonio J, Borders B E. A Tree Volume Equation Based on Two Lower Stem Diameters for Loblolly Pine in the Southeastern United States[J].Southern Journal of Applied Forestry,1993,17(4):160-162.
[19]DA Silva JAA, Borders BE, Brister GH. Estimating tree volume using a new form factor[J].The Commonwealth Forestry Review,1994:14-17.
[20]杨 华,孟宪宇,程 俊,等.利用正形数估测立木材积方法的研究[J].林业资源管理,2005(1): 39-41.
[21]陶 涛,唐 巍.四川杉木单株木4种形数及其变异研究[J].四川林勘设计,2009(1):15-18.
[22]杨 华.近景摄影测量技术在立木材积测定中的应用研究[D].北京:北京林业大学,2003.
[23]刘伟乐,林 辉,孙 华,等.基于地面三维激光扫描技术的林木胸径提取算法分析[J].中南林业科技大学学报,2014, 34(11):111-115.

