神光III主机上球腔辐射场实验的三维数值模拟与分析∗

李树 陈耀桦 姬志成 章明宇 任国利 霍文义 闫威华韩小英 李志超刘杰3)4) 蓝可3)4)

1)(北京应用物理与计算数学研究所,北京 100094)

2)(中国工程物理研究院,激光聚变中心,绵阳 621900)

3)(北京大学,应用物理与技术中心,北京 100871)

4)(上海交通大学,聚变科学与应用协同创新中心,上海 200240)

1 引 言

激光间接驱动惯性约束聚变(ICF)的原理是:将激光束入射到一个内装靶丸的高Z元素构成的黑腔内壁上,内壁吸收激光能量并以很大的份额转换为X射线,然后通过输运使黑腔内部的X射线尽可能均匀烧蚀靶丸表面,驱动靶丸实现球形内爆,进而聚变点火、燃烧放能[1].因此,间接驱动研究中的一项重要课题是黑腔辐射场研究.对于靶丸内爆而言,理想的条件是黑腔能够提供温度足够高且分布均匀的辐射场,因此,设计出激光-X光耦合效率足够高、均匀性足够好的黑腔是黑腔研究及激光聚变研究的重点之一[2,3].

间接驱动惯性约束聚变概念提出至今已有四十多年,其间美国主要致力于柱型黑腔的理论与实验研究[3].为开展激光聚变研究,美国建造了迄今世界上最大的激光装置——国家点火装置(NIF)[4],当时计划于2012年实现点火,但实验未能获得成功[5],其中一个重要原因是柱腔中难以获得足够均匀的辐射场[6].近年,我国ICF黑腔团队提出一种六孔球型黑腔并开展了系统的理论研究,给出了六孔球腔的概念、设计、创新构型和皮实度分析[7−11].初步理论研究表明,六孔球腔具有高辐照均匀度优势,在无需任何辅助技术手段的情况下,该型黑腔拥有全维度高辐照均匀度、高能量耦合效率、高皮实度三大特性[12].

六孔球腔具有显著的三维特性,因此需要三维程序才能开展合适的数值模拟研究.近年,我国研究人员发展了基于隐式蒙特卡罗(implicit Monte Carlo,IMC)方法[13]的三维辐射输运数值模拟程序IMC3D[14],目前可以初步应用于黑腔物理研究.六孔球腔的实验尚未开展,但先期已在我国的神光系列激光装置上开展了一些两孔球型黑腔的相关实验[15].本文针对2015年在神光III激光装置上实施的一次实验开展数值模拟研究,比对分析数值模拟结果与实验结果,检验黑腔辐射场数值模拟能力.

2 两孔球型黑腔实验概述

神光III上两孔球腔如图1(a)所示.黑腔形状为球形,半径1.8 mm,腔壁材料为金,壁厚50µm.黑腔上下端(北极、南极)开有激光注入孔(LEH),孔半径0.6 mm,激光由两个LEH分别注入并在腔内壁形成若干光斑,光斑在腔内壁的分布(纵剖面图)如图1(b)所示.实验中共有32路(上24下8)激光在3 ns时间范围内均匀注入,激光总能量86.4 kJ.黑腔中心分为两种情况:布置靶丸和不布置靶丸.靶丸为半径0.48 mm的CH小球.黑腔放置在半径为3 m的球形靶室中心,靶室上布置若干平板响应式X射线探测器( fl at response X-ray detector,FXRD),如图1(c)中蓝点所示.

图1 (a)激光注入黑腔示意图;(b)光斑分布示意图;(c)FXRD位置示意图Fig.1.(a)Laser beams in hohlraum;(b)spots on the wall of hohlraum;(c)locations of FXRDs.

3 数值模拟方法与程序

两孔球腔的结构为二维旋转对称,但是考虑激光光斑的分布时,辐射场分布将不具备二维旋转对称性,用三维结构来描述整个系统才更加合理.本文利用三维辐射输运数值模拟程序IMC3D进行模拟.IMC3D采用隐式蒙特卡罗方法求解辐射输运问题.单一离散时间步[tn,tn+1]内,求解如下IMC辐射输运方程[14]及物质温度方程:

式中I=chνn(r,Ω,ν,t)为辐射强度,n(r,Ω,ν,t)为相空间(r,Ω,ν,t)的光子数密度,c为光速,h为普朗克常数,r为光子位置,Ω为光子飞行方向,ν为光子频率,t为时间;其他所有带有下标n的物理量均表示离散时间步[tn,tn+1]起始时刻tn(或初始时刻t0)的物理量,且均为已知量:Tn为物质温度,bn为归一辐射普朗克函数,Qn为独立辐射外源,cv,n为物质比热,fn为 fl eck因子,σa,n为吸收不透明度系数,σea,n=fnσa,n为有效吸收系数,σea,n=(1−fn)σa,n为有效散射系数,σp,n为普朗克平均吸收截面,Ur,n为辐射能量密度,ζn为局域再发射谱.(1)式和(2)式中辐射强度I和物质温度Tn+1为待求未知变量.

对两孔球腔问题进行模拟的步骤如下:

1)对球腔作空间离散,制成三维网格模型,作时间离散;

2)按离散时间步,将与时间相关的激光能量分别加在腔壁光斑区对应网格上,求解能量(温度)方程,得到网格温度(升高),各网格按照温度及发射(吸收)系数产生相应的辐射光子源(Planck谱);

3)利用蒙特卡罗方法模拟跟踪光子输运过程,包括飞行、碰撞吸收、散射等物理过程;

4)统计计数光子能量沉积(交给物质)、现存及漏失光子的能谱和角度谱分布等,并按照能量方程计算新的物质温度,开始下一离散时间步计算;

5)完成所有离散时间步计算后,根据统计计数结果处理其他物理量,如黑腔、激光注入孔平均辐射温度,靶丸表面辐射流等效温度,靶室内表面等效辐射温度,探测器等效辐射温度等.

黑腔平均辐射温度计算公式为

式中a为辐射常数,V为黑腔体积,Er,H为黑腔现存光子总能量.如果Er,H为黑腔中某网格的现存光子总能量,V为黑腔中某网格的体积,则计算得到该网格体的平均温度.

LEH平均辐射温度为

式中c为光速,Δt为时间步长,SLEH为LEH面积,Er,L为当前时间步从LEH漏失的光子能量.

靶丸表面辐射流等效温度为

式中SCap为靶丸表面积,Er,C为当前时间步从靶丸外表面流入、流出的光子能量.

FXRD等效辐射温度为

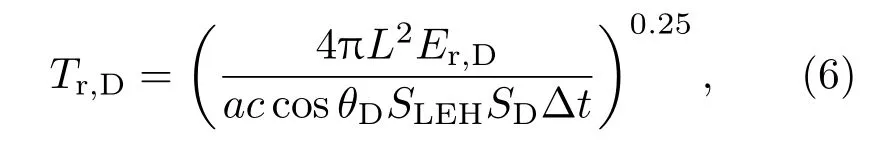
式中SD为FXRD探头面积(接收光子面积),θD为FXRD探头瞄准方向与LEH外法向夹角,L为FXRD与LEH之间的距离,Er,D为当前时间步进入FXRD的光子能量.(6)式中将FXRD处的实际辐射温度与LEH处的平均辐射温度进行了可比等效转换.

4 数值模拟结果及与实验结果的对比

利用IMC3D辐射输运程序模拟两孔球腔实验,由于IMC3D程序目前暂时未实现与流体程序的耦合,因此激光能量只能转化成辐射能和物质的内能两部分.然而实际过程中有一部分(约25%)激光能量会转化为物质的动能,另外还有约5%的背反激光能量损失.将这两个因素考虑在内,因而在实际模拟过程中将加在网格上的激光能量减小了30%.下面分别给出带靶丸模型和不带靶丸模型的数值模拟结果并作定性分析,同时将模拟结果与实验结果进行比较.

对于带靶丸的模型,至激光注入结束时刻(3 ns时刻),由IMC3D模拟得到的能量分配情况如下:注入激光能量为3.2×1017MeV,物质内能为2.549×1017MeV,现存辐射能为5.482×1017MeV,总漏失辐射能为5.959×1017MeV.

激光能量大约有20%转化为辐射能,其他约80%被物质吸收后转化为物质内能.另外,从计算结果可知,至3 ns时刻,靶丸净吸收能量为4.18×1016MeV,约占注入激光总能量的13%,这与已有的认知基本一致.

图2(a)所示为黑腔、注入孔辐射温度及靶丸入流、出流等效辐射温度随时间的演化情况,黑腔平均辐射温度在3 ns时刻达到最高值,为230 eV.图2(b)所示为靶丸表面出射辐射流与入射辐射流之比(反照率)随时间的演化情况.图3所示为3和4 ns时刻的黑腔辐射温度场(纵剖面).从图2和图3可以看出,在激光注入阶段,黑腔温度与靶丸入流温度基本一致,靶丸出流温度低于黑腔温度,原因在于开始阶段靶丸温度较低,进入靶丸的辐射能被CH材料吸收后主要转化为物质内能,靶丸向外辐射的能量低于吸收能量;同时,靶丸质量较大,需要加热的时间较长,到3 ns时物质温度与辐射温度未能达到平衡,入射辐射流大于出射辐射流(反照率约为0.83).激光停止注入后,黑腔温度先有短暂的快速下降过程,然后下降速度减缓,靶丸出流温度高于黑腔温度及入流温度,原因在于金壁被激光加热的质量较小,且其吸收发射能力很强,在没有激光源的情况下很快与黑腔辐射场达到平衡,而黑腔有开口,辐射温度快速下降使得金壁温度也下降较快,当温度下降到低于靶丸物质温度后,靶丸成为辐射源的净提供体,出射辐射流大于入射辐射流(反照率超过1.0),而靶丸被加热的质量较大且吸收发射能力比金弱得多,因此黑腔辐射温度缓慢降低.整个过程中注入口等效温度略低于黑腔平均温度,原因在于注入口不是X光转换区,而是黑腔辐射场的壑,从图3可清楚看到.另外,图3(a)中的部分腔壁及附近温度明显更高,原因是该腔壁位置存在激光光斑;图3(b)中由于激光注入已经结束,腔壁温度十分均匀.

图2 (a)黑腔、注入孔及靶丸表面出入流辐射温度时间演化;(b)靶丸反照率时间演化Fig.2.(a)Temporal evolution of average radiation temperatures of hohlraum,LEH,and capsule;(b)temporal evolution of capsule re fl ection ratio.

图3 (a)黑腔辐射温度场分布(3 ns时刻);(b)黑腔辐射温度场分布(4 ns时刻)Fig.3. (a)Radiation temperature distribution of hohlraum at 3 ns;(b)radiation temperature distribution of hohlraum at 4 ns.

图4 辐射温度随时间的变化 (a)上0°;(b)上16°;(c)上42°;(d)下20°Fig.4.Radiation temperature versus time:(a)Up 0°;(b)up 16°;(c)up 42°;(d)down 20°.

图4所示为从激光注入口外4个角度观测到的腔内辐射温度随时间演化的模拟与实验结果的对比.图中黑色实线为数值模拟结果,红色实线为实验中FXRD探测到的结果.图4(a)为探测器布置在上部且与LEH外法向夹角为0°(正对上部LEH)时的结果.图4(b)和图4(c)分别为探测器与上LEH外法向夹角为16°,42°的结果,图4(d)是探测器与下LEH外法向夹角为20°的结果.从图中结果可以看出:数值模拟结果与实验结果总体上比较接近,其中0°角方向的结果差别较大,其他三个方向的结果较为符合.造成0°角辐射温度的差异,尤其是温度较低阶段(0—1.5 ns),初步分析主要原因如下.数值模拟没有考虑流体运动,故上0°角FXRD所能接收的辐射光子主要由两部分组成,一部分由中心靶丸发射,另一部分由下腔口附近腔壁发射.但是在实际情况中,除了这两部分之外,还有腔壁(尤其是光斑区)向腔内喷射的稀薄金等离子体所发射的光子.在靶丸温度上升之前(1.5 ns时刻),喷射入腔内的金等离子体可能起主导作用,但当靶丸温度足够高后,靶丸辐射光子占主导地位.对于其他3个角度方向,FXRD能接收的辐射光子绝大部分来自腔壁,喷射入腔内的金等离子体发射光子所占份额较小,而且金等离子体还对腔壁光子存在一定的阻挡、弥散作用,因此数值模拟结果略小于实验结果,但总体符合较好.

对于不带靶丸的模型,至激光注入结束时刻(3 ns时刻),由IMC3D模拟得到的能量分配情况如下:注入激光能量为3.2×1017MeV,物质内能为2.397×1017MeV,现存辐射能为6.414×1015MeV,总漏失辐射能为7.390×1016MeV.与带靶丸模型的计算结果相比,转化为辐射能的激光能量多5%,转化为物质内能的激光能量少5%.

图5所示为不带靶丸和带靶丸的黑腔辐射温度、LEH辐射温度比较,不带靶丸的黑腔平均辐射温度在3 ns时刻达到最高值,为238 eV,略高于带靶丸情况下的计算结果(230 eV).这是因为没有靶丸吸能,更多的激光能量转化为辐射能.图6所示为3和4 ns时刻的黑腔辐射温度场(纵剖面),可以看出除光斑区和注入口附近外,黑腔辐射场比较均匀.

图5 黑腔和激光注入孔辐射温度比较Fig.5.Temporal distributions of average radiation temperatures of hohlraum and LEH.

图7所示为不带靶丸情况下FXRD处辐射温度随时间的演化.与带靶丸情况相似,0°角方向的结果差别较大,其他三个方向的结果符合较好.0°角方向的差异(尤其是后期)比带靶丸情况更大,这是因为数值模拟没有考虑喷射入腔内的金等离子体对FXRD的辐射贡献,对于不带靶丸的情况,数值模拟中进入0°角FXRD的只有下腔口附近腔壁发射的光子,由于没有在后期起主导作用的靶丸辐射光子,因此忽略喷射入腔内的金等离子体辐射光子的贡献而引入的相对误差必然更大.

图7 辐射温度随时间的变化 (a)上0°;(b)上16°;(c)上42°;(d)下20°Fig.7.(a)Radiation temperature versus time:(a)Up 0°;(b)up 16°;(c)up 42°;(d)down 20°.

图8所示为带靶丸和不带靶丸两种情况下0°角FXRD辐射温度的比较.在大部分时间范围内,带靶丸时辐射温度比不带靶丸时高得多,这是靶丸辐射光子进入FXRD所致.但是,在前期(0—1.2 ns)不带靶丸的辐射温度更高,原因在于靶丸对0°角FXRD的辐射流(温度)贡献可以分为两部分(图9),其一为正作用,靶丸上半部辐射的光子进入FXRD,其二为负作用,靶丸阻挡下腔口附近腔壁辐射的光子进入FXRD.在靶丸温度上升之前(约1.2 ns时刻),靶丸发射光子能力弱,吸收光子能力强,故以负作用为主,计算得到的带靶丸情况下FXRD温度低于不带靶丸情况;之后,靶丸上半部辐射的光子贡献大于其阻挡作用,且随着靶丸温度的上升FXRD温度差距愈加显著.

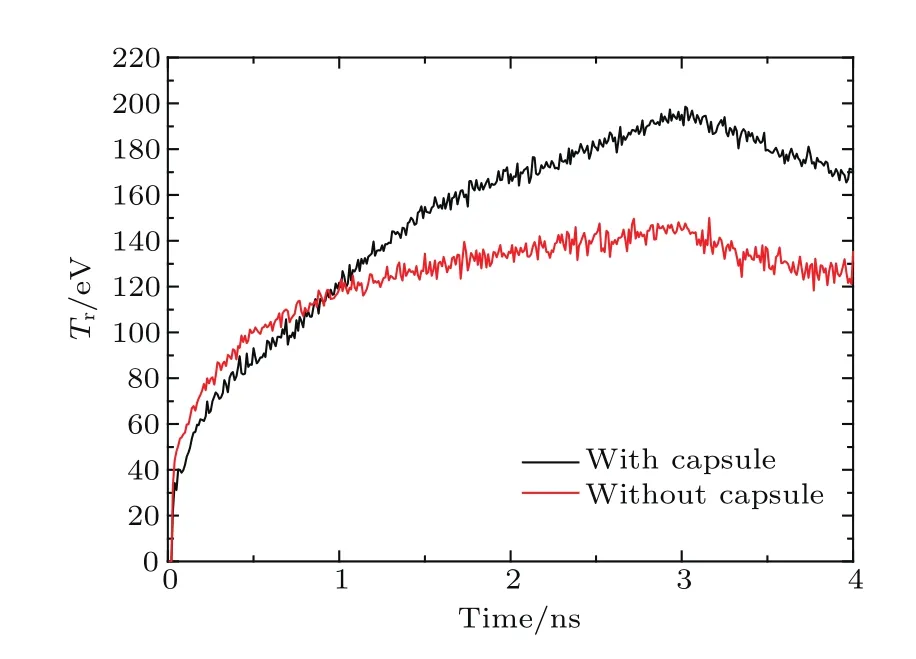
图8 FXRD辐射温度比较(上0°)Fig.8.Temporal distribution of calculated FXRD radiation temperature for up 0°.

图9 黑腔、靶丸与0°角FXRD位置示意图Fig.9.Location of hohlraum,capsule and FXRD for up 0°.

5 结 论

利用三维IMC辐射输运数值模拟程序模拟神光III实验中两孔球腔辐射场,模拟结果与实验结果进行比较发现:带靶丸的黑腔平均辐射温度最高可达230 eV,靶丸吸能效率约为13%;不带靶丸的黑腔平均辐射温度最高可达238 eV.在激光加源时段,靶丸表面入射辐射流高于出射辐射流,靶丸反照率逐渐上升至0.83左右;激光加源结束后,靶丸表面出射辐射流高于入射辐射流,靶丸反照率大于1.0,是辐射源的主要供体.在靶丸温度上升之前,带靶丸情况下0°角方向的FXRD辐射温度低于不带靶丸的情况,但在靶丸温度上升之后,带靶丸情况下0°角方向的FXRD辐射温度远高于不带靶丸的情况.FXRD处辐射温度随时间的演化与实验结果总体上较为一致,其中处于16°,20°和42°三个方位的结果与实验结果符合较好,而处于0°角方位的结果与实验结果差异较大,这可能是模拟中未能考虑腔壁(主要是光斑区)向腔内喷射稀薄金等离子体的影响所致.综合数值模拟结果及其与实验结果的对比可知,IMC3D程序具备较好的黑腔三维辐射输运数值模拟能力,能够给出较为丰富的物理量,尤其是能够灵活方便地得出实验诊断类物理量,模拟结果基本可靠.下一步需要开展的主要工作是与三维辐射流体力学数值模拟程序相耦合,更加真实、全面地模拟黑腔辐射场的动态演化过程;还要继续开展计算方法研究,进一步扩大模拟样本规模,提高数值模拟精度以增强六孔球腔三维数值模拟置信度,为黑腔理论研究及实验设计提供参考.

[1]Zhang J,Chang T Q 2004Fundaments of the Target Physics for Laser Fusion(Beijing:National Defense Industry Press)(in Chinese)[张均,常铁强 2004激光核聚变靶物理基础(北京:国防工业出版社)]

[2]Atzeni S,Meyer-ter-Vehn J(Shen B F,Transl.)2008The Physics of Inertial Fusion(Beijing:Science Press)(in Chinese)[阿蔡塞,迈耶特费 (沈百飞 译)2008惯性聚变物理(北京:科学出版社)]

[3]Lindl J D 1995Phys.Plasmas2 3933

[4]Moses E I,Boyd R N,Remington B A,Keane C J,Al-Ayat R 2009Phys.Plasmas16 041006

[5]Moses E I,Lindl J D,Spaeth M L,Patterson R W,Sawicki R H,Atherton L J,Baisden P A,Lagin L J,Larson D W,Magowan B J,Miller G H,Rardin D C,Roberts V S,van Wonterghem B M,Wegner P J 2016Fusion Sci.Technol.69 1

[6]Lindl J D 2014Phys.Plasmas21 020501

[7]Lan K,Liu J,Lai D X,Zheng W D,He X T 2014Phys.Plasmas21 010704

[8]Lan K,He X T,Liu J,Zheng W D,Lai D X 2014Phys.Plasmas21 052704

[9]Lan K,Zheng W D 2014Phys.Plasmas21 090704

[10]Huo W Y,Liu J,Zhao Y Q,Zheng W D,Lan K 2014Phys.Plasmas21 114503

[11]Li S,Lan K,Liu J 2015Laser Part.Beams15 263

[12]Lan K,Liu J,Li Z C,Xie X F,Huo W Y,Chen Y H,Ren G L,Zheng C Y,Yang D,Li S W,Yang Z W,Guo L,Li S,Zhang M Y,Han X Y,Zhai C L,Hou L F,Li Y K,Deng K L,Yuan Z,Zhan X Y,Wang F,Yuan G H,Zhang H J,Jiang B B,Huang L Z,Zhang W,Du K,Zhao R C,Li P,Wang W,Su J Q,Deng X W,Hu D X,Zhou W,Jia H T,Ding Y K,Zheng W G,He X T 2016Matter Radiat.Extremes1 8

[13]Fleck J A,Cummings J D 1971J.Comput.Phys.8 313

[14]Li S,Li G,Tian D F,Deng L 2013Acta Phys.Sin.62 249501(in Chinese)[李树,李刚,田东风,邓力 2013物理学报62 249501]

[15]Huo W Y,Li Z C,Yang D,Lan K,Liu J,Ren G L,Li S W,Yang Z W,Guo L,Hou L F,Xie X F,Li Y K,Deng K L,Yuan Z,Zhan X Y,Yuan G H,Zhang H J,Jiang B B,Huang L Z,Du K,Zhao R C,Li P,Wang W,Su J Q,Ding Y K,He X T,Zhang W Y 2016Matter Radiat.Extremes1 2